提高工件表面缺陷提取鲁棒性的改进低秩矩阵恢复算法

张晶 刘丽冰 黄智坤 袁军 杨泽青

摘要 针对传统的工件缺陷提取方法存在鲁棒性差的问题，提出一种基于同态滤波的改进低秩矩阵恢复算法。首先使用同态滤波方法增强光照分量、抑制工件反射分量，减小光照不均和工件强反光产生伪缺陷的影响；然后应用鲁棒主成分分析模型将工件表面缺陷提取问题转换为低秩背景矩阵和稀疏缺陷矩阵分离的低秩矩阵恢复问题；最后使用非精确拉格朗日乘子法对由鲁棒主成分分析模型转化的凸优化模型进行求解。以带有凹坑、划痕缺陷的轴类工件为样本，通过计算F-measure值完成方法验证，实验结果表明：在不同光照强度的实验条件下，离散傅里叶算法提取凹坑缺陷和划痕缺陷的平均F值分别为0.435 7和0.381 9；本文提出算法提取凹坑缺陷和划痕缺陷的平均F值分别为0.726 0和 0.716 9，结果验证了所提算法的有效性和较高鲁棒性。

关 键 词 缺陷提取；低秩矩阵恢复；同态滤波；非精确拉格朗日乘子法；鲁棒性

中图分类号 TH164     文献标志码 A

Improved low-rank matrix restoration algorithm for improving the robustness of workpiece surface defect extraction

ZHANG Jing， LIU Libing， HUANG Zhikun， YUAN Jun， YANG Zeqing

（School of Mechanical Engineering， Hebei University of Technology， Tianjin 300401， China ）

Abstract An improved low rank matrix recovery algorithm based on homomorphic filtering was proposed to solve the problem of poor robustness in the traditional methods of extracting workpiece defects. Firstly， the homomorphic filtering method was used to enhance the illumination component and suppress the reflection component of the workpiece to reduce the influence of illumination unevenness and strong reflection of the workpiece to produce false defects. Then the robust principal component analysis model was used to transform the surface defect extraction problem into the low-rank matrix recovery problem separated from the low-rank background matrix and the sparse defect matrix. Finally， an imprecise Lagrangian multiplier method was used to solve the convex optimization model transformed from the robust principal component analysis model. With indentation， scratch defects such as axial workpiece as sample， by calculating the F-measure values completion methods validation， the experimental results show that under the condition of different light intensity experiment， the average F value of pit defect and scratch defect extracted by Discrete fourier transform is 0.435 7 and 0.381 9; in this paper， the average F value of pit defect and scratch defect extracted by the algorithm is 0.726 0 and 0.716 9， the results show that the proposed algorithm is efficient and robust.

Key words defect extraction; low rank matrix recovery; homomorphic filtering; imprecise lagrangian multiplier method; robustness

0 引言

工件表面缺陷檢测是工业生产中的一个重要环节，对减少资源浪费、保证后续加工和使用的安全性、提高产品合格率具有极大价值[1-3]。工件表面缺陷提取是缺陷检测的基础，去除背景纹理、减小噪声和光照不均等因素的影响，恢复缺陷的真实信息是十分重要的。

目前缺陷提取算法主要分为基于空间域提取和基于频域提取两类。1）空间域提取算法主要包括阈值分割、边缘检测和模糊聚类等方法，利用缺陷区域的灰度、边缘、纹理等特征信息，实现缺陷的提取。张静等[4]针对金属工件表面存在光照不均的问题，提出局部二元模式与局部图像方差强度结合的方法，处理后的缺陷图像仍存在较多噪声点。任盛伟等[5]提出一种鲁棒实时的钢轨表面擦伤检测算法，实现图像的增强，车辆过弯检测效果不佳。陈顺等[6]针对含噪齿轮图像边缘检测存在噪声的问题，提出Canny算子和数学形态学融合算法去噪，但是图像的部分真实边缘未被检测出来。2）频域提取算法主要包括离散傅立叶变换、小波变换等方法，将图像变换到频域，根据缺陷与背景区域的频率差使用滤波器滤除背景，再通过逆变换实现缺陷提取。Ang Wu等[7]针对薄膜晶体管表面的微缺陷检测的问题，应用离散傅里叶变换去除背景纹理，小波变换消除光照不均影响。由以上分析可知，传统的缺陷提取方法受噪声、光照不均的影响较大，工件材料自身的反光或曲面特性，使获得的图像表面光强度不一致，经常将中心亮区的边界误认为缺陷[8]；缺陷目标在整个图像中所占的像元很少，且信噪比低 [2]等问题，使得工件表面缺陷提取的鲁棒性不高。

近年来，低秩矩阵恢复算法被广泛应用在图像处理、信号处理、计算机视觉、高维数据分析等各个领域。应用低秩矩阵恢复算法实现微裂纹[9]、织物疵点[10]、TFT-LCD表面缺陷[11]、红外图像小目标[12]、人脸图像[13]、太阳能电池片[14]的检测或识别，具有较好的噪声抑制效果。本文首次提出将低秩矩阵恢复算法应用到工件表面缺陷提取，考虑金属工件存在的光照不均问题，提出改进的低秩矩阵恢复算法。首先应用同态滤波算法平衡光照，然后应用低秩矩阵恢复算法进行背景纹理和缺陷的分离，实现工件表面缺陷提取鲁棒性的提高。

1 工件表面缺陷提取算法及其鲁棒性分析

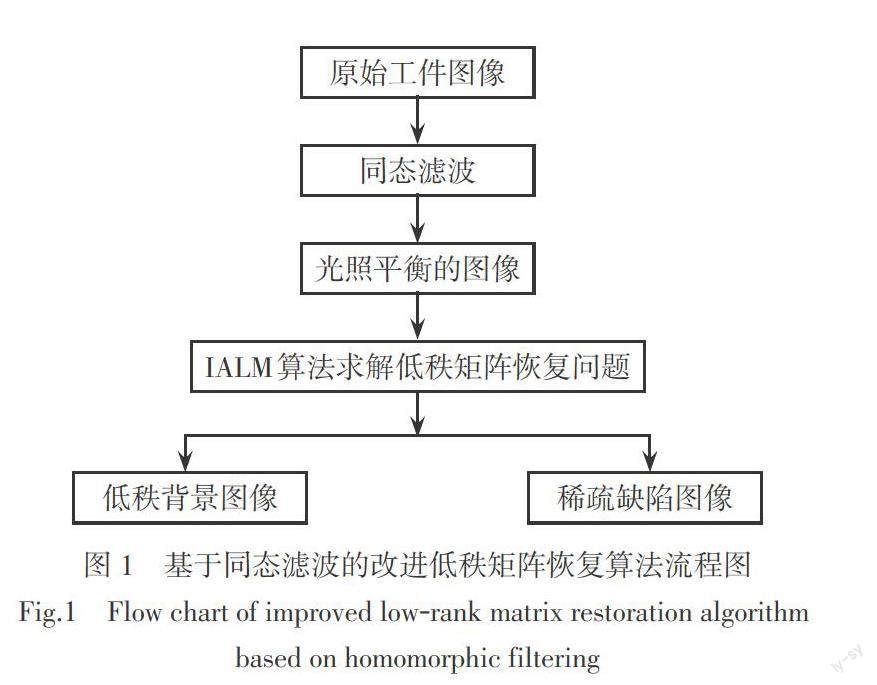
目前工件缺陷提取研究大多是在特定的光照环境下采集工件表面图像，但是在实际的生产加工中，环境变化对图像采集质量的影响难以忽略，光照变化会使得传统的缺陷提取算法的准确率和鲁棒性下降，造成缺陷的误检和漏检，因此需要研究一种可以在不同光照条件下都有较高鲁棒性的缺陷提取算法，提高复杂环境下缺陷提取的准确率。本文提出算法流程如图1。

低秩矩阵恢复算法可以在矩阵中某些元素被破坏时，自动识别出被破坏的元素并且恢复出原矩阵，因此被广泛应用在缺陷检测、人脸识别和图像重建中，应用低秩矩阵恢复算法进行工件表面缺陷提取时，可将有缺陷的图像分为无缺陷背景纹理区和缺陷前景区2部分，分别用低秩矩阵和稀疏矩阵表示，同时考虑光照变化的影响，本文将同态滤波算法与低秩矩阵恢复算法相结合，研究了一种具有较高鲁棒性的工件缺陷提取算法。

2 改進的低秩矩阵恢复算法研究

现今，减小光照对工件表面缺陷提取的影响，根据应用的算法技术的不同，主要可以分为基于二维图像光照预处理方法和基于三维模型方法，三维模型方法是将光照作为独立变量来建立模型，生成任意光照下的工件表面图像，来达到消除光照变化的影响，但是基于三维模型的方法需要大量不同光照下的训练样本，难以满足现今工件表面缺陷提取的实时性，所以本文主要讨论基于二维图像的光照处理上。光照预处理解决工件表面光强不均匀问题，常用的解决方法有：全局直方图均衡、梯度增强法、基于离散小波变换的同态滤波、多尺度Retinex、动态均质补偿等，考虑运算速度、资源节约和对高光、反光区域的处理效果等方面，应用基于照明-反射模型的同态滤波算法进行光照处理。

2.1 同态滤波算法

由于工件的自身材质和形状影响，金属工件表面光滑、阶梯轴类工件的阶梯处容易出现反光，采集到的图像存在着强反光的问题。

在照明-反射光照模型中，可看作由照射分量与反射分量所组成，即原始图像[I（x，y）]可以表示为光的照射分量[m（x，y）]和工件的反射分量[n（x，y）]的乘积[15]，如式（1）所示：

式中：由于光照是渐变的，照射分量[m（x，y）]频谱集中在低频段；由于工件表面的光照反射是非渐变的，反射分量[n（x，y）]频谱集中在高频段。

基于照明-反射模型的同态滤波的处理过程如下。

输入 [I（x，y）] ，输出 [Ip（x，y）] 。

步骤1：[Ix，y=mx，y?nx，y]两边取对数，然后做傅里叶变换得到线性组合的频域形式：

步骤2：应用传递函数[H（x，y）]对数据进行滤波处理，然后做傅里叶逆变换和数据的指数变换，得到处理后的图像为[IPx，y]。

同态滤波算法是通过传递函数来处理照射分量和反射分量的，传递函数的选择是获得高质量图像的关键，同态滤波传递函数是基于高通滤波器函数修改得到，常用的高通滤波器有高斯滤波器和巴特沃斯高通滤波器。

基于高斯滤波器的同态滤波传递函数如式（3）：

基于巴特沃思高通滤波器的同态滤波传递函数如式（4）：

式中：[D0]为截止半径；[rH]为高频增加倍数；[rL]为低频缩小倍数；常数[c>0]，用于调节函数形状；[n]为滤波器阶数。

基于照明-反射模型的同态滤波是在高通滤波器的截止半径[D0]的基础上放大[rH，rL]倍，高频增加[rH]倍[rH>1]，低频缩小[rL]倍[rL<1]，通过增强光照的高频分量、抑制工件反射的低频分量，达到增加图像对比度、减小强反光影响的目的。因此可以较好地保留图像细节，提高缺陷提取的光照鲁棒性，减少光照不均产生的伪缺陷，降低缺陷误检率。

2.2 低秩矩阵恢复算法

低秩矩阵恢复又称为鲁棒主成分分析（Robust Principal Component Analysis，RPCA）或低秩稀疏分解。低秩矩阵恢复主要由鲁棒主成分分析、矩阵补全和低秩表示等3类模型组成[16]，当矩阵中的所有元素都能观测到，则适用与鲁棒主成分分析模型。RPCA原理可以从PCA（Principal Component Analysis）的角度看。PCA作为对高维数据有效降维的方法之一，将高维数据在低维线性子空间上投影，即可以保留原有特征的主要信息，又可以减小特征的个数，可以表示为式（5）：

通过上述约束优化寻找最近的线性子空间的投影。当高斯噪声[E]较小时，PCA可以通过一次奇异值分解准确找到最优原始数据矩阵[A]，当[E]较大时，[A]的估计往往不准确。由于其不适用于稀疏的大噪声矩阵，当面对较大噪声干扰时不能很好的完成降维任务，所以Wight等[17]提出RPCA模型，将原始数据矩阵[D]定义为由低秩部分[A]和稀疏噪声部分[E]组成，可以用式（6）表示：

式中：目标函数是低秩矩阵[A]的秩和稀疏矩阵[E]的零范数；[λ]表示噪声所占的权重；[D]的每一列是给定已知的数据。

由于这是一个非确定多项式难题，在理论和实践中，均存在指数复杂度（相对于矩阵维数n）的算法，而没有有效的算法。随着鲁棒主成分分析模型的广泛使用，越来越多的解决鲁棒主成分分析模型的方法被提出，这些方法一般可被分为3类：基于凸优化模型的方法、基于贝叶斯理论的方法和基于M估计的方法[18]。应用比较广泛的是凸优化模型方法，通过对目标函数进行松弛，将原先的非凸的零范数替换为更容易处理的稀疏性度量函数，从而转换为如下凸优化问题进行求解：

式中：[A?=i=1mδi（A）]，表示矩阵[A]的第[i]个奇异值；[E1=ijEij]；表示矩阵[E]所有元素的绝对值之和。

将RPCA模型应用到工件表面缺陷检测中，由背景纹理的特性可知，背景纹理属于周期性纹理，表示在图像矩阵中是线性相关的，即可以表示为低秩矩阵；由于稀疏性定义为目标区域面积占很小的比重或者检测目标的个数占很小的比重，存在的缺陷可以理解为稀疏矩阵中的非零元素，即可以将缺陷表示为稀疏矩阵。从而将工件表面缺陷提取问题转化为低秩矩阵恢复问题进行求解，将同态滤波处理后的均匀光照图像，分解为无缺陷低秩背景图像和有缺陷稀疏缺陷图像。

2.3 凸优化模型求解方法

通过转化后的凸优化问题来逼近求解原问题，在工件表面缺陷检测的背景下，有效地的求解凸优化模型是一个待解决的关键问题。求解凸优化模型的常用方法有增广的拉格朗日乘子法、加速的近端梯度法、迭代阈值法和近端梯度法等。综合考量考虑图像矩阵维数、精确度、方法收敛速度和迭代次数等，因非精确拉格朗日乘子法（Inexact Augmented Lagrange Multiplier，IALM）有更好的精确度、较少迭代次数和收敛率，近年来被广泛研究使用。

本文利用IALM来求解，构造凸优化问题的拉格朗日函数

式中：[Y]为拉格朗日乘子；[μ]是惩罚参数，[μ>0]；[λ]为权重因子。

可以先固定一个[Y]和[E]求得一个[L]使[A]最小，然后固定一个[Y]和[A]求得一个[L]使[E]最小，依此交替更新迭代，最终得到一个收敛到这个子问题的最优解，这个算法称为精确拉格朗日乘子法。但是在工件表面缺陷检测中，考虑图像处理需要满足在线、实时性等问题，只需每次迭代更新获得[A]和[E]近似解，这样就会以最快收敛速度方式得到收敛得到原问题的最优解，即非精确拉格朗日乘子法，其求解凸优化问题的流程图如图2所示。

图2中，[D∈Rm×n]为同态滤波处理后的图像矩阵，初始化参数[Y0=DJ（D）;E0=0;][μ0>0;][ρ>1;][k=0]，[JD=maxD2，λ-1D∞]，[Sεx]为软阈值操作，公式如下：

使用IALM时，惩罚参数[μ]、终止迭代参数[δ]、最大迭代次数[θ]会直接影响缺陷提取的效果，参考文献[14]和实验验证，[μ=n1n24D1]，其中[n1]和[n2]是输入矩阵的[D]的行數和列数，本文输入图片矩阵为[1 200×960]；当[D-A-EF≤δDF]，当[δ=10-7]时停止迭代；[θ=1 000]。

3 实验结果与分析

3.1 实验描述

为了验证和评估改进低秩矩阵恢复算法的有效性，本文使用天津某机械厂生产的轴类工件（最大轴径为15 mm、长为15 mm）进行测试，测试样本分为划痕缺陷样本和凹坑缺陷样本两类，配合型号为MV-BL100X100-V的白色面光源，调节光源适配器光强旋钮，在图像采集时进行不同光强度处理。实验测试图像库共300幅，其中，旋钮调至5级时的缺陷图像100幅，旋钮调至3级时的缺陷图像100幅，旋钮调至1级的缺陷图像100幅。本文实验平台是4核CPU，主频1.4 GHz，8 GB内存，Intel Core i5系统的笔记本电脑，应用的仿真环境是MATLAB R2019b。实验结果和分析共包括2部分内容：1）基于照明-反射模型的同态滤波算法的处理效果；2）传统缺陷提取算法（离散傅里叶变换算法）和基于同态滤波的改进低秩矩阵恢复算法的结果比较。

3.2 工件图像的同态滤波处理结果

图3为3种不同光照强度下的工件图像，利用基于照明-反射模型的同态滤波算法进行处理，以减小反光现象的影响。旋钮调至5级时，工件的高频反射分量较大，实验验证当同态滤波的传递函数中截止半径[D0=5]，[rH=2.5]，[rL=0.2]，[c=1]时，图像效果最佳；当旋钮调至3级时，同态滤波函数的截止半径[D0=10]，[rH=1.8]，[rL=0.3]，[c=1]效果最好；当旋钮调至1级时，同态滤波函数的截止半径[D0=15]，[rH=1.3]，[rL=0.4]，[c=1]效果最佳。处理效果如图4所示。

同态滤波算法处理不同光强下的图像，实验证明该算法可以削弱工件表面强反光影响，使工件表面缺陷提取在光照问题上有较好的鲁棒性，为之后的缺陷提取打下良好的基础。

3.3 工件表面缺陷提取算法的对比

为验证本文提出算法在鲁棒性方面的提升，选择应用比较广泛的离散傅立叶变换进行实验对比，并采用F-measure值来定量评估2种算法，F-measure值为一种综合性能评价指标，取值介于[0，1]，F值的定义为式（10）：

式中：[r=PT（PT+NF）]为召回率；[p=PT（PT+PF）]为准确率；[PT]为被正确判断为缺陷的像素个数；[PF]为被误判为缺陷的像素数目；[NF]为被误判为背景的缺陷像素数目，F值越高表明该算法对工件表明缺陷提取的效果越好。

由表1可以看出，传统的缺陷提取算法受光照影响较大，提取凹坑缺陷的平均F值为0.435 7，提取划痕缺陷的平均F值为0.381 9；本文提出的算法在不同光照强度下，可以保持在一个相对较高检测的水平，提取凹坑缺陷的平均F值为0.726 0，提取划痕缺陷的平均F值为0.716 9，说明本文提出算法相比传统方法提高了缺陷提取鲁棒性。

4 结语

研究了一种基于同态滤波的改进低秩矩阵恢复算法，分析了同态滤波的传递函数平衡光照分量和工件反射分量的机理，确定了同态滤波传函的截止半径，实现了不同光强条件下的工件表面光照平衡。然后对同态滤波处理后的图像使用低秩矩阵恢复算法，再使用非精确拉格朗日乘子法求解由鲁棒主成分分析模型转化的凸优化模型，得到分离的低秩背景图像和稀疏缺陷图像。最后通过F-measure值来定量评估本文提出的算法性能，结果表明该算法在轴类工件缺陷提取具有有效性和较高的鲁棒性。

参考文献：

[1]    YANG J X，FU G Z，ZHU W B，et al. A deep learning-based surface defect inspection system using multiscale and channel-compressed features[J]. IEEE Transactions on Instrumentation and Measurement，2020，69（10）：8032-8042.

[2]    赵君爱，贾民平. 工件表面微小缺陷的检测与识别方法[J]. 东南大学学报（自然科学版），2014，44（4）：735-739.

[3]    赵俊忠，黄厚宽，贾莲凤. 误差分离理论在微机辅助轴类工件表面缺陷检测中的应用[J]. 计量学报，2003（1）：14-17.

[4]    张静，叶玉堂，谢煜，等. 金属圆柱工件缺陷的光电检测[J]. 光学 精密工程，2014，22（7）：1871-1876.

[5]    任盛伟，李清勇，许贵阳，等. 鲁棒实时钢轨表面擦伤检测算法研究[J]. 中国铁道科学，2011，32（1）：25-29.

[6]    陈顺，李登峰. 融合Canny算子和形态学的齿轮图像边缘检测研究[J]. 机电工程，2020，37（7）：821-825.

[7]    WU A，ZHU J H，TAO Z L，et al. Automatic inspection and classification for thin-film transistor liquid crystal display surface defects based on particle swarm optimization and one-class support vector machine[J]. Advances in Mechanical Engineering，2016，8（11）：168781401667766.

[8]    LI W B，LU C H，ZHANG J C. A local annular contrast based real-time inspection algorithm for steel bar surface defects[J]. Applied Surface Science，2012，258（16）：6080-6086.

[9]    QIAN X L，ZHANG H Q，YANG C X，et al. Micro-cracks detection of multicrystalline solar cell surface based on self-learning features and low-rank matrix recovery[J]. Sensor Review，2018，38（3）：360-368.

[10]  GAO G S，ZHANG D，LI C L，et al. A novel patterned fabric defect detection algorithm based on GHOG and low-rank recovery[C]//2016 IEEE 13th International Conference on Signal Processing. Chengdu：IEEE，2016：1118-1123.

[11]  CEN Y G，ZHAO R Z，CEN L H，et al. Defect inspection for TFT-LCD images based on the low-rank matrix reconstruction[J]. Neurocomputing，2015，149：1206-1215.

[12]  王忠美，楊晓梅，顾行发. 基于鲁棒主成分分析的红外图像小目标检测[J]. 兵工学报，2016，37（9）：1753-1760.

[13]  杜海顺，张旭东，金勇，等. 基于Gabor低秩恢复稀疏表示分类的人脸图像识别方法[J]. 电子学报，2014，42（12）：2386-2393.

[14]  姚明海，李洁，王宪保. 基于RPCA的太阳能电池片表面缺陷检测[J]. 计算机学报，2013，36（9）：1943-1952.

[15]  徐黎明，吕继东. 基于同态滤波和K均值聚类算法的杨梅图像分割[J]. 农业工程学报，2015，31（14）：202-208.

[16]  史加荣，郑秀云，魏宗田，等. 低秩矩阵恢复算法综述[J]. 计算机应用研究，2013，30（6）：1601-1605.

[17]  WRIGHT J，GANESH A，RAO S，et al. Robust principal component analysis：exact recovery of corrupted low-rank matrices [J]. Neural Computation，2009，20（2）：566-567.

[18]  杨剑哲，孙巧榆，王君，等. 基于改进增广拉格朗日乘子法的鲁棒性主成分分析[J]. 哈尔滨工业大学学报，2015，47（11）：27-33.