基于SEM的高校计算机教育评估模型研究

张勇，鲁小兰

［摘 要］ 计算思维反映的是利用计算机技术解决实际问题的思维方法，计算思维能力和意识的培养是当前大学计算机教育教学改革的重点方向。从计算思维意识视域出发，采用结构方程模型（SEM）对计算机课程兴趣、教学满意度、教学投入和计算机思维意识进行了检验。结果表明：基于计算机课程兴趣、教学满意度、教学投入和计算机思维意识的结构方程模型有效，但学生对计算机课的兴趣不会直接影响他们的计算机思维意识，只有当学生对教学感到满意并因对计算机课的兴趣而投入“计算机”课程中时，这种兴趣才会对学生培养和提高计算机思维意识产生影响。

［关键词］ 计算机课程兴趣；教学满意度；课程投入；计算机思维意识

［基金项目］ 2020年度湖北省教育科学规划重点课题“管办评分离视角下湖北省高等教育第三方评估体系建设研究”（2020GA057）；2022年度湖北文理学院“课程思政”教学研究项目“Python编程实践课程的思政设计与探索”（SZ2022010）

［作者简介］ 张 勇（1980—），男，湖北潜江人，博士，湖北文理学院计算机工程学院讲师，主要从事智能计算研究；鲁小兰（1979—），女，湖北潜江人，博士，湖北文理学院经济管理学院副教授，主要从事公司治理研究。

［中图分类号］ G642.0［文献标识码］ A［文章编号］ 1674-9324（2023）11-0021-04［收稿日期］ 2022-05-27

引言

计算思维是周以真教授于2006年首次提出并系统定义的一种基于计算机思想的有效的问题解决方法。2010年教育部高等学校计算机科学与技术教学指导委员会明确将计算思维列入计算机专业人才的四大专业能力之一。2013年，陈国良院士提出计算思维教育的目的是培养一种思维意识习惯［1］，并于2020年提出计算机思维2.0。通过培养计算思维意识，学生可以学习掌握如何分析新信息和处理新问题，解决问题的能力会得到提升。因此，在当代大学计算机教学中，教学的主要目的不仅是要培养学生的计算机技能，还要培养学生运用计算思维正确解决实际问题的能力，以及培养学生观察理解抽象语言的计算机思维意识［2］。近几年来，我国计算机课程教学发生了许多变化，取得了一定的进展，教学内容从简单的计算机理论知识到培训应用技能和思维能力不断变化与丰富，教学难度也在不断增加。这些变化的目的就是要将计算思维能力和意识的培养作为大学计算机课程教育的基本要求和具体目标［3］。基于此，本文结合大学计算机教育实际情况，从计算思维意识视域出发，选取结构方程模型（SEM），探究计算机课程学习兴趣、课程投入、教学满意度等影响因素对计算机思维意识的影响程度，以期为大学计算机教育评估提供科学和个性化的参考建议。

一、研究对象与方法

（一）研究对象

采用分层整群抽样的方法，对湖北省高校学生群体进行了问卷调查，覆盖范围主要为所有工科学院的在读本科生。共发放问卷1 400份，回收1 324份，回收率为94.6%。在获得问卷数据后对回收的所有问卷进行筛选，筛出不合格的错误问卷，以保证研究数据的准确，共回收正确问卷1 314份，其中有效问卷1 257份，有效回收率为95.7%。

（二）问卷设计

问卷主体由计算机课学习兴趣、课程投入、教学满意度、计算机思维意识4个量表组成。其中，计算机课兴趣量表包括11个问题，涵盖三个维度；课程投入量表包括18个问题，涵盖四个维度；教学满意度量表包括12个问题，涵盖三个维度；计算机思维意识量表包括2个问题，涵盖两个维度。采用李克特5级量表设置问卷问题（即5非常符合、4符合、3一般符合、2不符合、1非常不符合）。

（三）数据的信度和效度检验

问卷数据回收后，首先利用SPSS 22.0对问卷有关数据分别进行描述性统计分析及信度、效度的检验。经分析，“计算机”课程兴趣KMO=0.887，课程投入KMO=0.912，教学满意度KMO=0.895，计算机思维意识KMO=0.952，表明数据有较好的效度。信息分析采用Cronbachs Alpha系数，量表的总体Alpha系数在0.788～0.921之间，表明数据有较好的信度。

（四）SEM构建

结构方程模型（SEM）是一种分析复杂的协方差结构，对多元数据进行统计分析，发掘潜在的、互依的或相互影响的因果变量的方法［4］。本文根据结构方程模型理论，运用AMOS 24.0软件对影响学生计算思维意识的因素进行结构方程拟合与路径分析，解释各个因素与计算思维意识的关系及其作用效果。

二、结果与分析

（一）模型拟合度的评价

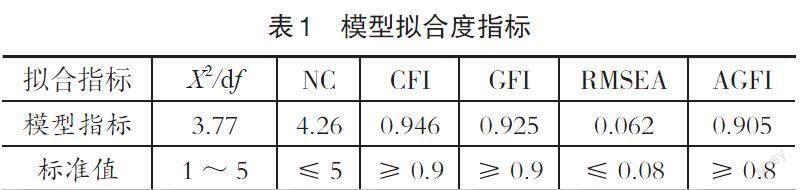
拟合度指标是指理论模型与实际数据的一致性程度，良好的模型拟合度保证了模型的有效性和可信度［5］。采用AMOS 24.0中的最大似然法进行参数估计，对所提出的理论模型进行了假设检验，最终得出的模型拟合指数如表1所示。理论模型的各项拟合指标实际值与标准值相比较，均达到合理的范围，可知各项指标拟合度均较好，说明所构建的假设模型是可以接受的。

（二）假设检验结果分析

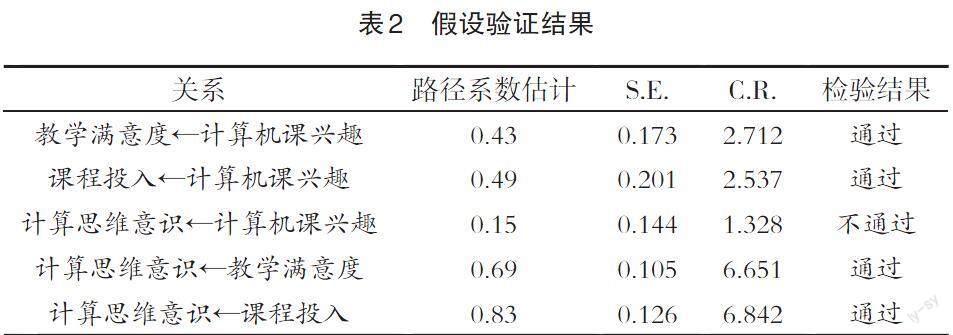
对于初步构建的理论模型，采用最大似然估计法，对路径系数进行参数估计，各潜变量间的结构关系及其标准化后的路径系数、标准差等假设检验结果如表2所示。其中S.E.和C.R.是一个统计量，S.E.是参数标准差，C.R.是参数估计值和标准差之比。可以发现，除了计算机课程兴趣与计算思维意识之间的作用关系假设没有通过检验，其他的研究假设均通过了检验。

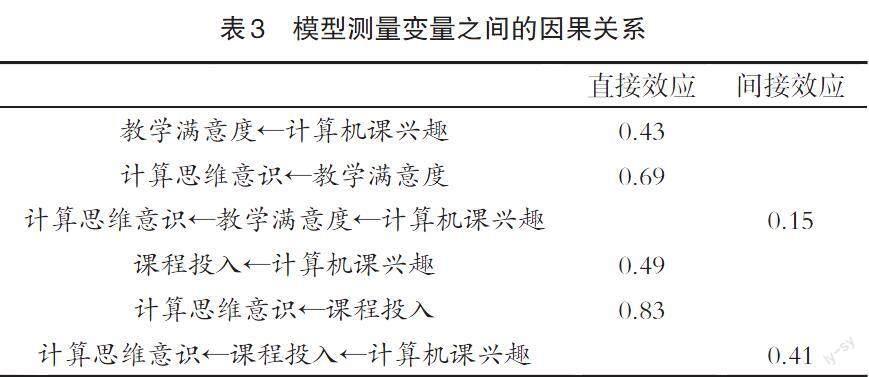
表3给出了研究模型的测量变量之间的因果关系。直接效应是由原因变量对结果变量的直接影响，效应量大小为两个变量间的路径系數；间接效应则是原因变量通过影响中介变量，从而对结果变量产生的间接影响，当只有一个中介变量时，效应量大小为两个路径系数的乘积。

根據表3的验证结果，“计算机课兴趣”对教学满意度的直接效应量为0.43。说明学生对计算机课的社会就业、成就感、专业技能等兴趣越高，学生对课程管理、教学指导、教学环境的满意度越高。

“计算机课兴趣”对“课程投入”的直接效应量为0.49。说明学生对计算机课的社会就业、成就感和专业技能等兴趣越高，学生对计算机课的目的性、内容性、挑战性、综合性等方面的课程投入就越高。

“计算机课兴趣”对“计算思维意识”直接效应量为0.15，可以认为“计算机课兴趣”对“计算思维意识”没有直接影响，但“计算机课兴趣”通过影响“教学满意度”可以对“计算思维意识”产生间接影响，间接效应量为0.43×0.36≈0.15；同理，“计算机课兴趣”通过影响“课程投入”可以对“计算思维意识”产生间接影响，间接效应量为0.49×0.83≈0.41。

“教学满意度”对“计算思维意识”的直接效应量为0.69。这说明课程管理、教学指导、教学环境等满意度因素越高，培养和产生计算思维意识的可能性就越高。

“课程投入”对“计算思维意识”的直接效应量为0.83。这说明学生的目的性、内容投入性、挑战性、整合性等课程投入因素越高，培养和产生计算思维意识的可能性就越高，并且“课程投入”对“计算思维意识”的直接影响要比“教学满意度”对“计算思维意识”的直接影响更加显著。

三、结论与建议

（一）结论

本次研究应用结构方程模型验证了各个变量之间的相关性。首先，明确了计算机课程兴趣对教师教学满意度和学生课程投入均有正向影响，但影响程度较小，并且计算机课程兴趣对计算思维意识基本没有影响；其次，教师教学满意度及学生的课程投入均对计算思维意识产生正向影响，并且影响程度较大；最后，计算机课兴趣通过影响教师教学满意度和学生课程投入对学生计算思维意识有较小的间接影响。因此，基于计算机课程兴趣、教学满意度、课程投入和计算思维意识的计算机教学评价模型是有效的。

（二）建议

为了更好地适应信息化和人工智能时代背景，培养学生运用计算思维能力去解决专业领域中具体问题的意识和能力，高校计算机的课程要在教学过程中强化学生兴趣因素，让学生更积极地投入和参与到计算机课的教学中，并通过加强课程管理、教学指导、教学环境等途径提高学生对教学结果的满意度。具体提出了以下几点建议。

第一，树立科学明确的教学目标。计算机技术日新月异，对于传统的教学模式来讲，学生对计算机课程的兴趣并不高。教师必须积极转变教学理念，与时俱进，以适应现代信息技术发展的要求。教学要从培养学生解决问题能力和计算思维能力两方面入手，以知识和技能掌握为基础，然后向计算思维能力培养进行递进，逐步提高学生的计算思维和创新能力。

第二，设计科学的计算机课程体系。为了满足教学实际需要和学生对计算机教学的需求，首先，教师应在传统原有教学内容的基础上进行创新和完善，合理、科学地构建计算机课程体系。在学生充分掌握了相关的计算机理论知识的基础上，增加一些实践案例和课题设计，培养学生运用理论知识的实践能力和创新思维。其次，教师应积极学习先进技术，及时向学生介绍当前科学前沿的新技术，激发学生的学习兴趣，让学生充分领略计算机科学的魅力。

第三，积极创新计算机教学方法。在教学过程中如果是理论教授和实验操作的简单重复，会让计算机课程变得枯燥和乏味。大学计算机教师应创新教学方法，营造轻松愉快的学习环境和氛围，充分调动学生的积极性，鼓励学生根据教学内容提出有挑战性的教学问题，有效地引导学生探索问题并找出问题的核心，培养学生的探索性思维和发散性思维，让学生获得成就感。同时，采用案例教学法，通过师生之间讨论问题，引导学生思考、归纳和总结，并且对学生计算思维能力进行专项训练，加强学生对计算思维的理解。

参考文献

［1］陈国良，董荣胜.计算思维的表述体系［J］.中国大学教学，2013（12）：22-26.

［2］薛佳楣，苏晓光，刘越，等.基于计算思维能力培养的大学计算机基础教学策略［J］.电脑知识与技术，2021，17（1）：197-198.

［3］谢景伟.计算机思维与大学计算机课程改革的基本思路［J］.中国多媒体与网络教学学报（中旬刊），2018（7）：37-38.

［4］荣泰生.Amos与研究方法［M］.重庆：重庆大学出版社，2019：7.

［5］李硕豪，杨海燕.基于结构方程模型的高校理科教学学生满意度研究：以东中西部9所高校为例［J］.现代大学教育，2015（4）：80-92.

Research on SEM Evaluation Model of Computer Education in Universities

ZHANG Yonga， LU Xiao-lanb

（a. Computer School， b. College of Economics & Management， Hubei University of Arts and Science， Xiangyang， Hubei 441053， China）

Abstract： Computational thinking reflects the thinking method of using computer technology to solve practical problems. The cultivation of computational thinking ability and consciousness is the key direction of the current university computer education and teaching reform. Starting from the perspective of computational thinking consciousness， this paper uses structural equation model（SEM） to test the computer course interest， teaching satisfaction， teaching input and computer thinking consciousness. The results show that the structural equation model based on the course interest， teaching satisfaction， teaching input and computational thinking consciousness is effective， but the students interest in the computer courses will not directly lead to their computer thinking consciousness. Only when students are satisfied with the teaching and only when they are really interested in the computational courses， this interest will have an impact on students cultivation and the improvement of computer thinking consciousness.

Key words： interest in computer courses; teaching satisfaction; course input; computer thinking consciousness