基于虚拟同步机的参数自适应频率控制策略
2023-05-30杨智伟孙俏王凡郭通
杨智伟 孙俏 王凡 郭通
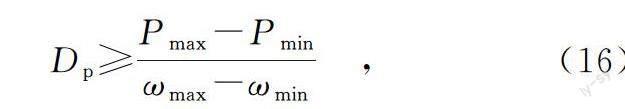
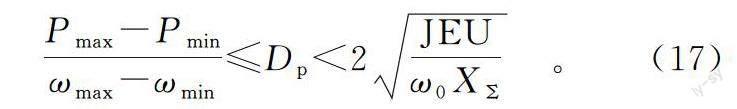
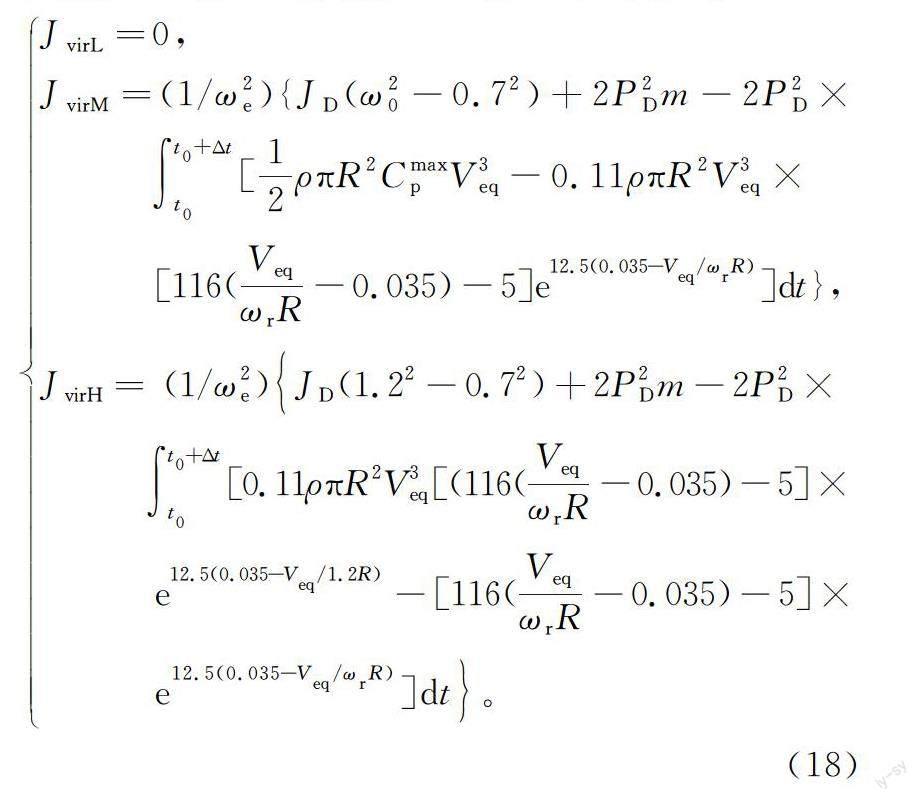
摘 要:為了解决传统虚拟同步机无法根据风机运行状态自适应调整控制参数这一问题,
提出了一种基于虚拟同步机的参数自适应频率控制策略。首先,建立虚拟同步机控制方式下的双馈风机模型,并利用根轨迹法分析虚拟惯量和阻尼系数对系统稳定性的影响。在此基础上,提出自适应虚拟同步机控制策略与参数整定方法,建立虚拟惯量和阻尼系数与系统频率的函数关系,并根据风机运行状态确定参数初始值,实现虚拟同步机控制参数随频率变化的动态调整。最后,在Matlab/Simulink中进行仿真。结果表明,所提频率控制策略实现了虚拟惯量和阻尼系数的自适应调节,能够充分利用风机旋转动能,有效抑制频率跌落并提升频率恢复速度,提高系统频率稳定性,有助于将新能源有效融入电网,规避电网安全问题,并为新型电力系统建设提供有效参考。
关键词:电力系统及其自动化;双馈风机;虚拟同步机;虚拟惯量;阻尼系数
中图分类号:TM727
文献标识码:A
DOI: 10.7535/hbgykj.2023yx02003
Parameter adaptive frequency control strategy based on virtual synchronous generator
YANG Zhiwei1, SUN Qiao2, WANG Fan3, GUO Tong4
(1.Big Data Center, State Grid Company Limited, Beijing 100053,China; 2.Management Training Center, State Grid Jibei Electric Power Company Limited, Beijing 102401,China; 3.Skills Training Center, State Grid Jibei Electric Power Company Limited, Baoding, Hebei 071051,China;4.Xiong′an New Area Power Supply Company, State Grid Hebei Electric Power Company Limited, Xiong′an New Area, Hebei 071700,China)
Abstract:In order to solve the problem that the traditional virtual synchronous machine cannot adjust the control parameters adaptively according to the running state of the fan, a parameter adaptive frequency control strategy based on virtual synchronous machine was proposed. Firstly, a double-fed wind turbine model under virtual synchronous machine control mode was established, and the influence of virtual inertia and damping coefficients on system stability was analyzed by using root locus method. Based on this, an adaptive virtual synchronous machine control strategy and parameter tuning method were proposed. This method established a functional relationship between the virtual inertia and damping coefficients and the system frequency, and determined the initial parameter values based on wind turbine operating conditions, achieving dynamic adjustment of virtual synchronous machine control parameters with frequency changes. Finally, simulation was carried out in Matlab/Simulink. The results show that the proposed frequency control strategy achieves adaptive adjustment of virtual inertia and damping coefficient, fully utilizes the rotational kinetic energy of the wind turbine, effectively suppresses frequency drops and improves frequency recovery speed, and enhances system frequency stability. The proposed method can fully utilize the rotational kinetic energy of the wind turbine, effectively suppress the frequency drop, improve the frequency recovery speed, and enhance the system frequency stability.
The proposed strategy is helpful to integrate new energy into the power grid effectively, avoid the problem of power grid security, and provide an effective reference for the construction of new power system.
Keywords:electric power system and its automation; doubly-fed induction generator; virtual synchronous generator; virtual inertia; damping coefficient
在“碳中和、碳达峰”的愿景下,高比例新能源发电正逐步取代传统化石能源,在能源结构中占据主导地位[1-2]。2022年,中国新增风电与光伏装机容量有望达到120 GW,同比增长20%。但高比例新能源的接入与高比例电力电子设备的应用也给电力系统的频率安全带来了两大挑战[3]:一方面,新能源机组大多通过电力电子设备并网,其有功功率和系统频率解耦,通常无法在扰动后响应系统频率变化[4];另一方面,随着新能源大量取代传统同步机组,以传统同步机组为主的调频资源已无法满足系统调频需求。除此之外,交直流互联电网的形成也使系统发生大功率扰动及频率扰动的风险增加。例如,2015年发生的锦苏直流双极闭锁故障,直流功率损失达到了4 902 MW,直接导致江苏电网频率跌落了0.413 Hz。事故分析报告指出,新能源大量接入造成系统惯量响应和一次调频能力不足是造成此事件的根本原因。
随着高比例新能源系统频率问题逐渐凸显,中国在《电力系统安全稳定导则》中对新能源机组的惯量支撑能力提出了明确要求[5];在《风力发电机组电网适应性测试规程》中进一步明确了当风电机组的有功出力大于20%的额定功率时,其应具备响应系统频率变化率的能力。世界范围内各国均规定新能源机组在承担正常发电任务的同时,也要具备一定的调频能力,例如对风电机组的电力电子设备进行附加控制,使其参与调频[6]。因此,有学者提出了虚拟同步机(virtual synchronous generator,VSG)的概念,通过附加控制使风电机组具有和同步机组相似的频率响应能力[7]。
国内外研究表明同步机组的调控技术和保护方式在VSG中仍可适用[8-9]。当电网发生扰动时,风电机组可通过VSG控制有效提高系统惯量,从而提升频率稳定性[10]。然而传统的VSG控制采用恒定参数,无法发挥逆变器灵活可控的优点,导致调频效果不佳[11]。因此,参数自适应的改进VSG控制策略应运而生。例如,文献[12]构造频率变化率与虚拟惯量的关系,实现了虚拟惯量的自适应调整,提高了微电网的频率稳定性。文献[13]建立频率偏差与虚拟惯量的关系,实现了虚拟惯量自适应调节,提升了频率暂态响应速度。文献[14]建立了虚拟惯量与系统频率偏差及其变化率的函数,实现了虚拟惯量的自适应调节。然而,上述文献未考虑阻尼系数对系统频率的影响,导致频率超调的改善效果不够明显。在此基础上,文献[15]提出一种基于稳态频率偏差的阻尼系数自适应控制策略,同时设置稳态时的阻尼系数为零,有效抑制系统振荡。文献[16]提出了虚拟惯量和阻尼协同自适应调整策略,有效提升了扰动后系统的频率响应能力。然而大部分方法仅考虑了单一参数对频率稳定性的影响,对虚拟惯量和阻尼系数协同优化控制的研究较少。
为充分发挥VSG的优势,本文提出虚拟转动和阻尼系数自适应的频率控制方法。首先,建立虚拟同步机小信号模型,提出基于广义根轨迹的频率控制参数分析方法;然后,分析虚拟惯量和阻尼系数对系统稳定性的影响,提出一种基于虚拟同步机的参数自适应频率控制策略及其参数整定方法,实现虚拟惯量和阻尼与频率的函数关系构建;最后,通过仿真实验验证所提方法能否有效抑制频率跌落并提升频率恢复速度。
1 虚拟同步机控制原理
VSG控制是在双馈风机(double-fed induction generator,DFIG)的逆变器控制中引入同步机组的转子运动方程和电磁方程,使其在并网时具有和同步机组相似的惯量响应特性[17]。VSG控制拓扑如图1所示。图中双馈风机等效为原动机,施加控制的变流器等效为同步发电机[18]。其中,有功-頻率控制环节能够模拟同步机组的调频功能;无功-电压控制环节能够模拟同步机组的励磁调节功能;电压-电流双环控制能够计算电流的参考值对其进行跟踪,同时能够输出调制电压。
VSG有功-频率控制的数学模型如式(1)所示。
式中:J为虚拟惯量系数;Dp为阻尼系数;θ为虚拟功角;Pe为VSG的电磁功率;Pm为VSG机械功率;ω为VSG的角速度;ω0为额定角速度;Pref为双馈风机最大功率跟踪控制的功率参考值;k为VSG一次调频系数。ω一般在额定角速度ω0附近变化,因此在计算转矩差Tm-Te时可以认为ω≈ω0。
由式(1)可知,VSG控制使双馈风机具有与同步机组相似的惯量和一次调频特性,虚拟惯量J和阻尼系数Dp是影响VSG运行稳定的主要参数,同时直接影响其调频能力。基于上述模型,建立了VSG内电势与DFIG功率的数学联系[19]。
另外,双馈风机的功率变化与运行状态密切相关,其机械功率Pmw的表达式见式(2):
式中:ρ为空气密度;λ为叶尖速比;β为桨距角;R为桨叶半径;v为风速;Cp为风能利用系数;ω为双馈风机转子转速。
因此,本文在分析虚拟惯量J和阻尼系数Dp对系统稳定性影响的基础上,考虑风电机组运行特性,提出参数自适应的VSG频率控制策略,以保证最优的调频效果。
2 虚拟惯量和阻尼系数对系统频率特性的影响
本节主要研究虚拟惯量和阻尼系数的影响,因此不考虑虚拟同步机的一次调频,即式(1)所示机械功率Pm=Pref。
如图1所示,设DFIG输出电压为E∠θ,电网电压为U∠θ,DFIG输出阻抗Zs=Rs+jXs,电网线路阻抗Zg=Rg+jXg。定义等效阻抗ZΣ=Zs+Zg=RΣ+jXΣ。
由于DFIG输出电压和电网电压之间的阻抗一般呈阻感性,可等效为一个与Xg串联的电感,从而XΣ>>RΣ。
考虑到VSG稳态运行时,其输出电压与电网电压之间的相位差很小,存在sin θ≈θ。因此,DFIG馈入电网的有功功率
可表示为式(3):
令式(1)和式(3)中状态变量等于稳态量和小扰动量之和,如式(4)所示。
式中:ωs,θs,Pes,Prefs分别为VSG输出电压的角频率、功角、有功功率和有功功率参考值的稳态值;
Δω,Δθ,ΔPe,ΔPref分别对应上述参数在稳态工作点附近的小扰动量。
基于上述内容,推导VSG有功-频率控制环节的小信号模型。将式(4)代入式(1)、式(3),可得式(5):
式(5)中等式两边同时消去直流量,可得式(6):
由式(6)可得VSG有功-频率控制在s域内的小信号模型如图2所示。
图2所示系统的开环传递函数为式(7):
闭环传递函数为式(8):
系统的闭环特征方程为式(9):
图2所示系统的固有震荡频率ωn和阻尼系数ζ如式(10)所示:
由式(9)和式(10)可知,系统的等效开环传递函数如式(11)计算:
式中K=Dp/J。
VSG参数如表1所示。根据式(11)绘制参数K的广义根轨迹,如图3所示。
由图3可以看出,闭环极点均在s域的左半平面,因此系统能够保持稳定。当J恒定时,随着Dp增大,系统阻尼增大,此时系统的超调量减小,调整时间变长。这表明随着Dp的增大,扰动后系统频率的暂态波动趋于平稳,但频率恢复所需的时间有所增加。当Dp恒定时,随着J增大,闭环极点逐渐越靠近原点,此时系统的响应速度减慢,同时特征根的虚部减小,因此系统頻率变化过程更加平稳,但当J持续增加时,极点离原点过近,会导致VSG并网稳定性变差。
3 基于改进遗传算法的自适应虚拟惯量控制策略
3.1 自适应虚拟惯量原理
假设系统在t0时刻发生扰动,虚拟同步机的角速度偏差及其变化率曲线如图4所示。
1)在t0~t1内,dΔω/dt>0,Δω>0。dΔω/dt在t0时刻突增后迅速跌落,t1时刻减小至0;Δω从t0时刻开始增大,t1时刻到达峰值。因此在t0~t1内,需要抑制角速度的快速变化,应选择较大的虚拟惯量J。但随着J的增加,系统响应速度减慢,此时减小阻尼系数Dp虽能提升响应速度,但导致系统超调量增大,即频率最低点增大。另外,增大阻尼系数Dp能减小本时段的角速度偏差,但会使调整时间进一步增加,因此在此阶段可保持Dp不变。
2)在t1~t2内,dΔω/dt<0,Δω>0。dΔω/dt在此区间内从0开始先减小后增大,Δω从峰值减小至0。因此在t1~t2内,需要加快角速度偏差的变化,使其尽快恢复,应选择较小的虚拟惯量J,同时采用较大的阻尼系数Dp进一步抑制超调量,减小角速度偏差,有利于频率尽快稳定。
3)在t2~t3内,dΔω/dt<0,Δω<0。dΔω/dt在此区间为负值,其绝对值逐渐减小至0;Δω从0减小至最小值。因此在t2~t3内应选择较大的虚拟惯量J,抑制角速度偏差的变化。本时段内,角速度及其变化率情况与t0~t1时段相似,因此在此阶段仍需保持Dp不变。
4)在t3~t4内,dΔω/dt>0,Δω<0。dΔω/dt在此区间为正值,变化较为缓慢,Δω从最小值增加至0。因此在t3~t4内应选择较小的虚拟惯量J,加快角速度的恢复,同时适当增大阻尼系数Dp,减小角速度偏差。
综上所述,为提高系统频率稳定性,在dΔω/dt与Δω同号区间内,应选取较大的虚拟惯量J和恒定的阻尼系数Dp,在二者异号的区间内,应选取较小的虚拟惯量J和较大的阻尼系数Dp。J和Dp的调整规律如表2所示。
由表2可得参数自适应频率控制策略,如式(12)和式(13)所示:
式中:K1和K2分别为虚拟惯量和阻尼系数的自适应系数;N1和N2分别为J和Dp的自适应控制死区,可避免参数因微小波动而进行频繁调整,以增加系统稳定性。
3.2 自适应虚拟惯量参数整定
双馈风机的调频能力与其运行状态密切相关,因此根据风电机组的运行状态合理整定自适应控制策略的初始参数J0,Dp0,K1,K2,才能充分利用风机转子动能。
电力系统频率稳定性指标主要包括:频率变化率(dΔf/dt)、最大频率偏差(Δfmax)和稳态频率偏差(Δfn)。式(14)为本文定义频率稳定评估指标P:
式中:a,b,c为权重系数,可以采用层次分析法确定其数值。
为抑制暂态频率波动,保证系统稳定运行,需要满足的条件如式(15)所示:
同时,VSG角速度应在允许范围内,因此阻尼系数Dp需满足的条件如式(16)所示:
式中:ωmax和ωmin分别为VSG角速度的上下限,Pmax和Pmin分别为风电机组允许输出有功的上下限。
结合式(15)和式(16)可知,阻尼系数Dp的取值范围如式(17)所示:
风机可提供的转动惯量与其运行状态密切相关,因此需要根据式(18)获得不同运行状态下的惯量约束,具体推导过程及式中各个变量含义见文献[20]。
式中:JvirL,JvirM,JvirH分别代表风电机组低、中、高3种风速下可提供的最大虚拟惯量。
在传统遗传算法的基础上引入移民算子,利用改进遗传算法获取自适应控制策略初始参数J0,Dp0,K1,K2的最优组合。通过移民算子实现多个种群之间的并行、协同进化,并将最优个体保存至人工选择算子,同时形成精华种群,用于作为收敛性判断的依据,解决传统遗传算法早熟收敛的缺点,更加适合优化较为复杂的问题[21-22]。目标函数与约束条件如式(19)所示:
式中:Jviri(i表示低、中、高3种风速)为当前风速下最大虚拟惯量;ωr为风电机组的转子转速。
3.3 参数自适应控制算法流程
本文所提参数自适应频率控制策略流程如图5所示。
首先根据式(17)、式(18)计算虚拟惯量和阻尼系数的允许变化范围。其次利用改进遗传算法,根据式(19)所示的目标函数和约束条件,获取自适应控制策略的初始参数J0,Dp0,K1,K2。最后采集电网参数dΔω/dt与Δω,并根据式(12)、式(13)计算对应的虚拟惯量J和阻尼系数Dp,实现调频控制参数优化。
4 算例分析
为验证本文所提自适应频率控制策略的有效性,在Matlab/Simulink中搭建双馈风机的并网仿真模型,2台DFIG并联,均采用VSG控制,系统的拓扑结构如图6所示。其中,Z1和Z2为虚拟同步机的滤波阻抗,Zl1,Zl2,Zl3为线路阻抗。电网的电压等级为0.4 kV,选用恒功率负载。
所用模型的各个参数及其数值如表3所示。
4.1 虚拟惯量和阻尼系数对频率的影响
在表3所示系统参数下,采用传统定参数VSG控制,分析虚拟惯量和阻尼系数对频率的影响。设置VSG并网时系统仅接入负荷1,第2 s接入负荷2,仿真时长10 s。图7为不同参数下的频率曲线。
由图7 a)可以看出,虚拟惯量J的增加可提高系统的频率稳定性,减小频率超调量,但导致频率恢复速度降低。由图7 b)可以看出,阻尼系数Dp的增加会导致频率超调量减小,频率恢复速度提升。但随着Dp持续增加,频率恢复速度反而下降。
4.2 自适应频率控制的有效性验证
4.2.1 負荷扰动下的优化效果
VSG并网时系统仍仅接入负荷1。扰动设置为在第2 s接入负荷2,在第4 s负荷1减少40 kW。自适应阈值N1=2,N2=0.1。按照3.2节所述方法确定VSG控制参数,如表4所示。
图8对比了不同控制策略下扰动后电力系统频率的变化情况。控制策略如下:
1)常规恒定参数VSG控制;
2)仅虚拟惯量J自适应控制[13];
3)虚拟惯量J和阻尼系数Dp自适应控制[16];
4)本文所提的自适应VSG控制策略。
由图8可以看出,恒定参数VSG控制不能调节控制参数,无法同时优化超调量和恢复速度。参数自适应控制策略能够在一定程度上提升暂态频率稳定性,但仅虚拟惯量J自适应控制的效果并不理想,虽然能够有效抑制暂态频率变化,但是频率恢复速度有所下降。与常规自适应控制相比,在本文所提虚拟惯量和阻尼自适应控制下,系统超调量更小,频率恢复更快,验证了本文所提方法能够兼顾频率稳定性和恢复速度,提升系统发生负荷扰动后的频率稳定性。
4.2.2 短路故障下的优化效果
为验证所提的参数自适应频率控制策略在短路故障下的优化效果,本节设置在Zl1和Zl2所连线路的中点发生单相短路接地故障,系统参数选择与4.2.1节相同。仿真时长共计4.5 s,第2 s故障发生,0.5 s后故障切除。图9对比了不同控制策略下故障后电力系统频率的变化情况。
由图9可以看出,恒定参数VSG控制无法同时兼顾超调量和恢复速度,恢复速度相对较快,但超调量较大。本文所提方法相较于常规自适应控制,能够有效抑制短路故障后的频率暂态波动,同时具有较快的恢复速度,能够有效提升系统短路故障发生后的频率稳定性。
5 结 语
本文提出了一种基于虚拟同步机的参数自适应频率控制策略,用于自适应地调整虚拟惯量和阻尼系数,充分利用风机旋转动能,提高系统频率稳定性。研究结论如下:
1)建立了VSG小信号模型,提出了基于广义根轨迹的系统稳定性分析方法。分析表明,虚拟同步机的虚拟惯量和阻尼系数过大或过小均不利于系统稳定,需要选择恰当参数才能获得最佳调频效果。
2)基于系统角速度变化曲线,分析了不同时间段内VSG控制参数的选择对频率稳定性的影响,提出了虚拟惯量和阻尼系数自适应的频率控制策略。仿真结果表明,与常规的VSG控制策略相比,所提策略能够有效改善系统频率响应特性。
3)所提出的基于改进遗传算法的参数自适应频率控制策略的参数整定方法,考虑了双馈风机的运行状态,能够提升系统运行的稳定性,兼顾频率稳定性和恢复速度,有效减小最大频率偏差,加快频率恢复。
本文进行了仿真验证但并未进行实验验证,这是本文的不足之处,也是未来研究需要补充之处。与此同时,可结合虚拟同步机的特性,进一步优化自适应控制策略的触发机制,以兼顾系统的动态性能与稳定性。
参考文献/References:
[1] 靳伟,陈岩,王文宾,等.薄弱配电网高比例分布式光伏并网消纳规划研究[J].河北工业科技,2020,37(3):151-158.
JIN Wei,CHEN Yan,WANG Wenbin,et al.Research on grid-connection consumption planning of high proportion distributed photovoltaic in weak distribution network[J].Hebei Journal of Industrial Science and Technology,2020,37(3):151-158.
[2] 王博,杨德友,蔡国伟.高比例新能源接入下电力系统惯量相关问题研究综述[J].电网技术,2020,44(8):2998-3006.
WANG Bo,YANG Deyou,CAI Guowei.Review of research on power system inertia related issues in the context of high penetration of renewable power generation[J].Power System Technology,2020,44(8):2998-3006.
[3] 康重庆,姚良忠.高比例可再生能源电力系统的关键科学问题与理论研究框架[J].电力系统自动化,2017,41(9):2-11.
KANG Chongqing,YAO Liangzhong.Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J].Automation of Electric Power Systems,2017,41(9):2-11.
[4] 庹瑾,罗冰冰,刘岑岑,等.非理想电网下直驱风力发电功率和电流平衡控制[J].河北工业科技,2020,37(5):343-351.
TUO Jin,LUO Bingbing,LIU Cencen,et al.Power and current balance control of direct-driven wind power generation under non-ideal grid conditions[J].Hebei Journal of Industrial Science and Technology,2020,37(5):343-351.
[5] BEVRANI H,GHOSH A,LEDWICH G.Renewable energy sources and frequency regulation:Survey and new perspectives[J].IET Renewable Power Generation,2010,5(4):438-457.
[6] GB 38755—2019,电力系统安全稳定导则[S].
[7] DRIESEN J,VISSCHER K.Virtual synchronous generators[C]//2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century.Pittsburgh:IEEE,2008:1-3.
[8] LI Dongdong,ZHU Qianwei,LIN Shunfu,et al.A self-adaptive inertia and damping combination control of VSG to support frequency stability[J].IEEE Transactions on Energy Conversion,2017,32(1):397-398.
[9] 國家能源局.具备虚拟同步机功能的新能源电站在河北建成投运[EB/OL].(2017-12-29)[2022-08-23].http://www.nea.gov.cn/2017-12/29/c_136859301.htm.
[10]章艳,高晗,张萌.不同虚拟同步机控制下双馈风机系统频率响应差异研究[J].电工技术学报,2020,35(13):2889-2900.
ZHANG Yan,GAO Han,ZHANG Meng.Research on frequency response difference of doubly-fed induction generator system controlled by different virtual synchronous generator controls[J].Transactions of China Electrotechnical Society,2020,35(13):2889-2900.
[11]FRACK P F,MERCADO P E,MOLINA M G,et al.Control strategy for frequency control in autonomous microgrids[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2015,3(4):1046-1055.
[12]程冲,杨欢,曾正,等.虚拟同步发电机的转子惯量自适应控制方法[J].电力系统自动化,2015,39(19):82-89.
CHENG Chong,YANG Huan,ZENG Zheng,et al.Rotor inertia adaptive control method of VSG[J].Automation of Electric Power Systems,2015,39(19):82-89.
[13]程启明,余德清,程尹曼,等.基于自适应旋转惯量的虚拟同步发电机控制策略[J].电力自动化设备,2018,38(12):79-85.
CHENG Qiming,YU Deqing,CHENG Yinman,et al.Control strategy of virtual synchronous generator based on adaptive rotational inertia[J].Electric Power Automation Equipment,2018,38(12):79-85.
[14]章伟明,赵巧娥,刘毓梅,等.孤岛模式自适应转动惯量VSG逆变电源控制策略[J].电力系统及其自动化学报,2019,31(2):95-100.
ZHANG Weiming,ZHAO Qiaoe,LIU Yumei,et al.VSG inverter power source control strategy with adaptive rotary inertia in island mode[J].Proceedings of the CSU-EPSA,2019,31(2):95-100.
[15]许崇福,李菀茹,徐宁一,等.应用于储能变流器的虚拟同步发电机阻尼特性分析与改进[J].电网技术,2020,44(5):1656-1663.
XU Chongfu,LI Wanru,XU Ningyi,et al.Analysis and improvement of damping characteristics of virtual synchronous generator control applied to energy storage converter[J].Power System Technology,2020,44(5):1656-1663.
[16]杨赟,梅飞,张宸宇,等.虚拟同步发电机转动惯量和阻尼系数协同自适应控制策略[J].电力自动化设备,2019,39(3):125-131.
YANG Yun,MEI Fei,ZHANG Chenyu,et al.Coordinated adaptive control strategy of rotational inertia and damping coefficient for virtual synchronous generator[J].Electric Power Automation Equipment,2019,39(3):125-131.
[17]吕志鹏,盛万兴,刘海涛,等.虚拟同步机技术在电力系统中的应用与挑战[J].中国电机工程学报,2017,37(2):349-360.
LYU Zhipeng,SHENG Wanxing,LIU Haitao,et al.Application and challenge of virtual synchronous machine technology in power system[J].Proceedings of the CSEE,2017,37(2):349-360.
[18]王淋,巨云涛,吴文传,等.面向频率稳定提升的虚拟同步化微电网惯量阻尼参数优化设计[J].中国电机工程学报,2021,41(13):4479-4489.
WANG Lin,JU Yuntao,WU Wenchuan,et al.Optimal design of inertia and damping parameters of virtual synchronous microgrid for improving frequency stability[J].Proceedings of the CSEE,2021,41(13):4479-4489.
[19]POOLLA B K,BOLOGNANI S,LI Na,et al.A market mechanism for virtual inertia[J].IEEE Transactions on Smart Grid,2020,11(4):3570-3579.
[20]高澈,田新首,李琰,等.基于運行状态评估的双馈风机自适应虚拟同步发电机控制[J].电网技术,2018,42(2):517-523.
GAO Che,TIAN Xinshou,LI Yan,et al.Adaptive virtual synchronous generator control of DFIG based on operation state evaluation[J].Power System Technology,2018,42(2):517-523.
[21]黎玺克.遗传算法优化BP神经网络的岩质边坡稳定性预测[J].河北工业科技,2020,37(3):164-169.
LI Xike.Prediction of rock slope stability based on BP neural network optimized by genetic algorithm[J].Hebei Journal of Industrial Science and Technology,2020,37(3):164-169.
[22]POTTS J C,GIDDENS T D,YADAV S B.The development and evaluation of an improved genetic algorithm based on migration and artificial selection[J].IEEE Transactions on Systems,Man,and Cybernetics,1994,24(1):73-86.
