基于决策树模型的地铁线网短时OD客流预测

张恒 秦振华 肖为周 张明娇

摘 要：为了准确获取地铁线网短时OD（起讫点）的客流分布，从而高效协调运输能力和客运需求，结合集成学习思想构建了基于决策树模型的多时间粒度下地铁线网短时OD客流预测模型。首先利用地铁自动售检票数据分析得到线网OD客流出行的时空分布特征，引入多种时空影响因素对全网数据进行训练以及预测，其次分析了地铁线网OD客流量预测精度与时间粒度之间的关系，最后以苏州市地铁为对象进行实例分析。结果表明：相对于其他模型，研究模型不仅可以有效降低预测误差和拟合客流峰值，而且运算时间也节约了数倍，提高了地铁线网短时OD客流预测的准确性和效率。因此，所设计的模型可为地铁运营与控制系统提供重要数据，有助于运营者进行限流措施、行车计划等的制定与调整。

关键词：铁路运输管理；短时OD；客流预测；决策树模型；多时间粒度

中图分类号：U293.13

文献标识码：A

DOI： 10.7535/hbgykj.2023yx02010

Short-time OD passenger flow prediction of subway line network based on decision tree model

ZHANG Heng1，QIN Zhenhua2，XIAO Weizhou1，ZHANG Mingjiao1

（1.School of Rail Transportation， Soochow University， Suzhou， Jiangsu 215000，China; 2.Suzhou Rail Transit Group Company Limited， Suzhou， Jiangsu 215000， China）

Abstract：In order to accurately obtain the short-time OD （origin-destination） passenger flow distribution of the subway line network， so as to efficiently coordinate the transportation capacity and passenger demand， a multi-time granularity short-time OD passenger flow prediction model of subway line network based on the decision tree model was constructed combined with the ensemble learning idea. Firstly， the spatial and temporal distribution characteristics of OD passenger flow on the line network were obtained by using the automatic ticketing data analysis， and various spatial and temporal influencing factors were introduced to train and predict the whole network data. Secondly， the relationship between the prediction accuracy and temporal granularity of OD passenger flow on the metro line network was analyzed. Finally， Suzhou Metro was taken as an example to carry out the case analysis. The results show that， compared with other models， the model can not only effectively reduce the prediction error and fit the peak passenger flow， but also save several times of computing time， which improves the accuracy and efficiency of the short-time OD passenger flow prediction of the subway line network. The designed model can provide important data input for the metro operation and control system， and help operators to formulate traffic restriction measures， travel plans and other strategies.

Keywords：railroad transportation management; short-time OD; passenger flow prediction; decision tree model; multiple time granularity

隨着地铁网络化运营特征的日渐凸显，乘客路径选择的多样化使线网客流分布呈现出随机、复杂等特点，在这样的趋势下预测客流需求愈发困难。短时OD是指在某一较短时间粒度下，所有乘客由起点O到讫点D的出行过程，它反映了线网客流需求的时空分布。OD预测无法像进出站量预测一样直接对客流采用时间序列法预测，因为乘客的出站信息需要经过一段时间才能获取到^［1］，所以OD客流不仅在时间上具有相关性，而且还具有空间相关性^［2］。精准预测地铁线网短时OD客流量可以使运营者提前掌握客流分布动向，并根据短时OD客流预测结果对运营调度进行优化。

目前，短时OD客流预测领域比较成熟的理论主要分为2类。一类是基于统计学理论的方法，如历史平均模型^［3］、时间序列模型^［4］、卡尔曼滤波模型、K近邻算法（K-NN）等。刘洋等^［5］提出了一种基于约束条件的卡尔曼滤波模型对地铁线网OD进行预测，获得了较好的总体估计效果和分时段估计效果。HABTEMICHAEL等^［6］通过K-NN识别客流相似序列，证明了增强型K-NN比卡尔曼滤波模型、普通的K-NN模型预测效果更好。基于统计学理论的方法仅注重客流时间序列的变化，难以考虑除目标变量以外的时空特征，并且在处理具有高维非线性特征的数据时适用性不强。另一类是基于机器学习的方法，如支持向量机模型^［7］、神经网络学习模型、深度学习模型及集成学习模型等。TSAI等^［8］建立了基于时间特征的多时间单位神经网络和并行集成神经网络，实验表明这2种模型的短时客流预测性能优于传统的多层神经网络模型。TIAN等^［9］建立了长短期记忆神经网络（long short-term memory， LSTM）模型对工作日的客流进行短时预测，并与支持向量机单隐藏层前馈神经网络等模型比较，证明所提出的预测模型具有更高的准确率和泛化能力。CHEN等^［10］的研究成果表明，极度梯度提升树（extreme gradient boosting， XGBoost）模型在客流预测性能以及运算效率上都要优于随机森林。上述机器学习模型仅针对单一客流特征进行了建模，而现实中OD客流分布受多种时空特征因素影响。

综上所述，准确预测短时OD客流需求需要在探讨时间维度上OD客流变化规律的同时，挖掘空间维度上与OD客流存在关联性的影响因素。目前既有研究多是选用一种时间粒度进行预测，但单一时间粒度的OD客流变化规律缺乏对比性，不同时间粒度下统计的OD客流的规律性和稳定性存在明显差异^［11］。因此，在总结既有短时OD客流预测方法的基础上，本文利用地铁自动售检票（automatic fare collection， AFC）系統刷卡数据，在多时间粒度场景下，建立基于决策树的LightGBM（light gradient boosting machine）线网短时OD客流预测模型，并考虑OD对类型、天气及空气质量因素、短时进出站客流量因素、工作日与非工作日因素等时空特征对OD客流需求的影响，与多种模型在预测精度、运算效率等方面进行对比，以验证LightGBM模型在线网短时OD客流预测方面的优越性。

1 问题描述

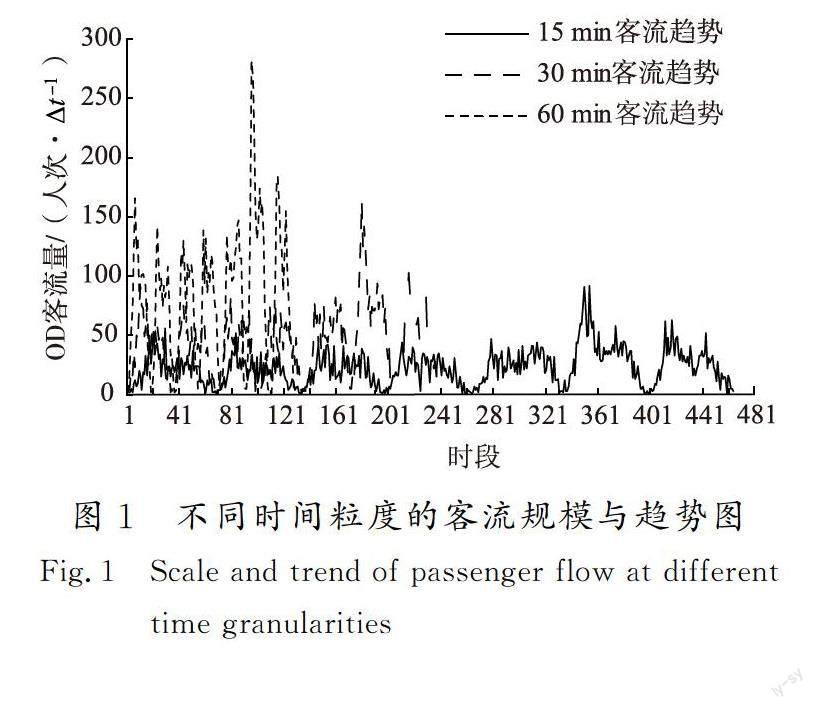
对于客流预测这类回归问题来说，数据和特征决定了预测本身的上限，而模型只是逼近这个上限。先验数据时间粒度的选取决定了短时客流预测的输入^［12］，直接影响到预测结果精度。以线网中任一OD为例，分析其一周内不同时间粒度Δt下的客流趋势，如图1所示，不同时间粒度的OD客流数据规模和趋势存在较大差异，时间粒度越大，一个时段内统计的OD客流量越多，一周内的时段数也越少。

AFC是实现地铁售检票、计费、统计等过程的自动化系统，可详细记录每一乘客的出行信息，但原始数据记录的是每个乘客的进出站时刻，无法直接获取到不同时段内的线网OD信息^［13］。因此将处于5：00～24：00运营时段的1 140 min划分为各时间粒度的时段，将所有乘客的进出站时刻分别与时段匹配并对OD客流进行集计，得到不同时间粒度下的线网OD客流。短时OD预测时间粒度一般不小于15 min且不大于60 min，其中15 min客流和60 min客流通常用于超高峰小时和高峰小时的客流预测与评价，在地铁运营中具有重要实用价值。同时，由图1可知，训练数据规模随时间粒度的成倍扩大而成倍减少，为探究预测精度随时间粒度的变化情况，将30 min时间粒度也纳入后续预测模型之中。综上，本文选取预测的时间粒度Δt为15，30以及60 min，则每天对应的时段个数为76，38，19（1 140/Δt）。定义输入数据的时段总数为T，地铁线网站点个数为N，用yi（t）（i=1，2，…，N2；t=1，2，…，T）表示第t个时段内由车站o前往车站d的OD客流量，N2为线网OD数目，xi（t）=（xi1，xi2，…，xin）表示该时段对应的影响因素特征值，n为影响因素个数，则引入客流影响因素的线网OD客流时间序列可表示为qo，d（t）=［xi（t），yi（t）］。综上，客流预测问题定义为对于线网所有OD，已知前k个时段的OD客流量yi（t）（t=1，2，…，k），结合xi（t）中影响因素的特征值，预测后续l个时段的客流量yi（t）（t=k+1，k+2，…，k+l）。

2 模型构建

对于具有复杂规律的线网OD客流数据，不同OD之间具有的客流趋势往往存在较大差异，训练一个可以从多角度识别客流规律并作出精确预测的单一模型是极为困难的。集成学习是通过构建一系列模型，再使用某种结合策略将各模型的学习结果整合在一起，以获得比单一模型泛化性、准确性更好的模型。它可以有效利用各子模型的预测信息，择优互补，弥补了单一模型在预测时难以学习随机性较强的不均衡数据的弊端，从而提升预测性能。此外，OD客流高峰时段往往比平峰时段高出数倍，因此，需要预测模型具有良好的泛化能力，以避免峰值客流对整体预测结果的拟合造成过大影响。LightGBM是一种基于集成学习的决策树模型，是为了解决梯度提升决策树（gradient boosting decision tree， GBDT）在面对海量数据时耗时过多的问题而提出的。其集成方式旨在降低预测偏差，能够基于泛化性能较弱的学习器构建出很强的集成^［14-15］，因而可以较好地拟合OD峰值客流。相对GBDT需要遍历一层所有叶子节点进行分裂的按层生长（level-wise）策略（如图2所示），LightGBM采用了更为高效的按叶子生长（leaf-wise）策略（如图3所示）。该策略无需考虑同层的其他节点，每次从当前所有叶子中找到分裂增益最大的一个叶子进行分裂，可有效加快训练速度。同时，LightGBM使用单边梯度采样 （gradient-based one-side sampling， GOSS）和互斥特征绑定（exclusive feature bundling，EFB）两大优化方式实现训练过程中对样本数和特征数的减少^［16］，可以快速处理具有多特征的海量地铁线网OD数据。

给定训练数据所有时段的输入qo，d={（x1，y1），（x2，y2），…，（xm，ym）}，其中，m为输入数据集序列长度，xi（i=1，2，…，m）∈xRn，xi为影响因素的特征值，x为输入空间，Rn表示n维向量空间，每个元素为（x1，x2，…，xn）的形式，代表各影响因素的特征值。yi为某时段由车站o前往车站d的OD客流量，yi∈y?R，y为输出空间，R表示实数集，损失函数为L（y，f（x））。综上，LightGBM模型构建流程如下：

1）初始化决策树（弱学习器）f0（x），并使所有训练样本的均值为c。

2）迭代训练s=1，2，…，S个决策树，将影响因素的特征值xi输入决策树中进行训练，计算每个样本i（i=1，2，…，m）的负梯度rs，i，作为下一轮决策树拟合的目标值。

式中：f（x）为上一次迭代生成的决策树；f（xi）为f（x）在样本i的输出值。

3）将（xi，rs，i）作为下一个决策树的训练数据，最小化当前损失函数，求出每个决策树各叶子结点的输出值cs，j。

式中：Rs，j（j=1，2，…，J）表示第s个决策树的叶子节点区域，J为其对应的叶子节点个数；fs-1（xi）为第s-1个决策树在样本i的输出值。

4）更新学习器。

式中：fs（x）为第s个决策树；I为指示函数，若输入空间x∈Rs，j，I=1，否则I=0。

5）对每个弱学习器的输出求和，得到最终的OD客流预测模型f^（x）。

3 数据来源与分析

3.1 AFC数据处理

数据来源于2020年8月份苏州市地铁AFC系统采集的刷卡数据，原始数据记录约1 800万条，其中每条刷卡数据包含一位乘客的卡号、票卡类型、进出站的日期和时间、进出车站编号，初始数据格式如表1所示。

由于工作人员日常进出维修以及数据上传中可能存在干扰数据等各类现实状况，初始数据会包含部分非自由乘客的出行数据，在进行短时OD客流集计前对这类数据进行了清洗，数据清洗后余约1 726万条。主要按照以下原则进行数据清洗：1）去除包含空值数据的行和重复行；2）去除超出运行时间范圍的数据；3）去除进出闸机时间小于1 min或大于3 h的数据。

3.2 客流特征

线网短时OD客流分布受多方面因素的影响，将相关影响因素特征与短时OD特征绑定有利于算法识别客流规律，从而提高预测的精度。本文对多种时空影响特征进行了分析。

1）天气因素 天气数据来源于国家气候数据中心，包含多种字段信息，其中如气温、气压、风向、风速以及降水量等字段记录，其上传时间间隔通常较短，易存在缺失值且缺乏真实有效的补充方式，因此选择较为完整的天气及空气质量数据作为天气影响因素，以分析不同日期天气对OD客流的影响。

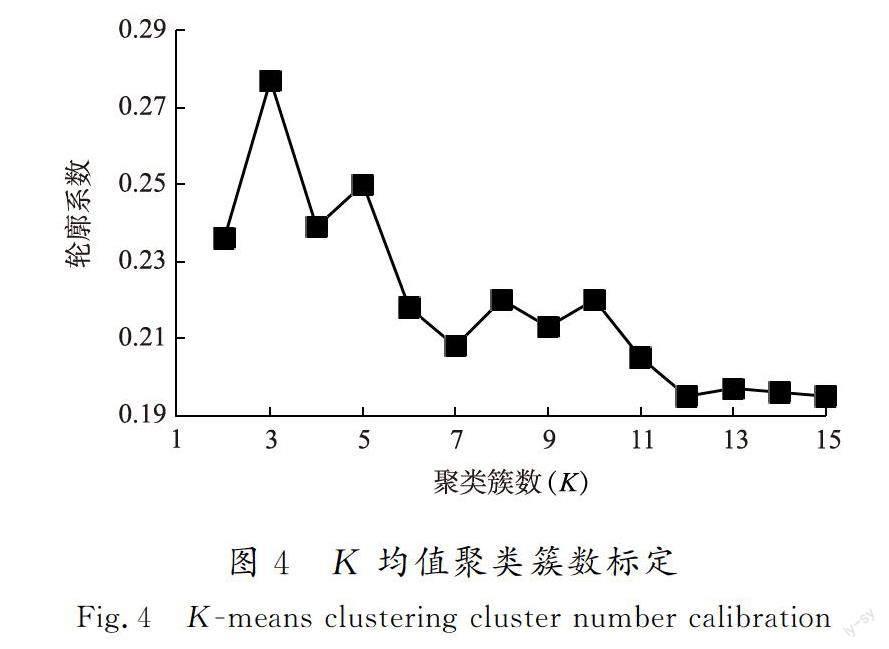
2）OD类型的标定 不同的OD因站点周围用地性质、环境影响所产生的客流趋势不同。由于峰值客流是运营管理中常用来衡量客流趋势的指标，因此将一天划分为早、晚高峰及平峰3个时段，计算各OD每天不同时段的出行比例，通过轮廓系数法确定聚类簇数，并使用K均值聚类算法进行聚类。轮廓系数是评价聚类结果好坏的一种指标，值越大说明同簇样本相距越近、不同簇样本相距越远，聚类效果越好，设置聚类簇数K取值范围为［2，15］，遍历K值并计算每一K值下的轮廓系数，如图4所示，最优聚类簇数为3，线网OD被分为3类。

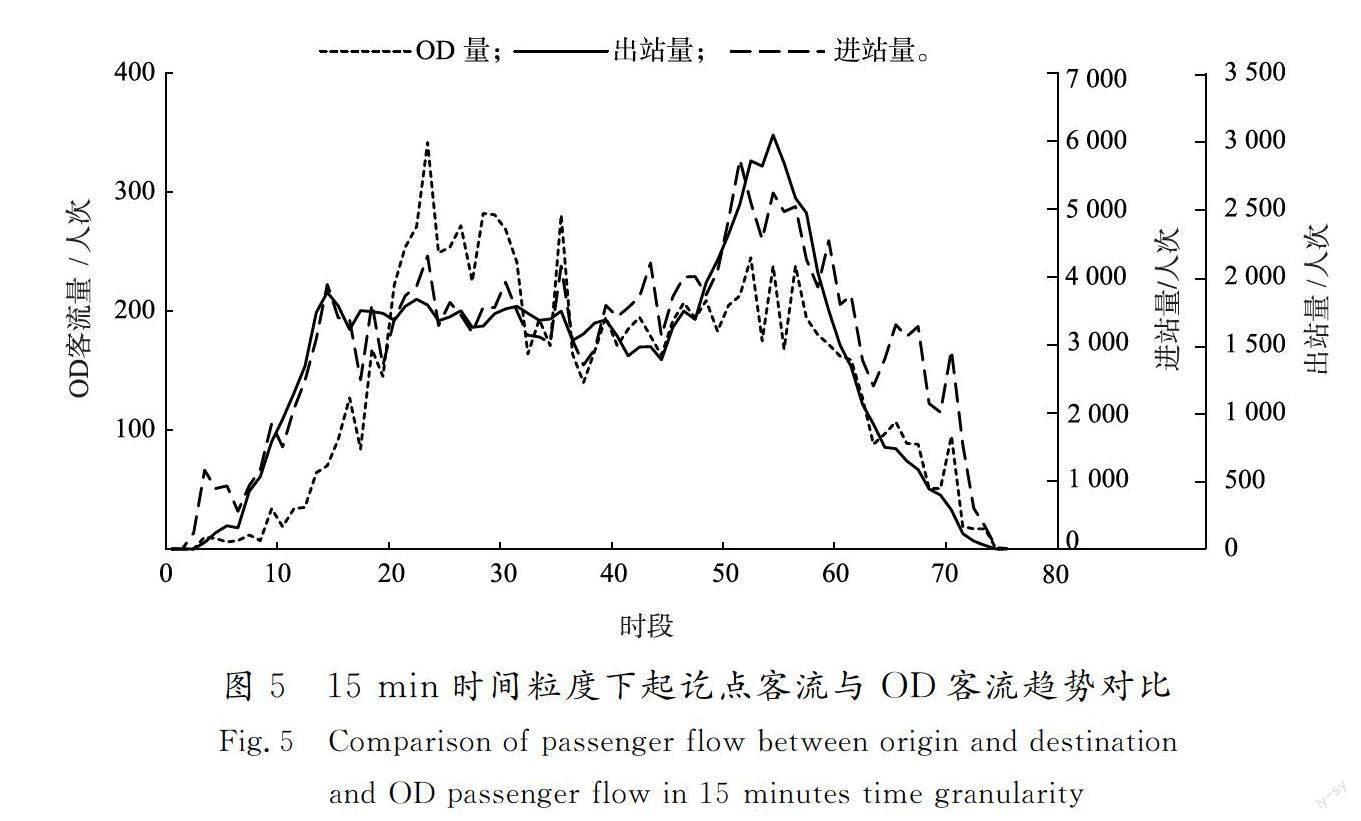
3）起讫点客流影响因素 以起讫点249～449为例绘制15 min时间粒度下某日OD量与进出站客流量趋势，如图5所示，起点进站和讫点出站客流趋势与OD客流趋势存在较强的相似性。

4）工作日与非工作日的标定 因人们出行目的的改变，客流在工作日与非工作日OD客流规律存在明显差异，通常非工作日的客流随机性更强。Pearson系数可以衡量数据的线性相关关系，系数越接近于1说明数据之间的相关性越强，因此抽样2020-08-03至2020-08-09的1周数据，使用Pearson

系数度量各时间粒度一周内每日OD客流时间序列的相似性。假设在时间粒度为Δt时该周第i天和第j天的Pearson系数为PΔt（Yi，Yj），用yti表示第i天第t个时段的OD客流量，y^ti表示在时间粒度Δt下第i天OD客流量的均值，则第i天与第j天的OD客流时间序列Yi与Yj的Pearson系数为

各时间粒度一周内每日之间的OD客流相似性如图6所示，其中2020-08-03至2020-08-07为工作日，2020-08-08至2020-08-09为周末（非工作日），由图6可以明显看出，无论在哪种时间粒度下，工作日与工作日之间的OD客流时间序列都具有较强的相似性，周六、周日之间OD客流虽然也具有较强的相似性，但相对工作日Pearson系数较低，说明非工作日时OD客流的随机性较工作日增加。同时，工作日与非工作日之间客流相似性显著降低，说明工作日与非工作日客流趋势存在明显差异。

为便于算法识别，在多源数据集融合时将各类影响因素进行特征编码，即将字符型数据转换为数值型数据，如天气特征中使用数字“1”代表晴天，“2”代表雨雪，其他字符型特征同理。以15 min时间粒度为例，最终训练数据结构及编码含义如表2所示，其中天气、空气质量、工作日和周末（非工作日）为与时间相关联的影响因素，根据日期字段与OD客流时间序列匹配; OD类别为与空间中的OD相关联的影响因素，根据进出站编号进行匹配；进出站量是与OD对应的时间段内起点车站的进站客流量和终点车站的出站客流量，分别根据进站车站编号、日期、时间和出站车站编号、日期、时间字段与OD客流时间序列匹配。

4 模型求解

4.1 评价指标

回归问题的评价指标主要是为了反映模型预测结果与实际值的拟合程度。为全面评价预测结果，选择平均绝对误差（mean absolute error， MAE）和均方根误差（root mean square error， RMSE）用于评价误差大小，R2（决定系数）用于评价预测曲线的拟合精度。

式中：ytrue为真实值；ypred为预测值；N为预测样本数。MAE反映的是真实误差，RMSE是先对误差进行平方的累加后再开方，从而放大了误差之间的差距，因此在评价中RMSE的值越小其意义越大。R2反映的是拟合优度，越接近1说明观察点在回归线附近越密集。

4.2 参数寻优

划分训练集数据为2020-08-03至2020-08-23的3周数据，测试集数据为2020-08-24至2020-08-30的1周数据，分别以15，30，60 min时间粒度执行预测。利用智能搜索框架Optuna对LightGBM模型进行参数寻优，参数寻优的目标函数即为误差评价指标RMSE，通过最小化目标函数返回不同时间粒度模型的最优参数值。参数搜索空间及不同时间粒度下的最优参数搜索结果如表3所示，其中max_depth和num_leaves共同控制树的形状，max_depth为树的深度，用于限制树的生长以防止过拟合，当时间粒度为15 min和30 min时决策树深度分别为15及20，但在时间粒度为60 min时决策树深度骤增至100，说明60 min时间粒度的模型过拟合风险较高。num_leaves为决策树的叶子节点数，配合max_depth共同使用，较大的num_leaves增加了训练集的精确度，但同样也增加了过拟合的风险。为此，寻优结果中决策树深度增加时相应叶子节点数减少，以降低过拟合风险。learning_rate为学习率，值越小意味着需要更多迭代次数，当时间粒度为30 min时学习率最大，其次是15 min和60 min，说明30 min的预测模型的时间成本应会较低。cat_smooth用于特征的概率平滑，以降低特征值中噪声数据的影响，时间粒度越大特征中噪声表现的越明显。colsample_bytree为每次迭代时对特征列的采样比例，由于构建的客流特征都与OD客流具有一定的相关性，模型偏全采样，因而受时间粒度影响较小。reg_lambda为L2正则化系数，通过对损失函数附加正则项进行惩罚减小过拟合风险，受极端值影响较大，30 min时正则化系数最小，说明30 min模型受极端值影响最小，而60 min模型受极端值影响较大。

4.3 特征重要度分析

对于模型选取的影响因素，模型训练的特征重要度如图7所示，纵坐标为特征，横坐标为该特征在树中作为划分属性的次数，代表该特征在模型构建

过程中的重要性。其中，进站车站编号和出站车站编号共同确定具体某一个OD，是决定预测结果最重要的因素。其次的影响因素是进出站量，OD客流量总是属于起讫点进出站量的一部分，一个OD出行的产生必然导致起点进站量和讫点出站量同时增长1次，两者之间存在紧密联系。OD类型、日期、时段和是否为工作日对OD客流预测也存在一定程度的影响，而天气及空气质量对预测的影响最小。

4.4 预测结果分析

为了对比算法间的预测效果差异，选取与LightGBM模型原理近似的XGBoost模型对比运算速度，选取算法原理不同的统计学原理模型，如：移动自回归模型（ARIMA）、深度学习模型（长短期记忆神经网络（LSTM）及门控循环网络（GRU）），对比预测精度。对所有模型分別进行参数调整：XGBoost和LightGBM参数类似，通过上述Optuna调参。GRU是LSTM的变体，两者都属于递归神经网络且参数相似，本文设置网络层数为4层，隐藏神经元个数为50，最大迭代次数为100，LSTM训练数据批大小为32，GRU训练数据批大小为150。ARIMA具有3个参数，在3种时间粒度下自回归项p为6/4/4，差分阶数d为0/0/0，移动平均项数q为1/3/2，最终各模型输出预测结果的误差评价指标如表4所示。

由表4可知，从预测模型上来看，LightGBM模型的预测误差在15，30，60 min时均最小，并且运算速度也最快；从预测时间粒度上看，所有模型在15 min时间粒度下预测误差最小，在30 min时间粒度下拟合优度最好。从运算速度上看，基于集成学习的LightGBM和XGBoost模型在处理海量数据，尤其是整个地铁线网的OD数据时可以达到快速收敛的效果，而深度学习模型和ARIMA模型在处理多特征的海量数据时运算速度极为缓慢。综上所述：1）对于地铁线网OD预测，LightGBM模型的精确度和运算速度都为最优，在时间粒度为15 min时，MAE为1.04，RMSE为1.69，为所有模型中最小，但拟合优度R2为0.74，相对30 min时间粒度略有不足；2）在时间粒度为30 min时，LightGBM的MAE为1.23，RMSE为2.3，而R2达到0.82，为所有模型中最好，因为随着时间粒度划分的增加，各时段集计的OD量也会增长从而放大误差，所以从整体上来看，以30 min时间粒度划分时误差项MAE，RMSE相对15 min仅略微增长，而拟合优度和时间花费达到最优，是表现最好的模型；3）在时间粒度为60 min时，各模型的误差和拟合优度表现都开始下降，是模型中最不合适做预测的时间粒度。

利用最优的LightGBM模型对2020-08-24至2020-08-30的1周数据30 min时间粒度的线网OD客流进行预测，取其中2个OD对客流预测结果的实际值和预测值进行比较，拟合效果如图8和图9所示，其中横坐标是将每天5：00～24：00按30 min时间粒度划分的时间段排序，纵坐标为OD客流量。

5 结 语

通过分析地铁线网多时间粒度的OD客流，并将多种影响因素引入到OD客流预测中，建立了基于LightGBM模型的多时间粒度线网短时OD客流预测模型，预测结果可为地铁线网的动态化运营管理提供数据支持，对改善运营质量、提高服务水平具有一定价值。

1）通过绑定不同时间粒度的OD客流序列与对应的影响因素，使LightGBM模型更好地识别客流时空分布特征并进行预测，在获取更高精度的同时也大幅提高了运算速度。对于地铁线网来说，具有高效率的LightGBM集成算法既可保证预测的时效性，又兼有较好的泛化能力拟合客流峰值曲线。

2）对于不同时间粒度的OD客流序列，预测结果存在较大差异，说明时间粒度的选择对于客流预测来说具有重要影响，所以在进行短时OD客流预测前需要预先探讨短时预测的时间粒度选择问题，不同城市的线网OD客流趋势不尽相同，最优时间粒度需要针对数据分析获得。以苏州市地铁线网为例，当使用前3周数据作为训练数据预测下一周的线网短时OD时，预测结果的误差和拟合优度在30 min时间粒度时综合表现最好。

由于缺乏历史数据，未将大型活动和节假日等特殊情况考虑在内，因此构建的模型主要适用于日常情况下的短时OD客流预测。后续研究可将特殊情况下的日期或时段进行标签化，并与常规情况进行区分，作为一个新的特征加入模型中。

参考文献/References：

［1］ 陈志杰，毛保华，柏赟，等.基于多时间尺度的城市轨道交通短时OD估计［J］.交通运输系统工程与信息，2017，17（5）：166-172.

CHEN Zhijie，MAO Baohua，BAI Yun，et al.Short-term origin-destination estimation for urban rail transit based on multiple temporal scales［J］.Journal of Transportation Systems Engineering and Information Technology，2017，17（5）：166-172.

［2］ 林友芳，尹康，党毅，等.基于时空LSTM的OD客运需求预测［J］.北京交通大学学报，2019，43（1）：114-121.

LIN Youfang，YIN Kang，DANG Yi，et al.Spatio-temporal LSTM for OD passenger demand prediction［J］.Journal of Beijing Jiaotong University，2019，43（1）：114-121.

［3］ LING Ximan，HUANG Zhiren，WANG Chengcheng，et al.Predicting subway passenger flows under different traffic conditions［J］.PLoS One，2018，13（8）：e0202707.

［4］ 张国赟，金辉.基于改进ARIMA模型的城市轨道交通短时客流预测研究［J］.计算机应用与软件，2022，39（1）：339-344.

ZHANG Guoyun，JIN Hui.Research on the prediction of short-term passenger flow of urban rail transit based on improved ARIMA model［J］.Computer Applications and Software，2022，39（1）：339-344.

［5］ 刘洋，凌力，伍元忠，等.基于约束卡尔曼滤波的城市轨道交通线网客流OD实时估计研究［J］.铁道运输与经济，2018，40（10）：103-108.

LIU Yang，LING Li，WU Yuanzhong，et al.A real-time OD estimation of passenger flow in urban rail transit network based on constrained Kalman filtering［J］.Railway Transport and Economy，2018，40（10）：103-108.

［6］ HABTEMICHAEL F G，CETIN M.Short-term traffic flow rate forecasting based on identifying similar traffic patterns［J］.Transportation Research Part C：Emerging Technologies，2016，66：61-78.

［7］ 陳通箭，袁发涛.基于支持向量机的轨道车站客流高峰期持续时间预测［J］.智能城市，2020，6（8）：10-12.

CHEN Tongjian，YUAN Fatao.Prediction of passenger flow peak duration at rail stations based on support vector machine［J］.Intelligent City，2020，6（8）：10-12.

［8］ TSAI T H，LEE C K，WEI C H.Neural network based temporal feature models for short-term railway passenger demand forecasting［J］.Expert Systems with Applications，2009，36（2 Pt.2）：3728-3736.

［9］ TIAN Yongxue，PAN Li.Predicting short-term traffic flow by long short-term memory recurrent neural network［C］//2015 IEEE International Conference on Smart City/SocialCom/SustainCom.Chengdu：IEEE，2015：153-158.

［10］CHEN Tianqi，GUESTRIN C.XGBoost：A scalable tree boosting system［C］//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.San Francisco：Association for Computing Machinery，2016：785-794.

［11］张晚笛，陈峰，王子甲，等.基于多时间粒度的地铁出行规律相似性度量［J］.铁道学报，2018，40（4）：9-17.

ZHANG Wandi，CHEN Feng，WANG Zijia，et al.Similarity measurement of metro travel rules based on multi-time granularities［J］.Journal of the China Railway Society，2018，40（4）：9-17.

［12］马超群，李培坤，朱才華，等.基于不同时间粒度的城市轨道交通短时客流预测［J］.长安大学学报（自然科学版），2020，40（3）：75-83.

MA Chaoqun，LI Peikun，ZHU Caihua，et al.Short-term passenger flow forecast of urban rail transit based on different time granularities［J］.Journal of Chang′an University （Natural Science Edition），2020，40（3）：75-83.

［13］张萍，肖为周，沈铮玺.基于长短期记忆网络的轨道交通短期OD客流量预测［J］.河北工业科技，2021，38（5）：351-356.

ZHANG Ping，XIAO Weizhou，SHEN Zhengxi.Forecast of short-term origin-destination passenger flow of rail transit based on long short-term memory network［J］.Hebei Journal of Industrial Science and Technology，2021，38（5）：351-356.

［14］韩皓，徐圣安，赵蒙.考虑线网结构的LightGBM轨道交通短时客流预测模型［J］.铁道运输与经济，2021，43（10）：109-117.

HAN Hao，XU Shengan，ZHAO Meng.LightGBM prediction model of short-term passenger flow for rail transit considering network structure［J］.Railway Transport and Economy，2021，43（10）：109-117.

［15］LI Dingzhe，PENG Jingbo，HE Dawei.Aero-engine exhaust gas temperature prediction based on LightGBM optimized by imroved bat algorithm［J］.Thermal Science，2021，25（2A）：845-858.

［16］KE Guolin，MENG Qi，FINLEY T，et al.LightGBM：A highly efficient gradient boosting decision tree［C］//Proceedings of the 31st International Conference on Neural Information Processing Systems.Long Beach：Curran Associates Incorporated，2017：3149-3157.