跳频通信中一种结合干扰预处理的平方定时同步算法

刘宇宁 王赛宇 王杨 陈敬乔 潘申富

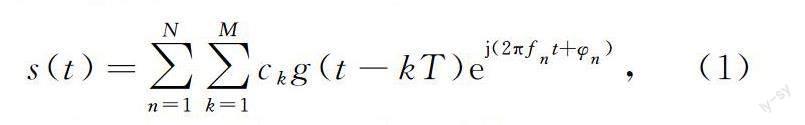
摘 要：为了提高跳频通信中定时同步算法的准确性，设计了一种结合干扰预处理的跳频信号定时同步算法。首先对解跳后信号在时域完成基于能量的自适应门限的干扰检测，并根据检测结果将受干扰信号进行置零预处理；其次对预处理后的信号采用平方法进行定时误差估计；最后根据估计结果内插完成定时恢复。结果表明，提出的改进算法选取长度为200跳的符号，在干扰相对带宽为30%、干信比为10 dB、信噪比为5 dB、时钟稳定度为1×10^-6的条件下，进行干扰预处理后定时，归一化定时误差的方差为0.000 75，满足跳频系统解调性能损失小于0.5 dB的要求。设计方法提高了干扰条件下平方法定时的准确性，在跳频通信抗干扰应用中有一定的参考价值。

关键词：无线通信技术；跳频通信；干扰检测；定时同步;误差

中图分类号：TN927+.21

文献标识码：A

DOI： 10.7535/hbgykj.2023yx02009

A square timing synchronization algorithm combined with interference preprocessing in frequency hopping communication

LIU Yuning1， WANG Saiyu2， WANG Yang1， CHEN Jingqiao1， PAN Shenfu1

（1.The 54th Research Institute of China Electronics Technology Group Corporation （CETC）， Shijiazhuang，Hebei 050081， China;

2.The 10th Research Institute of China Electronics Technology Group Corporation（CETC）， Chengdu，Sichuan 610036， China）

Abstract：In order to improve the accuracy of timing synchronization algorithm in FH communication， a timing synchronization algorithm of FH signal combined with interference preprocessing was designed. Firstly， the interference detection based on the adaptive threshold of energy was completed in the time domain， and the interfered signal was preprocessed according to the detection results. Secondly， the square method was used to estimate the timing error of the pretreated signal. Finally， the timing recovery was completed by interpolation according to the estimation results. The results show that the proposed improved algorithm selects symbols with a length of 200 hops is timed after interference preprocessing， with the relative interference bandwidth of 30%， the signal to interference ratio of 10 dB， the signal to noise ratio of 5 dB， and the clock stability of 1×10^-6， and the variance of normalized timing error is 0.000 75， which meets the requirement that the demodulation performance loss of frequency hopping system is less than 0.5 dB. The design method improves the accuracy of squared timing under interference conditions， and has certain reference value in the application of frequency hopping communication anti-interference.

Keywords：wireless communication technique; frequency hopping communication; interference detection; timing synchronization；error

跳頻（frequency hopping，FH）通信是现代通信领域中一种有效抗干扰手段，在军用和民用领域都得到了越来越广泛的应用^［1］。要保证系统在干扰条件下准确接收数据，符号定时同步的抗干扰性能至关重要。

跳频系统的定时同步算法可分为反馈算法^［2-5］和前馈算法^［6-8］。在干扰条件下应用跳频系统时，定时同步算法的性能至关重要。现有抗干扰定时同步算法针对OFDM系统^［9-12］特点展开设计，不适用于跳频系统。目前缺乏对跳频系统在干扰条件下的定时性能研究，需要设计具有良好抗干扰能力的定时同步算法，保证跳频系统抗干扰应用。

受干扰的跳频信号如图1所示。跳频信号受部分频带干扰时，表现为个别跳的跳频周期受到了干扰。如果在符号定时过程中使用受干扰跳的数据，会导致定时误差增大，引起系统解调性能损失。因此，定时同步算法抗干扰改进的目的是去除受干扰跳，提取无干扰跳完成定时估计，减小定时误差导致的系统解调性能损失。

针对上述问题，本文基于数字平方滤波^［7］定时算法，提出了一种改进的抗干扰定时同步算法。改进算法使用合适的定时同步符号长度，在时域进行基于能量的干扰检测，检测门限具有自适应的特点，提高了定时同步的抗干扰性能，保证了系统接收数据的准确性，使得符号定时引起的解调损失在0.5 dB以内。

1 系统模型

本文针对跳频抗干扰系统，采用π/4-DBPSK调制，脉冲成形和匹配滤波均采用根升余弦滤波器，降低非理想信道的码间串扰。系统模型如图2所示。

对于跳频系统已调信号进行上变频时，载波频率受伪随机序列控制，不同跳频周期使用不同的载波频率。跳频后N跳信号可表示为式（1）：

式中：ck为信号源符号映射之后数据，k=1，2，…，M；M为跳频周期传输符号数； n=1，2，…，N；N为跳频周期数；fn为第n跳的载波频率；φn为第n跳载波的初始相位。频率值受伪随机序列控制，在跳频频点集合内跳变，频点切换时，相邻两跳之间载波相位很难保证连续。

s（t）在接收端接收到的信号可表示为式（2）：

式中：n（t）为噪声；J（t）为干扰。跳频同步后，接收端匹配滤波器输出信号y（t）可表示为式（3）：

式中：τk为信道传输过程中引入的随机定时误差；n′（t）为下变频之后的高斯白噪声。符号定时恢复的作用就是估计该随机定时误差，恢复理想的采样时刻。

跳频系统应用场景中干扰相对带宽为30%；对于受干扰部分的跳频周期，干信比（JSR）范围为10～60 dB。跳频系统使用的时钟稳定度为1×10^-6，每个跳频周期符号数为16。

2 定时对系统解调性能的影响

为了减小跳频系统的解调性能损失，在设计抗干扰定时同步算法前，需要研究定时误差对误码性能的影响，并分析干扰条件下的定时性能。

2.1 定时误差与解调误码性能

反馈定时同步算法，如Gardner位定时误差提取算法^［2］、超前滞后支路位同步法^［3］等通过闭环调整实现位同步，需要利用较长的连续数据。平方定时同步算法适应多种调制方式，并且独立于载波相位。根据跳频系统跳频周期内符号数少、相邻两跳之间载波相位不能保证连续的特点，选择平方定时同步算法进行定时误差估计，再利用估计结果进行内插恢复。

对解跳后的连续信号进行N倍采样后，得到离散信号y（n），对信号进行平方，计算LN点FFT，提取FFT后对应1/T频点的谱分量，组成的傅里叶变换序列为式（4）：

在高斯白噪声信道下，Y的归一化相位值是定时误差τ的无偏估计，即：

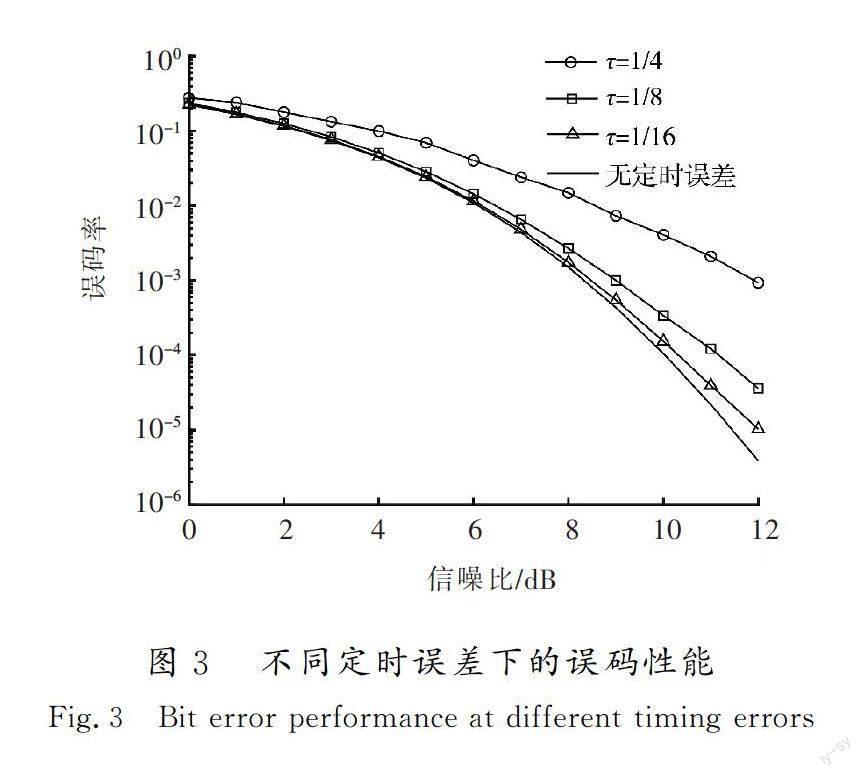
定时误差τ的大小会影响解调性能，图3给出了不同定时误差情况下的解调性能，随着信噪比的增加，符号间串扰功率与噪声功率的比值也增加，符号定时误差对解调性能的损失扩大。

由图3可得表1中的对应关系，当归一化定时误差的方差小于0.003 91时，符号定时误差对解调性能的损失在0.5 dB以内。

理想条件下，对于平方定时同步算法，随着使用定时符号数L的增加，意味着观察时间范围增大，对应频域的频率分辨率提升，则定时误差估计的精确度也随之提高。图4为使用不同长度数据进行定时误差估计的归一化定时误差的方差，可以看出在使用数据符号长度L>96时，归一化定时误差的方差一直控制在0.003 91以内，保证了符号定时误差对解调性能的损失在0.5 dB以内。

工程实践中，受接收端时钟稳定度限制，数据长度不能无限长，使用超出最佳观测长度的数据反而会导致系统性能下降，在信噪比为5 dB时，最佳观测长度L为2 000^［13］。

2.2 干扰下的定时性能

接收有干扰的信号进行平方后，根据高斯白噪声与有用信号和干扰信号不相关的特点，根据式（4）得到式（5）：

式中：P0（·）为有用信号频谱自卷积；J（·）为干扰频谱自卷积；PJ（·）为有用信号和干扰信号频谱的互卷积。当不存在干扰时，J（·）和PJ（·）等于0，有用信号频谱自卷积P0（·）幅角为0，因此在没有干扰时才能对定时误差进行准确估计；在干扰存在时3项累加后幅角不为0，因此Y的归一化相位值不能准确反映定时误差τ。

根据最佳观测长度以及系统干扰相对带宽，选取数据符号长度L=3 200，图5和图6分别为相同条件下，不同干扰强度和不同干扰相对带宽下，归一化定时误差的方差与信噪比之间的关系。由图5可得：在JSR>20 dB条件下，归一化定时误差的方差大于0.003 91，导致解调性能损失大于0.5 dB。

图6给出在不同干扰相对带宽占比的定时性能，可见：当干扰相对带宽为20%时，归一化定時误差的方差大于0.015 6，定时估计误差导致解调性能损失大于1 dB；当干扰相对带宽大于5%时，归一化定时误差的方差大于0.003 91，定时估计误差导致解调性能损失大于0.5 dB。

从图5和图6可以看出，当存在干扰时，会对定时同步性能产生影响，极端条件下，会严重影响系统定时同步性能，因此，非常有必要提升定时同步算法的抗干扰性能。

3 抗干扰定时同步算法

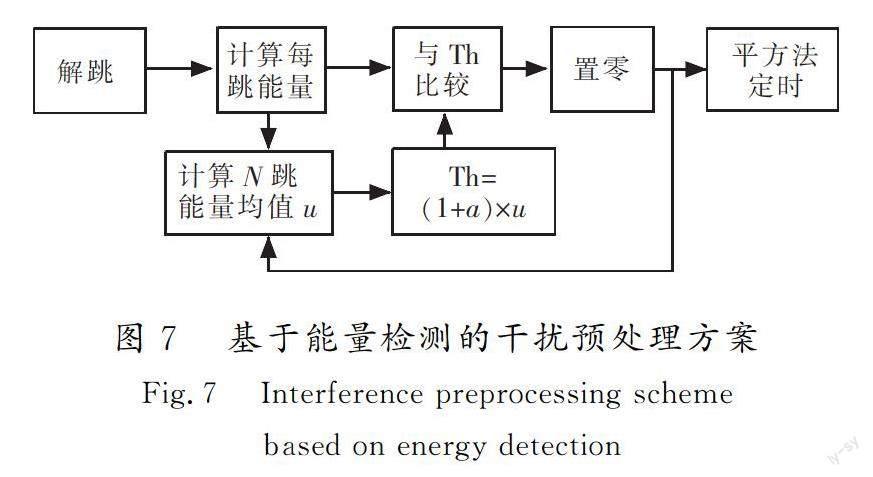
为了优化干扰条件下的符号定时效果，抗干扰定时同步算法根据干扰检测结果，将受干扰跳信号置零，利用未受干扰部分完成定时同步。干扰检测门限计算基于连续均值去除算法^［14-15］，将每跳能量作为检测统计量，根据能量均值更新干扰检测门限Th。

干扰预处理方案如图7所示。

对于跳频系统，干扰使得一部分跳频周期内信号受到干扰，解跳后可以從时域角度以跳频周期为单位进行干扰检测。根据式（2）解跳后第n跳信号为式（6）：

r（n）=s（n）+n（n）+βnJ（n） ，（6）

式中：βn为0或1，表示第n跳是否存在干扰；信号s（n）的平均功率为σ2s；n（n）为高斯白噪声，均值为0，方差为σ20；J（n）的平均功率为σ2J。

在完成解跳的前提下，跳周期内信号幅值可以表示为式（7）：

A（n）=|r（n）|， n=1，2，…，N。（7）

由于信号和背景噪声不相干，当接收信号中存在干扰时，σ2J/（σ20+σ2s）＞＞1，幅值A近似服从于高斯分布^［16］，如式（8）所示：

当接收信号中不存在干扰时，σ2J/（σ20+σ2s）＜＜1，其概率密度函数为式（9）：

迭代过程中，第1步假设没有受到跳干扰，根据没有干扰时的概率密度函数式（9）可得分布函数F（A），当设定一定的检测概率Pt时，门限因子可表示为式（10）^［16］：

根据式（10），门限因子a由检测概率Pt决定，与噪声方差无关。实际应用中，检测概率在90%～99.9%时门限因子a的取值范围为0.5～1.5^［16］。门限设置是检测算法的核心问题。检测门限由多个跳频周期内信号幅值的均值与门限因子相乘，再通过迭代更新得到，根据检测结果将受干扰跳信号幅度置零处理后，再进行平方定时估计。

用m表示迭代次数，每次迭代中，受干扰跳集合为Jm，未受干扰跳集合为Im，未受干扰跳能量和为Am，未受干扰跳数为Nm，共有N跳，算法流程如下。

1）初始设m=1，Jm为空集，Im={1，2，…，N}，此时认为接收所有跳中不存在受干扰跳，Am=∑n∈ImA（n），Nm=size（Im）。

2）检测门限Th=（1+a）Am/Nm，将每跳信号能量幅值与检测门限比较，若大于门限则判定这一跳为受干扰跳，跳内所有样点置零，不作为定时依据，根据判断计算集合Jm+1和Im+1。

3）更新未受干扰信号能量和Am+1，未受干扰跳数Nm+1。

4）当判定受干扰跳集合Jm为空集或者算法达到迭代次数上限时，跳转至第5）步；否则令m=m+1，跳转至第2）步继续循环。

5）假设总共迭代了P次，则最终的干扰跳集合J=J1∪J2∪…∪JP。

4 仿真分析

抗干扰定时同步算法目的在于优化定时效果，因此干扰检测在参数选择时需要考虑定时算法要求。为了保证检测后符号数仍满足定时要求，一次检测跳数N为200，设定虚警概率为1%；为保证收敛，迭代次数为10^［17］。

使用基于能量检测的干扰预处理方案和跳频系统模型，假设干扰相对带宽为30%，在此条件下，图8为使用干扰检测算法后的检测效果仿真图。

由图8可以看出，在不同干信比条件下，检测概率不同，对于定时同步算法而言，在JSR=10 dB时检测概率Pt接近于1，意味着用于定时同步的数据为未受干扰部分。

表2为JSR=10 dB时，不同干扰带宽下的检测概率，可以看出，随着干扰带宽的增加，检测概率有所下降，但是干扰检测概率仍接近1，系统定时性能不受干扰影响。

跳频抗干扰典型应用场景中的JSR为10～60 dB，当JSR大于10 dB时，干扰检测概率接近1，系统定时性能不受干扰影响。图8中JSR=-5 dB，检测概率较低，但如图9所示，当干信比较低时干扰对定时性能产生影响较小。结果表明，虽然低干信比条件下检测概率较低，但是定时误差仍能满足系统要求。

目前对定时同步算法抗干扰性能的研究比较少，文献［18］提出的基于线性相位近似的最大似然估计定时同步算法具有一定的抗干扰特性，因此这里选择此算法作为对照。在JSR=10 dB、信噪比Eb/N0为5 dB时，各方法的归一化定时误差的方差如表3所示。使用干扰检测算法后，归一化定时误差的方差小于0.003 91。根据表1可知，符号定时误差导致的解调性能的损失小于0.5 dB，最大似然算法定时性能满足要求，但是改进算法定时性能更好。

图10为使用干扰检测算法后的不同干扰相对带宽下的定时同步效果，从仿真结果可以看出，使用干扰检测算法后，归一化定时误差的方差均控制在0.003 91内，满足解调性能的要求。

由于门限值的更新与门限因子相关，因此需要考虑干扰检测门限参数选择对定时同步性能的影响。图11为相同干扰条件下，使用不同门限参数的定时同步效果，可以得出门限因子a应选择1.5，门限的设置与检测概率相关，选择越大的门限因子对应检测概率越高，检测性能更好，进而定时性能更好，仿真结果与理论分析相符。

5 结 语

针对跳频通信干扰应用场景下符号定时性能损失的问题，本文提出了具有优良抗干扰能力的定时同步算法，改善了系统解调性能，保证了跳频系统抗干扰应用。首先，分析了定时误差与系统误码性能的关系，得出定时误差控制在0.003 91以内时解调性能损失小于0.5 dB。其次，在研究干扰对定时性能影响的基础上，设计了以跳为单位去除干扰的定时同步算法。算法针对跳频系统特点进行设计，在高强度干扰和干扰带宽占比较大时均取得了较好的定时结果，且相较其他算法定时性能更好。

所提方法在大干信比干扰条件下具有较好的效果，而当干信比较小时，其带来的定时性能提升受限。因此，如何在低干信比条件下取得更好的效果，是未来进一步研究的方向。

参考文献/References：

［1］ 常海锐，王峰.防空导弹武器系统无线通信抗干扰能力分析［J］.现代防御技术，2020，48（6）：60-66.

CHANG Hairui，WANG Feng.Analysis on antijamming ability of wireless communication of air defense missile weapon system［J］.Modern Defence Technology，2020，48（6）：60-66.

［2］ GARDNER F M.Demodulator Reference Recovery Techniques Suited for Digital Implementation［R］. Brussels：European Space Agency， 1988.

［3］ 潘煒程.跳频电台调制解调技术的研究与实现［D］.南京：南京理工大学，2018.

PAN Weicheng.Research and Implementation of Frequency Hopping Radio Modulation and Demodulation Technology［D］.Nanjing：Nanjing University of Technology，2018.

［4］ 岳海啸，廉保旺，曹娜.高速跳频通信系统中快速位同步的研究和实现［J］.弹箭与制导学报，2006（sup3）：626-628.

YUE Haixiao，LIAN Baowang，CAO Na.Research and realization of fast bit synchronization in high speed frequency-hop communication system［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2006（sup3）：626-628.

［5］ 陈安旭.Link 16数据链物理层关键技术的研究与验证［D］.成都：电子科技大学，2020.

CHEN Anxu.Research and Verification of Key Technologies in Link 16 Data Link Physical Layer［D］.Chengdu：University of Electronic Science and Technology of China，2020.

［6］ 王琛，王芳，李明齐.无线自组织通信中基于前导符号的定时同步［J］.系统工程与电子技术，2020，42（6）：1372-1378.

WANG Chen，WANG Fang，LI Mingqi.Timing synchronization for wireless ad hoc communication based on preamble symbol［J］.Systems Engineering and Electronics，2020，42（6）：1372-1378.

［7］ OERDER M，MEYR H.Digital filter and square timing recovery［J］.IEEE Transactions on Communications，1988，36（5）：605-612.

［8］ 邓军.全数字接收机码元同步算法的VLSI实现研究［D］.西安：西安电子科技大学，2011.

DENG Jun.Study on VLSI Implementation of Symbol Synchronization for All Digital Receiver［D］.Xi′an：Xidian University，2011.

［9］ 张秀艳，高岩.OFDM系统改进的定时同步算法［J］.信息技术，2020，44（12）：77-81.

ZHANG Xiuyan，GAO Yan.OFDM timing synchronization algorithm based on CAZAC sequence［J］.Information Technology，2020，44（12）：77-81.

［10］申敏，毛文俊，袁一铭，等.基于MIMO电力线信道的定时同步算法［J］.光通信研究，2022（2）：18-21.

SHEN Min，MAO Wenjun，YUAN Yiming，et al.Timing synchronization method in MIMO power line channel communications［J］.Study on Optical Communications，2022（2）：18-21.

［11］张娜.宽带卫星通信系统中FH-OFDM同步技术研究［D］.沈阳：沈阳理工大学，2016.

ZHANG Na.Research on FH-OFDM Synchronization Technology in Broadband Satellite Communication System［D］.Shenyang：Shenyang Ligong University，2016.

［12］张雪坤，别红霞，郑健，等.一种抗窄带干扰的OFDM符号定时同步改进算法［J］.北京邮电大学学报，2015，38（1）：76-81.

ZHANG Xuekun，BIE Hongxia，ZHENG Jian，et al.Improved symbol timing synchronization algorithm for OFDM systems mitigating narrowband interference［J］.Journal of Beijing University of Posts and Telecommunications，2015，38（1）：76-81.

［13］潘申富.基于频带共享的卫星通信关键技术研究［D］.北京：北京大学，2003.

PAN Shenfu.Research on Key Technologies of Satellite Communication Based on Band Sharing［D］.Beijing：Peking University，2003.

［14］SAARNISAARI H.Consecutive mean excision algorithms in narrowband or short time interference mitigation［C］//

IEEE Position Location and Navigation Symposium.Monterey：IEEE，2004：447-454.

［15］朱付强，陈亚丁，袁东华.一种基于CME的改进型干扰信号检测算法［J］.通信对抗，2017，36（3）：10-14.

ZHU Fuqiang，CHEN Yading，YUAN Donghua.An improved jamming signal detection algorithm based on CME algorithm［J］.Communication Countermeasures，2017，36（3）：10-14.

［16］张天林.基于信号能量的干扰检测技术研究［D］.重庆：重庆大学，2018.

ZHANG Tianlin.Study on Interference Detection Technology Based on Signal Energy［D］.Chongqing：Chongqing Univer-sity，2018.

［17］徐卓异，王兵.一种基于频谱估计的跳频系统干扰检测算法［J］.电子设计工程，2013，21（24）：138-141.

XU Zhuoyi，WANG Bing.An interference detection algorithm based on spectrum estimation for the frequency-hopping system［J］.Electronic Design Engineering，2013，21（24）：138-141.

［18］王樂，刘靖.基于线性相位近似的SOQPSK-TG信号同步算法［J］.电讯技术，2021，61（3）：348-352.

WANG Le，LIU Jing.SOQPSK-TG signal synchronization based on linear phase approximation［J］.Telecommunication Engineering，2021，61（3）：348-352.