介电高弹聚合物运动轨迹跟踪控制研究

王超隆 杨熙鑫 官源林

摘要：针对介电高弹聚合物的轨迹跟踪控制问题，本文提出自适应径向基函数（radial basis function，RBF）神经网络滑模控制（sliding mode control，SMC）算法，实现了对介电高弹聚合物运动轨迹的跟踪控制。首先考虑超弹性和粘黏性等引起动力学模型中的未知项，外界干扰导致模型的不确定性，利用RBF神经网络的任意逼近连续函数特性、滑模控制的鲁棒性和自适应控制在线调整控制率设计控制器，并构造Lyapunov函数，证明控制器的稳定性，实现了对介电聚合物轨迹跟踪控制，结果显示聚合物的位置跟踪极值误差小于1%，响应时间约为0.7 s，表明系统具有较高的动态性能，实现了结构的线性运动轨迹跟踪。同时，分析了激励频率和宽度预拉伸比对结构跟踪轨迹的影响规律，设计了系数参数的优化方法。研究结果表明，该控制器提高了轨迹跟踪的精确度，验证了所提控制系统具有较强的自适应性、稳定性及优化方法的有效性。该研究为软体机器人的仿生驱动与轨迹跟踪控制提供了理论依据。

关键词：介电高弹聚合物； 超弹性； 粘弹性； RBF神经网络； 滑模控制

中图分类号： TP13; TP183

文献标识码：A

文章编号：1006-9798（2023）02-0046-07； DOI：10.13306/j.1006-9798.2023.02.007

基金項目：山东省自然科学基金资助项目（ZR2019PEE018，ZR2020QE158）；山东省科技型中小企业创新能力提升资助项目（2021TSGC1063）

作者简介：王超隆（1990-），男，硕士研究生，主要研究方向为介电高弹聚合物的驱动与控制。

通信作者：杨熙鑫（1984-），女，博士，副教授，主要研究方向为介电高弹聚合物的仿生驱动与控制。 Email：yangxixin@qdu.edu.cn

随着科学技术的发展进步，智能软体材料得到了广泛应用。基于智能软体材料的软体机器人引起人们关注，与传统刚性机器人相比，它具有更好的灵活性、生物亲和性及环境适应性。介电高弹聚合物作为软体机器人常用的驱动材料之一，具有响应速度快、驱动位移大和能量密度高等特点，在软体机器人领域具有广阔的应用前景［1-3］。然而其超弹和粘弹等特点可导致介电高弹聚合物数学模型的非线性强，对运动轨迹的线性跟踪控制研究极具挑战。近年来，许多研究者从材料［4-6］和力学分析［7-8］方面，对介电高弹聚合物开展了相关研究，建立相应的数学模型，但通过模型获得材料的运动响应存在强非线性，其运动控制理论引起广泛关注。ZHANG R等人［9］提出标准的闭环比例、积分和微分（proportional，integral and differential，PID）控制；王红红等人［10］提出了模糊控制和滑模控制方法，但这些控制方法在控制介电高弹聚合物的非线性动态方面效果较差。为克服PID固有的局限性，G.RIZZELLO等人［11-12］提出了PID和非线性补偿的整合方法，实现了运动轨迹控制，但该方法未考虑粘弹性。针对材料的粘弹性，徐健等人［13］提出了天牛须搜索（beetle antennae search，BAS）算法，优化PID的控制方法，实现对软体机器人的精准控制，但该算法未考虑抗干扰能力，跟踪误差较大；CHEN H Q等人［14］针对介电弹性体致动器具有较大的变形能力和环境兼容性，建立了有界和无界最优控制策略，通过实时调节施加的电压，抑制平衡位置周围的随机振动；程林云等人［15］提出一种基于径向基函数神经网络的自适应控制方法，提高了跟踪精度、抗干扰能力和鲁棒性，然而运行时间较长，增加了运动轨迹的响应时间；王亚午等人［16］提出扰动抑制的自适应轨迹跟踪控制策略，实现介电高弹聚合物的跟踪控制目标，但未考虑粘黏性对运动跟踪轨迹的影响；JIANG Z等人［17］考虑弹性体固有的粘弹性和非线性，设计了基于相对蠕变模型的蠕变补偿器以消除蠕变，开发了一种基于零振动输入整形技术的振动补偿器，以抑制蠕变补偿弹性体的振动动力学；LI Y L等人［18］基于搭建的动态方程，提出闭环反馈控制算法，但未考虑频率变化的影响；樊亚玲等人［19］结合等双轴预拉伸情况下系统的状态方程，分析不同预拉伸比下极限电致应变、电场强度和电位移等参数关系，获取该介电高弹聚合物的运动稳态工作区间。基于此，本文结合介电高弹聚合物粘弹性的非线性动力学模型，提出一种基于RBF神经网络的自适应滑模控制方法，实现对介电高弹聚合物线性运动轨迹的跟踪控制。该研究为实现介电高弹聚合物驱动软体机器人的应用奠定了理论基础。

1 问题描述

1.1 动态模型

为研究介电高弹聚合物的非线性运动与主动控制，本文设计了基于软体与刚性材料相结合的介电高弹结构［20］。介电高弹聚合物结构示意图如图1所示。

由图1a可知，介电高弹聚合物具有不可压缩性，设L1、L2 和L3分别为初始状态下材料的长度、宽度和厚度，ρ为密度，材料因超弹性具有电致大变形的优良性。为提高材料的运动性能，需对材料进行预拉伸。图1b中，λ1～λ3为聚合物在方向1～3上预拉伸长度、宽度和厚度的变形比，获得拉伸后，长度、宽度和厚度分别为λ1L1 、λ2L2 和λ3L3 。为了确保材料处于纯剪切状态，利用刚性框架限制2个方向变形。假设结构弹簧刚度为k，棒子质量为m，电位移表示为

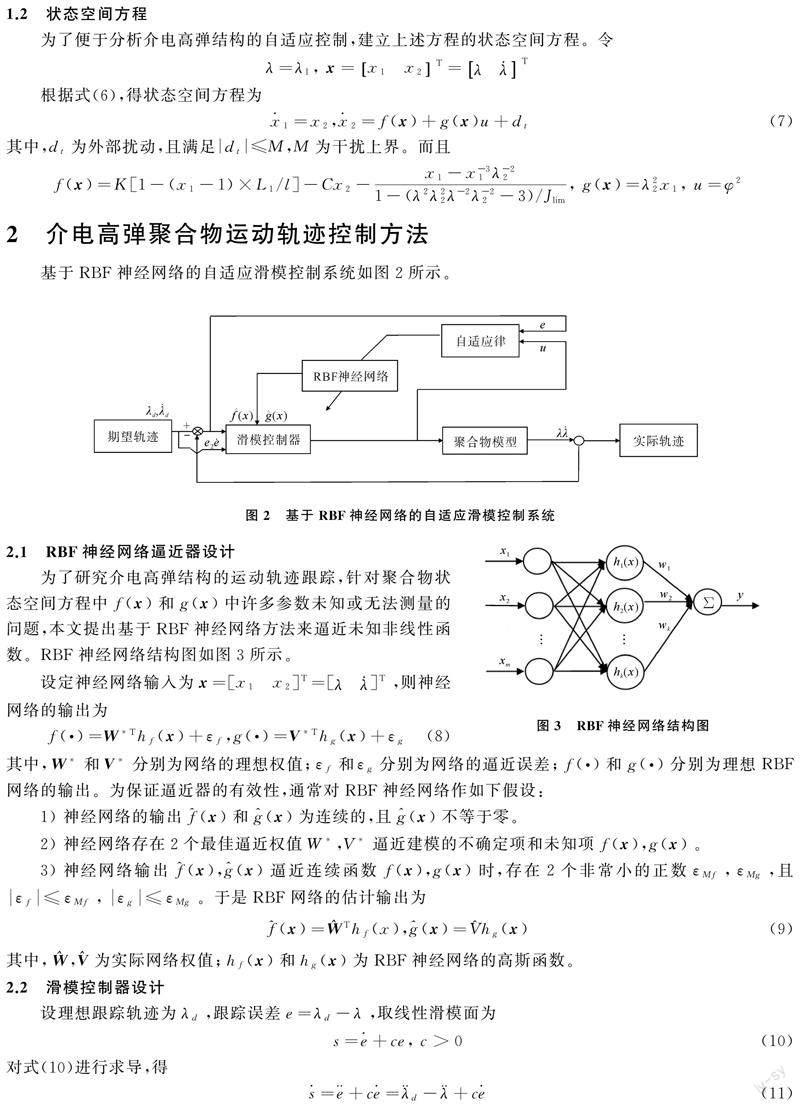
2 介电高弹聚合物运动轨迹控制方法

基于RBF神经网络的自适应滑模控制系统如图2所示。

2.1 RBF神经网络逼近器设计

为了研究介电高弹结构的运动轨迹跟踪，针对聚合物状态空间方程中f（x）和g（x）中许多参数未知或无法测量的问题，本文提出基于RBF神经网络方法来逼近未知非线性函数。RBF神经网络结构图如图3所示。

3 仿真实验

3.1 聚合物非线性运动轨迹

为了验证所提自适应控制方法的有效性和稳定性，本研究在Maltab上对控制模型进行仿真分析。设计初始条件x0=［pi/600］，目标轨迹为标准正弦信号，滑模面系数c=14，介电高弹结构的模型参数如表1所示。

在1 Hz标准激励频率下，给出介电高弹结构的期望轨迹与未加控制的实际运动轨迹，聚合物位置轨迹跟踪随时间变化曲线如图4所示。图中，红色曲线为介电高弹聚合物的目标轨迹，黑色虚线为系统的实际响应曲线。由图4可以看出，因聚合物具有超弹性，使其运动轨迹呈现出非线性和不可控性，实际轨迹上、下波动较大，实际运动频率与目标频率不一致，与目标运动轨迹差距较大。为了更好的跟踪目标轨迹，需要引入控制器来消除或减少系统的超弹性影响，实现对介电高弹聚合物的运动轨迹高精度跟踪。

3.2 基于RBF神经网络滑模控制聚合物运动轨迹

在1 Hz标准激励频率下，介电高弹结构的运动轨迹跟踪响应误差，聚合物误差随时间变化曲线如图5所示。图中，红色曲线为期望运动轨迹，黑色虚线为实际运动轨迹，图5a为两者轨迹之差。

由图5可以看出，该控制方法能够实现介电高弹结构按照期望的渐进跟踪，文献［17］中极值误差為1.76%，响应时间为1.2 s（跟踪误差达到稳态时间），与其相比，本文方法所得极值误差约为1%，响应时间约为0.7 s，具有更好的动态特性。该研究提高了轨迹跟踪的精确度，无需设计观测器，避免了计算量，验证了所提方法的有效性。

3.3 不同运动频率下轨迹跟踪控制

为了研究运动频率对介电高弹结构的运动轨迹影响，结合上述参数，选用5种不同的低频激励信号（频率分别为1 ，1.5，2 ，2.5和3 Hz），分析结构轨迹运动曲线及其误差，在不同频率下，聚合物位置跟踪和误差随时间变化曲线如图6所示。由图6可以看出，该控制方法能够实现结构的线性运动轨迹跟踪，但随着频率的线性增大，运动轨迹极值误差逐渐增加，由0.01～0.15，响应时间逐渐变长，由0.7～4.7 s。

为了减少频率变化对极值误差和响应时间的影响，研究滑模系数c对运动轨迹跟踪的影响规律。滑模系数调节前后极值误差与响应时间如表2所示。由表2可以看出，随着频率的线性增加，调整滑模系数也线性增加，结构运动轨迹曲线的极值误差和响应时间大幅度降低，动态性能获得极大的改善。调整后，在运动频率为3.0 Hz时，最大误差较调整前减少92.7%，调整时间减少了80.9%。说明通过改变滑模系数，能够有效调节聚合物运动的动态性能，提高控制方法的鲁棒性。

为了更直观地观察调整滑模系数对运动轨迹的影响结果，本研究通过柱状图进行分析，滑模系数对运动轨迹的极值误差与响应时间影响结果如图7所示。在其他条件不变及激励频率小范围线性增加下，系统动态性能指标逐渐增大，调整滑模系数c之后，系统的极值误差和响应时间大幅度减小，证明参数优化能够改善结构动态性能，提高聚合物轨迹跟踪的精准性。

3.4 不同宽度伸缩比下运动轨迹跟踪控制

为了研究结构参数对运动轨迹控制方法的稳定性影响，分析不同宽度伸缩比λ2对结构运动轨迹曲线的影响。在λ2线性变化下，不同宽度伸缩比的运动轨迹曲线和误差如图8所示。由图8可以看出，所有曲线的最大误差约为0.01，调整时间均接近0.7 s，说明改变宽度伸缩比λ2对聚合物运动轨迹跟踪控制没有太大影响，证明控制方法具有较强的自适应性和稳定性。

4 结束语

本文提出了一种自适应RBF神经网络滑模控制方法，实现对聚合物轨迹跟踪控制。仿真结果表明，在标准激励频率下，跟踪曲线具有较好的动态性能指标，验证了所提方法的简洁性和有效性。在不同激励频率下，随着频率的增大，动态性能逐渐变差，运用所提参数的优化方法，能够大幅度提高结构的性能。不同宽度预拉伸比下系统运动轨迹表明，系统不受宽度预拉伸比变化的影响，说明所提方法具有较强的自适应性和鲁棒性。本文控制方法为聚合物广泛应用提供了思路和方法，为软体机器人的仿生驱动与控制研究提供理论依据，具有一定的应用价值。由于所提控制器的趋近律为一般趋近律，会造成运动曲线在平衡点附近发生抖震现象，后续会继续研究减少或消除该现象，由于线性滑模面收敛较缓慢，增加了响应时间，接下来会考虑用其他滑模面进行仿真探究。

参考文献：

［1］ KOFOD G，WIRGES W，PAAJANEN M，et al. Energy minimization for self-organized structure formation and actuation［J］. Applied Physics Letters，2007，90（8）：108916.

［2］ CHEN Z，UM T I，BART-SMITH H. A novel fabrication of ionic polymer-metal composite membrane actuator capable of 3-dimensional kinematic motions［J］. Sensors and Actuators，2011，168（1）：131-139.

［3］ TIAN L，GAO L，YU L，et al. Fast-moving soft electronic fish［J］. Science Advances，2017，3（4）：1-8.

［4］ 徐婷婷，刘茜，陶世嘉，等. 炭黑/硅橡胶介电弹性体复合材料的制备研究［J］. 高分子通报，2021，5（5）：96-101.

［5］ 程文露，曹江勇，刘洪福，等. 介电弹性体智材料的应用能［J］. 弹性体，32（5）：91-97.

［6］ 刘志运，江泽华. 介电弹性体材料的研究综述［J］. 机电工程技术，2022，51（5）：51-55.

［7］ 程阳，曹杰，王营博，等. 介电弹性体驱动液体透镜的设计与分析［J］. 光学学报，2021，20（5）：158-167.

［8］ 孙杰，赵娟，卢凯文. 介电弹性体驱动材料力电特性研究［J］. 现代电子技术，2022，45（15）：7-14.

［9］ ZHANG R，IRAVANI P，KEOGH P. Closed loop control of force operation in a novel self-sensing dielectric elastomer actuator［J］. Sensors Actuators，2017，264：123-132.

［10］ 王红红，杜敬利，保宏. 软体机器人控制策略［J］. 机器人，2020，42（5）：626-641.

［11］ RIZZELLO G，NASO D，YORK A，et al. Model-based PID control of a dielectric electro-active polymer positioning system［J］. IFAC Proc，2014，47（11）：10926-10933.

［12］ RIZZELLO G，NASO D，SEELECKE S，et al. Modeling identification and control of a dielectric electro-active polymer positioning system［J］. Control System Technology，2014，23（6）：632-643.

［13］ 徐健，惠楠，苏泽斌. 基于BAS-PID算法的介电弹性体执行器控制研究［J］. 西安工程大学学报，2021，35（4）：84-89.

［14］ CHEN H Q，WANG Y，JIN X L，et al. Random vibration control for multi-degree-of-freedom mechanical systems with soft actuators［J］. International Journal of Non-Linear Mechanics，2019，113（7）：44-54.

［15］ 程林云，张雷，宋晓娜. 基于RBF神经网络的机械臂自适应控制方法［J］. 计算机测量与控制，2019，27（7）：79-84.

［16］ 王亚午，叶雯珺，张一龙，等. 基于介电弹性体驱动器的软体机器人建模与跟踪控制［J］. 控制理论与应用，2020，37（4）：871-880.

［17］ JIANG Z，JAMES D J M，Ren J J，et al. Proxy-based sliding-mode tracking control of dielectric elastomer actuators through eliminating rate-dependent viscoelasticity［J］. Smart Materials and Structures，2022，31（7）：518-528.

［18］ LI Y L，INKYU O，CHEN J H. Nonlinear dynamic analysis and active control of visco-hyperelasticdielectric elastomer membrane［J］. International Journal of Solids and Structures，2018（152/153）：28-38.

［19］ 樊亞玲，杨宏亮. 双轴预拉伸下介电弹性体驱动器力电稳定性分析［J］. 金属功能材料，2016，23（2）：40-44.

［20］ CHEN H L，ZHANG J S，LI B，et al. Tunable active vibration attenuation using highly deformable dielectric elastomers［J］. Smart Materials and Structures，2015，24（11）：115033.

Abstract：This paper proposes an adaptive Radial Basis Function （RBF） neural network sliding mode control （SMC） algorithm for the trajectory tracking control of dielectric high-elasticity polymers. Firstly，the unknown terms in the kinetic model caused by hyperelasticity and viscosity，and the uncertainty of the model caused by external disturbance are considered. The controller is designed by using the arbitrary approximation of continuous function property of RBF neural network，the robustness of sliding mode control，and the online adjustment of control rate by adaptive control. The Lyapunov function is then constructed to demonstrate the stability of the controller as a means of achieving tracking control of the dielectric polymer trajectory. The results show that the extreme value error of the polymer position tracking is less than 1% and the response time is 0.7 s，indicating that the system has high dynamic performance and achieves linear motion trajectory tracking of the structure. Finally，the influence of excitation frequency and width pre-stretch ratio on the tracking trajectory of the structure is analysed，and an optimisation method of the coefficient parameters is designed. The results show that the effectiveness of the optimisation method improves the accuracy of the trajectory tracking，and also verifies that the proposed control system has strong self-adaptability and stability，which provides a theoretical basis for the research of bionic drive and trajectory tracking control of soft robots.

Key words：dielectric high-elastic polymer； hyperelasticity； viscoelasticity； radial basis function neural network； sliding mode control