支持全整数推断的神经网络递增定点量化算法研究

杨会渠 杨国为 何金钟 徐健

摘要：为了解决量化模型不支持全整数推断及共享指数受奇异值影响等问题，本文提出一种支持全整数推断的神经网络递增定点量化算法（integer-only incremental quantization，IOIQ）。通过将神经网络权重和特征从浮点数据转换为带有整数共享指数（integer-shared exponent，INT-SE）的数据，实现浮点模型的有效压缩。在伪量化训练中，IOIQ算法采用递增量化策略，对浮点数据进行逐步量化和迭代更新，弥补了一次性量化精度损失较大的不足。为解决推理时数据溢出问题，通过分别统计神经网络模型每层量化数据共享指数的差异，确定各层输出特征的最佳截位点，并给出了量化模型在推理侧的硬件实现方案，而经IOIQ算法量化的神经网络模型，在推断过程中不含任何浮点数据，全部为整数运算，易于边缘侧部署。实验结果表明，在8 bit位精度下，经IOIQ算法量化后的ResNet50，在CIFAR数据集上，top-1准确率下降0.2%，在ImageNet数据集上，top-1准确率下降0.58%，性能优于高效纯整数推理和递增网络等量化方法。该研究具有重要的实际应用价值。

关键词：神经网络； 量化； 全整数； 共享指数； 递增量化； 最佳截位点

中图分类号：TP183 文献标识码：A

文章编号：1006-9798（2023）02-0010-08； DOI：10.13306/j.1006-9798.2023.02.002

基金项目：国家自然科学基金面上项目（62172229）

作者简介：杨会渠（1998-），男，硕士研究生，主要研究方向为AI加速芯片和神经网络模型压缩。

通信作者：杨国为（1964-），男，博士，教授，硕士生导师，主要研究方向为智能信息处理、模式识别和智能控制。Email：ygw_ustb@163.com

神经网络模型压缩技术致力于在不显著降低模型性能的情况下，减少计算资源和存储空间的消耗［1-3］，主要包括剪枝［4］、量化［5-10］、知识蒸馏［11］、紧凑神经网络设计［12-15］等方法。模型量化因其能够简易部署和加速硬件推理，引起了世界各国学术界和产业界的广泛关注。LIN D等人［16］提出了一种共享指数的定点数据，通过监控权重中的最大值来确定共享指数；B.JACOB等人［17］提出了高效纯整数推理的量化算法（integer-arithmetic-only，IAO），并采用了伪量化训练的思想，在硬件设备上得到了较好的验证；ZHOU A等人［18］提出递增量化算法（incremental network quantization，INQ），该算法一次量化一部分数据，让未量化的数据微调后再进行量化，直至数据全部量化完毕。虽然上述部分研究工作完成了全定点数据的设计，但它们直接通过最大值和最小值选取共享指数，导致共享指数受到奇异值影响，使定点数据偏移浮点数据。一些研究者为了保证模型的性能，没有完全量化模型（只量化了权重），加大了硬件部署的困难。综合上述分析，为了解决量化模型不支持全整数推断、共享指数受奇异值影响等问题，本文提出了支持全整数推断的神经网络递增定点量化算法。该算法以带有共享指数的整型数据表示浮点数据，通过统计浮点数据分布，确定最佳共享指数，保持了数据的有效精度，并通过递增量化对定点数据微调，最终得到神经网络量化模型。该量化模型支持全整数推断，能够加快模型推理速度，降低了轻量化设备部署的难度。该研究解决了奇异值影响共享指数的问题，具有一定的创新性。

1 IOIQ算法

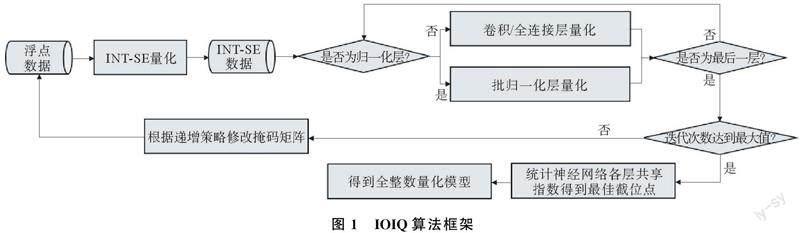
IOIQ算法是一种为全整数推断而设计的量化算法，支持将权重和激活都量化为8 bit，甚至更低的比特。IOIQ的算法框架如图1所示，输入浮点训练样本，待量化训练完成后，输出量化模型。

IOIQ算法包括INT-SE数据量化和递增量化2部分。其中，INT-SE數据量化策略贯穿整个量化过程，递增量化则是通过每个迭代周期更新掩码矩阵，实现对权重数据的逐步量化。IOIQ算法接收到一组浮点数据后，首先通过INT-SE量化方法将浮点数据量化为INT-SE数据，并根据不同的神经网络层（卷积层/全连接层或批归一化层），将INT-SE数据送入不同的量化模块。其中，在卷积层/全连接层量化模块中，先将浮点权重数据量化为INT-SE数据，再将其与原始浮点权重数据组合成复合权重进行计算，最后将该层的输出特征量化为INT-SE数据。在批归一化层量化模块中，先迭代学习方差和均值，然后锁定参数，简化计算方式，待所有神经网络层均计算完毕后，根据递增量化策略，更新掩码矩阵。重复上述过程，直到达到最大迭代次数，训练完毕。最后统计各层的共享指数差异，计算输出特征最佳截位点，最终得到神经网络量化模型。

1.1 INT-SE数据量化策略

为了最大程度减少存储消耗，本文提出一种专用于整数计算的INT-SE数据格式。INT-SE数据之间所有的计算全是整型数据之间的乘加运算，计算更加简单，方便硬件设计。

INT-SE数据包含表示数据部分的数据D（Data）和表示数据部分所有成员小数点位置的共享指数s（shared exponent）2部分。INT-SE数据可表示的浮点数值T为

在INT-SE数据中，共享指数s是一个能够表示数量级，并且影响量化数值范围的值，其扮演的角色相当于量化系数。因此，为了减少参数量，使计算更加简便，在IOIQ算法中，每一个层的参数仅设置一个共享指数。为了更加精确地表示量化数值，减少误差，IOIQ算法以均方误差（mean square error，MSE）为指标，选取最佳共享指数。MSE代表了量化前后参数向量的欧氏距离，MSE越小，表示量化前后的值越接近。INT-SE数据量化流程如图2所示。

在上述过程中，随着迭代采用不同的掩码矩阵，使权重矩阵实现了递增式的量化。IOIQ算法采用两种策略，以获得掩码矩阵，即随机策略和剪枝策略。其中，随机策略将会根据量化比例，随机生成掩码矩阵；剪枝策略根据当前层神经网络中权重的绝对值大小和量化比例，设置掩码矩阵。

1.3 批归一化层及偏置量化方法

卷积层和全连接层可以直接将权重转化为INT-SE数据，但批归一化层有4种不同的参数，且推理侧中的均值和方差是训练过程中的均值和方差，是通过滑动平均得到。此时，批归一化层含有除法和开方等复杂运算，为了能够简化批归一化层的计算方式，让批归一化层更加适应硬件设计，并且避免量化批归一化层模型精度的损失。IOIQ算法针对批归一化层量化训练，提出了学习参数和锁定参数两种不同批归一化层的计算方式。

首先通过学习参数计算方式更新滑动均值μ和滑动方差σ2，并通过锁定参数将4种参数融合后量化，进而通过式（8）计算出浮点输出特征，最后将浮点输出特征量化为INT-SE数据的输出特征送往下一层计算。由于偏置需要与乘法或卷积的临时结果进行累加，如果偏置的共享指数小于临时结果的共享指数，就会增加计算困难。因此，在IOIQ算法中，先对偏置进行统计，计算出参考共享指数，然后对其进行限定，如果加法对象的共享指数为s，那么偏置的共享指数取值范围确定在［s+7，s］范围内。在确定偏置共享指数后，将偏置从浮点数据量化为INT-SE数据。批归一化层锁定参数量化训练流程如图5所示。

1.4 量化模型在推理侧的硬件实现方案

神经网络量化模型在推理侧硬件实现时，仅乘加运算导致数据溢出时会造成精度的损失，其他的乘加运算和移位操作都不会损失精度。因此，为了避免数据溢出，保留数据精度，IOIQ算法在完成量化训练后，统计神经网络每一层的权重共享指数sw、训练过程中输入共享指数的滑动平均值sin和输出共享指数的滑动平均值sout，计算最佳截位点（optimal truncation point，OTP），最佳截位點POT为

在硬件中，量化后，卷积层、全连接层和批归一化层全整数计算流程如图6所示。图6中，输入的整型数据Din和权重的整型数据Dw，会不断进行整数乘加运算，得到临时结果的整型数据Dt1，临时结果的共享指数st1是输入共享指数sin与权重共享指数sw的和。为了与临时结果数据对齐，偏置的整型数据Db要根据st1和sb进行移位操作后与临时结果Dt1累加，得到累加结果Dt2。经过多次累加操作，累加结果的数据位宽最大可扩展到32位，为了输出数据和输入数据保持同样的数据位宽，将Dt2、st2和最佳截位点POT，通过舍入与截断操作（R&T），得到与输入数据同样数据位宽的输出数据Dout和sout。

2 实验与结果分析

2.1 实验设计

为充分验证IOIQ算法的性能，本文设计多比特实验、共享指数实验和递增量化实验，并与典型的神经网络量化算法BWN［19-20］、TWN［21］、INQ［18］、FGQ［22］、IAO［17］进行了对比分析。实验中，考察了ResNet18［23］、ResNet34［23］、ResNet50［23］和轻量级网络MobileNetv2［14］4种神经网络模型的量化结果。

数据集采用CIFAR和ImageNet。其中，CIFAR数据集［24］包含8 000万张微型带标签图像；ImageNet数据集［25］包含约120万张训练图像和5万张验证图像。

2.2 实验结果与分析

2.2.1 多比特实验结果

神经网络模型由浮点数据量化为不同位数INTS-SE数据，IOIQ算法不同比特量化实验结果如表1所示。

由表1可以看出，ResNet18在CIFAR10下，16 bit量化后准确率较FP32上升了0.02%，12 bit上升了0.01%，8 bit下降了0.03%，6 bit下降幅度最高，达到了4.35%。实验结果表明，在高比特出现了超越浮点准确率的现象。因为目前的深度神经网络普遍存在冗余，将网络适当量化可能会减少冗余，从而提升模型泛化能力，而过低的比特位由于信息量太少，会导致精度下降，如6 bit量化。本实验与原浮点模型相比，8 bit量化结果仅下降了0.03%。因此，本文IOIQ算法在8 bit位上取得最优的性能平衡，后续实验基于8位量化展开。

2.2.2 共享指数实验结果

给出不同共享指数候选集对量化模型性能的影响结果，不同的共享指数候选集实验结果如表2所示。表2中，s代表初始共享指数，+1代表统计得到的共享指数+1。

由表2可以看出，当s-1，s，s+1，s+2，s-2这5个共享指数候选值单独作为候选集进行量化实验时，量化模型效果最好的是初始共享指数s，ResNet18准确率仅下降了0.43%；最差的是s-2，准确率下降了22.2%。2个共享指数候选值比1个共享指数候选值得到的量化模型性能更好，仅仅下降了0.3%左右；4个共享指数候选值得到的量化模型性能最优，ResNet18量化后准确率仅下降0.18%。实验结果表明，单一的共享指数不能使INT-SE数据表达精确，更多的共享指数作为候选值，能够克服奇异值对共享指数的影响，让INT-SE数据表达更加精确。综合考虑性能与时间成本，最后选择4个候选值作为候选集选取最优共享指数。

2.2.3 递增量化实验结果

给出剪枝递增和随机递增2种递增量化策略对模型性能的影响，不同递增量化方法对比结果如表3所示。由表3可以看出，在CIFAR10数据集上，ResNet18使用剪枝递增策略得到的量化模型，准确率仅下降0.18%，使用随机递增策得到的量化模型，准确率下降0.37%。

表3证明了使用剪枝递增策略得到的量化模型，性能更加优秀，因为神经网络对于权重参数比较敏感，绝对值大的权重对结果的影响比较大，若进行随机量化，绝对值大的权重可能在最后一次进行量化，需要更长的训练周期进行微调，因此IOIQ算法使用剪枝递增策略对权重进行量化。

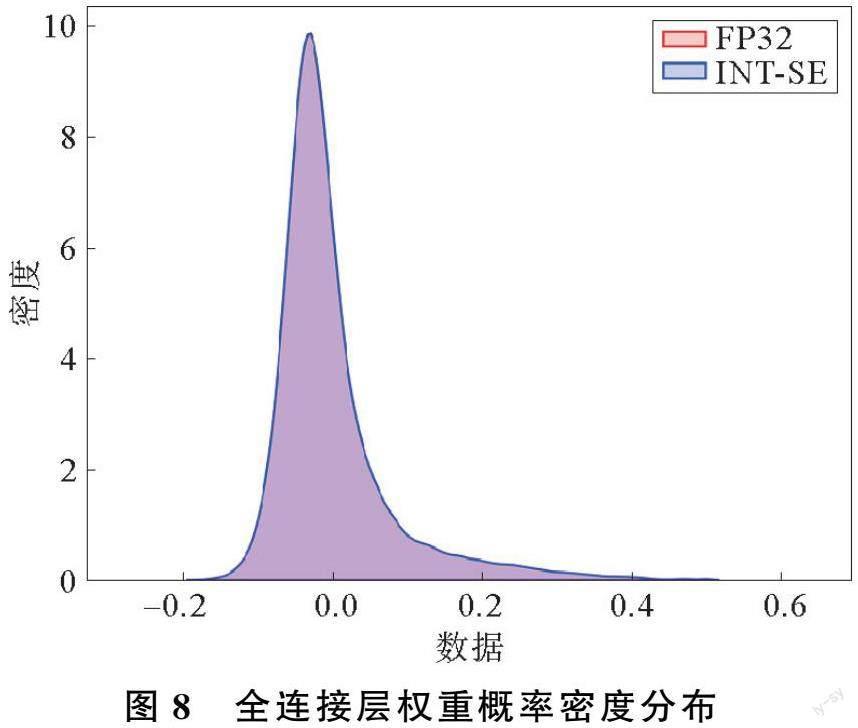
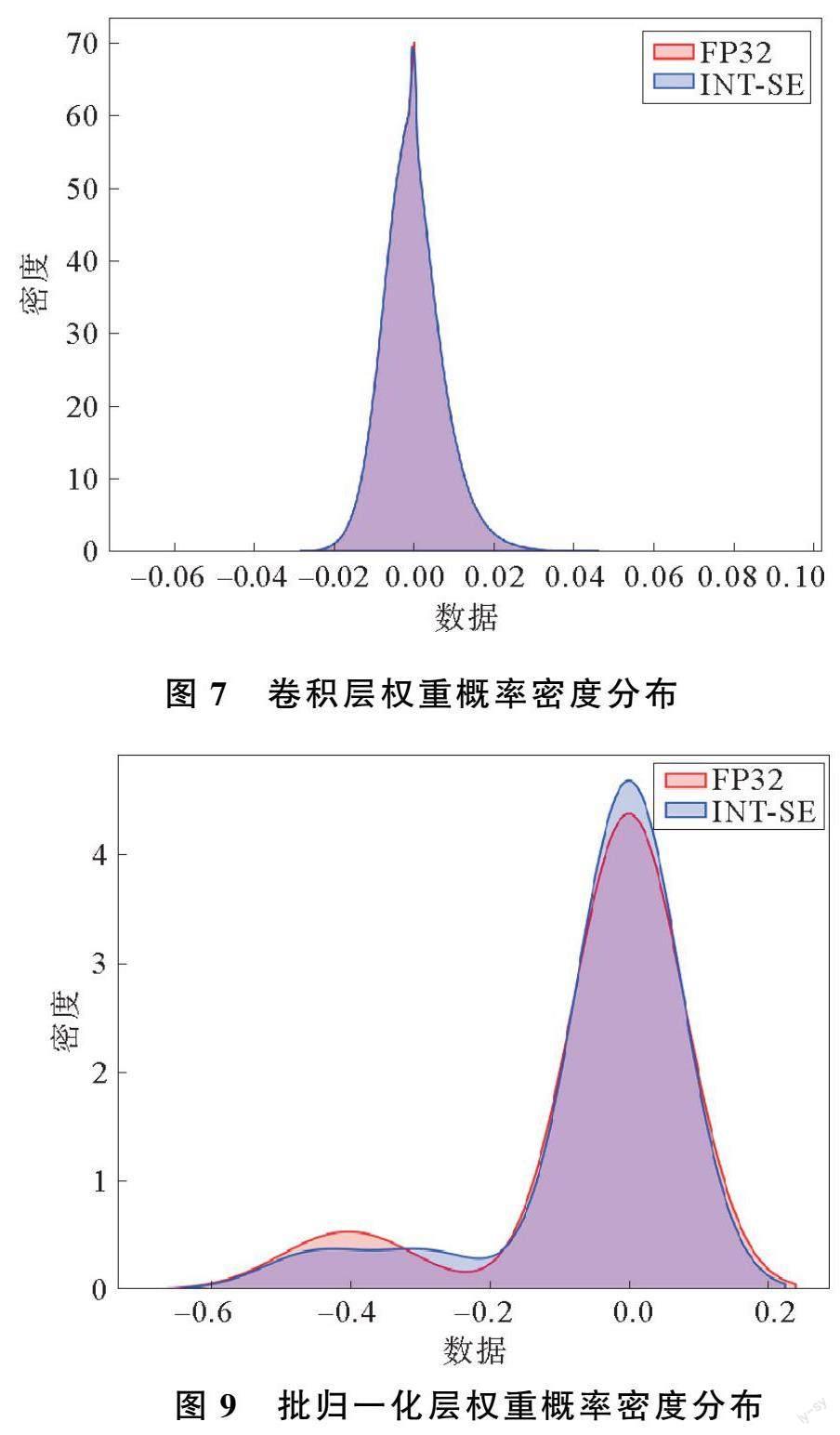
为了查看量化前后数据是否一致，分别显示ResNet18在CIFAR10数据集的浮点模型和量化模型权重参数概率密度分布。量化前后，卷积层权重概率密度分布如图7所示，全连接层权重概率密度分布如图8所示，批归一化层权重概率密度分布如图9所示。

由图7～图9可以看出，卷积层和全连接层浮点模型和量化模型权重分布基本一致，只在批归一化层会有一些量化损失。因为批归一化层4个参数量化后直接锁定，没有经过训练进行微调，使一些数据偏移了浮点数据。

2.2.4 与其他算法比较结果

在与其他算法进行对比之前，首先对IOIQ算法进行扩展实验，不同网络基于IOIQ算法的实验结果如表4所示。由表4可以看出，在CIFAR10数据集上，ResNet50量化后，准确率下降0.2%；在CIFAR100数据集上，ResNet50下降0.52%；在ImageNet数据集上，ResNet50下降了0.58%，MobileNetv2下降了0.35%。

为了进一步证明IOIQ算法的性能，将IOIQ算法与BWN［19-20］、TWN［21］、INQ［18］、FGQ［22］、IAO［17］进行对比试验，Resnet50在ImageNet上的不同方法性能对比结果如表5所示。由表5可知，IOIQ算法的性能优于其他算法，与IAO算法相比，其准确率高0.92%，并且本文的算法改进了其他算法不支持全整数推断、共享指数受奇异值影响和一次量化精度下降的缺点，更加适应硬件设计。

3 结束语

本文提出了支持全整数推断的神经网络递增定点量化算法IOIQ，通过INT-SE量化方法，将神经网络的参数量化到整型数据，并通过递增量化微调数据。其中，通过将MSE作为指标，选取最优的共享指数，解决了奇异值影响共享指数的问题。针对一次性量化带来量化精度下降问题，IOIQ使用改进的递增量化算法，每次仅量化一部分数据，且量化后的数据仍然可更新。由于对整数运算存在数据溢出的问题，在训练结束时，统计了神经网络各层的共享指数，得到输出特征的最佳截位点，在量化完成后，量化模型中参数全部为INT-SE数据，极大地节省了存储空间，且模型推断计算过程全部是整数的乘加运算，加快了运算速度，更加适应硬件设计。实验结果表明，IOIQ算法在ResNet和MobileNet网络上取得了较好成果，经IOIQ算法量化后的ResNet50，在CIFAR数据集上的top1，准确率下降0.2%，在ImageNet数据集上top1，准确率下降0.58%，证明了本研究方法的有效性。为了探索硬件加速的极限，未来可进一步研究更低比特位量化的策略。

参考文献：

［1］ NAN K，LIU S，DU J，et al. Deep model compression for mobile platforms：A survey［J］. Tsinghua Science and Technology，2019，24（6）：677-693.

［2］ HU D，KRISHNAMACHARI B. Fast and accurate streaming CNN inference via communication compression on the edge［C］∥2020 IEEE/ACM Fifth International Conference on Internet-of-Things Design and Implementation （IoTDI）. Sydney，NSW，Australia：ACM，2020.

［3］ YEJING L A I，SHANFENG H A O，DINGJIANG H. Methods and progress in deep neural network model compression［J］. Journal of East China Normal University （Natural Science），2020（5）：68-82.

［4］ ALVAREZ J M，SALZMANN M. Learning the number of neurons in deep networks［C］∥ In Proceedings of the 30th International Conference on Neural Information Processing Systems （NIPS′16）. Red Hook，NY，USA：Curran Associates Inc，2016：2270-2278.

［5］ 丁文銳，刘春蕾，李越，等. 二值卷积神经网络综述［J］. 航空学报，2021，42（6）：192-206.

［6］ RASTEGARI M，ORDONEZ V，REDMON J，et al. Xnor-net：Imagenet classification using binary convolutional neural networks［C］∥European Conference on Computer Vision. Amsterdam，Netherlands：Springer，Cham，2016：525-542.

［7］ CHEN W，WILSON J T，TYREE S，et al. Compressing neural networks with the hashing trick［C］∥International Conference on International Conference on Machine Learning. Lille，France：JMLR，2015：2285-2294.

［8］ HAN S，MAO H，DALLY W J. Deep compression：Compressing deep neural networks with pruning，trained quantization and huffman coding［J/OL］. arXiv preprint arXiv：1510.00149，2015.

［9］ COURBARIAUX M，BENGIO Y，DAVID J P. BinaryConnect：Training deep neural networks with binary weights during propagations［C］∥International Conference on Neural Information Processing Systems. Montreal，Canada：MIT Press，2015：3123–3131.

［10］ QIN H，GONG R，LIU X，et al. Forward and backward information retention for accurate binary neural networks［C］∥2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition （CVPR）. Seattle，WA，USA：IEEE，2020：2247-2256.

［11］ HINTON G，VINYALS O，DEAN J. Distilling the Knowledge in a Neural Network［J］. Computer Science，2015，14（7）：38-39.

［12］ IANDOLA F N，HAN S，MOSKEWICZ M W，et al. SqueezeNet：AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size［J/OL］. arXiv preprint arXiv：1602. 07360，2016.

［13］ HOWARD A G，ZHU M，CHEN B，et al. Mobilenets：Efficient convolutional neural networks for mobile vision applications［J/OL］. arXiv preprint arXiv：1704. 04861，2017.

［14］ SANDLER M，HOWARD A，ZHU M，et al. MobileNetV2：Inverted residuals and linear bottlenecks［C］∥ 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition （CVPR）. Salt Lake City，UT，USA：IEEE，2018：4510-4520.

［15］ HOWARD A，SANDLER M，CHEN B，et al. Searching for MobileNetV3［C］∥2019 IEEE/CVF International Conference on Computer Vision （ICCV）. Seoul，Korea（South）：IEEE，2020：1314-1324.

［16］ LIN D，TALATHI S，ANNAPUREDDY S. Fixed point quantization of deep convolutional networks［C］∥International conference on machine learning. New York，USA：PMLR，2016：2849-2858.

［17］ JACOB B，KLIGYS S，CHEN B，et al. Quantization and training of neural networks for efficient integer-arithmetic-only inference［C］∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City，UT，USA：IEEE，2018：2704-2713.

［18］ ZHOU A，YAO A，GUO Y，et al. Incremental network quantization：Towards lossless cnns with low-precision weights［J/OL］. arXiv preprint arXiv：1702. 03044，2017.

［19］ HUBARA I，COURBARIAUX M，SOUDRY D，et al. Quantized neural networks：Training neural networks with low precision weights and activations［J］. The Journal of Machine Learning Research，2017，18（1）：6869-6898.

［20］ LENG C，DOU Z，LI H，et al. Extremely low bit neural network：Squeeze the last bit out with admm［C］∥Thirty-Second AAAI Conference on Artificial Intelligence. Louisiana，USA：AAAI，2018：3466-3473.

［21］ LI F，ZHANG B，LIU B. Ternary weight networks［J/OL］. arXiv preprint arXiv：1605. 04711，2016.

［22］ MELLEMPUDI N，KUNDU A，MUDIGERE D，et al. Ternary neural networks with fine-grained quantization［J/OL］. arXiv preprint arXiv：1705. 01462，2017.

［23］ HE K，ZHANG X，REN S，et al. Deep residual learning for image recognition［C］∥2016 IEEE Conference on Computer Vision and Pattern Recognition （CVPR）. Las Vegas，NV，USA：IEEE，2016：770-778.

［24］ ALEX K，HINTON G. Learning multiple layers of features from tiny images［R］. Toronto：University of Toronto，2009.

［25］ JIA D，WEI D，SOCHER R，et al. ImageNet：A large-scale hierarchical image database［C］∥ 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami，FL，USA：IEEE，2009：248-255.

Abstract：To port convolutional neural networks to lightweight devices，this paper proposes incremental fixed-point quantization algorithm for neural networks supporting integer-only inference （IOIQ）. The effective compression of the floating-point model is achieved by converting the neural network weights and features from floating-point data to data with integer-shared exponent （INT-SE）. In the pseudo-quantization training，the IOIQ algorithm adopts incremental quantization strategy to gradually quantize and iteratively update the floating-point data，which makes up for the large loss of one-time quantization accuracy. To solve the data overflow problem during inference，the optimal cutoff point of the output features of each layer is determined by separately counting the difference of the quantized data sharing index of each layer of the neural network model，and the hardware implementation scheme of the quantized model on the inference side is given，while the neural network model quantized by the IOIQ algorithm does not contain any floating-point data during inference，and all of them are integer operations，which are easy to deploy on the edge side. Experimental results show that the top-1 accuracy of ResNet50 quantized by the IOIQ algorithm decreases by 0.2% on the CIFAR dataset and by 0.58% on the ImageNet dataset at eight-bit precision，outperforming the algorithm of efficient integer-arithmetic-only inference （IAO） quantization and incremental network quantization （INQ）. This research has important practical applications.

Key words：neural network； quantization； full integer； shared exponential； incremental quantization； optimal cutoff point