导线测量超限情境下错误边角确定的设计与实现

胡家豪　张爱国　苏世星

摘 要：在进行导线测量时，受仪器、外界环境等观测条件影响测量中经常会出现各种各样的错误，而这些错误有可能会导致导线角度闭合差或者全长相对闭合差超限。为了准确找出造成成果超限的观测数据，需要耗费大量的人力、物力进行计算和分析。为此，本文设计和实现了一个在确定导线超限以后，能够快速找出错误转折角或边长等观测数据的应用程序。最后，在IntelliJ IDEA+PostgresSQL数据库的编程环境下，实现了导线测量超限情境下错误边角的快速确定，提升了测绘信息化发展水平。

关键词：导线测量；错误边角；IntelliJ IDEA；JAVA；数据库

中图分类号：P214  文献标识码：A  文章编号：1673-260X（2023）03-0037-06

1 引言

在當前测绘和信息技术的不断发展下，对于导线测量的精度和便捷性要求也变得越来越高。不同国家的研究人员积极地开展了这方面的研究，伊朗的H.Amini.S. Mehrdad对比了三种不同的调整误差的方法，并进行了优化增加了在导线测量方面的精确度[16]。赵普分以矿井中的实际工作情况为例，通过陀螺仪定向解决了测量精度不达标的问题，减少了一些因为工作环境的问题而引起的误差[1]。熊鹏飞等人研究了矿井内控制测量改善布设方案，采用了无定向支导线测量网布设的新方法[2]。除了研究通过改变布设来增加导线测量的精度之外，还有很多人致力于研究关于如何查找错误边角这一问题。

一般导线的测量错误都是出现在观测角度和平距上，如果观测角出错就会导致闭合角超限，平距出错就会导致全长闭合差超限，但凡其中一个出现问题都需要通过计算来找出错误点，并对错误点重新进行测量，不过在查找错误以前我们仍然需要进行一些工作来确保其他步骤没有出错。首先是我们测量出来的数据有没有抄写错误，还有就是计算时是否有出现公式错误或者用错数据的现象[3]。

随着科技的发展，许多软件也在导线测量中发挥着重要的作用，例如Excel宏运算、Matlab计算、VB开发和AutoCAD绘图等[4，5]。AutoCAD是一个十分常见的平面绘图软件，这个软件不仅操作简单，而且绘制出来的几何图形也十分精准，它不仅可以将我们测量得到的导线精准绘制出来，还可以自动获得坐标和坐标增量等数据，无需计算，大大加快了整体进度[6]。

但是无论用什么工具或软件来帮助计算，始终可能会出现一些不可避免的错误发生，这会导致浪费大量的人力物力和时间，尤其是对一些刚刚接触相关工作不太熟悉的新人来说，因此一个能直接帮助我们判断出是边错误还是角错误，并快速找出错误点的程序就变得很有必要了。

设计与实现的总体框架如下图1所示。

架构图分为以下三个模块：访问层，逻辑层和应用层。

访问层使用的是PostegreSQL 14来对数据进行存储和管理。逻辑层将使用IntelliJ IDEA Community Edition进行代码的编写，程序的主要功能为错误边角的查询。最后应用层为该程序可使用的领域，在进行水利工程，建筑道路过程和地下工程等项目时，都需要用到导线测量。

2 导线测量超限情境下错误边角确定方法

2.1 数据采集与获取

本文的研究内容为设计出一个在确定了导线超限的情况下帮助我们找出错误边角的程序。因此需要收集一些数据来帮助我们测试程序的结果是否正确，为了保证程序的正确率，不能单单只用一组数据来进行验证，要保证数据的多样性，并且要将闭合导线与附和导线全部都考虑进去，并且人为地制造一些错误点。在选取数据的时候要选取完整的导线测量数据，其中包括各观测点名字，观测角度数，观测点的起始坐标方位角和终点坐标方位角，该观测点与相邻观测点的平距，起始坐标和中点坐标等关键数据，并且在使用这些数据之前需要提前进行人工计算，保证这些数据的全长闭合差和角度闭合差在限差以内。

本文所选取的数据库为PostgreSQL数据库，PostgreSQL数据库在GIS领域有着其独特的优势，虽然结构上比较复杂，但是它的功能也是相当丰富的，它还有着稳定性高、速度快、具有开源性等优势，因此也得到了越来越多用户的信赖，用户也变得越来越多了[7，8]。

为了保证测试数据的质量和数据的可靠性，我将从课本《数字地形测量学》中选取的数据进行测试。我最终选用的数据是书本P180上的附和导线表5-4，主要数据内容如下表1所示。

在拿到导线测量数据之后首先需要计算出测量数据的角度闭合差和全长相对闭合差，以确保数据是在限差以内，方便后续的程序检验，之后在程序设计完毕之后，根据检验需要再将其录入数据库。

2.2 错误角确定方法

在确定导线测量错误测角方面，经过多年的发展，已经有了相当成熟的查找确定方式[9]，如下图 2所示，如果符合导线出现错误，我们可以利用没有经过平差计算改化的观测角从B到C计算导线边各个位置的坐标方位角以及坐标，并用同样的方法从C倒推到B，通过对比这两组坐标我们会发现，有一点的两个观测点的坐标非常相似，而其它观测点坐标会有比较大的差异，由此我们就能确定坐标相似的这个点就是错误角发生的导线点。同样的对于闭合导线，也是采用相同的方法来查找错误角的位置，从一点开始以顺时针和逆时针两个方向按同样的方法分别推算各个位置的坐标方位角和坐标。

考虑到程序实现的可行性，所以本次错误边角查找方式选取为上述方式，具体梳理计算流程及公式如下：

首先计算出角度闭合差，并于限差进行比较，确定角度闭合差是否超限，角度闭合差计算如公式1所示[9]。

其中f？茁为角度闭合差值，∑Z测为测量到的附和导线观测角内角和，∑Z理为理论上附和导线观测角内角之和，n为导线边数，？琢AB是坐标方位角的起始方位角，？琢CD是坐标方位角的终点坐标，当观测角内角为左角时，？琢AB为正，？琢CD为负，当观测角内角为右角时，？琢AB为负，？琢CD为正。

计算完成后如果角度闭合差超限，则需要顺时针和逆时针推算每条导线边的坐标方位角和每个导线点的坐标，使用到公式2[10]。

其中，？琢前为导线下一个观测点的坐标方位角，？琢后是导线当前位置观测点的坐标方位角，？茁为导线观测点的观测角度数，公式中“±”取决于观测角的方向是左角还是右角，当观测角为左角时取”+”，反之为”-”，为了确保坐标方位角？琢前的取值范围在0～360°之间，当？琢前大于360°时要减去360°，小于0时要加上360°。

当我们计算完所有的坐标方位角的数值之后，就可以用坐標方位角和平距计算对应位置的坐标增量和坐标了，具体推算公式如下所示。

其中，x后和y后是我们当前位置的坐标，x前、y前是下一个观测点的坐标，？驻x、？驻y为坐标增量，S为相邻两个观测点的距离。完成从起点开始推算导线坐标后，我们就要从导线的终点坐标开始重新倒推一遍，将最后得到的两组坐标进行对比，坐标最为接近的一组就是我们要找的错误角的位置[11]。

2.3 错误边确定方法

在确定角度闭合差没有超限后，我们就要去判断是否是全长闭合差超限了。全长闭合差如果超限了，一般是以下两种原因导致的：

（1）我们所测量出来的平距有问题。

（2）计算时没有用对应的坐标方位角进行计算。

如果是平距出现问题，这会导致我们计算出来的全长闭合差的坐标方位角与其中一个坐标方位角近乎相等如图2所示，那么用来与这个坐标方位角相乘计算坐标增量的平距就是我们要找的错误边。如果使用不对应的坐标方位角计算了坐标增量，那么我们计算出来的全长闭合差的坐标方位角会与其中一个坐标方位角的差值为90°左右。因为我们是用程序来进行计算坐标与坐标增量等数据的，所以不用考虑出现第二种情况的可能性。

下面我们来介绍一下怎么去计算全长闭合差的坐标方位角。首先我们用计算得到所有的坐标方位角，然后用对应的平距与cos的坐标方位角相乘就可以得到坐标增量？驻x，用对应的平距与sin的坐标方位角相乘就能得到坐标增量？驻y[12]。将所有的坐标增量相加得到坐标增量和fx与fy。之后用起点坐标与终点坐标相减就能得到差值x与差值y。将得到的这两组数据相减然后正切就能得到象限角a，再根据象限角a所在的象限进行转换就能得到全长闭合差的坐标方位角了。具体公式如下所示。

最后我们将得到的坐标方位角a与之前求得的坐标方位角进行对比，就能找出错误边是哪个了。

3 错误边角确定的系统设计

3.1 系统功能及整体框架

我们是用全站仪测得的数据是无法直接使用的，当我们完成外业观测，想使用全站仪数据的时候可以将全站仪内的数据导出为文本格式（.txt）的文件来使用。获得全站仪的数据后，我们就可以将数据存储到数据库中，并使用这些数据进行错误边角的计算。数据处理流程如下图4所示。

3.2 数据存储设计

在录入数据之前，我们要先在PostgreSQL里面将表格给建好。表名为clsj，表属性和字段的设计如下表所示。表中的cz表示测站的名字，gd、g、gm分别为观测角度数的度、分、秒，fd、ff、fm分别代表坐标方位角的度、分、秒，s表示平距，x和y表示的是坐标，id设置为key是为了让我们在对数据进行过修改之后不会把顺序给打乱[13，14]。

用数据库存储数据时我们还要使用数据库代码来插入或修改数据，为了方便使用我还设计了一个用于读入数据的程序和一个简易的界面，图形界面如下图5所示。有了这个程序之后我们就可以很方便地进行数据的存储了，不过在此之前我们依旧需要先在数据库中把表格创建好。我们先将我们测得的数据按我们事先设定好的格式写入一个文本文件内，之后我们将我们的文本文件存放的地址填入图中的文件存放路径中，程序就会将该文件路径下的所有txt文本格式的文件都读入到数据库中。再输入我们所存储的数据库的用户名和密码，以此来实现不同数据库的连接来对不同的项目进行区分，最后将对应的表名输入到相应的位置，可以根据不同的项目或需求修改，以方便分类、管理不同项目的数据信息。完成了上述的步骤之后就可以将我们的数据存入相应的数据表中了，有了这个程序后我们就可以减少数据库的使用，只要通过文本文件就可以进行存储，使用起来会更加方便。

3.3 错误角确定设计

具体程序功能流程图如图6所示。

到此我们的错误角推算过程已经结束了，但是有时候直接将两组坐标拿出来对比可能不够直观，这时我们可以通过增加一条关于坐标距离的计算公式来帮助我们更快地找出错误角的位置。这样我们只要找出距离最小的点就能判断出错误角的位置了，具体公式如公式12所示。

其中，d为两坐标之间的距离，x和y为当前位置的正算坐标，x逆和y逆为当前位置的反算坐标。

3.4 错误边确定设计

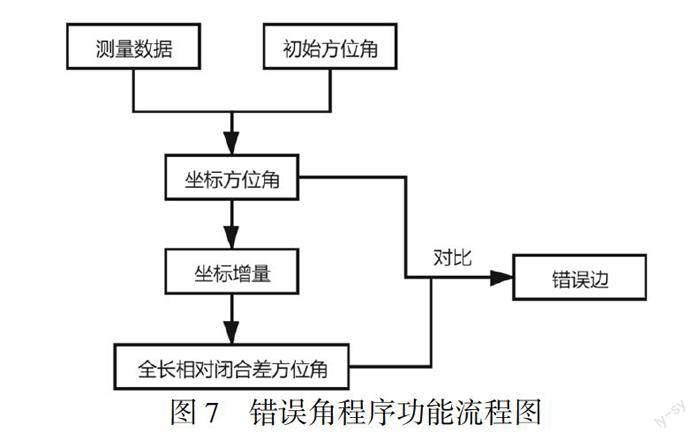
具体流程如下图7所示。

4 错误边角确定的系统实现

4.1 系统软件实现

本论文的主要目的就是通过将上述公式代码化，用电脑代替人来进行计算，以此来避免人为因素造成的计算错误，并大大提高了工作效率，减少了人力上的浪费。为了检测测序计算出来的结果是否准确我将以一条符合导线的测量数据为例来进行检测，其主要测试过程为：

（1）将测试数据上传到本地数据库当中，并将数据从数据库里提取出来。

（2）先对测试数据进行计算判断导线是否超限，如果测试数据的角度闭合差超限，我们就进入错误角计算模块进行计算，我们先用导线起始位置的坐标方位角和坐标来正推出终点位置的坐标，然后再用导线终点位置的坐标方位角和坐标来倒推出起始点位置的坐标，将得出的两组数据相同观测点的坐标距离进行计算，最后输出这些结果；如果角度闭合差未超限，那么就可以确定是边错误，前一部分的计算流程与角错误一致，先算出各个观测点的坐标方位角和坐标增量，之后算出全长闭合差的坐标方位角a，最后输出计算结果与之前得出的坐标方位角进行对比。

（3）显示计算结果。

具体流程如图8所示：

为了方便测试数据的存储和修改，这些导线的测试数据会被保存到PostgreSQL数据库中，这样就能方便我们在需要的时候能随时将这些数据提取出来使用，并提取到IDEA中进行计算。

在使用IDEA帮助我们计算前，我们要先使用数据库函数获取本地数据库的IP地址，再输入端口号，用户名，密码和数据库名来实现IDEA和PostgreSQL数据库的连接，再按顺序将表格里的内容导入进来，分别将观测角度数，起始与终点坐标方位角，平距，起始坐标和终点坐标的数据存入长度为n不同的数组变量中，n为导线观测点个数，在导入完数据之后我们就可以开始计算了。

程序的运行流程如图9所示，前端会把我们获得的数据记录到数据库中，我们再将数据库中的数据读取到程序里，最后程序会对数据进行计算并返回计算结果输出错误边角所在的位置。

4.2 系统应用与运行效果

运行程序的设备如下所示：

运行设备：联想Y7000P

操作系统：Window10家庭中文版

处理器：Intel（R） Core（TM） i7-9750H CPU @ 2.60GHz 2.59 GHz

系统类型：64位操作系统，基于x64的处理器

系统开发测试环境：PostgreSQL、IntelliJ IDEA Community Edition

通过人工计算来校验程序计算结果的时候我们就能发现边角错误的计算确实是一件相当复杂且繁琐的工作，而且容易发生计算错误。但是对于计算机来说这个计算量可是太小了，只需短短1秒钟就能完成计算并给出计算结果，大大节省了人力物力。而且计算机给出的结果更加清晰，能帮助我们快速地判别出错误点的位置。下面我将通过人为的方式来制造错误点，结果如下所示：

（1）错误角查找结果。我将P3点的观测角度数从123°改为30°，我们可以从程序运行的结果中看到，两组坐标最接近的观测点为p3，以此可以判断出我们的错误角为观测点P3所在的位置。

（2）错误边查找结果。我将P4-P5点的平距从100.07改到200，我们可以从程序运行的结果中看到，坐标方位角97.3°与我们算出来的结果最为接近，而与坐标方位角97.3°相乘的就是观测点P4到P5的平距。

为了较为全面的测试软件程序的有效性，陆续修改了其他位置的数据还有其它一些教科书上的数据进行测试，所有测试结果都达到了预期的效果。

通过人工计算来校验程序计算结果的时候我们就能发现边角错误的计算确实是一件相当复杂且繁琐的工作，而且容易发生计算错误。但是对于计算机来说这个计算量并不大，只需短短1-2秒钟就能完成计算并给出计算结果，大大节省了人力物力。而且计算机给出的结果更加清晰，能帮助我们快速地判别出错误点的位置。

5 结论

本文以导线测量出来的数据为前提设计了一个帮助相关从业者快速查找错误边角的程序，该程序除了能快速判断出错误边角之外还能准确地找出具体的错误位置。在这之前如果工作人员发现了导线测量超限都只能以人工计算的方式来排查错误，或者是使用一些辅助计算的软件来加快完成这项工作，这个计算过程是极其繁琐的，而且哪怕是使用一些辅助工具来帮助计算，依旧有可能会出现计算错误等问题从而导致无法准确找出错误点的位置，使得错误点增加，反而加大了工作量，导致事倍功半。然而本文设计的这个程序可以有效地解决这个问题，使得原本繁杂的工作过程变得极为简单，只需把数據输入程序中就可能轻松地找到错误点，对于从事相关工作的人来说是非常便利的工具。

——————————

参考文献：

〔1〕赵普分.甲乌拉矿区井下控制导线测量方案的设计与实施[J].地矿测绘，2018，34（01）：41-44.

〔2〕熊鹏飞，朱美燕.无定向支导线控制测量新方法研究[J].内蒙古煤炭经济，2017，9（12）：151-152.

〔3〕莫登华，金炎平，胡智军.导线测量错误的检验及处理方法[J].人民长江，2003，34（06）：46-48.

〔4〕崔利，武文波.测绘领域中MATLAB的应用[J].辽宁工程技术大学学报，2005，24（S1）：47-49.

〔5〕孙庆华，熊伟，张宪柱.基于Excel和MATLAB的导线网平差[J].北京测绘，2009，30（04）：24-26.

〔6〕薛志勤，张宝利.基于AutoCAD的导线测量计算[J].技术与市场，2017，24（08）：88-89.

〔7〕张莹莹，郑建功，赵锋.基于开源框架的WebGIS设计与实现[J].测绘与空间地理信息，2013，36（12）：206-208.

〔8〕李仁刚，任智新，黄广奎，孙颉，王峰，张闯.面向数据库查询加速的异构体系结构设计与实现[J].计算机工程与科学，2020，42（12）：2169-2178.

〔9〕武汉大学《测量学》编写组.测量学[J].3版.北京：测绘出版社，1991.

〔10〕王婷，张磊.导线测量中坐标方位角的推算[J].测绘与空间地理信息，2020，43（12）：35-37.

〔11〕王旭华.查找导线测量错误方法的进一步探讨[J].大连大学学报，2002，23（06）：68-72.

〔12〕刘大文.解析法查找井下导线测量中测角错误[J].煤炭科技，2017，9（03）：34-36.

〔13〕杜福南.浅议井下导线测量中图解法查找测角错误[J].能源与节能，2016，37（09）：34-35.

〔14〕唐芝青，唐先龙.地理空间数据库技术分析与选型[J].测绘与空间地理信息，2020，43（11）：79-81.

〔15〕周忠.数据起源技术研究及其在PostgreSQL中的实现[D].华南理工大学，2016.4-5.

〔16〕Chrzanowski， A.& G.Konecny， 1965. Theoretical comparison of triangulation， trilateration and traversing. The Canadian Surveyor， 19（04）：353-366.

收稿日期：2022-11-14

基金项目：福建省自然科学基金（2020J01262）