常微分方程课堂教学改革的探索与实践

2023-05-30李姝敏郭鹏云徐国明

赤峰学院学报·自然科学版 2023年3期

李姝敏　郭鹏云　徐国明

摘要：常微分方程课程是数学与应用数学专业的一门基础专业课，在师范生核心能力培养中具有重要的作用。基于“四个回归”重要思想，“立德树人”的人才培养目标，“以学生为中心”的教学理念及“两性一度”金课的建设标准以及传统教学中存在的主要问题，本文从课程的教学模式、教学方法和手段、教学内容、考评方式、课程思政等方面对常微分方程课堂教学进行探索与实践。创造性的提出“五步三导”的线上线下混合教学模式，重视课程思想方法的来源与实质，建立多层次、动态、开放的评价体系，挖掘思政元素，建设网上课程资源。

关键词：常微分方程；“五步三导”线上线下混合教学模式；立德树人

中图分类号：G642.0 文献标识码：A 文章编号：1673-260X（2023）03-0088-05

1 引言

常微分方程是师范专业认证下高等学校数学专业核心课程，也是高校中其他理工科高等数学必修内容之一。它以物理、化学、生物等为背景，以数学分析、高等代数为基础的一门课，是进一步学习数学建模、计算方法、孤立子、混沌等延伸课程的基础，是数学理论联系实际的桥梁之一。广泛应用于物理、医疗、交通、航天航空等领域。2016年，习近平总书记在全国高校思想政治工作会议上讲话，作为高校教师，不仅仅要传授知识，还要挖掘课程思政元素，要立德树人。2017年10月教育部开始进行师范类专业认证[1]和提出“以学生为中心”的理念。2018年6月教育部在新时代全国高等学校本科教育工作会议提出“四个回归”[2]重要思想。2018年11月，教育部高等教育司吴岩司长在第十一届“中国大学教学论坛”上，明确提出“两性一度”的金课标准。而常微分方程作为数学类师范专业核心课程之一，要聚焦知识、素养和能力的培养。由此，项目团队开始对常微分方程的教学内容、教学模式、教学手段、考评方式开展探索与实践。

2 常微分方程课堂教学中存在的问题

2.1 课程内容重理论，轻应用，缺乏高阶性

传统课堂局限于讲方程的特点和解法，即知识的传授。如最简单的变量分离方程dx/dt=-kx，每个同学都会求解，而实际问题“碳-14衰变速度与它目前含量成正比”，学生几乎不会列出方程，那么该方程的背景“碳-14定年法”及如何利用方程的解来推断古代文物的历史年代，就是渴望不可求了。可见，学生应用所学知识解决实际问题的能力不足，即课程内容缺乏高阶性。

2.2 教学模式与信息化技术脱离，缺乏创新性

在传统教学模式中，“以教师为中心”，“黑板+粉笔”，没有信息化技术相融合，不能满足新时代大学生对知识的需求。教学内容由一般到特殊，一些知识点学生很难理解和掌握，并缺乏前沿性和时代性。即教学模式和教学内容缺乏创新性。

2.3 考评方式单一，缺乏挑战度

考评方式有些单一，考评点只是知识的考核，而应用能力、实践能力、开放性的题目几乎没有，同学之间没有明显的竞争；另外，学生缺乏课程反思和团队合作意识。即学生的考核缺乏挑战度。

2.4 科学素养，课程思政融入不够，缺乏育人元素

传统教学中，以传授知识为主，淡化课程思想和文化的引领。学生对所学课程，不明白为什么学，学对今后有什么用处，课程思政元素不知如何挖掘与融入，即课程缺乏“育人元素”。

3 常微分方程课堂教学课程改革的思路和方法

3.1 基于学习通平台，提出了“五步三导”的线上线下混合教学模式

为了建立微分方程与生活实际紧密的链接，我们对于传统的微分方程教学设计做了适当调整，创新性的提出“五步三导”的教学设计。即课程以引模型、析模型、解问题、评思维、善運用这五步来构建，以数学建模思维运用、解决实际问题、促毕业促就业为导向，打造以学生为中心、从生活中来到生活中去的良性闭循环的常微分方程课堂。

同时，依托学习通平台，“五步三导”的教学设计，实现线上线下混合式教学模式（图1）。“五步三导”的线上线下混合教学模式的实施，实现了理论与实践的有机融合，使学生在学习知识的同时也学会了解决实际问题的思维与方法，实现了课程的高阶性和教学内容的创新性。

3.2 重视课程的思想方法，优化课程内容

依据“五步三导”的教学设计，对教学内容进行知识点拆分与优化，采用层次化教学，由具体到抽象，由特殊到一般。

第二、四、五章方程（组）的引入、认知、解法、巩固、延伸是“五步三导”的教学设计，是闭循环的教学课堂。重视常微分方程理论与实践的融合，让学生不仅会解方程，还要会解决简单的实际问题。下面以“一阶隐式微分方程”为例。

例：1696年，约翰伯努利向整个欧洲发起了挑战，提出一个数学问题：在垂直平面内有任意两点，一个质点受地心引力的作用，自较高点下滑至较低点，不计摩擦，问沿着什么曲线下滑，时间最短？这个问题就是著名的“最速降线问题”（图2），同时代牛顿、雅各布伯努利、莱布尼茨、洛必达等都给出了正确的结果，伽利略认为是一段圆弧后来被证明是错误的，到底是怎样的曲线呢？

引模型：课前预习。学习通发布“预习清单+视频+章节测试”，学生对本次课内容有初步的了解。对数学问题的模型知识可以查阅资料，提出预习中问题，让学生带着问题进课堂。

析模型：建立模型。观看一个网上“最速降线问题的实验”，学生可以直观验证预习的结论。同时，通过分析数学模型，引出新的知识“一阶隐式微分方程”。

解问题：以抢答的形式，学生列出方程的类型，求解的思想方法，即求解方法（图3），同时提出预习中遇到的问题，强调方法，并以实例进行说明，学生课上进行随堂练习，最后利用所学知识解决最速降线问题（图4）。

评思维：总结本节课的重点内容，同时融入课程思政。2018未来新经济高峰论坛中，宝沃汽车集团杨嵩，利用“一个数学公式代表了宝沃模式”，即利用“最速降线问题”的曲线展示宝沃集团探索中国力量崛起的模式（图5）。该问题给我们的启示是，要好好规划化自己的人生，路径长的用时未必长。同时，要有爱国精神，文化自信，努力学习为我国科技领先全球未来尽微薄之力。

善运用：观看“2018年全国高等学校数学微课”视频片段，学生可以深入理解最速降线问题在实际生活中的应用，体会数学之美，数学之魅力。并且提出新的问题（图6），第二章都是利用初等积分法求微分方程的解析解，那是不是所有微分方程都可以利用初等积分法求解呢？如果不能，又该如何判定和求解呢？引出下节课内容。

第三章是理论性最强最难的一章，拆分成四个知识点配思维导图，思路清晰，内容环环相扣，层层递进，学生的学和教师的教变得容易多了。如，解的存在唯一性定理的命题3证明比较难，做思维导图（图7），学生就可以很清晰知道每一步的目的和采用的方法。

第四章中高阶微分方程的常数变易法，采用特殊到一般的方法。将一阶推广到二阶后巩固练习，引导学生推广到三阶，直至到n阶，并利用代数理论将其公式化，层层递进。

在教学中注重“数学建模的思想”“变量替换的思想”和“常数变易的思想”的引领，让学生了解思想的来源、抓住思想的本质，从而理解和应用其他思想方法。通过该课程的教学，进一步培养了学生的学科思想，从而实现该课程的理论创新和实践创新。

3.3 建立多层次、动态、开放的考评方式

基于“以学生为中心”的理念，依托学习通平台，考评方式（图8）实现对学生的课前、课中和课后进行全方位的监督和引导。

课前考核：学习通上，发布预习清单，设置预习任务点，引导学生预习视频，完成章节测试，并完成问题清单，提出预习中的问题。根据平台数据及时了解学生预习的进度和知识点的理解程度。让学生和教师带着目标进课堂。

课中考核：展示上节课或往届作业，发现问题、讨论更正问题。强调关键点，如第二章是“两要一不要”，即要“变量还原”，要“画龙点睛”，不要“画蛇添足”；培养学生的明辨性思维，加入了育人元素。此外学习通进行随堂练习，教师随堂点评问题，有问题随时改正，同时鼓励又快有准确的同学，也鼓励进步的同学，让学生要有公正的意识。

课后考核：作业+小组讨论+课程反思与实践。作业，上传学习通，做得好的评出部分优秀作业，共性问题的，在课上学生共同纠错（图9）。课后小组讨论基于重点知识点，发布一些难度大的题，学生在腾讯会议中进行讲解（图10）、讨论，将文档和视频上传学习通“PBL分组任务”中，实行组内、组间和教师评价；课程反思实践（图11）要求以思想方法为主线，对常微分方程的课程内容进行宏观和微观的总结与归纳，并在期末前完成。而这两项对于学生具有一定的挑战度。

依托学习通平台，线上线下多层次、动态、开放的考评方式，有点有面、强化了知识内容，培养了学生的表达能力、运用知识解决实际问题的能力及团队合作意识，提高了学生的师范技能和学习的自信心，为学生将来从事教学及相关管理工作打下扎实的基础。

3.4 如盐入味、点滴融入思政元素

与传统教学模式相比，“五步三导”的线上线下混合教学模式更易于课程思政与教学内容的有机融合。我们主要从“讲述科学家的励志故事”和“典型案例”两个方面融入课程思政。

常数变易法，是法国数学家拉格朗日歷经11坚持不懈探索的成果，激励学生要有坚持不懈、不急于求成、勇于探索的精神。学习欧拉方程和欧拉公式时，介绍大数学家欧拉[3]的生平，他是在黑暗中给人类带来光明的人，他提出的“宇宙第一公式”，让学生了解其中的内涵，懂得健康的美好，生活的美好，努力前行！

学习变量分离方程，引入典型案例“他是嫌疑犯吗”，引导学生学会科学处理问题的方法，凡事要有据；学习伯努利方程时，利用典型的逻辑斯蒂方程建模，求解，画图拟合“江苏扬州”新冠肺炎确诊病例的增长趋势散点图，让学生明白发现疫情是可防可控的，作为大学生我们要遵守学校要求，封校期间非必要不外出，戴口罩，不信谣不传谣；致敬我们的英雄，向他们学习，做一名有责任、有担当的爱国大学生。学习一阶隐式微分方程时，引入“最速降线问题”[4]。学生通过建模，认识“一阶隐式微分方程”的类型及解法，并且利用微分方程的解解释最速降线问题，介绍它与旋轮线的关系，在实际生活中的应用，让学生感受数学之美，数学之魅力。

这样将育人元素点滴融入，穿针引线、潜移默化之中影响到学生的身心。鼓励学生成为有理想信念、有爱国情怀、有扎实学识、有仁爱之心的好老师，且做事情要有严谨的态度和科学处理问题的方法，逐步成为全面发展、持续发展的社会栋梁。

3.5 建设网上课程资源

基于“五步三导”教学设计，分解知识点，制作PPT课件，由团队教师录制知识点视频48个，配相应章节测验、作业、单元测试[5]，于2021年8月在学银在线实现在线开放（表1）。结合网上资源，本校学生初步实现线上线下混合式教学，实现师生实时互动、互评。

4 常微分方程课堂教学改革的效果

4.1 教书育人于一体

立足建模思想的常微分方程课程教学，集案例法和任务驱动法于一体，提高了学生的学习兴趣，启发了学生利用所学知识解决实际问题的思维，培养了学生灵活运用知识的能力[6]。“五步三导”的线上线下混合教学法的应用，让数学问题从实践中来，然后到实践中去。循环往复，生生不息。而且容易将课程思政融入课堂，达到教书育人的目的。这对于培养学生科学理智处理问题形成正确的世界观、人生观、价值观是非常有效的。

4.2 课程目标达成度明显提高

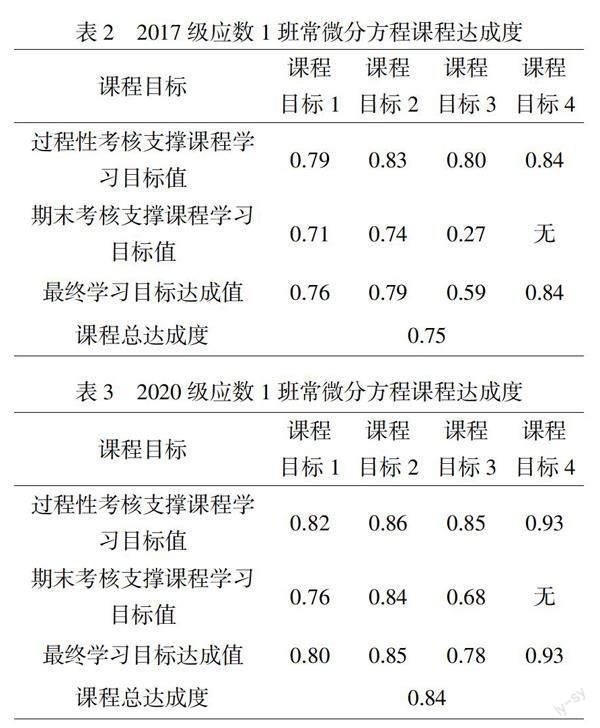
期末试卷中，2020级应数1班（表3）比2017级应数1班（表2）常微分方程试题难度增大、题量增大、覆盖面更广，但是课程的达成度却有所提高，课程目标3，理论的应用尤为明显，这与课程设计和教学方法是分不开的。

4.3 教学质量评价

近几年，任课教师的教学质量评价也在稳步上升。2021年秋季，2020应数1班首次基于录制视频实现线上线下混合式教学，考评方式加入“课程反思与实践”，学生对课程给出高度评价，教学质量评价为98.02分，也对课程的线上资源给出肯定的评价。

5 结语

在已经到来的“师范专业认证”的背景下，“以学生为中心”的理念已经得到充分的贯彻，常微分方程课程教学改革已经从教学理念、教学内容、教学手段、教学评价等方面做了有益的探索和实践，很好地诠释了“以学生为中心”的学生态度、情感、科学素养的全面发展理念，为适应新时代的应用创新型人才培养目标提供了强大的动力。

——————————

参考文献：

〔1〕李晨松.基于师范专业认证的常微分方程教学模式改革探究[J].内蒙古民族大学学报，2021，36（02）：171-174.

〔2〕侯利元，和平.“四个回归”背景下常微分方程的教学改革[J].高师理科学刊，2019，39（08）：79-82.

〔3〕陈光霞，李凤萍.课程思政理念在《常微分方程》教学改革中的应用[J].高等数学研究，2022，25（01）：101-104.

〔4〕王高雄，周之铭，朱思铭，王寿松.常微分方程（第四版）[M].北京：高等教育出版社，2020.