认知心理学视角下数学概念的教学实践与思考
2023-05-30赖小敏于涛
赖小敏 于涛


[摘 要] 文章以认知心理学的理论为指导,从认知过程、概念表征、学习迁移等角度对“充分条件与必要条件”进行了教学分析,呈现了教学实施过程,总结了两点促进认知结构构建的教学思路.
[关键词] 认知心理学;概念;充分条件;必要条件
概念是一类事物共同的本质属性,是反映一类事物本质属性的表征. 文[1]从数学概念的获得、结构分析、表征、认知模式等角度分析了数学概念学习的认知理论,揭示了概念学习的特殊性与复杂性. 从认知心理学的角度来看,数学学习会经历“数学现象—心象—抽象—操作”的认知过程[2],如何准确把握学生的认知基础,帮助学生有效构建认知结构,一直是概念教学的热点问题. 下面以“充分条件与必要条件”为例,探讨遵循学生认知规律的教学思路.
教学分析
“充分条件与必要条件”是人教A版必修第一册(2019年版)第1章第4节第1课时的内容,本课以“若p,则q”形式的命题为载体,通过考察命题中条件p与结论q的关系,学习充分条件、必要条件等常用逻辑用语. 教材编写以比较容易判断真假的命题为例子,意在突出学习重点是对充分条件、必要条件的意义的理解和辨析,以避免判断命题的真假成为学生学习本节内容的障碍. 在具体的教学实践中,有以下几个教学问题值得探讨.
1. 遵循从现象和心象到抽象的认知过程
数学概念源自生活现象,在生活实践与学习的过程中,学生通过感知生活现象,在头脑中形成各种对生活现象的直观认知,即“心象”,通过对心象的积累与理性分析等过程,逐步在归纳、概括后抽象得到概念. 教学如果直接跳过生活实践中的数学现象,以“若x2-4x+3=0,则x=1”“若平面内两条直线a和b均垂直于直线l,则a∥b”等命题作为例子展开教学,学生更多在明确命题“若p,则q”的条件p与结论q,以及命题真假判断的基础上,接受充分条件、必要条件等数学“名词”,机械地记忆与应用这些数学知识. 教学有必要联系日常的生活实际,增强例子的直观性,让概念学习从数学外部的生活过渡到数学内部的概括抽象,引导学生经历完整的认知过程.
2. 借助不同的概念表征来深化概念理解
表征本质上是被表征对象的替代[3]. 当学习者看到某个概念后能想到的东西就是这个概念的表征. 例如“北京”,其表征可能是“首都”“天安门”“长城”“北京烤鸭”等. 要让学生更好地理解某个数学概念,就需要帮助学生从言语化、视觉化等不同表征形式来理解同一个数学学习对象. 在以符号“p⇒q”和文字“p是q的充分条件,q是p的必要条件”等概念表征组织教学的基础上,不妨借助“集合”等表征形式帮助学生更好地理解概念. 认知心理学认为概念学习分两种形式,一种是概念形成,是学习者从大量的同类事物的不同例证中发现其共同的关键性的本质特征而获得概念;另一种是概念同化,或称概念掌握,是学习者从自己的认知结构中原有的有关概念通过同化而获得新概念[4]. 研究者在多年教学实践中发现,只有符号和文字表征的教学,学生容易出现概念理解不深刻、命题真假判断困难等学习问题,教学可以从集合的角度通过概念同化,深化概念理解,更好地沟通新知与旧知的联系,构建认知结构. 此外,还可以借助判定定理与充分条件、性质定理与必要条件之间的关系来帮助学生理解新知,这也是新教材编写的变化之处.
3. 通过调整教学顺序促进学习迁移发生
充分条件、必要条件是对“若p,则q”形式命题的条件与结论辩证关系的学习,组织教学围绕“若p,则q”形式命题的真假判断而展开. 传统教学观念下的教学注重“双基”落实,教学通常将真命题、假命题的例子混在一起,课堂教学演练操作多,自主探究思考少. 为实现新一轮课程改革的教学理念,培养学生从“学会”到“会学”,教学时不妨将真命题、假命题的例子分为不同的组:首先,师生共同用真命题的例子完成充分条件、必要条件的学习;其次,学生在前面学习的基础上进行学习迁移,用假命题的例子自主完成“不是充分条件、不是必要条件”的学习. 后续充要条件的教学也可以进行类似的教学顺序优化,促进学生学习迁移的发生.
教学实践
1. 概念形成
在日常生活和数学学习中,我们经常可以看到“若p,则q”形式的命题,其中p称为命题的条件,q称为命题的结论.
引例 若我是东莞人,则我是广东人.
问题1:(1)这个命题的条件和结论是什么?(2)判断这个命题的真假.
生1:条件是“我是东莞人”,结论是“我是广东人”.
生2:因为东莞市在广东省内,所以该命题是真命题.
师:对于上述真命题,我们用数学符号“⇒”进行等价表述:“我是东莞人”⇒“我是广东人”. 其中,“我是东莞人”可以“充分”地说明“我是广东人”. 我们用逻辑用语表述为:“我是东莞人”是“我是广东人”的充分条件.
追问1:若我是广东人,那么我一定是东莞人吗?
生3:不一定,我可能是廣州人,也可能是深圳人,等等.
师:也就是说,我是东莞人,前提是我是广东人;如果我不是广东人,那么我不是东莞人. 所以“我是广东人”对于“我是东莞人”而言是必不可少的,是必要的. 我们用逻辑用语表述为:“我是广东人”是“我是东莞人”的必要条件.
师生对话的同时,教师板书:“‘若我是东莞人,则我是广东人’是真命题”及其三种等价说法,分别为①(符号语言)“我是东莞人⇒我是广东人”,②(逻辑用语)“我是东莞人”是“我是广东人”的充分条件,③(逻辑用语)“我是广东人”是“我是东莞人”的必要条件.
教学中,教师引导学生再列举一些具体命题的例子,进而概括抽象形成新的数学概念:
一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,记作p⇒q,称p是q的充分条件,q是p的必要条件.
设计意图 教学从生活现象到数学概念,引导学生经历从现象到心象再到抽象的学习过程. 引例的设计“一例双关”,一方面用生活实例呈现命题“若p,则q”,借助生活现象中的逻辑判断,通过师生对话引导学生体会“充分”与“必要”的生活含义,进而在生活现象的理解基础上进行概括抽象,初步完成充分条件和必要条件概念的学习,并借助“‘若p,则q’为真命题”“p⇒q”“p是q的充分条件”“q是p的必要条件”这四种等价说法从推理的角度强化理解概念;另一方面,该生活实例直观地用地图(广东省地图)呈现,既能帮助学生直观感知生活现象,又能从集合的角度为新知学习做好铺垫.
2. 概念同化
问题2:从集合的角度研究命题“我是东莞人,则我是广东人”,其条件和结论对应的集合分别是什么?并说出两个集合的关系.
生4:条件对应集合{东莞人},结论对应集合{广东人}.
生5:条件对应的集合{东莞人}是结论对应的集合{广东人}的子集.
师:用集合语言将命题改写为“若x∈{东莞人},则x∈{广东人}”,显然,由{东莞人}⊆{广东人}可判断命题“若x∈{东莞人},则x∈{广东人}”是真命题. 也就是说,由{东莞人}⊆{广东人}(集合的包含关系)可得:“我是东莞人”是“我是广东人”的充分条件和“我是广东人”是“我是东莞人”的必要条件.
追问2:对于命题“若p,则q”,你能否从集合关系的角度理解充分条件和必要条件?
生6:若“条件p对应的集合”是“结论q对应的集合”的子集,则命题为真命题,p是q的充分条件,q是p的必要条件.
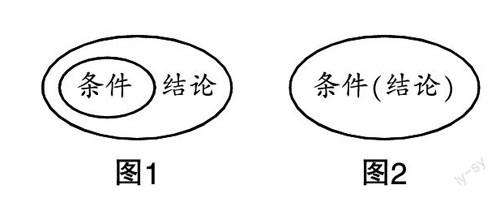
教师在学生直观感知的基础上,用集合语言表述:记A={x
x满足条件p},B={x
x满足结论q},当A⊆B时,“若p,则q”是真命题,p是q的充分条件,q是p的必要条件. 同时,借助图1、图2帮助学生深化理解.
[结论][条件][图1][图2] [条件(结论)]
设计意图 当学生有了充分条件和必要条件的知识后,引导学生从集合的角度理解充分条件和必要条件的内涵. 一方面丰富概念的表征,在符号、语言等表征的基础上增加图形表征;另一方面利用学生认知结构中原有的集合知识同化逻辑用语的知识,沟通旧知和新知之间的联系与区别,实现概念同化. 以此帮助学生积极主动地构建与完善自身的认知结构,积累从不同表征来理解概念的基本活动经验.
3. 操作实践
例1 判断下列“若p,则q”形式命题的真假,用其他三种等价说法描述这一逻辑关系,并从集合的角度进行解释.
(1)若a=b,则ac=bc;
(2)若平行四边形的对角线相互垂直,则平行四边形是菱形;
(3)若两个三角形全等,则两个三角形的周长相等.
设计意图 例1的三个小题均为真命题. 教学中,先引导学生从逻辑推理的角度判断命题的真假,通过其他三种等价说法强化概念的符号语言与文字语言之间的关系,然后引导学生从集合关系的角度理解新知,感悟对于不同的命题集合表征的理解在思维上具有一致性. 从引例到例1,引导学生经历“数学现象—心象—抽象—操作”完整的认知过程,为围绕假命题展开学习做好类比迁移、自主学习的准备.
4. 类比迁移
例2 判断下列“若p,则q”形式命题的真假,仿照例1用其他三种等价说法描述这一逻辑关系.
(1)若x2=1,则x=1;
(2)若四边形是梯形,则该四边形是平行四边形;
(3)若四边形是菱形,则该四边形是矩形.
(学生思考作答,教师点评板书)
问题3:仿照“真命题”的情形概括“假命题”逻辑关系的一般性表述.
生7:一般地,“若p,则q”为假命题,是指由p通过推理不能得到q,记作p[⇒] q,称p不是q的充分条件,q不是p的必要条件.
设计意图 例2和问题3构成了有机整体,教学中,引导学生类比“真命题”的学习,开展关于假命题“不是充分条件”和“不是必要条件”的学习,再次经历“心象—抽象—操作”的认知过程,培养学生自主学习的能力与意识.
活动:请仿照前面的活动经验,从集合的角度解释例2中各命题的逻辑关系.
学生进行小组活动,教师观察指导.当学生得到例2三个小题的集合图示分别对应图3、图4、图5后,教师帮助学生从集合表征的角度判断假命题,理解“不是充分条件”和“不是必要条件”的内涵. 类比真命题的教学过程,总结并概括出:对于命题“若p,则q”,当“条件p对应的集合”不是“结论q对应的集合”的子集时,“若p,则q”是假命题,p不是q的充分条件,q不是p的必要条件.
设计意图 例2的三个小题均为假命题,分别对应不同集合关系的图示,这三种集合关系的图示(图3、图4、图5)与前面两种集合关系的图示(图1、图2)刻画了条件与结论对应集合的所有可能,意在让学生在类比学习的过程中,通过积极构建逐步形成完整的認知结构,内化对新知的理解.
5. 综合演练
练习1:判断下列命题的真假.
(1)“两个三角形相似”的一个充分条件是“两个三角形的三边成比例”;
(2)“实数x>0,y>0”的一个必要条件是“xy>0”.
练习2:写出“四边形是平行四边形”的一个充分条件和一个必要条件.
设计意图 练习1在学生理解概念的基础上,突出强调对命题的条件和结论的辨识,再强化从逻辑推理和集合关系两种角度判断充分条件和必要条件的方法技能;练习2以开放题的形式引导学生回顾与平行四边形有关的判定定理和性质定理,理解每一条判定定理都给出了相应数学结论成立的一个充分条件,每一条性质定理都给出了相应数学结论成立的一个必要条件[5],丰富新知概念表征的同时,继续完善认知结构.
教后思考
认知心理学理论认为,知识是通过认知主体的积极建构而获得的,而不仅仅是通过传递而实现的[6]. 知识传递的教学以教师讲授为主,学生的学习处于被动接受、记忆、理解的状态,教师在教学设计时更关注微观的课时教学目标,例如要落实哪些知识点,以及哪些方法题型等,教学呈现“自上而下”的状态,以教师头脑中知识的认知呈现为主;知识构建的教学以学生为学习主体,知识学习是通过学生积极构建获得的,教师在教学设计时更关注学生如何学,包括知识体系的构建、学习能力的培养等,教学呈现“自下而上”的状态,通過引导学生经历完整的认知过程,对新知进行有意义的构建,或者对原有认知结构进行改造.
那么,如何设计促进学生建构认知结构的教学思路呢?笔者有两点感悟:
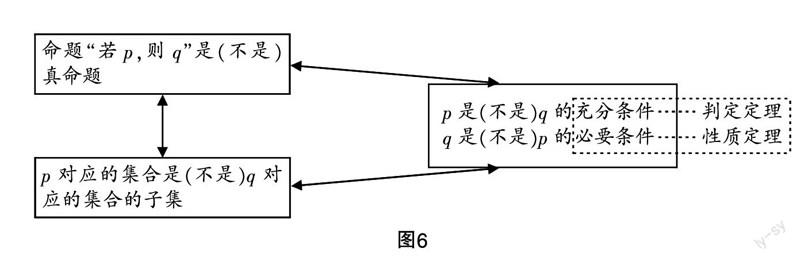
第一,要构建概念表征的图式.文中案例实践之前,笔者尝试构建了“命题的真假”“集合的子集关系”“判定定理和性质定理”等学生已有的知识与“充分条件和必要条件”等新知的关系图式(如图6所示),借助此图式组织教学,先后从不同的角度帮助学生内化新知,建立概念对象,并以此图式作为教学的隐性目标,促进学生概念域的形成. 对概念图式的把握,能有效帮助教师调整教学目标,提高学生的学习效率.
第二,要创造学习迁移发生的机会.文中案例将概念图式(图6)拆成了两个图式,先学习“是”的情形,让学生积累新知学习的活动经验,再学习“不是”的情形,让学生把新知纳入已有的知识经验系统中. 学习迁移的发生,能促进学生在模仿的过程中,自主经历感知、辨别、激活、内化、应用等学习过程,主动构建,有助于学生理解概念的内涵,使得学生不仅知识数量逐渐增加,知识质量也发生变化(知识得到重组).
总之,高中数学教学有待更多的一线教师关注认知心理学与数学教育,让教学更加符合学生的认知规律.
参考文献:
[1] 梁英. 基于认知心理学理论的数学概念教学分析[J]. 广东技术师范学院学报,2006(04):102-104.
[2] 王名扬,徐沥泉,徐利治. 论一种缘自认知心理学及教育学研究的数学认知过程[J]. 数学教育学报,2013,22(01):33-36.
[3] 唐剑岚. 概念多元表征的教学设计对概念学习的影响[J]. 数学教育学报,2010,19(02):28-33.
[4] 曾玖红. 从认知心理学角度论微分概念的教学[J]. 数学教育学报,2012,21(04):76-78.
[5] 人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心. 普通高中教科书:数学必修第一册[M]. 北京:人民教育出版社,2019.
[6] 谢明初,朱新明. 认知心理学视角下的数学教育[J].数学教育学报,2007(01):12-16.
