高中两版数学教材“平面解析几何”习题与课程标准修订版的一致性分析
2023-05-30苏咪咪马旭
苏咪咪 马旭






[摘 要] 文章基于核心素养,对人教版和北师大版两版高中数学教材“平面解析几何”习题与《普通高中数学课程标准(2017年版2020年修订)》(简称课程标准修订版),从总体水平、“平面解析几何”单元内容主题维度、认知水平维度进行一致性比较分析,研究发现不同维度下两版高中数学教材习题与课程标准的一致性各有差异,总体而言,人教版习题与课程标准修订版的一致性高于北师大版.
[关键词] 核心素养;课程标准;高中数学教材;平面解析几何;一致性
问题提出与研究价值
高中数学课程是义务教育阶段后普通高级中学的主要课程,具有基础性、选择性和发展性[1]. 课程理念的第一条便明确指出“学生发展为本,立德树人,提升素养”[1]. 《普通高中数学课程标准(2017年版2020年修订)》(简称课程标准修订版)的发布标志着新一轮的基础教育课程改革进入了全面深化阶段[2]. 由于习题是教材的重要组成部分[3],在该形势下,高中数学教材的习题与课程标准的一致性很有必要研究. 通过查阅文献发现,关于高中数学教材的习题与课程标准修订版的一致性研究较少,本文基于核心素养,对人教版(2019年)和北师大版(2019年)两版高中数学教材“平面解析几何”习题与课程标准的一致性进行比较分析,可以了解课程标准在两版高中数学教材“平面解析几何”习题中的一致性特征和落实情况;对今后我国深化课程标准和高中数学教材及习题的研究和修订提供参考性的意见[4];极大地丰富高中数学教材的习题与课程标准修订版的一致性研究.
研究设计
1. 研究对象
本文以课程标准修订版以及人教版(2019年)和北师大版(2019年)两版高中数学教材“平面解析幾何”的课后习题为研究对象,以量化研究为主,质性研究为辅,对两版高中数学教材“平面解析几何”习题与课程标准修订版从总体水平、内容主题维度、认知水平维度进行一致性比较分析.
2. 研究工具
(1)SEC一致性分析模式
SEC一致性分析模式是帕特等人对韦伯一致性分析模式做了一定程度的改进后,开发并研制出学业评价和课程标准一致性水平分析程序和方法,该模式保留了一致性最核心的内容主题和认知水平两个维度来构建其研究矩阵[5],更加直观简洁,是研究教材习题与课程标准修订版之间的一致性显著程度的重要路径,其具体的分析程序和方法如图1所示.
Porter(帕特)一致性系数的计算公式为P=1-. 其中,n表示二维矩阵中单元格数量,Xi和Yi分别表示X矩阵和Y矩阵中第i个单元格的比率值,P表示Porter一致性系数,取值范围是0≤P≤1,P的大小表示评价内容与课程标准内容两者一致性吻合程度,P=0表示两者一致性吻合程度最低,P=1表示两者一致性吻合程度最高,即Porter一致性系数P值与一致性吻合程度成正比关系,P值越大,一致性就越高[6].
(2)核心素养评价框架
喻平教授提出了一种数学核心素养划分的理论构想:将数学知识学习分为3种形态,依次为知识理解、知识迁移和知识创新. 为学生学科核心素养的评价提供了一个理论框架,即数学核心素养评价的一个框架[7].
3. 研究过程
(1)对“平面解析几何”单元的内容主题的划分与编码
根据课程标准修订版将两版高中数学教材“平面解析几何”内容划分为三个内容维度,分别为“直线与方程”“圆与方程”和“圆锥曲线与方程”.
(2)对认知水平的划分与编码
依据喻平教授提出的数学核心素养评价的一个框架将认知水平划分为知识理解、知识迁移和知识创新,将其依次编码为1,2,3;由于两版高中数学教材“平面解析几何”内容只涉及数学抽象、逻辑思维、数学建模、直观想象和数学运算这五个数学核心素养,所以认知水平只针对这五个数学核心素养进行分析,将其依次编码为A、B、C、D、E. 因此,A1代表数学抽象核心素养的一级认知水平,A2代表数学抽象核心素养的二级认知水平,以此类推.
(3)对课程标准修订版中“平面解析几何”单元的内容要求的编码
根据课程标准修订版以及喻平教授对认知水平的划分和具体阐述,将认知水平与课程标准修订版“平面解析几何”单元的内容要求中出现的动词建立如表1所示的对应表.
确定科学合理的编码原则是有效编码的重要环节,课程标准修订版的编码原则如下:
当“平面解析几何”单元的内容要求中含有多个表1中的动词加名词的条目时,须拆分为多个只含有一个上述动词加名词的条目. 例如把“理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点的直线斜率的计算公式”拆分为“理解直线的倾斜角和斜率的概念”“经历用代数方法刻画直线斜率的过程”和“掌握过两点的直线斜率的计算公式”.
当“平面解析几何”单元的内容要求中某一条目含有多个表1中的动词时,遵循取高不取低的原则. 例如“探索并掌握平面上两点间的距离公式”中的“探索”比“掌握”的认知水平高则取“探索”.
当一个表1中的动词对应多个并列名词时,须拆分并列名词. 例如把“能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系”拆分为“能根据给定直线、圆的方程,判断直线与圆的位置关系”和“能根据给定直线、圆的方程,判断圆与圆的位置关系”.
对“平面解析几何”单元的内容要求进行拆分后所形成的具体的内容要求按照内容主题分别编码为1.1,1.2,…,2.1,2.2,…,3.1,3.2,….
(4)对教材习题的编码
当一道题目中含有分号或几个小问时须拆分;当一道题目中同时考察多个核心素养和认知水平时,以侧重的核心素养和更高的认知水平为准. 根据该编码原则对两版高中数学教材“平面解析几何”单元的习题按照“直线与方程”“圆与方程”和“圆锥曲线与方程”三个主题维度进行排序和编码.
研究分析与结论
1. 两版高中数学教材“平面解析几何”习题与课程标准修订版的总体水平一致性分析
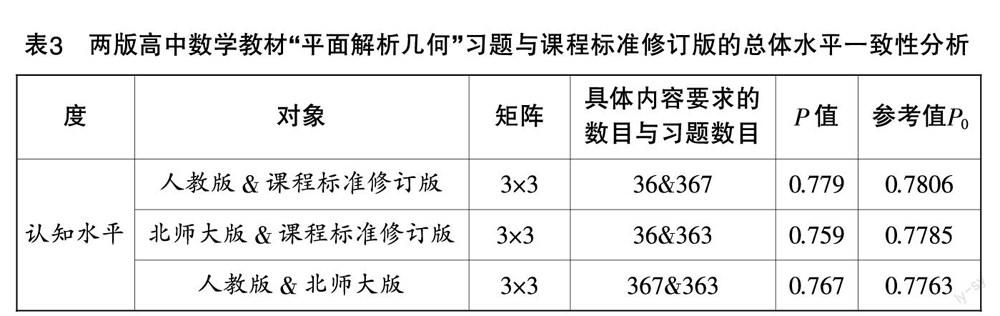
依据上述编码原则统计出课程标准修订版中关于“平面解析几何”单元的具体内容要求数目为36,人教版与北师大版的课后习题数目分别为367和363. 根据上述统计数据建立“内容主题—认知水平”二维矩阵,由于内容主题被划分为三个维度,认知水平被划分为三个水平,所以均建立起“3×3”的矩阵. 运用MATLAB计算出两个矩阵之间的一致性系数P值,此过程循环往复后获得P值的正态分布曲线,得到统计学意义上0.05水平上的显著性参考值P.比较计算出来的P值与参考值P,若P大于P,则说明两者之间具有统计学意义上的一致性,若P小于P,则说明两者之间不具有统计学意义上的一致性[6].
由表3可知,人教版和课程标准修订版、北师大版和课程标准修订版、人教版和北师大版一致性系数均小于参考值,不具有统计学意义上的一致性. 相对于北师大版的习题,人教版和课程标准修订版的一致性系数更高,说明人教版的习题和课程标准修订版的一致性吻合程度更好.
2. 两版高中数学教材“平面解析几何”习题与课程标准修订版在该单元的内容主题维度下的一致性分析
(1)两版高中数学教材习题与课程标准修订版在“平面解析几何”单元的内容主题维度下的核心素养频率分布
由图2可知,在“直线与方程”内容主题维度下,人教版习题与课程标准修订版的核心素养分布的一致性更高;在“圆与方程”内容主题维度下,相比课程标准修订版,两版高中数学教材习题均增加了数学运算和直观想象两个核心素养,且数学抽象核心素养的比率均高于课程标准修订版,但两版高中数学教材习题在数学建模和逻輯推理这两个核心素养的比率均低于课程标准修订版;在“圆锥曲线与方程”内容主题维度下,两版高中数学教材习题均增加了数学运算和逻辑推理这两个核心素养,关于总比率,北师大版习题与课程标准修订版相差较小,但人教版习题的核心素养分布与课程标准修订版的一致性相比北师大版更高. 总体而言,相比北师大版,人教版习题与课程标准修订版在内容主题维度下的核心素养分布的一致性更高.
(2)两版高中数学教材习题与课程标准修订版在内容主题维度下的认知水平分布
由图3可知,在“直线与方程”内容主题维度下,两版高中数学教材习题与课程标准修订版在知识迁移认知水平的一致性较高,其中人教版习题在知识迁移水平的比率与课程标准修订版几乎吻合,然而两版高中数学教材习题与课程标准修订版在知识理解和知识创新两个认知水平的一致性均不高;在“圆与方程”内容主题维度下,相比北师大版,人教版习题与课程标准修订版在三个认知水平的一致性更高;在“圆锥曲线与方程”内容主题维度下,相比人教版,北师大版习题与课程标准修订版在三个认知水平的一致性更高,吻合度更好. 总体而言,两版高中数学教材习题在知识迁移认知水平与课程标准修订版的要求一致性更高,知识创新认知水平次之,知识理解认知水平与课程标准修订版的一致性有待提高.
3. 两版高中数学教材“平面解析几何”习题与课程标准修订版在认知水平维度下的一致性分析
(1)两版高中数学教材习题与课程标准修订版在认知水平维度下的核心素养分布
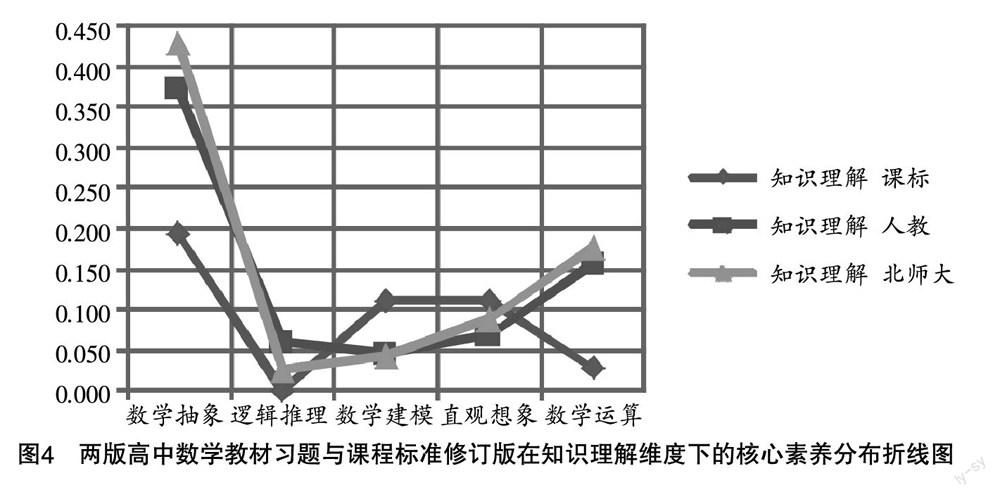
由图4可知,在知识理解认知水平维度下,课程标准修订版侧重培养数学抽象核心素养,两版高中数学教材习题与课程标准修订版的一致性较高;在直观想象核心素养方面,两版高中数学教材习题与课程标准修订版的一致性也相对较高,但对于数学建模和数学运算这两个核心素养,两版高中数学教材习题分别未达标和超标. 从整体来看,在知识理解认知水平维度下,两版高中数学教材习题均与课程标准修订版保持着较高的一致性.
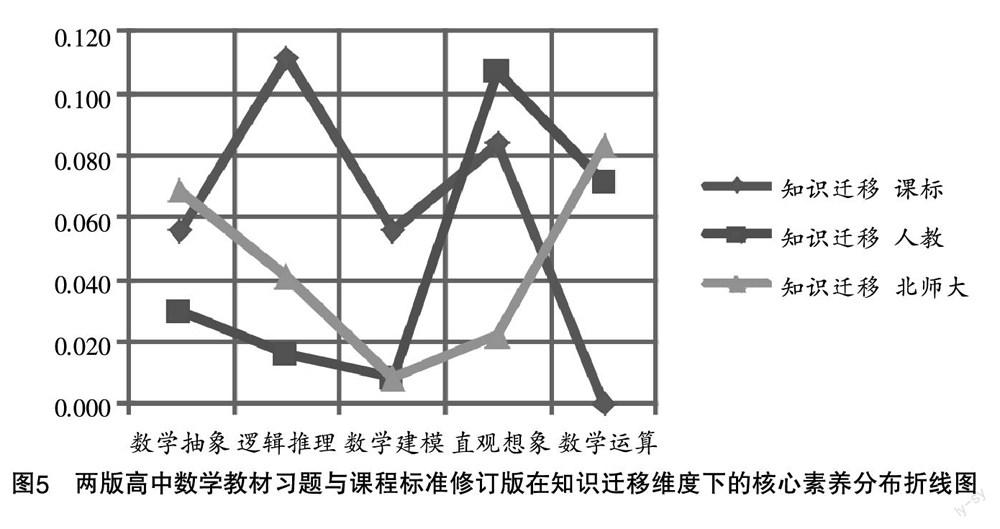
由图5可知,在知识迁移认知水平维度下,课程标准修订版侧重逻辑推理核心素养,然而人教版习题侧重直观想象核心素养,北师大版侧重数学运算核心素养,人教版习题与课程标准修订版在直观想象核心素养的一致性较高,北师大版习题与课程标准修订版在数学抽象核心素养的一致性较高.
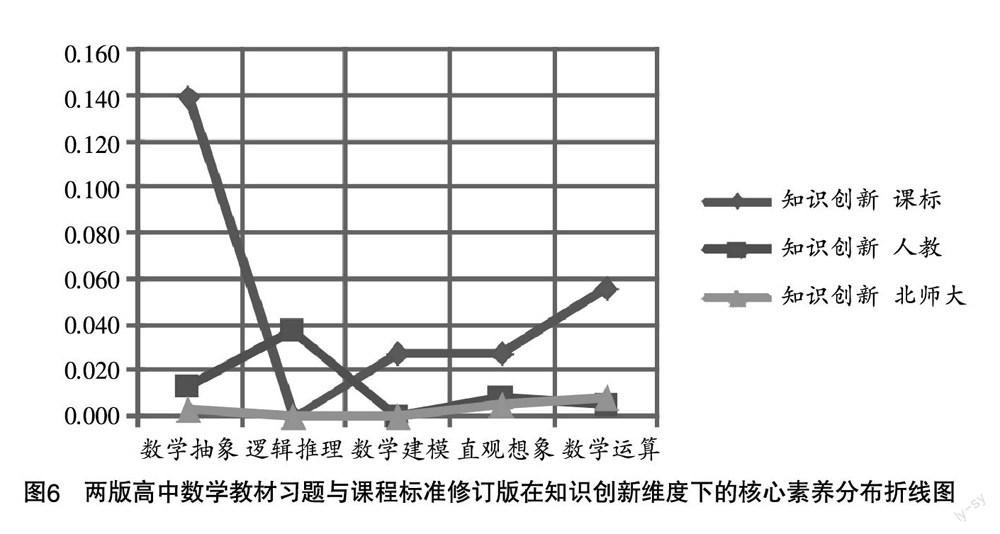
由图6可知,在知识创新认知水平维度下,课程标准修订版侧重数学抽象,人教版和北师大版两版高中数学教材习题对该认知水平的呈现相对较少,两版高中数学教材习题与课程标准在知识创新认知水平下的核心素养分布一致性相对不高.
(2)两版高中数学教材习题与课程标准修订版在认知水平维度下的内容主题分布
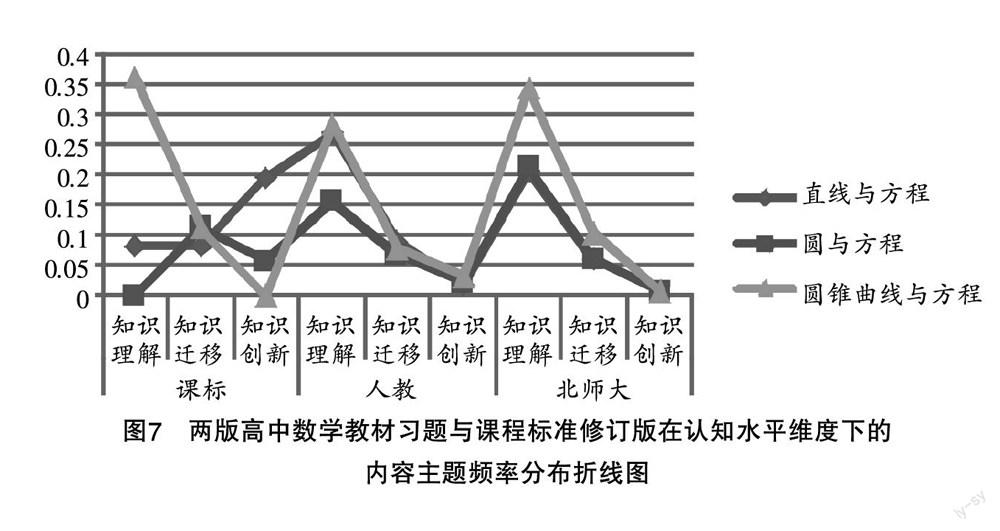
由图7可知,在认知水平维度下,课程标准修订版对于“直线与方程”的内容呈现先持平后增长的趋势,而两版高中数学教材均保持下降趋势;课程标准修订版对于“圆与方程”的内容呈现先增长后减少的趋势,两版高中数学教材均保持下降趋势;课程标准修订版对于“圆锥曲线与方程”的内容呈现持续下降的趋势,两版高中数学教材也均保持下降趋势,与课程标准修订版在内容上的要求保持着较高的一致性.
研究建议
1.教材编写者应以深度理解课程标准修订版为“生成点”,以着力完善教材评价为“脚手架”
教材编写者先要深度理解课程标准修订版的本质,才能站稳第一个“生成点”,随之着力完善教材评价体制,才能真正查漏补缺,充分利用教材评价这一“脚手架”,稳步攀登到更高的“生成点”,建立起动态的良性推进循环,从而实现基于核心素养的高中数学教材习题与课程标准修订版在“量”与“质”方面的高度一致性.
教材编写者深入理解课程标准修订版的本质,一方面需要认真研读课程标准修订版,谨遵课程标准修订版以发展学生数学核心素养为宗旨的要求挖掘其本质与深度;另一方面有赖教材编写的参与者共同努力进而形成合力,从而有质量、有效率地实现教材习题与课程标准修订版的一致性.
完善教材评价体制包括对教材评价的方法手段、标准要求和工具设计等方面的改进,基于我国数学教材评价体制的现实水平和实际需求,借鉴吸收国外修订课程标准和改革课程的有益经验,进一步优化我国教材评价体制.
2.教师把握核心素养分布的均衡性,注重认知水平的循序渐进
上述研究结论表明,核心素养分布在内容主题、认知水平以及总维度上均有差异,不同核心素养下教材习题与课程标准修订版的一致性也各有不同. 因此教材习题应明确各核心素养下的权重,均衡分布各核心素养,促进学生的均衡发展[8]. 关于认知水平,在关注各层次认知水平在不同维度下的一致性分析的同时,也要注重认知水平的循序渐进,认知水平从知识理解到知识迁移再到知识创新呈现阶梯性,那么教材习题关于认知水平的分布也应循序渐进地分布,教师可适当增减相应习题的呈现,把握核心素养分布的均衡性,注重认知水平的循序渐进.
参考文献:
[1] 中华人民共和国教育部.基础教育课程改革纲要(试行)[M]. 北京:人民教育出版社,2001.
[2] 严必友,宋晓平. 体现继承与发展的数学课程目标——解读《普通高中数学课程标准(2017年版)》目标体系[J]. 数学通报,2018,57(12):18-21.
[3] 李爽,杨泽恒,王彭德. 核心素养视角下云南高中学业水平考试和高考数学试卷分析[J]. 数学教育学报,2020,29(06):25-31.
[4] 刘婉悦. 不同版本初中数学教材习题与课程标准的一致性研究[D]. 广西师范大学,2019.
[5] Porter.A,Smithson.J,BlankR&Zcidner.T.Alignment as a Teacher Variable [J]. App licd M easurement in Education,2007(20):27-52.
[6] Fulmer Gavin W. Estimating Critical Values for Strength of Alignment Among Curriculum,Assessments,and Instruction[J]. Journal of Educational and Behavioral Statistics,2011,36(03).
[7] 喻平. 數学核心素养评价的一个框架[J]. 数学教育学报,2017,26(02):19-23+59.
[8] 吴晓红. 核心素养视域下高中数学新教材习题与课程标准的一致性研究[D]. 广西师范大学学,2021.
