基于实验分析的逐差法教学
2023-05-30顾卓光
顾卓光


摘 要:基于实验分析进行逐差法教学,通过逐差法的根基、逐差法的生成、逐差法的提出、逐差法的活用四个环节的精心设计,让学生深刻理解“逐差法充分利用了测量数据,具有对数据取平均的效果”这一核心要义。
关键词:平均值;逐差法;位移差
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2023)5-0057-3
逐差法求加速度是高中物理运动学部分的必学内容。由于教材中没有安排专门的章节介绍逐差法,因此在什么时候以什么方式讲授逐差法,也就仁者见仁、智者见智。一般的做法是,在学完匀变速直线运动的基本规律后,以导出规律或推论的形式介绍逐差法,然后在实验数据的处理中运用逐差法计算加速度。这种从原理到应用的教学设计中规中矩、省时省力,但有所欠缺的就是学生对“逐差法充分利用了测量数据,具有对数据取平均的效果”这一核心要义体悟不深。在筆者讲评下面这道课本习题时,萌生了基于实验分析进行逐差法教学的想法,并付诸实践,教出了全新的感觉。课堂设计由逐差法的根基、逐差法的生成、逐差法的提出、逐差法的活用四个板块构成。
1 原题呈现
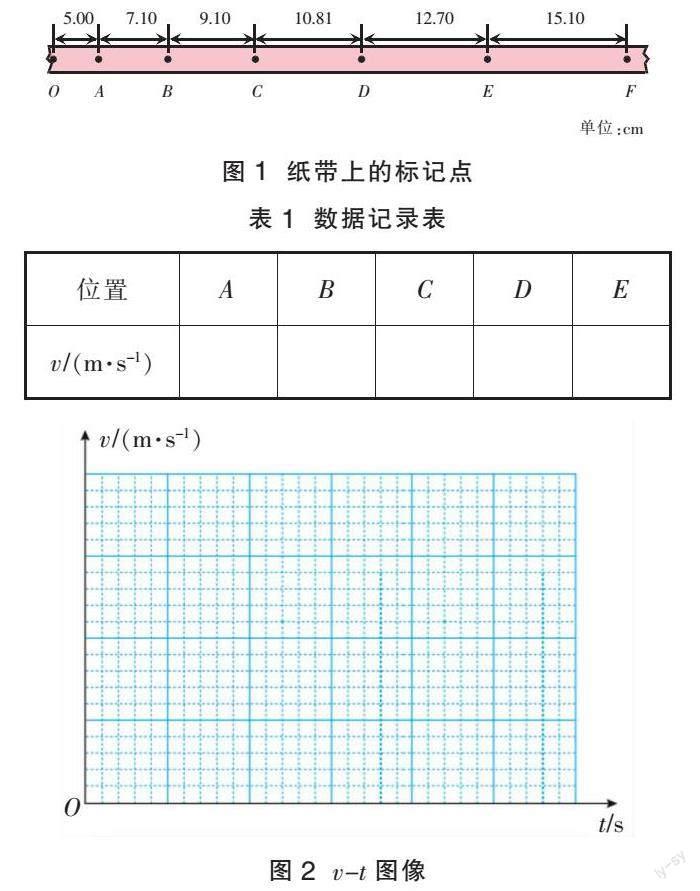
(人教版普通高中教科书物理必修第一册,54页题4) 某同学在“探究小车速度随时间变化的规律”实验中,选出了如图1所示的一条纸带(每两点间还有4个点没有画出来),纸带上方的数字为相邻两个计数点间的距离。打点计时器的电源频率为50 Hz。
(1)根据纸带上的数据,计算打下A,B,C,D,E点时小车的瞬时速度并填在表1中。
(2)在图2中画出小车的v-t图像,并根据v-t图像判断小车是否做匀变速直线运动。如果是,求出该匀变速直线运动的加速度。
2 逐差法的根基
提出问题 前述这道题,我们依据v-t图像可判断出小车做匀变速直线运动,并由图像的斜率求出其加速度a=1.94 m/s2(1.90 m/s2~1.99 m/s2均可)。可否从加速度的定义出发,根据纸带上的数据计算小车加速度的大小呢?
这个结果与用v-t图像求出的加速度吻合得很好。这种计算加速度的方法应当是最优方法,与通过v-t图像的斜率求加速度有殊途同归、异曲同工之妙。
【设计意图】 多次测量取平均值,是减小偶然误差的常用方法,但在这个实验中碰到了新问题。通常的做法造成了数据丢失,肯定不可取。为保全数据,做了两次修正,可结果还是偏差很大。直至第三种修正方案才使测量值落在了实验误差允许的范围内。至此,逐差法呼之欲出。此番设计,一波三折,能让学生充分经历知识发生的过程,充分感受求知过程中“不愤不启,不悱不发”的心路历程。
4 逐差法的提出
方法提炼 平均值法是减小偶然误差的基本方法之一。针对如何处理纸带上的多段数据得出加速度,我们一步步摸索出了一种行之有效的方法。回到前面的实验题中,把这种方法再进行提炼。
该式表明,可以把纸带上的6段数据分成两大段,用后一段的位移之和减去前一段的位移之和,除以这两大段对应的时间间隔3T的二次方,即得所测加速度。其实质与位移差公式Δx=aT2一脉相承,可理解成放大了的位移差公式。
明确名称 今后,遇到根据纸带上的多段数据求加速度的问题,在不要求作v-t图像的情况下,就可参照上述方法计算。通常把这种方法叫作逐差法。
【设计意图】 如果说“逐差法的生成”是“由薄到厚”的过程,那么“逐差法的提出”则是“由厚到薄”的过程,用最简洁的语言表述逐差法的思想方法,是教学进行到这里的应然结果。为此,笔者结合文首的课本习题,给出了逐差法的公式表达,并辅以物理释义,以利学生理解、记忆、运用。
5 逐差法的活用
提出问题 这道实验题,纸带上的逐段数据正好是偶数段,如果给出的逐段数据是奇数段,如只给出x1,x2,x3,x4,x5,如何用逐差法计算加速度呢?
【设计意图】 事情有时是复杂的,逐差法也不例外。如何用逐差法处理奇数段问题,有必要向学生介绍一下思路和方法。这样,逐差法的教学就相对完整了。
基于实验分析的逐差法教学,虽然有些费时费力,但有助于学生深刻理解“逐差法充分利用了测量数据,具有对数据取平均的效果”这一核心要义。通过探究活动,建立概念、发现规律、形成观念、发展思维、学会方法、养成态度,核心素养理念下物理教学的特征在这堂课上体现得淋漓尽致。
(栏目编辑 蒋小平)