Constraints on Dark Energy from the CSST Galaxy Clusters

Yufei Zhang, Mingjing Chen, Zhonglue Wen, and Wenjuan Fang

1 CAS Key Laboratory for Research in Galaxies and Cosmology, Department of Astronomy, University of Science and Technology of China, Hefei 230026,China; wjfang@ustc.edu.cn

2 School of Astronomy and Space Science, University of Science and Technology of China, Hefei 230026, China

3 National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China; zhonglue@nao.cas.cn

4 CAS Key Laboratory of FAST, NAOC, Chinese Academy of Sciences, Beijing 100101, China

Abstract We study the potential of the galaxy cluster sample expected from the Chinese Space Station Telescope (CSST)survey to constrain dark energy properties.By modeling the distribution of observed cluster mass for a given true mass to be log-normal and adopting a selection threshold in the observed mass M200m ≥0.836×1014 h-1 M⊙,we find about 4.1×105 clusters in the redshift range 0 ≤z ≤1.5 can be detected by the CSST.We construct the Fisher matrix for the cluster number counts from CSST, and forecast constraints on dark energy parameters for models with constant(w0CDM)and time dependent(w0waCDM)equation of state.In the self-calibration scheme,the dark energy equation of state parameter w0 of the w0CDM model can be constrained to Δw0=0.036.If wa is added as a free parameter,we obtain Δw0=0.077 and Δwa=0.39 for the w0waCDM model,with a Figure of Merit for(w0,wa) of 68.99.Should we have perfect knowledge of the observable-mass scaling relation (“known SR”scheme),we would obtain Δw0=0.012 for the w0CDM model, and Δw0=0.062 and Δwa=0.24 for the w0waCDM model.The dark energy Figure of Merit of (w0, wa) increases to 343.25.This indicates again the importance of calibrating the observable-mass scaling relation for optically selected galaxy clusters.By extending the maximum redshift of the clusters from zm ax ～ 1.5to zm ax ～ 2,the dark energy Figure of Merit for(w0,wa)increases to 89.72(self-calibration scheme) and 610.97 (“known SR”scheme), improved by a factor of ～1.30 and ～1.78,respectively.We find that the impact of clusters’redshift uncertainty on the dark energy constraints is negligible as long as the redshift error of clusters is smaller than 0.01, achievable by CSST.We also find that the bias in logarithm mass must be calibrated to be 0.30 or better to avoid significant dark energy parameter bias.

Key words: (cosmology:) dark energy – galaxies: clusters: general – (cosmology:) cosmological parameters

1.Introduction

The concordance Λ cold dark matter (ΛCDM) model has proven to provide an accurate description of the universe(Planck Collaboration et al.2020).Nevertheless, the main constituents in the model, namely dark energy (DE) and dark matter (DM), still need explanations from fundamental physics.Questions such as whether DE is indeed the cosmological constant (Zel’dovich 1967, 1968), or whether modified gravity theory rather than DE and DM actually explains the observable universe (Hu & Sawicki 2007;Capozziello & de Laurentis 2011), remain unsolved.These questions provide motivations to look for alternatives to the ΛCDM model.Future high precision cosmological surveys will constrain various such models and clarify many unsolved fundamental questions.

DE, unlike other known forms of matter or energy, is a component postulated to cause the late time accelerated expansion of the universe with a negative pressure (Riess et al.1998;Perlmutter et al.1999).Multiple observational evidences point to the existence of DE.However, to date there are no compelling theoretical explanations yet.The most popular model of DE is the cosmological constant whose equation of state(EoS)is-1.There are other models in which the EoS of DE is not -1 or even not constant but time-dependent, for example, quintessence (Ratra &Peebles 1988),phantom(Caldwell 2002)and quintom(Feng et al.2005).The accelerated expansion of the universe may even imply that gravity should be described by a modified theory of gravity, rather than the standard theory of General Relativity(Heisenberg 2019).Different models of DE leave different signatures in the expansion rate of the universe and the growth rate of structure.Thus surveys that observe the universe’s supernovae, galaxies, galaxy clusters, etc., can potentially reveal the nature of DE (e.g., Zhao et al.2017).

In the hierarchical structure formation scenario,small density fluctuations generated in the primordial universe act as the seeds for the formation of the universe’s structure.Overdensities in the early universe grow through gravitational instability and hierarchically form larger and larger structures(Peebles 1980;Colberg et al.1999).Galaxy clusters are the largest virialized objects in the universe.Searches for galaxy clustershave been carried out for decades from multiwavelength data,such as the millimeter wave bands (e.g., de Haan et al.2016;Planck Collaboration et al.2016; Bleem et al.2020), the optical wave bands(e.g.,Wen et al.2009;Rozo et al.2010;Oguri et al.2018;Costanzi et al.2019;DES Collaboration et al.2020;Wen&Han 2021)and the X-ray wave bands(e.g.,Vikhlinin et al.2009;Clerc et al.2012; Rapetti et al.2013; Böhringer et al.2017;Pacaud et al.2018).The abundance and spatial distribution of galaxy clusters are sensitive to the universe’s expansion and growth rate and hence underlying cosmological model (Allen et al.2011; Kravtsov & Borgani 2012; Weinberg et al.2013).Clusters have been used to constrain the matter density parameter Ωmand the present day root mean square (rms) of linear density fluctuations within a sphere of radius 8 h-1Mpc, σ8(e.g., Rozo et al.2007, 2010; Rapetti et al.2013; de Haan et al.2016;Costanzi et al.2019; DES Collaboration et al.2020, 2021).Moreover,since massive neutrinos suppress matter fluctuations on small scales,this impact on the growth of structure manifests itself in cluster observables, which can be used to constrain neutrino mass (Costanzi et al.2013; Mantz et al.2015; Planck Collaboration et al.2016).Clusters have also been demonstrated to provide tight constraints on DE from their abundance (Mantz et al.2010; Rozo et al.2010; Mantz et al.2015; de Haan et al.2016), spatial clustering (Schuecker et al.2003; Abbott et al.2019; DES Collaboration et al.2021) and gas mass fractions(Allen et al.2008; Mantz et al.2014, 2021).However, the precision on cosmological parameters derived from cluster observables is affected by both theoretical and observational systematic uncertainties.

Table 1 Key Parameters of the CSST Photometric Imaging Survey and Spectroscopic Survey (Zhan 2021)

Forthcoming large surveys, for example the Vera Rubin Observatory (LSST Science Collaboration et al.2009;Ivezić 2019), Euclid space mission (Laureijs et al.2011) and Chinese Space Station Telescope(CSST)(Zhan 2011;Cao et al.2018; Gong et al.2019), have the potential to find a large number of clusters.Specifically, the CSST is a 2 m space telescope planned to be launched in the early 2020s.It will operate in the same orbit as the China Manned Space Station.The CSST aims at surveying 17,500 deg2of sky area over 10 yr of operation.Both photometric imaging and slitless grating spectroscopic observations will be conducted.With the unique combination of a large field of view (～1 deg2), high-spatial resolution(～0 15),faint magnitude limits and wide wavelength coverage, CSST has great potential to investigate many fundamental problems, such as properties of DE and DM,validity of General Relativity on cosmic scales,etc.(Zhan 2011).In particular,CSST will detect a large number of clusters through photometric imaging, spectroscopic observation and weak gravitational lensing, thanks to its large sky coverage and wide redshift range, which will be valuable for cosmological studies.

We list the key parameters of the CSST survey in Table 1.There are seven photometric and three spectroscopic bands from near-ultraviolet (near-UV) to near-infrared (near-IR), namely,NUV, u, g, r, i, z and y bands for the photometric survey, and GU, GV and GI bands for the spectroscopic survey.The CSST photometric survey can reach a 5σ magnitude limit of ～26 AB mag for point sources, while for spectroscopic survey, the magnitude limit can reach ～23 AB mag.The 4000 Å break,Lyman break and 1.6 μm bump are distinct features to determine photometric redshifts of galaxies.The photometric redshifts of galaxies can be well determined up to the redshift of z ～1.4,at which the 4000 Å break moves to the y band.At higher redshifts,the Lyman break begins to move into the CSST filters.Considering the relatively shallow survey depth in the NUV band, it is expected that the photometric redshifts have a larger bias and uncertainty at 1.4 ＜z ＜2.5 (even with the presence of NUV, the photometric redshift is not much improved in the redshift range,Rafelski et al.2015).They can be improved with the help of other surveys whose band coverage extends to midinfrared and near-IR bands, such as Wide-field Infrared Survey Explorer (WISE, Wright et al.2010) and Euclid (Laureijs et al.2011; Sartoris et al.2016).

In this paper, we explore the power of the CSST cluster sample in constraining DE parameters.We consider two DE models.The first one is the model in which the EoS parameter w of DE is allowed to deviate from -1 in a time independent fashion (w0CDM).In the second model, the EoS of DE is varying with time (w0waCDM), with the phenomenological parameterization w(a)=w0+(1-a)wa, where a is the scale factor of the universe (Chevallier & Polarski 2001; Linder &Jenkins 2003).We estimate the abundance of galaxy clusters expected from CSST and forecast its constraints on cosmological parameters by using the Fisher matrix technique.To calculate galaxy cluster number counts, we first compute the halo mass function by adopting the fitting function from Tinker et al.(2008).Then the number counts in an observed mass bin can be computed once the probability to assign an observed mass to a cluster’s true mass is given.Finally, we can evaluate cluster number counts as a function of the estimated mass and redshift.By combining the number of clusters in bins of estimated mass and redshift, we construct the Fisher matrix and then derive the forecasted constraints on cosmological parameters.

This paper is organized as follows.In Section 2, we detail our estimation for the galaxy cluster abundance expected for the CSST, and present the Fisher matrix we use to forecast parameter constraints.In Section 3, we give our results and discuss the effects of several systematics.Finally,we conclude in Section 4.

2.Calculational Methods

2.1.Mass Estimation for CSST Clusters

Cluster mass is of fundamental importance for studies on cluster properties and cluster cosmology.Regardless of how clusters are detected at different wavelengths,the main concern is that halo mass is not directly observable,so we have to employ a suitable observable quantity that scales with mass.In the case of optical surveys, a commonly used mass proxy is the optical richness λ,which corresponds to the count or total luminosity of member galaxies above some luminosity threshold in a given cluster(Rozo et al.2009;Wen et al.2012).The calibration of the relation between richness and halo mass for optically selected clusters can be performed through cluster number counts,clustering and stacked weak-lensing measurements (e.g., Murata et al.2018; Costanzi et al.2019; Murata et al.2019; Chiu et al.2020a,2020b;DES Collaboration et al.2020;Wen&Han 2021).

For the CSST survey,each galaxy cluster is identified with an optical richness estimated.Mean mass of clusters can be measured directly through weak lensing for a sample of stacked clusters within a given richness and redshift bin.Then, one can get an“accurate”richness-mass scaling relation and its evolution with redshift.In the regime where the weak lensing method is not applicable, e.g., very high redshifts, cluster mass can be estimated according to the derived richness-mass relation.

2.2.Calculation for Cosmological Constraints

A fundamental quantity for cluster cosmology is the halo mass function, which is defined as the differential number density of halos.In this paper,we adopt the halo mass function obtained by Tinker et al.(2008)

where f(σ) is the fitting function given by Equation (3) in Tinker et al.(2008), ρmis the present matter density of the universe and σ is the rms of linear matter fluctuation within a sphere of radius R that contains mass M given mean density of

In the above expression, P(zob|z) is the probability distribution function to assign a galaxy cluster at true redshift z to the observed photometric redshift zob, which we model as a Gaussian distribution with expectation value z and scatter σz.

The comoving space number density of clusters〈n|Mob,z〉is related to halo mass function by

where P(Mob|M, z) is the probability distribution function to assign a galaxy cluster with true mass M and at true redshift z to the observed mass Mob.

The survey volume element dV/(dzdΩ) is given by

where H(z) is the Hubble parameter and χ(z) is the comoving radial distance to redshift z.

The key ingredient in our analysis is the probability distribution function of the observed mass for halos with a given true mass M and redshift z, P(Mob|M, z).Following Sartoris et al.(2016), we assume a log-normal distribution function, namely

HerelnMbiasandσlnMare the bias and scatter of mass estimation in logarithm space, respectively.Following Sartoris et al.(2016), we parameterize the bias as

We assume the following parameterization for the variance oflnM

Here the first term comes from the fact that cluster mass commonly scales with optical richness.The variance of lnλis composed of a constant intrinsic scatter Dλand a Poisson-like term (Costanzi et al.2021)

where the term 1/〈λ〉is a function of cluster mass and redshift.The fiducial values ofσlnλand B can be obtained from the scaling relation fitted by Costanzi et al.(2021)

Here,A is the normalization,B is the slope with respect to halo mass and Bzdescribes the evolution with redshift.The constants Mpivotand zpivotare pivot halo mass and redshift respectively.We emphasize that Equation (10) is not used for cluster mass estimation, but for the scatter of mass estimation.

The second term κ(1+z)2in Equation (8) characterizes the projection effects that depend on redshift.The reason for the chosen form of the projection effects is as follows.The photometric redshift error of galaxies usually increases with redshift.In the algorithms of cluster identification,the width of color cut or photometric redshift slice increases with redshift for both the color-based and photometric redshift-based methods (Wen et al.2009; Rykoff et al.2014).As is wellknown, the dispersion of photometric redshift generally increases with redshift in the form of 1+z (Cao et al.2018).From the perspective of identifying galaxy clusters,in order to obtain the majority of member galaxies, the width of the photometric redshift slice used to find galaxy clusters also increases as 1+z, resulting in the corresponding increase of field galaxies projecting into cluster regions as member galaxies.In Wen et al.(2009), the authors adopted a photometric redshift slice of z±0.04(1+z) for the Sloan Digital Sky Survey(SDSS)clusters and found a contamination rate of ～20%for member galaxies due to the projection effect.The CSST will have a more accurate photometric redshift than the SDSS (Cao et al.2018), which will enable us to set a narrower photometric redshift slice for selecting member galaxies of clusters.In addition, the slitless spectroscopic survey provides accurate redshifts for bright galaxies.It is possible to have a contamination rate of about 10% at low redshift for massive clusters.Therefore,we assume κ=0.12as a fiducial choice.

We forecast the constraints on cosmological parameters using the Fisher matrix technique, which is based on a Gaussian approximation of the likelihood function around the maximum (Tegmark et al.1997).The Fisher matrix is defined as

where pα, pβrepresent model parameters,L is the likelihood function and angle brackets represent ensemble average.The marginalized 1σ constraint on parameter pαcan then be obtained by

In our analysis we choose the galaxy cluster number counts Nm,ias observable.The likelihood of Nm,ican be modeled as a Poisson distribution with the expectation valueN¯m,i,

Thus the Fisher matrix for cluster number counts is

Here, the sums over m and i run over mass and redshift bins,respectively.

We adopt the Figure of Merit(FoM,Albrecht et al.2006)for DE to quantify the information gains from given probes and experiments, which is inversely proportional to the area encompassed by an ellipse representing the 68.3 percent confidence level

where Cov(w0, wa) is the marginalized covariance matrix for the DE EoS parameters w0and wa.

In our Fisher matrix analysis, both cosmological parameters and the parameters modeling bias and scatter in the scaling relation between the observed and true cluster masses are treated as free parameters, and are constrained simultaneously.We assume a flat universe and choose our cosmological parameter set as: {h, Ωbh2, Ωch2, σ8, ns, w0, wa}.Fiducial values of these parameters are listed in Table 2, which are the best-fit values from Planck 2018 results (Planck Collaboration et al.2020).We marginalize over the set of scaling relation parameters {BM,0, α, A, B, Bz, Dλ, κ} given above, referred to as nuisance parameters henceforth, whose fiducial values are listed in Table 2.The values of BM,0and α are chosen according to Sartoris et al.(2016),while the values of A,B,Bzand Dλare the best-fit values obtained in Costanzi et al.(2021).The pivot values for halo mass and redshift(Mpivotand zpivot)inEquation (10) are taken to be 3×1014h-1M⊙and 0.45,respectively, following Costanzi et al.(2021).

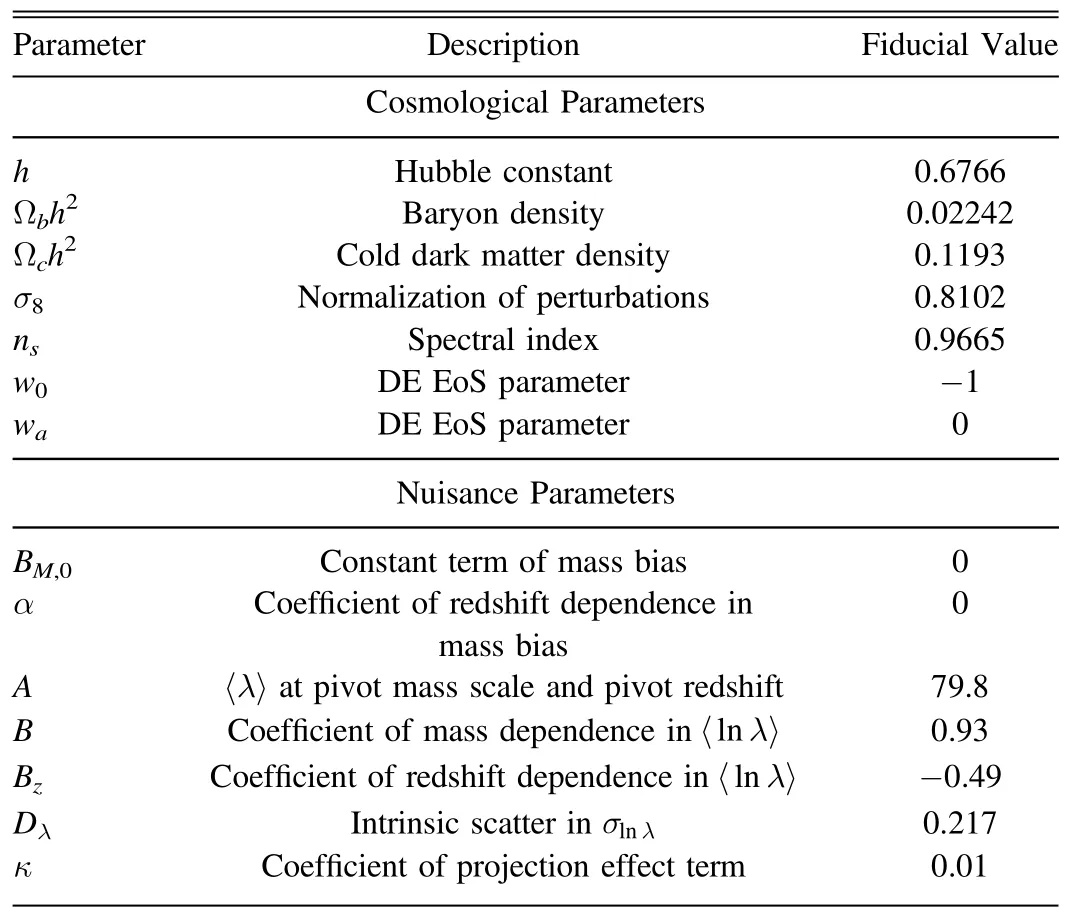
Table 2 The Fiducial Values of Cosmological Parameters (Upper Section) and Nuisance Parameters (Lower Section) Adopted in this Work

3.Results and Discussions

In this section, we present the main results of this paper:constraints on the DE EoS parameters from galaxy cluster number counts of CSST, forecasted with the Fisher matrix formalism.Several systematics are also discussed simultaneously.We consider DE models with constant (w0CDM) and time dependent(w0waCDM)DE EoS.We assume that CSST is capable of detecting clusters up to z ～1.5 by either the redshiftbased method (e.g., Wen & Han 2021; Yang et al.2021) or color-based method (e.g., Rykoff et al.2014).We divide the CSST cluster sample into bins both in redshift and halo mass.For redshift, we consider equal-sized bins of width Δz=0.05 in the range 0 ≤z ≤1.5.For observed halo mass, we take equal-sized logarithmic bins of width Δln (MobM⊙) =0.2.We ignore the covariance between different redshift and mass bins.We assume 17,500 deg2sky coverage for the CSST optical wide survey.Most CSST galaxies will have photometric redshift uncertainties of about 0.02 (Gong et al.2019).Moreover, CSST will perform a slitless grating spectroscopic survey for bright sources in addition to a photometric imaging survey.Taking into account that clusters have multiple bright member galaxies whose spectroscopic redshifts are probably available from CSST slitless or existing spectroscopic surveys,we expect CSST clusters will have an accurate redshift.In this work, we assume CSST clusters’redshift uncertainty to be σz/(1+z)=0.001.

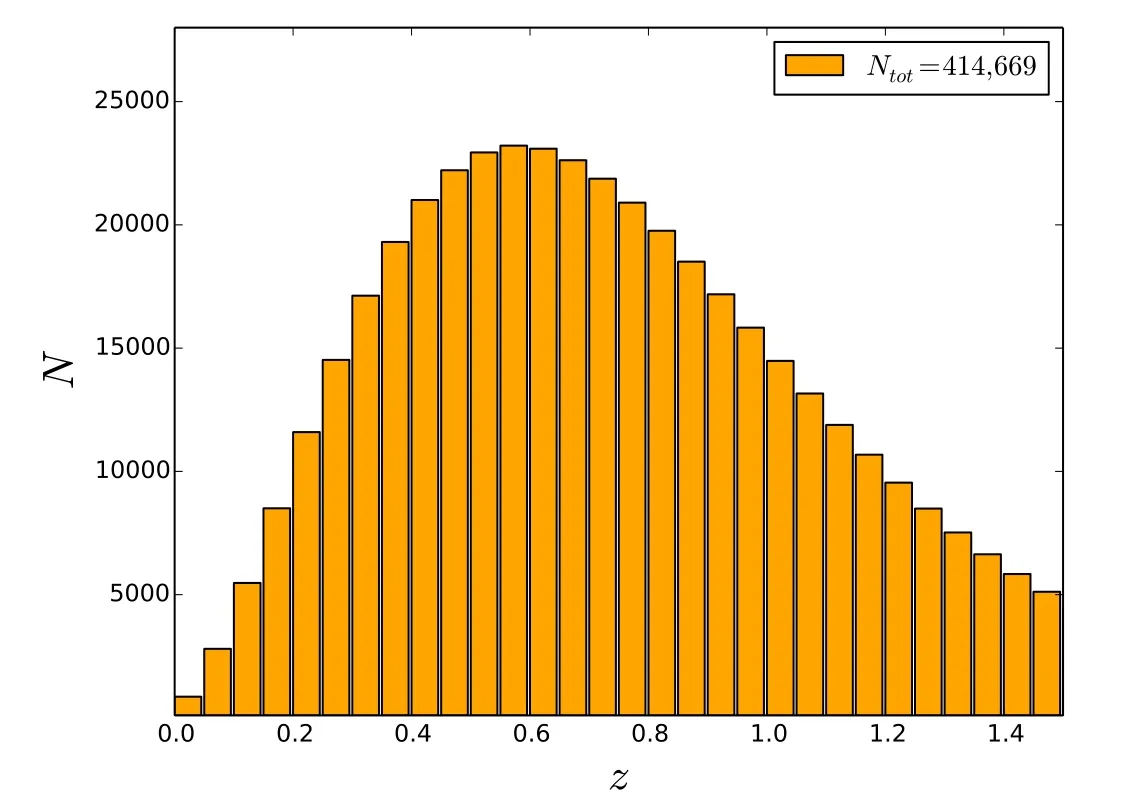
Figure 1.Redshift distribution of galaxy clusters expected for CSST; mass threshold is set to M200m ≥0.836×1014 h-1 M⊙(M500c ≥0.7×1014 M⊙).

3.1.Mass Limit and Number Counts

The lower limit of cluster mass corresponds to a given detection threshold in the observed quantity.The limit is adopted to ensure that the cluster sample obtained has a high completeness and also a high purity.According to the analysis based on mock galaxy redshift survey data (Yang et al.2021),we adopt a lower mass limit of M200m≥0.836×1014h-1M⊙for the CSST cluster sample in order to get a completeness of≥90% and a purity of ≥90%.This mass limit roughly corresponds to an equivalent mass limit of M500c≥0.7×1014M⊙(Wen & Han 2021).

In Figure 1,we plot the expected number of clusters that can be detected by CSST as a function of redshift, obtained by adopting the observed halo mass limit M200m≥0.836×1014h-1M⊙and assuming the fiducial values of cosmological and nuisance parameters.We find that CSST can detect～414,669 clusters in total in the redshift range 0 ≤z ≤1.5,with a peak at z ～0.6, and there are ～103,069 clusters at z ≥1.0.These high redshift clusters are sensitive to the growth rate of perturbations and DE properties.A catalog of uniformly selected high-redshift clusters will be ideal to study structure growth and the underlying cosmological model.

3.2.Constraints from Cluster Number Counts

Since besides cosmological parameters, there are also nuisance parameters which model bias and scatter in the scaling relation between the observed and true cluster masses,we forecast constraints on DE EoS parameters from galaxy cluster number counts of CSST with two schemes: a selfcalibration scheme in which we take both cosmological parameters and nuisance parameters as parameter entries for the Fisher matrix(Majumdar&Mohr 2004),and the ideal caseNote.The column labeled“Self-calibration”corresponds to the self-calibration scheme without any priors on the nuisance parameters.The column “Known SR”refers to the ideal case in which the nuisance parameters are perfectly known.Constraints shown are the marginalized 1σ errors.The DE FoM is presented in the last row.in which the nuisance parameters are fixed, which means that scaling relations are perfectly known in advance(referred to as the “known SR”scheme in the following).

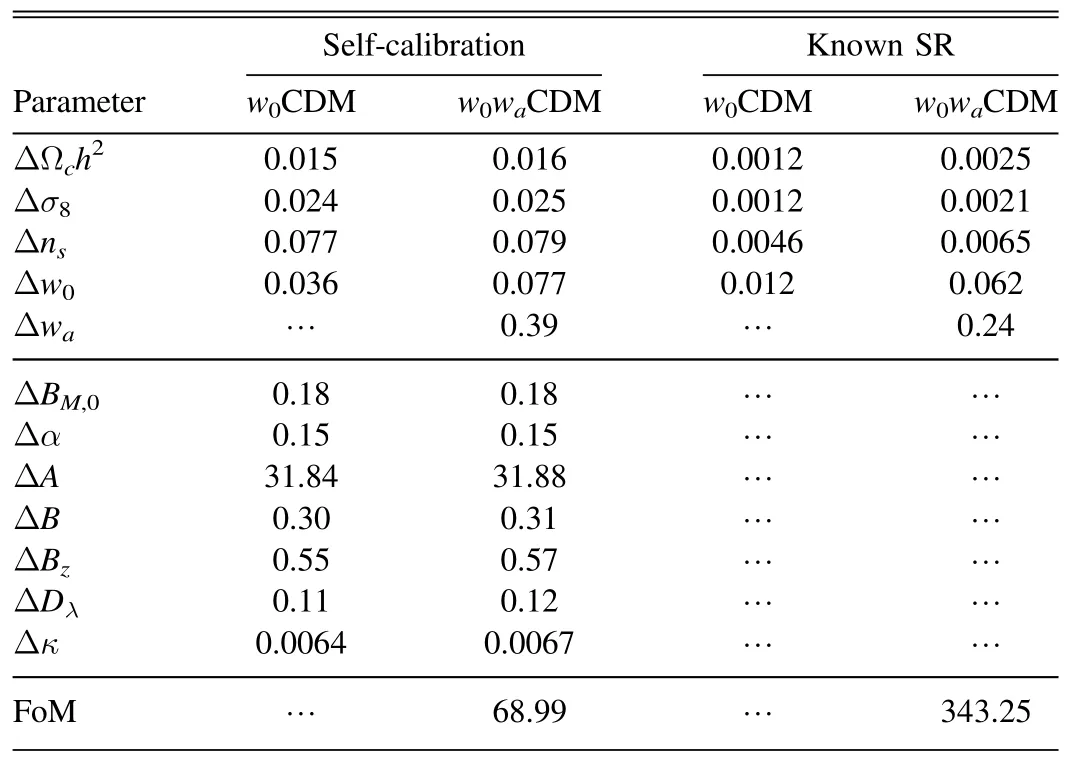
Table 3 Constraints on the Cosmological Parameters and Nuisance Parameters from the Number Counts of CSST Galaxy Clusters

It is challenging to constrain the cosmological parameters and nuisance parameters simultaneously by using the number counts of galaxy clusters alone.In the following analysis we include the Gaussian priors on the Hubble parameter and the cosmic baryon density from the Planck collaboration (Planck Collaboration et al.2020) to help break parameter degeneracies.

The constraints on the cosmological parameters from CSST galaxy cluster number counts are presented in Table 3 for the two schemes.In the self-calibration scheme, the DE EoS parameters can be constrained to Δw0=0.036 for the w0CDM model, and Δw0=0.077 and Δwa=0.39 for the w0waCDM model,corresponding to a DE FoM for(w0,wa)of 68.99.In the“known SR”scheme,cluster mass has no bias and the scatter of cluster mass is known.The constraint on w0is as good as Δw0=0.012 for the w0CDM model, an improvement by a factor of ～3 compared to the results of the self-calibration scheme, while for the w0waCDM model, we obtain Δw0=0.062 and Δwa=0.24.The DE FoM is as high as 343.25, an improvement by a factor of ～5 compared to the results of the self-calibration scheme.It is apparent that knowledge of the observable-mass scaling relation is essential to get tighter cosmological parameter constraints.The analysis here highlights the importance of the calibration of the observable-mass scaling relation for optically selected galaxy clusters in order to obtain tight DE constraints.We postpone a comparison with other optical cluster surveys to Section 3.6.

It is known that besides DE parameters, clusters can also place tight constraints on DM related parameters.The 1σ uncertainties on Ωch2and σ8are about 1%～2%with the selfcalibration scheme, while 0.1%–0.2% with the “known SR”scheme.The improvements from better knowledge of the observable-mass scaling relation are more pronounced for constraints on Ωch2and σ8than for w0and wa.Comparing the constraints from the self-calibration scheme and those from the“known SR”scheme, the constraint on Ωch2is improved by a factor of 12.5 for the w0CDM model and a factor of 6.4 for the w0waCDM model, while the constraint on σ8is improved by a factor of 20 for the w0CDM model and a factor of 12 for the w0waCDM model.Thus better calibration of the observablemass scaling relation is more helpful to tighten the constraints on DM related parameters than DE parameters.We show contours of constraints(1σ)on cosmological parameters for the w0waCDM model in the Appendix.

We point out that in this analysis we assume a possible configuration of CSST.In the following we analyze the impact of two key parameters on our derived constraints, i.e., the maximum redshift and the clusters’redshift uncertainty.We also compute the requirement for the calibration of bias in cluster mass.

3.3.Increasing zmax of CSST Clusters

In the above analysis for the CSST clusters,we have adopted a maximum redshift ofzmax～ 1.5.Higher redshift is potentially achievable with an improved cluster selection algorithm, better data quality or joint analysis with the Euclid survey by the European Space Agency (Laureijs et al.2011),which can detect clusters up to redshift as high as ～2 thanks to the use of near-IR bands (Sartoris et al.2016).

In this section, we study the impact of including higher redshift clusters in our forecast by increasing the maximum redshift of the CSST cluster sample.Specifically, when we extend zmaxto ～2, we find that 28,492 clusters between 1.5 ≾z ≾2 can be additionally detected, ～7% more than before.The DE constraints obtained by extending the maximum redshift of the clusters tozmax～ 2are presented in Table 4.By extending the maximum redshift of the survey fromzmax～ 1.5tozmax～ 2, the DE constraints are tightened for both the w0CDM model and w0waCDM model.The constraint on w0for the w0CDM model is improved by a factor of ～1.06 for the self-calibration scheme,and a factor of ～1.28 for the “known SR”scheme.While for the w0waCDM model,the DE FoM is improved by a factor of ～1.30 for the selfcalibration scheme, and a factor of ～1.78 for the “known SR”scheme.As can be seen,even moderate detection of clusters at high redshift can tighten the constraints by an appreciable amount.The reason is that the behavior of DE deviates morefrom the ΛCDM model in the earlier universe.Therefore if the survey can cover a large redshift range, a comparison of the behavior of DE at different redshifts helps to break parameter degeneracies.

Table 4 Constraints on DE EoS Parameters by Extending the Maximum Redshift of the CSST Clusters tozm ax ～2

In Figure 2,we show how the FoM for DE parameters in the w0waCDM model changes as the maximum redshift of the CSST clusters increases continuously.For both the self-calibration and“known SR”schemes,the DE FoM increases steadily with zmax.Thus it is important to search for clusters at high redshift for stringent constraints on DE properties.It is also interesting to note that the FoM obtained from the “known SR”scheme increases more rapidly than that from the self-calibration scheme.Thus high redshift clusters are more helpful to constrain DE if clusters have a well calibrated scaling relation.

3.4.The Impact of Redshift Uncertainty

The constraints above are obtained by assuming a somewhat optimistic redshift uncertainty of σz/(1+z)=0.001, which we expect to be achievable under the assumption that spectroscopic redshifts are available for all clusters from CSST.In this section,we study the impact of less accurate redshifts for clusters on the cosmological constraints by assuming the CSST clusters have redshift accuracy of σz/(1+z)=0.03, 0.02 and 0.01.In Figures 3 and 4, we show how the constraints on DE EoS parameters change with respect to clusters’redshift accuracy.The error ellipses in Figure 3 are obtained with the selfcalibration scheme, while those in Figure 4 are obtained by the“known SR”scheme.In both figures, the DE constraints get tighter as CSST clusters’redshift uncertainty becomes smaller.However, the improvement in DE constraints is tiny from σz/(1+z)=0.01 to σz/(1+z)=0.001.For the self-calibration scheme, the DE FoM improves from 68.44 to 68.99, while for the “known SR”scheme, the FoM improves from 340.09 to 343.25.In both cases, the improvement is less than 1 per cent.We conclude that the impact of CSST clusters’redshift uncertainty is negligible as long as the rms of redshift uncertainties is better than 0.01.According to Wen & Han(2022),the redshift uncertainty of DES clusters is about 0.013 at redshifts z ≤0.9.Since CSST has two more wave bands than DES, we expect σz/(1+z)=0.01 is achievable by the CSST optical survey.We also find that if the clusters’redshift error degrades further to 0.03,FoM decreases only by a small amount of ～9%for both the self-calibration and “known SR”schemes.

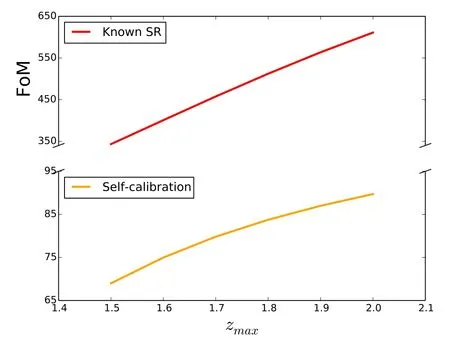
Figure 2.The DE FoM as a function of the maximum redshift zmax of the CSST clusters.Orange line stands for constraints obtained by the selfcalibration scheme.Red line represents constraints obtained by the “known SR”scheme.

Figure 3.Impact on DE constraints from the CSST clusters’redshift uncertainty.The contours are obtained with the self-calibration scheme.Orange, blue, black and red lines are for σz/(1+z) equating 0.03, 0.02, 0.01 and 0.001, respectively.

3.5.Mass Bias Calibration

In our analysis,the fiducial value of bias in observed mass is set to zero.However,if the observed cluster mass is biased,the derived DE parameter constraints will also be biased.It is interesting to ask that given the statistical accuracy achievable by the CSST clusters, what is the requirement for the calibration of bias in cluster mass.

Figure 4.Impact on the DE constraints from the CSST clusters’redshift uncertainty.The contours are obtained with the “known SR”scheme.Orange,blue, black and red lines are for σz/(1+z) equating to 0.03, 0.02, 0.01 and 0.001, respectively.

Consider data vectorD={Dα} with covariance matrix C.The data bias ΔD induces bias in the ith parameter pias(Bernstein & Huterer 2010)

The bias calibration requirement is set by requiring the induced parameter bias to be smaller than the expected statistical variation in the cosmological parameters.The likelihood of the bias for a subset of interested parameters ΔpAis determined by Bernstein & Huterer (2010)

3.6.Comparison with Other Optical Cluster Surveys

In this section,we make a comparison between our results of CSST and those of other optical cluster surveys,such as LSST and Euclid.First,we compare our results for the CSST clusters to those of LSST clusters by Fang&Haiman(2007)utilizing a shear-selected cluster sample.The halo mass definition adopted by Fang & Haiman (2007) is based on identification of DM halos as spherical regions with a mean overdensity of 180 with respect to the background matter density at the time of identification.With a sky coverage of 18,000 deg2,they found that LSST can detect 276,794 clusters in the redshift range 0.1 ≤z ≤1.4,above the limiting halo mass of ～(0.6–4)×1014M⊙.This number count is less than our result, since Fang &Haiman (2007) do not take into account uncertainties in the observable-mass scaling relation.Using cluster number counts alone, the forecasted FoM of DE EoS parameters (w0, wa) is 14.1,weaker than our result.This is due to less cluster number count obtained by Fang & Haiman (2007), and the WMAP priors adopted by them are much weaker than the Planck priors we adopt.

We also compare our results for the CSST to those of Euclid by Sartoris et al.(2016).The detection threshold of Euclid clusters is chosen such that N500,c/σfield, the ratio between the number of cluster galaxies N500,cand the rms of field galaxies σfield, is greater than 3 (or 5).The lowest limiting cluster mass for N500,c/σfield=3 is M200c～8×1013M⊙.With selection threshold N500,c/σfield=5,Euclid can detect ～2×105clusters up to redshift z ～2, with about ～4×104objects at z ≥1.By lowering the detection threshold down to N500,c/σfield=3, the total number of clusters rises up to ～2×106, with ～4×105objects at z ≥1.Our total number of clusters is between their estimated results for these two cases.Using cluster number counts alone, Euclid obtained DE FoM of ～30 for N500,c/σfield≥3 in the self-calibration scheme.Though the abundance of Euclid clusters is greater than ours, the constraints we obtained are more competitive than theirs,since Sartoris et al.(2016) also include curvature parameter Ωkin their Fisher matrix analysis.We also note that the parameterization for the mass scatter in Sartoris et al.(2016) is different from ours.

Finally, we notice that during the preparation of this paper,another result on DE constraints forecasted using the CSST galaxy clusters appeared in Miao et al.(2022).The cluster redshift range adopted by them is the same as ours.However,the limiting mass of clusters adopted by them (M ≥1014h-1M⊙) is higher than ours, and they do not take into account uncertainties in the observable-mass scaling relation, resulting in less clusters (～170,000) than ours.They obtain the forecasted DE constraints of Δw0=0.13 and Δwa=0.46 using the CSST cluster number counts, which are worse than ours, due to their much lower number of clusters and the fact that no Planck priors on the Hubble parameter and the cosmic baryon density are adopted in their analysis.

4.Conclusions

In this paper, we perform a comprehensive analysis of the constraints on DE for both constant (w0CDM) and timedependent (w0waCDM) EoS expected from the CSST galaxy clusters.We make our forecast by adopting the Fisher matrix formalism tailored for measurements of cluster abundance.In the self-calibration scheme, we consider 14 parameters, seven of which characterize the cosmological model, while the remaining seven model bias and scatter in the scaling relation between the observed and true cluster masses for optically selected clusters.With the selection threshold in the observed halo mass of M200m≥0.836×1014h-1M⊙, 414,669 clusters in the redshift range 0 ≤z ≤1.5 can be detected by the CSST,whose distribution peaks at z ～0.6.There are 103,069 clusters at z ≥1.0.The DE can be constrained to Δw0=0.036 for the w0CDM model, and Δw0=0.077 and Δwa=0.39 for the w0waCDM model, with a FoM of 68.99.

The self-calibration procedure would largely benefit from the fixed scaling relation.By fixing the seven nuisance parameters in our analysis, we get much tighter cosmological parameter constraints.We find that for the w0CDM model, the constraint on w0is as good as Δw0=0.012, an improvement by a factor of ～3 compared to the self-calibration scheme.If wais added as a free parameter, we obtain Δw0=0.062 and Δwa=0.24 for the w0waCDM model.The DE FoM for (w0,wa) is as high as 343.25,a great improvement by a factor of ～5 compared to the result of the self-calibration scheme.These results again highlight the importance of securing good knowledge of the observable-mass scaling relation.

We investigate the possibility of tightening the DE constraints further by increasing the redshift extension of the CSST clusters.We extend the maximum redshift of the CSST clusters out toz2 max～ and find that an extra 28,492 clusters between 1.5 ≾z ≾2 can be detected.The DE FoM for(w0,wa)increases to 89.72 and 610.97, for the self-calibration and“known SR”schemes, respectively, approximately improved by a factor of ～1.30 and ～1.78 from the results ofzmax～ 1.5.Thus,a small number of clusters at high redshift can tighten the cosmological constraints considerably, and high redshift clusters are more helpful to constrain DE with a better calibrated observable-mass scaling relation.

We find that the impact of the redshift uncertainty of clusters on the constraints of DE is negligible as long as the accuracy of redshift is better than 0.01, achievable by the current DES survey.If the clusters’redshift error degrades further to 0.03,FoM decreases only by a small amount of 9%.We also find that the logarithm mass bias must be calibrated to|BM,0|＜0.30 or better to avoid significant DE parameter bias.

In this work, we have focused on constraining DE parameters using cluster number counts alone.One can surely add in other cluster statistics to tighten the constraints with complementary information or better knowledge of systematics, for example the cluster power spectrum and the stacked lensing of clusters.On the other hand, various other fundamental problems can be investigated by using the CSST cluster sample,e.g.,neutrino mass,primordial non-Gaussianity or modified gravity.We plan to investigate these prospects in future study.

Acknowledgments

This work is supported by the National Key R&D Program of China grants Nos.2022YFF0503404 and 2021YFC2203102,by the National Natural Science Foundation of China (NSFC,Grant Nos.12173036, 11773024, 11653002, 11421303 and 12073036),by the China Manned Space Project grant No.CMSCSST-2021-B01, by the Fundamental Research Funds for Central Universities Grant Nos.WK3440000004 and WK3440000005, and by the CAS Interdisciplinary Innovation Team.

Appendix

Constraints on Cosmological Parameters

In this Appendix, for completeness and comparison with other work, we display the constraint contours for all cosmological parameters for the w0waCDM model, see Figure A1.We do not show the contours for the Hubble parameter or the cosmic baryon density since we have used the Planck priors on these two parameters.The constraints are obtained by the self-calibration scheme(blue)and“known SR”scheme (red), respectively, assumingzmax～ 1.5and clusters’redshift uncertainty of 0.001.It is clear from these contours that the constraining power from the CSST galaxy cluster survey will become much more powerful if the scaling relation sector is better understood.The improvements from better knowledge of the observable-mass scaling relation are more pronounced for constraints on other cosmological parameters(Ωch2,σ8and ns) than for w0and wa.The degeneracy directions of some cosmological parameters are different for the two schemes since the inclusion of observable-mass scaling relation parameters in the self-calibration scheme will alter the degeneracy directions of the cosmological parameters in the“known SR”scheme.

Figure A1.The contours of constraints (1σ) on cosmological parameters for the w0waCDM model obtained by the self-calibration scheme (blue) and “known SR”scheme (red), respectively.