3D Kinematics of Classical Cepheids According to GaiaEDR3 Catalog

V.V.Bobylev and A.T.Bajkova

Pulkovo Astronomical Observatory, St.-Petersburg 196140, Russia; vbobylev@gaoran.ru

Abstract The kinematics of about 2000 classical Cepheids of the Milky Way with data from Gaia EDR3 catalog has been studied.For some of these stars,there are line-of-sight velocities.On the basis of the nonlinear rotation model,the parameters of the rotation curve of the Galaxy were determined.The circular linear rotation velocity of the nearsolar neighborhood around the Galaxy center was V0=236±3 km s-1 for the assumed Sun’s galactocentric distance R0=8.1±0.1 kpc.Analysis of residual velocities of Cepheids based on the linear Ogorodnikov–Milne model showed the presence of the following significantly different from zero gradients: ∂U/∂x, ∂U/∂z, ∂V/∂x,∂V/∂z and ∂W/∂x, which behave differently depending on the selection radius.The most interesting is the gradient ∂W/∂x ～-0.5±0.1 km s-1 kpc-1(positive rotation of this star system around the Galactic axis y,Ωy)since the velocities W are free of Galactic rotation.Here we have an indirect influence of various effects leading to a perturbation of the vertical velocities of the Galactic disk stars.Based on a simpler model, a more accurate estimate of this rotation is obtained, Ωy=0.51±0.07 km s-1 kpc-1.

Key words: stars: distances – Galaxy: kinematics and dynamics – stars: variables: Cepheids

1.Introduction

Studying the rotation of the Galaxy is an important astronomical task.For this purpose, various Galactic objects are used—stars, star clusters, hydrogen clouds, star-forming regions, maser sources, etc.The local parameters of Galactic rotation are best studied in the region,where there are massive measurements of high-precision distances and kinematic characteristics of stars.At present, the radius of such a circumsolar region is 2–4 kpc.There are also other precise studies that measure rotation curves for heliocentric distance larger than 4 kpc(Xue et al.2008;Eilers et al.2019;Reid et al.2019; Ablimit et al.2020; Bobylev et al.2021; Gaia Collaboration et al.2022).

Cepheids make it possible to realize an independent distance scale due to the use of the period–luminosity relation (Leavitt 1908;Leavitt&Pickering 1912).Modern calibrations of this ratio allow estimating distances to Cepheids with errors less than 10% (Berdnikov et al.2000; Sandage & Tammann 2006;Skowron et al.2019a).Using such distances in combination with high-precision proper motions of about 220 classical Cepheids from The Hipparcos & Tycho Catalogues (1997), associated values were refined, for example, the Galaxy rotation parameters(Feast&Whitelock 1997;Mel’nik et al.2015),the spiral structure parameters (Mel’nik et al.1999; Bobylev & Bajkova 2012;Dambis et al.2015) and the distance to the center of the Galaxy(Chen et al.2018).According to data on older type II Cepheids,additional numerical values were refined including the parameters of the central bulge and other estimations of the distance to the center of the Galaxy as well (Majaess et al.2009; Bhardwaj et al.2017).

Recently, Skowron et al.(2019a) published an extensive catalog with new data on classical Cepheids.It contains more than 2200 stars,which are located in an area around the center of the Galaxy with a radius of about 24 kpc.According to these authors, the distances to these Cepheids are determined using the period–luminosity ratio with errors of 5%–10%.Thus, these Cepheids provide a unique opportunity to study the kinematic properties of the Galaxy in a very wide range of distances.Using the distances to these Cepheids, with the addition of their proper motions from the Gaia Data Release 2(DR2) catalog (Prusti et al.2016; Gaia Collaboration et al.2018), a number of works devoted to the analysis of the spatial distribution of Cepheids(Skowron et al.2019a,2019b;Bobylev & Bajkova 2021a), Galaxy kinematics (Mróz et al.2019;Ablimit et al.2020;Bobylev&Bajkova 2021b)and its spiral structure (for example, Bobylev et al.2021) have been performed.

In the Milky Way, there is a large-scale wave-like deformation of a thin disk–a Galactic warp.The positions of stars have characteristic deviations from the Galactic plane,which were established from an analysis of the distribution of various objects: neutral (Kalberla & Dedes 2008; Westerhout 1957) and ionized hydrogen (Russeil 2003; Cersosimo et al.2009), pulsars (Yusifov 2004), OB stars (Miyamoto &Zhu 1998; Drimmel et al.2000), red clump and old stars(López-Corredoira et al.2002; Momany et al.2006; Wang et al.2020), interstellar dust (Drimmel & Spergel 2001), or by Cepheids (Fernie 1968; Berdnikov 1987; Bobylev 2013a;Skowron et al.2019b).

Attempts to assess the kinematic properties of the warp and its influence on the motion of stars were undertaken in the works of a number of authors (for example, Miyamoto &Zhu 1998; Drimmel et al.2000; Bobylev 2013b; Poggio et al.2018, 2020; Wang et al.2020; Bobylev &Bajkova 2021b).In particular, Poggio et al.(2020), from an analysis of about 12 million giants from the Gaia DR2 catalog, estimated the warp precession rate as 10.86±0.03 (stat.)±3.20 (syst.) km s-1kpc-1in the direction of rotation of the Galaxy.According to Chrobáková & López-Corredoira (2021), the value found by Poggio et al.(2020) greatly exceeds theoretical predictions.Chrobáková & López-Corredoira (2021) showed that there is no need for precession if the change in the deformation amplitude depending on the age of the analyzed stellar population is taken into account.With this allowance, they,in particular, obtained an estimate of the deformation precession4-+46km s-1kpc-1.From the line-of-sight velocities and proper motions of classical Cepheids from the Gaia DR2 catalog, Bobylev & Bajkova (2021b) found residual rotation(as a manifestation of the warp effect)around the Galactic axis y with a velocity Ωy=0.54±0.15 km s-1kpc-1and positive rotation around the x axis with a velocity Ωx=0.33±0.10 km s-1kpc-1.

Currently, there are a number of papers devoted to discussing not only warp, but also other effects associated with vertical oscillations in the disk of the Galaxy(Antoja et al.2018; Bland-Hawthorn & Tepper-Garcıa 2021; Kumar et al.2022; Yang et al.2022).

The accuracy of parallaxes and proper motions of stars is important for solving a wide variety of kinematic problems.Currently, a version of the Gaia Early Data Release 3 (EDR3)catalog(Gaia Collaboration et al.2021)has appeared,in which,in comparison with the previous version, Gaia DR2 (Gaia Collaboration et al.2018), the trigonometric parallax values and proper motions are refined by about 30% for about 1.5 billion stars.

In Bobylev&Bajkova(2021b),using the proper motions of classical Cepheids from the Gaia DR2 catalog based on the linear Ogorodnikov–Milne model, it was shown that there are the following gradients significantly different from zero: ∂U/∂z,∂V/∂z and ∂W/∂x,which behave differently depending on the selection radius.These gradients are closely related to the influence of the warp.In this work,due to the greater accuracy of the proper motions used, we obtain more accurate estimates of the values of these gradients,and more accurate estimates of the residual rotation rates Ωyand Ωx.

The aim of this work is to study the three-dimensional kinematics of the classical Cepheids in the Milky Way.For this, we supplied the Cepheids from Skowron et al.(2019a)with proper motions from the Gaia EDR3 catalog.We apply a variety of kinematic models for the rotation of the Galaxy.Our task is to estimate the parameters of Galactic rotation, as well as to identify the kinematic effects associated with the warp.The main interest of this work is related precisely to the study of the influence of the warp on the kinematics of the Cepheids.Therefore, we are doing everything to use as many of the most distant Cepheids as possible.

The work is structured as follows.An overview of the problem is given in the Introduction.Section 2 describes the nonlinear method for determining the parameters of the Galactic rotation curve 2.1, as well as the linear Ogorodnikov–Milne model 2.2.Data on Cepheids are described in Section 3.The method for generating residual velocities of Cepheids is given in Section4.3.The discussion of the values of the found local parameters ((U, V, W)⊙and |V0|) is in Sections 5.1 and 5.2, the parameters of the Galactic rotation curve are given in Section 5.2, and warp-related parameters in Sections 5.3.2 and 5.3.3.

2.Methods

From observations we have the following values: R.A.and decl.—α and δ,proper motions in R.A.and decl.—μαcosδand μδ, and line-of-sight velocity Vr.From α and δ we go to Galactic longitude and latitude l and b;the heliocentric distance d for Cepheids is calculated on the basis of the period–luminosity relation; we translate the observed proper motions into proper motions in the Galactic coordinate system—μlcosband μb.As a result, we have three components of the spatial velocity of the star: Vrand two projections of the tangential velocity—Vl=k dμlcosband Vb=k d μb, where k=4.74 km s-1,and Vr,Vl,Vbare expressed in km s-1(proper motions are given in mas yr-1(milliarcseconds per year), and the heliocentric distance—in kpc).

In this work, we use a rectangular Galactic coordinate system with axes directed from the observer toward the Galactic center (x axis or axis 1), in the direction of Galactic rotation(y axis or axis 2)and in the direction of the North Pole of the Galaxy (z axis or axis 3).

2.1.Galaxy Rotation Curve

To determine the parameters of the Galactic rotation curve,we use the equations obtained from the Bottlinger formulas,in which the angular velocity Ω is expanded in a series up to terms of the i-th order of smallness d/R0:

where N is the order of the expansion.The quantity Ω0is the angular velocity of rotation of the Galaxy at the solar distance R0,R is the distance from the star to the axis of Galactic rotationR2=d2cos2b-2R0dcosbcosl+R02,the parametersΩi0are the corresponding derivatives of this angular velocity, and the linear velocity of rotation of the Galaxy around the Galactic center in the solar neighborhood is V0=|Ω0|R0.Note that according to the rectangular coordinate system we have chosen,positive rotations are rotations from axis 1 to 2(Ωz),from axis 2 to 3(Ωx), and from axis 3 to 1(Ωy).In this case, the angular velocity of rotation of the Galaxy Ω0is negative.Equations (1)–(3) are written accordingly.This is how they differ from the analogous equations used in the work of Bobylev et al.(2021).In this paper,the value of the distance from the Sun to the Galactic center is assumed to be R0=8.1±0.1 kpc according to the review by Bobylev & Bajkova (2021c).

The system of conditional Equations(1)–(3)is solved by the least squares method (LSM) with weights of the following form:

whereσV r,σV l,σVbare variances of errors of the corresponding observed velocities,and S0is the“sample variance”.The value of S0is comparable to the root-mean-square residual σ0obtained by solving conditional Equations (1)–(3), and in this work it is assumed to be 13 km s-1.

The rectangular components of the spatial velocities of stars are calculated by the formulas

We also use the following two very important velocities: the radial velocity VR, directed from center of the Galaxy to the star, and the velocity Vcirc, orthogonal to VRand directed toward the rotation of the Galaxy, which are calculated using the following formulas:

where the velocities U, V, and W are corrected for the peculiar motion of the Sun U⊙,V⊙,and W⊙,such that the position angle θsatisfies the relation tanθ=y(R0-x).

2.2.Linear Ogorodnikov–Milne Model

In the linear Ogorodnikov–Milne model(Ogorodnikov 1965),the observed velocity of a star V(d),having a heliocentric radius vector d,up to terms of the first order of smallness d/R0≪1,is described by the equation in vector form

where V⊙(U⊙, V⊙, W⊙) is the peculiar velocity of the Sun relative to the grouping of the stars under consideration,V′is the residual velocity of a star, M is a matrix (tensor) of displacements,the components of which are the partial derivatives of the velocity u(u1,u2,u3)with respect to the distance d(d1,d2,d3),

where u= V(R)- V(R0), and R and R0are the galactocentric distances of the star and the Sun, respectively.Then

where the zero means that the derivatives are taken at the point R=R0.All nine elements of the M matrix are determined using three components of the observed velocities—line-of-sight velocity Vr, the velocity along the Galactic longitude Vland that along the Galactic latitude Vb:

To estimate the values of the velocities (U, V, W)⊙and the elements of the matrix M, the system of conditional Equations (9)–(11) is solved by the LSM with weights of the form (4).

Matrix M is divided into symmetric M+(local deformation tensor) and asymmetric M-(rotation tensor) parts:

The components of the rotation tensor are calculated from the elements of the matrix M as follows

The Ogorodnikov–Milne model has been successfully used by many authors to study stellar motions in different planes (Clube 1972; Du Mont 1977; Miyamoto & Zhu 1998; Zhu 2000;Bobylev & Khovritchev 2011; Velichko et al.2020).In this paper,we are mainly interested in the vertical movements of stars.

2.3.Formation of Residual Velocities

We need the residual velocities in order to discard the large discrepancies when determining the parameters of the rotation of the Galaxy.In addition, we need residual velocities to exclude, from the observed velocities, the influence of the differential rotation of the Galaxy in the analysis of effects not related to the rotation of the Galaxy.

The residual velocities of the Cepheids are calculated taking into account the peculiar velocity of the Sun, U⊙, V⊙and W⊙,and the differential rotation of the Galaxy, in the following form:

3.Data

In this work, we use data on classical Cepheids from Skowron et al.(2019a).These Cepheids were observed as part of the fourth stage of the Optical Gravitational Lensing Experiment (OGLE) program (Udalski et al.2015).The Skowron et al.(2019a) catalog contains estimates of distance,age,pulsation period,and photometric data for 2431 Cepheids.Their apparent magnitudes lie in the range of 11m＜I ＜18m,so there is a small deficit of bright and well-studied Cepheids known from earlier observations.

The heliocentric distances up to 2214 Cepheids, d, were calculated by Skowron et al.(2019a) based on the period–luminosity relationship.The specific relationship they used was refined by Wang et al.(2018)from the light curves of Cepheids in the mid-infrared range, where the interstellar absorption is significantly less than in the optical one.The estimates of the age of Cepheids in the work of Skowron et al.(2019a) were made according to the method developed by Anderson et al.(2016),which took into account the periods of axial rotation of stars and the metallicity indices.

We identified 2214 Cepheids with the distances from Skowron et al.(2019a) with the Gaia EDR3 catalog.As a result, a sample of about 2000 stars with proper motions,heliocentric distances, and age estimates was obtained.For about 750 stars from the resulting list, there are line-of-sight velocities from the Gaia DR2 catalog.

As a result, we have a sample of stars with very remarkable characteristics.According to estimates (Skowron et al.2019a),the distances to Cepheids in their catalog are determined with an average relative error of about 5%.This high accuracy was achieved by these authors using infrared data from Spitzer(Benjamin et al.2003; Churchwell et al.2009) and Wide-field Infrared Survey Explorer (WISE, Wright et al.2010; Mainzer et al.2011).The distances to the Cepheids were calculated based on the period–luminosity relation obtained by Wang et al.(2018) for the infrared range.Interstellar extinction was estimated using extinction maps by Bovy et al.(2016).

Random errors of estimates of the line-of-sight velocities of Cepheids from the Gaia DR2 catalog are on average 5 km s-1(see, for example, Figure 1(a)in Bobylev et al.2021).Finally,compared with Gaia DR2, the Gaia EDR3 catalog has about two times better (Gaia Collaboration et al.2021) accuracy in determining the stellar proper motions.Taking the value of the error in determining the proper motion along one of the coordinates equal to 0.03 mas yr-1, we can estimate that the error in the stellar tangential velocity will be about 5 km s-1at a distance from the Sun of more than 15 kpc.We can conclude that we are able to analyze high-precision spatial velocities of Cepheids in a wide range of distances R (up to R ～23 kpc).

4.Results

4.1.Restrictions

Conditional equations in the form (1)–(3) or (7)–(9) are usually solved together using all three components Vr, Vland Vb.True, line-of-sight velocities are not known for all Cepheids.When the star has all three velocities Vr, Vland Vb, then we apply the following restrictions

where the velocities U, V, W are residual, i.e., free from the influence of Galactic rotation.When there are only two velocities Vland Vbfor a star, we apply the following restrictions

We do not use Cepheids, which have a large residual velocity dispersion.These are Cepheids located near the Galactic center in the region of radius R=3 kpc,where the central bar strongly distorts the kinematics of stars.We do not use Cepheids designated in the Skowron et al.(2019a) catalog as OGLE BLG-CEP-XXX—they belong to the bulge, sometimes located at very large heliocentric distances (up to d=25 kpc),far behind the center of the Galaxy.

The distribution of 1847 Cepheids selected using all spatial and kinematic constraints in projection onto the Galactic plane XY is displayed in Figure 1.For the figure,a coordinate system was used, where X is directed from the center of the Galaxy,and the direction of the Y axis coincides with the direction of the previously described Y axis.Note that one Cepheid with distance of Y ～-22 kpc was left behind the frame.The figure shows a four-arm spiral pattern with a pitch angle of -13°(Bobylev & Bajkova 2014); the following segments of the spiral arms are numbered in Roman numerals: I—Scutum-Centaurus Arm,II—Carina-Sagittarius Arm,III—Perseus Arm,and IV—Outer Arm; the central Galactic bar is depicted schematically.The concentration of Cepheids toward the Carina-Sagittarius Arm is clearly visible.

4.2.Galactic Rotation Parameters

Table 1 gives the parameters of the Galaxy rotation,found as a result of the LSM solution of a system of conditional Equations (1)–(3).Restrictions(20)–(21) were applied.The calculations were carried out for five samples with different boundaries of the r distance.

As can be seen from Table 1, the values of the components of the angular velocity of rotation change depending on the radius of the sample.In particular, the value of the linear rotation velocity V0changes slightly from 227 to 236 km s-1.In each case, a rotation curve is perfect for describing rotation in the appropriate range of distances.

The nonlinear model of the Galaxy’s rotation can be applied at any sample radius,having a sufficient number of derivatives in the expansion of the angular rotation velocity.However,the model includes a number of local parameters (to determine which is sufficient, use a small neighborhood R →R0).These are the velocities(U,V,W)⊙and Ω0(and hence V0).It is better to estimate these values on a sample that satisfies the completeness condition in order to obtain unbiased estimates.

The question of the completeness boundary of Cepheids from the catalog of Skowron et al.(2019a) was considered in the work of Bobylev & Bajkova (2021a).It turned out that,depending on the age, these Cepheids are not quite equally distributed.In particular, it was shown that for a sample of Cepheids older than 130 Ma,the completeness limit is 6.5 kpc.Middle-aged Cepheids, from 80 to 130 Myr, are almost all concentrated in the section of the Carina-Sagittarius spiral arm.Finally, for Cepheids younger than 80 Myr, the completeness limit is 4.5 kpc.As a result,in the work of Bobylev&Bajkova(2021a),the value r=5 kpc was adopted,which corresponds to the boundary where the sample of Cepheids under consideration satisfies the completeness condition.However, we believe that we have a sufficient number of Cepheids to reliably determine the parameters of Galactic rotation in a fairly wide range of distances R.

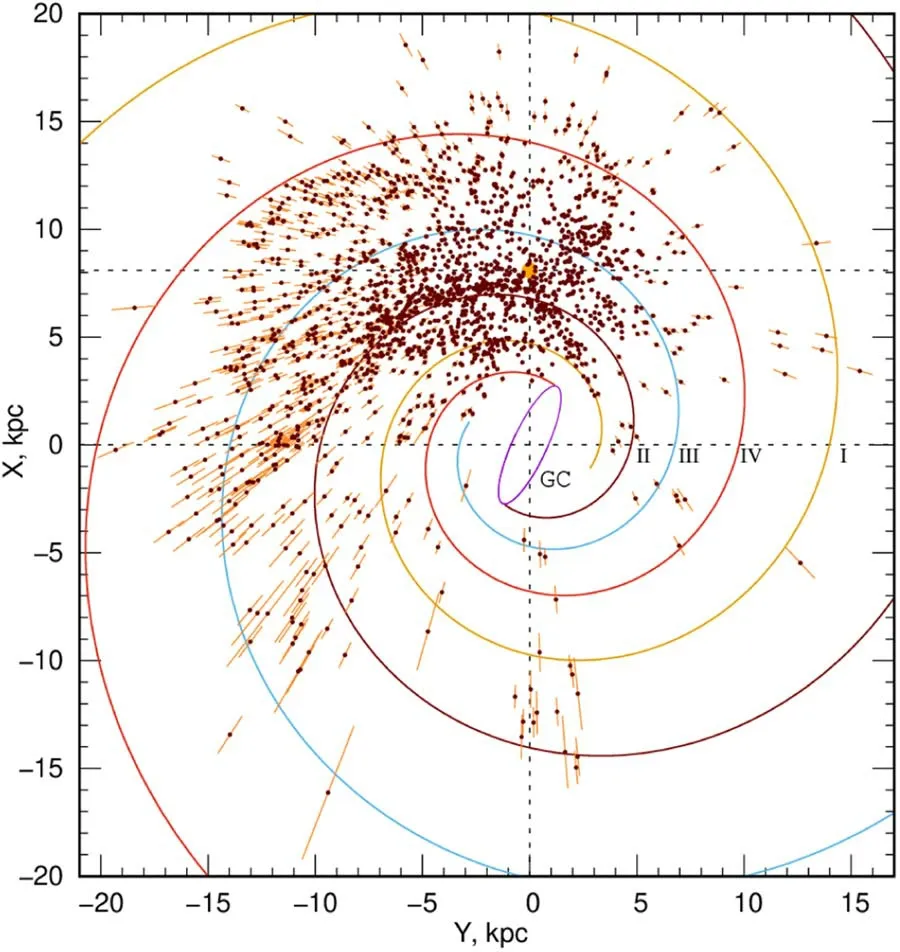
Figure 1.The distribution of Cepheids in the projection on the Galactic plane XY; the position of the Sun is marked with an orange circle (X, Y)=(8.1, 0) kpc,see text.

Table 1 Galaxy Rotation Parameters Found Based on a Nonlinear Model

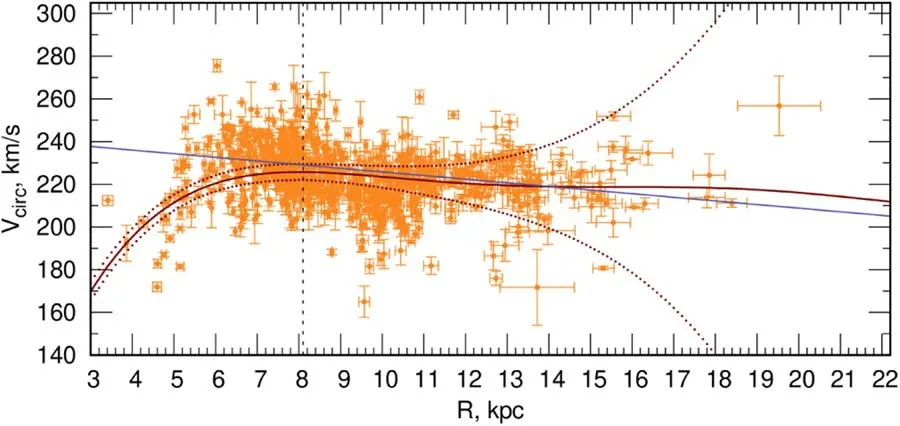
Figure 2.Circular velocities Vcirc of a sample of Cepheids with proper motions and radial velocities.The position of the Sun is marked with a vertical dashed line at distance R0=8.1 kpc,a Galactic rotation curve corresponding to the solution(22)is given,with boundaries indicating the confidence intervals corresponding to the level of errors 1σ, and the blue line signifies the rotation curve from the work of Eilers et al.(2019).

The Galactic rotation curve constructed from the data from the penultimate column of Table 1 (d ≤10 kpc) sharply turns downward at R ～17 kpc.The rotation curve constructed according to the data from the first column of Table 1 also turns down at R ～19 kpc.But in our sample, there are Cepheids located at larger distances.For the study of warp kinematics, the most distant stars are of the greatest interest.

We also obtained a solution using almost the entire sample of Cepheids.In it, in particular, the following values of the velocity of the Sun were found (U⊙, V⊙, W⊙)=(9.39, 15.96,6.88)±(0.40, 0.55, 0.30) km s-1, and also:

where the unit weight error is σ0=12.62 km s-1,and the linear velocity of rotation of the circumsolar neighborhood is V0=225.7±2.9 km s-1for the accepted value R0=8.1±0.1 kpc.Here, 1848 Cepheids from the range of galactocentric distances R: 3-24 kpc were used.

The Galactic rotation curve corresponding to the solution(22)is shown in Figure 2.It is interesting to note that this curve begins to sharply tend upward only at R ～26 kpc.The circular velocities in this figure are given for 732 stars with known proper motions and line-of-sight velocities.We can conclude that the rotation curve corresponding to the solution (22) is flatter at the largest distances R than the curve obtained by us earlier(Bobylev et al.2021)by a similar method from the Mróz et al.(2019) catalog.

Figure 2 also displays the rotation curve from Eilers et al.(2019).This is one of the modern rotation curves of the Galaxy,constructed for a wide range of galactocentric distances.To build it,these authors used highly accurate data on over 23,000 luminous red giant stars, which are distributed over a distance interval of R: 5–25 kpc.These authors found V0=229.0±0.2 km s-1(for adopted R0=8.122 kpc) with a derivative of-1.7±0.1 km s-1kpc-1.As can be seen from this figure,there is good agreement between our curve and the curve from the work of Eilers et al.(2019) both in the solar region, at R=R0, and far in the outer region of the Galaxy.

We decided further to use the solution (22) to form the residual velocities, since the corresponding Galactic rotation curve covers the largest range of distances R: 3–24 kpc.

Figure 3 shows nine dependences of the velocities U, V, W on the corresponding coordinates x,y,z.Figure 3(b)depicts the dependence U=M12·y,where M12corresponds to the angular velocity of rotation of the Galaxy around the axis z (see (13)),M12=∂U/∂y=-Ωz=27.87±0.09 km s-1kpc-1.It can be seen that the points on this graph follow this linear dependence well in a wide range of-10 ＜y ＜10 kpc.But on the other five panels with velocities U and V, the nonlinear character of the velocity distribution is clearly visible.

4.3.Residual Velocity Analysis

Table 2 lists the parameters of the Ogorodnikov–Milne linear model, found as a result of the LSM solution of a system of conditional Equations (9)–(11).In this case, the velocities Vr,Vl,Vbwere corrected for the differential rotation of the Galaxy utilizing the relations(17)–(19),as well as the angular velocity parameters (22).Restrictions (20)–(21) were applied.

Figure 3.Velocities of Cepheids U,V,W vs.heliocentric rectangular coordinates x,y,z.On each panel,the corresponding designations of the deformation matrix Mp,q are given; on panel (b) the gray line shows the dependence U=M12·y, where M12=27.87±0.09 km s-1 kpc-1 corresponds to the solution (22).

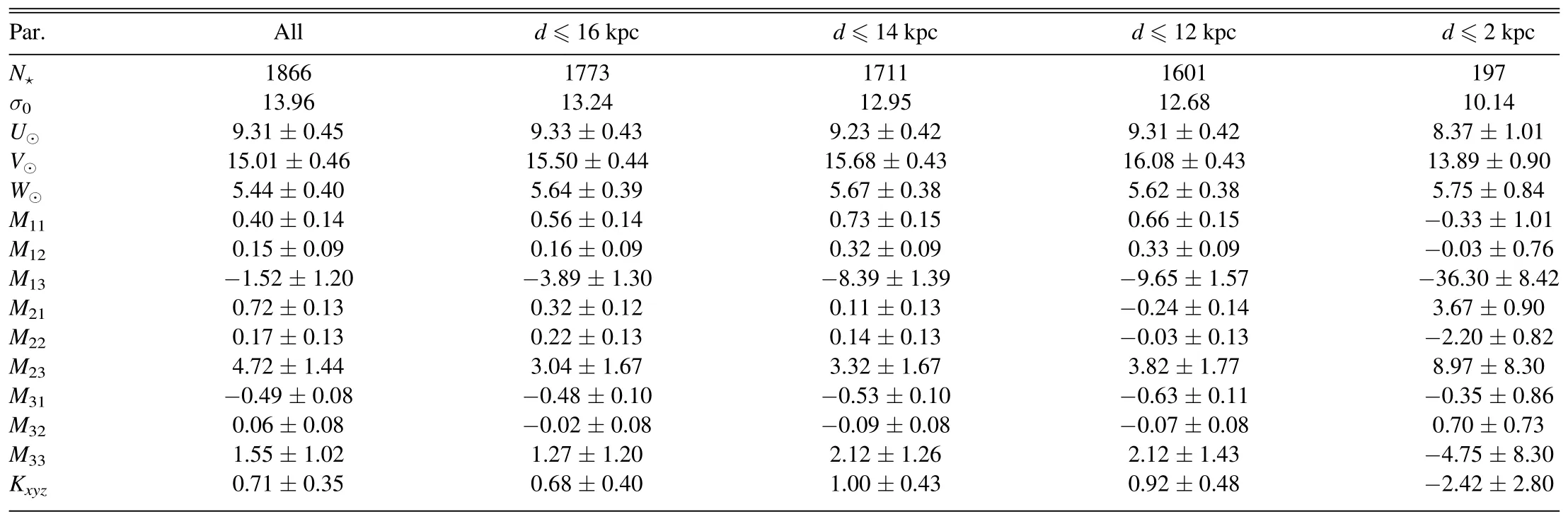
Table 2 Kinematic Parameters of the Complete Linear Ogorodnikov–Milne Model

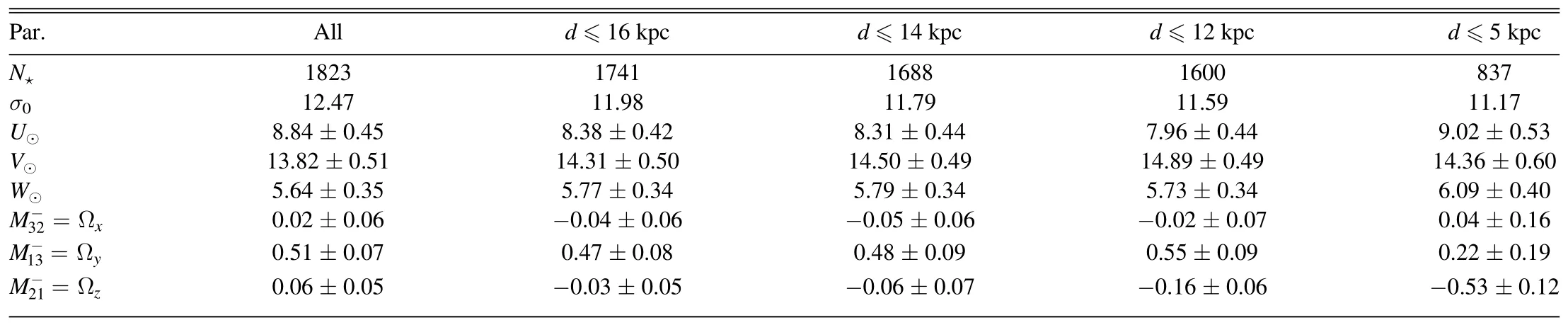
Table 3 Kinematic Parameters of the Rotation Model Found Only from the Proper Motions of the Cepheids

At the top of the table,the number of used stars N★,the error of the unit of weight σ0,found as a result of the LSM solution of a system of conditional Equations (9)–(11), the solar peculiar velocity components(U,V,W)⊙and nine elements of the M matrix(8)are given.The calculations were performed for five samples with different boundaries of the heliocentric distance r.

It is well known (Ogorodnikov 1965) that in studying the rotation of the Galaxy the linear Ogorodnikov–Milne model is applicable up to distances d ≤2 kpc.This can be clearly seen from the behavior of the velocities U and V in Figure 3.Therefore, the last column of Table 2 contains the solution obtained under this constraint.On the other hand,we hope that the analysis of the residual velocities of stars can be carried out at any sample radius.

We also use the simplest pure rotation model.The conditional equations are as follows:

The velocities Vland Vbwere corrected for the differential rotation of the Galaxy utilizing the relations (18)–(19) and constraints(20)–(21).The rotation curve parameters were taken according to the solution (22).

Figure 4 shows nine dependences of the residual velocities U,V, W on the corresponding coordinates x, y, z.In panel(b), the gray line represents the dependence U=M12·y, where M12=0.40±0.14 km s-1kpc-1, and the red line in panel (g)signifies the dependence W=M31·x, where M31=-0.49±0.08 km s-1kpc-1.

Note that the velocities W do not depend on the rotation of the Galaxy.It can be seen that in Figure 4 they are the same as in Figure 3.Moreover, in Figure 3(g), (h) and (i) there is a slightly larger vertical scale in comparison with Figure 4(g),(h)and (i).

We believe that the rotation around the y (M31) axis that we have found is closely related to indirect rather than direct influence of some process that perturbs the vertical velocities of stars.At large distances from the Sun, and at large distances from the center of the Galaxy, there are known processes that perturb the vertical positions and speeds of stars.Such processes include large-scale warp of the Galactic disk, which affects the vertical positions of stars, and its deformation precession, which affects the vertical velocities of stars.Recently, large-scale perturbations of the vertical velocities of stars have also been discovered, which are associated either with the proper oscillations of the disk or with the consequences of the fall of a massive impactor (for example,a dwarf satellite galaxy) onto the disk.Vertical asymmetries have been found in both positions and velocities, and associated with both the Galactic warp and with bending or breathing modes in the disk (Widrow et al.2012; Bennett &Bovy 2019;Carrillo et al.2019;Cheng et al.2020;Chrobáková et al.2022; McMillan et al.2022).

For example, Poggio et al.(2018) demonstrate that the vertical velocities of distant stars begin to increase strongly when R is greater,approximately 12–14 kpc.Thus,estimates of the deformation precession rate turn out to be of the order of 10 km s-1kpc-1(Poggio et al.2020).

We use a linear method of analysis.In this case,we consider both nearby stars, with unperturbed vertical velocities, as well as stars far from the Sun, whose vertical velocities are perturbed.Therefore,we say that our estimates of the gradients reflect the indirect influence of some process that perturbs the vertical velocities of Cepheids.

For example, the green dotted line in Figure 4(g) traces a linear relationship W=-10x-40,where the coefficient,equal to 10 km s-1kpc-1, may reflect the effect of deformation precession.We took the value of this coefficient in accordance with the definition of Poggio et al.(2020).Figure 3(g) shows even better that for x ＜-4 kpc the horizontal distribution of velocities W is replaced by a rather sharp rise.

Figure 4.Velocities of the Cepheids U,V,W(corrected for the rotation of the Galaxy with parameters(22))vs.the heliocentric rectangular coordinates x,y,z.In panel(b),the gray line shows the dependence U=M11·x,where M11=0.40±0.14 km s-1 kpc-1,and the red line on panel (g)represents the dependence W=M31·x,where M31=-0.49±0.08 km s-1 kpc-1.

5.Discussion

5.1.Peculiar Velocity of the Sun

The velocities (U, V, W)⊙are the group velocity of the considered sample of Cepheids, taken with the opposite sign.These velocities contain the peculiar motion of the Sun relative to the local standard of rest, disturbances from the spiral density wave (for relatively young objects), and the influence on the velocity V⊙of the so-called asymmetric drift(lagging behind the circular velocity of rotation with the age of the sample).

Asymmetric drift (Strömberg 1946) manifests itself in the fact that the velocity in the direction of Galactic rotation, V,systematically increases with the square of the stellar velocity dispersion.The value of the correction for asymmetric drift,Vasym, strongly depends on the age of the sample stars.For example,according to Bensby et al.(2003)Vasymis:-15,-46 and -220 km s-1for the thin disk, thick disk and halo,respectively.

The components of the solar peculiar velocity relative to the local standard of rest are determined rather carefully in the work of Schönrich et al.(2010), and are (U, V, W)⊙= (11.1,12.2, 7.3)±(0.7, 0.5, 0.4) km s-1.

We note the work Tian et al.(2015), which reports a kinematic analysis of about 200,000 relatively close to the Sun FGK-type main-sequence stars selected from LAMOST (Cui et al.2012;Deng et al.2012;Zhao et al.2012).These authors found values (U, V, W)⊙= (9.58, 10.52, 7.01)±(2.39, 1.96,1.67) km s-1, close to Schönrich et al.(2010).

Huang et al.(2015) analyzed FGK dwarfs from the LAMOST catalog using their line-of-sight velocities and proper motions.The stars were taken from the circumsolar region with a radius of about 600 pc.In particular,these authors found (U, V, W)⊙= (7.01, 10.13, 4.95)±(0.20, 0.12, 0.09)km s-1.

It is interesting to note the work Coşkunoğlu et al.(2011),where a sample of 18,026 high-probability thin-disk dwarfs within 600 pc of the Sun from the RAdial Velocity Experiment(RAVE, Steinmetz et al.2006) spectroscopic survey was analyzed.The RAVE survey is distinguished by high-precision line-of-sight velocities of stars, which are determined with average errors of about 2 km s-1.The proper motions of the stars here were taken from various catalogs.These authors found (U, V, W)⊙= (8.50, 13.38, 6.49)±(0.29, 0.43, 0.26)km s-1.The velocity (U, V, W)⊙values we found are in very good agreement with the results of Schönrich et al.(2010)and Coşkunoğlu et al.(2011).

In Mróz et al.(2019), when analyzing about 770 Cepheids from the list of Skowron et al.(2019a)with known line-of-sight velocities, the values (U, V, W)⊙= (10.1, 12.3, 7.3)±(1.0,2.1, 0.7) km s-1(Model 2 with prior on R0).

Bobylev et al.(2021), when analyzing about 800 Cepheids from the list of Skowron et al.(2019a)with known line-of-sight velocities, found the values (U, V, W)⊙= (10.1, 13.6,7.0)±(0.5, 0.6, 0.4) km s-1on the basis of the nonlinear model of Galactic rotation.

The values of the velocities (U, V, W)⊙found by us are in good agreement with these estimates.As you can see from Tables 1, 2 and 3, all three components of this velocity are stable under different constraints on the distance r.Note the values (U, V, W)⊙= (9.56, 13.96, 6.85)±(0.46, 0.71, 0.41)km s-1from the last column of Table 1, obtained from the sample Cepheids satisfying the completeness condition,as well as (U, V, W)⊙= (9.02, 14.36, 6.09)±(0.53, 0.60, 0.40) km s-1from the last column of Table 3 obtained under a similar condition using only proper motions from the Gaia EDR3 catalog.Cepheids are relatively young stars(the average age of the sample is about 110 Ma), therefore, they do not have a noticeable shift in ΔV⊙due to asymmetric drift compared to the result, for example, of Schönrich et al.(2010).

5.2.Rotation of the Galaxy

Linear velocity V0is the most important local parameter.In our case,the most interesting is its value|V0|=236.3±3.3 km s-1(for the accepted value R0=8.1±0.1 kpc),indicated in the last column of Table 1.This estimate is unbiased, since it was found from a sample of Cepheids that satisfies the completeness condition.

Mróz et al.(2019), when analyzing 770 Cepheids from the list of Skowron et al.(2019a) with known line-of-sight velocities, obtained the estimate |V0|=233.6±2.8 km s-1(for the accepted value R0=8.122±0.031 kpc).

Bobylev et al.(2021)analyzed about 800 Cepheids from the list of Skowron et al.(2019a) with known line-of-sight velocities using a nonlinear rotation model of the form (1)–(3) and obtained |V0|=240±3 km s-1for the found value R0=8.27±0.10 kpc.

It is also interesting to note the work of Ablimit et al.(2020),where about 3500 classical Cepheids with proper motions from the Gaia DR2 catalog were utilized to construct the rotation curve of the Galaxy.The rotation curve of the Galaxy was plotted in the range of distances R: 4–19 kpc.The circular velocity of rotation of the near-solar neighborhood was found with a very high accuracy;its value was|V0|=232.5±0.9 km s-1for the accepted value R0=8.122±0.031 kpc.

On the other hand, to form the residual velocities and analyze the kinematics of the most distant Cepheids in the sample, it is necessary to use the rotation curve (22) or the parameters from the first columns of Table 1.As noted above,the rotation curve (22) is good because it is close to flat(Figure 2) over a very large range of distances R.It is applicable over the entire R interval where the Cepheids of our sample are present, so there is no need to use alternative approaches.By alternative we mean, for example, a flat rotation curve (V0= const ), or obtained in some potential(curve (18) in Bobylev et al.2021).

To determine the parameters of the Galaxy rotation, in addition to Cepheids,a wide variety of Galactic objects is used.For example, Dias &Lépine (2005) considered kinematic data on 212 open star clusters primarily to estimate the parameters of the spiral pattern.In this case, the estimate |V0|=190 km s-1was obtained for the accepted R0=7.5 kpc.

In Bovy et al.(2012), to determine the parameters of the Galaxy rotation in the distance range R:4-14 kpc,the line-ofsight velocities of 3365 stars from the SDSS-III/Apache Point Observatory Galactic Evolution Experiment (APOGEE) spectroscopic survey(Wilson et al.2010)were used.They obtained an estimate |V0|=218±6 km s-1for the foundR0= 8.1kpc.

In López-Corredoira (2014), proper motions of a huge selection of red clump giants from the PPMXL catalog (Röser et al.2010) were considered.For these stars, photometric distances were determined.As a result, an estimate |V0|=238 km s-1was obtained for the accepted R0=8 kpc and a rotation curve of the Galaxy was constructed in the range of distances R: 4–16 kpc.The rotation curve turned out to be close to flat over the entire analyzed R range.In this case,a strong decrease in the circular velocity of Galactic rotation with height was found for |z|≈2 kpc and R ≈16 kpc.

Galazutdinov et al.(2015) concluded that the rotation curve of the thin gaseous disk of our Galaxy is Keplerian rather than flat.For this, data on distances and line-of-sight velocities obtained from observations of the interstellar lines Ca II H and K were used.Such observations, after calibration of Megier et al.(2009) by the trigonometric parallaxes of the Hipparcos catalog, determine a unique scale of distances to stars.According to estimates by Megier et al.(2009), the accuracy of determining distances to OB stars by this method is about 15%.With all this, Galazutdinov et al.(2015)'s conclusion about the Keplerian nature of the rotation curve of the Galaxy contradicts the rotation curve of the Galaxy obtained in this work (which is close to flat).

It is interesting to note the work of Chrobáková et al.(2020),where the rotation curve of the Galaxy was constructed using the kinematic data on stars from the Gaia DR2 catalog via the Jeans equation.These authors showed that in the outer region of the Galaxy the rotation curve they found in the range of distances R:8–18 kpc is very close to flat and depends little on R and z.

Reid et al.(2019) reported the following values for the two most important kinematic parameters for a sample of 147 masers:R0=8.15±0.15 kpc and Ω⊙=-30.32±0.27 km s-1kpc-1,where Ω⊙=Ω0+V⊙/R.The velocity value V⊙=12.24 km s-1was referenced from Schönrich et al.(2010).These authors used a series expansion of the linear velocity of the Galaxy rotation.

Based on a similar approach, VERA Collaboration et al.(2020)obtained the following estimates from an analysis of 99 masers observed using the VERA program: R0=7.92±0.16(stat.)±0.3(system)kpc and Ω⊙=-30.17±0.27(stat.)±0.3(system)km s-1kpc-1, where Ω⊙=Ω0+V⊙/R, and the velocity value V⊙=12.24 km s-1was also taken from Schönrich et al.(2010).

From the analysis of 788 Cepheids from the list of Mróz et al.(2019) with proper motions and line-of-sight velocities from the Gaia DR2 catalog, Bobylev et al.(2021) found (U⊙,V⊙, W⊙)=(10.1, 13.6, 7.0)±(0.5, 0.6, 0.4) km s-1, and also:

where|V0|=240.2±3.2 km s-1and R0was also considered as the unknown variable.In Figure 5 from the work of Bobylev et al.(2021), one can see that the rotation curve (25) for the formation of residual stellar velocities is suitable for distances R less than 18–19 kpc.

5.3.Linear Model Parameters

5.3.1.Plane XY

Consider the displacement tensor describing the residual rotation around the z axis.Let us denote this tensor as Mxy,since its elements are the partial derivatives of the velocities U,V with respect to x and y

The elements of this tensor can be written in terms of the wellknown Oort constants (A, B, C, K)xy, which in our case describe the residual effects

According to the data from the second column of Table 1, we have (matrix elements are given in km s-1kpc-1)

on the basis of which we find Axy=0.24±0.08 km s-1kpc-1,Bxy=0.08±0.08 km s-1kpc-1, Cxy=0.17±0.10 km s-1kpc-1and Kxy=0.39±0.10 km s-1kpc-1.

In a similar approach, using these Cepheids for the proper motions from the Gaia DR2 catalog, Bobylev & Bajkova(2021b) found Axy=-0.13±0.11 km s-1kpc-1,Bxy=-0.13±0.11 km s-1kpc-1, Cxy=0.43±0.11 km s-1kpc-1and Kxy=0.25±0.11 km s-1kpc-1.We see that there is no particular repeatability of the results.Most likely, there are random fluctuations of the velocity field of distant Cepheids.However, M11=∂U/∂x is always significantly different from zero, as you can see from Table 2.

5.3.2.Plane YZ

Consider the displacement tensor Myz

According to the data from the first column of Table 1 we have

On the other hand, the gradient ∂V/∂z(M23) differs significantly from zero only in the first column of Table 1.For example, according to the data from the second column of Table 1 we have

We can conclude that in terms of the velocities of distant Cepheids, the residual kinematic effects in the YZ plane are negligible.

5.3.3.Plane XZ

Here the displacement tensor Mxzlooks like this

First, we note the results from the last column of Table 2,obtained for d ≤2 kpc.The large value of M13=-36.30±8.42 km s-1kpc-1is striking.For this case, we have

As a result,we can conclude the following:Compared to the analysis of a similar sample of Cepheids with proper motions from the Gaia DR2 catalog carried out by Bobylev & Bajkova(2021b), the values of the gradients M13=∂U/∂z and M23=∂V/∂z have significantly decreased.Their values highly depend on the residual velocities of the stars.In this work, we found that when the most distant Cepheids are included in the consideration, the values of these gradients do not differ significantly from zero.

6.Conclusion

The three-dimensional motions of a large sample of classical Cepheids of the Milky Way are analyzed.For this, the Cepheids from Skowron et al.(2019a) were used.After identifying these stars with the Gaia EDR3 catalog,a sample of about 2000 stars with proper motions, heliocentric distances and estimates of their ages was obtained.For some of these stars,the line-of-sight velocities are known from the Gaia DR2 catalog.

The parameters of the rotation curve of the Galaxy are determined on the basis of a nonlinear rotation model.In particular, it is shown that the Galactic rotation curve corresponding to the solution (22) is flat over a very wide range of distances, up to R ～24 kpc.It can be recommended,for example,for obtaining the residual velocities of stars when performing spectral analysis of the residual velocities of stars and other similar works.Thus, we used the parameters (22) to form the residual velocities of Cepheids located in a wide range of distances R: 3–18 kpc.

The parameters of rotation of the Galaxy obtained from more nearby Cepheids are of interest.Thus, considering stars from the region with a radius of d=5 kpc (this sample of Cepheids satisfies the completeness condition), the circular linear velocity of rotation of the circumsolar neighborhood around the center of the Galaxy was found as V0=236±3 km s-1for the accepted distance R0=8.1±0.1 kpc.

Application of the linear Ogorodnikov–Milne model to the analysis of residual velocities of Cepheids showed the presence of the gradients ∂U/∂x, ∂U/∂z, ∂V/∂x, ∂V/∂z and ∂W/∂x significantly different from zero.These gradients behave differently depending on the selection radius d and constraints on the radius R.

The most interesting is the gradient ∂W/∂x, since the velocities of W are free of Galactic rotation.Its value is～-0.5±0.1 km s-1kpc-1, which can be interpreted as the positive rotation of this star system around the Galactic axis y,i.e.,rotation with angular velocity Ωy.A more accurate estimate of Ωy=0.51±0.07 km s-1kpc-1is obtained on the basis of a simpler model of pure rotation.In our opinion, this rotation around the y axis reflects the indirect influence of some process that perturbs the vertical velocities of Cepheids.

Note that the ∂W/∂x gradient can be explained in many ways,not necessarily by deformation precession;for example,such as bending + breathing modes, fusion and interaction with satellites, changes in the amplitude of deformation (not only its precession), disequilibrium due to the violent origin of the Galactic disk and others(Laporte et al.2018;Wang et al.2018).

It is shown that on the scales under consideration (d ＞12 kpc), there is no significantly different from zero rotation around the Galactic axis x.The volumetric expansion/contraction of the Cepheid system was not found to be significantly different from zero, i.e., Kxyz=0.