Collaborative Simulation of Mechanical Structure and Control Systems of Leighton Chajnantor Telescope

Yi-Wei Yao, Wei-Rui Chen , and Zheng Wang

School of Automation, Southeast University, Nanjing 210096, China; wangz@seu.edu.cn

Abstract Leighton Chajnantor Telescope (LCT) will be moved from the summit of Maunakea, Hawaii to Chajnantor Plateau, Chile and be refurbished there.Strong wind disturbance at the new site will bring great challenges to the servo control of LCT.It is necessary and important to develop a simulation platform that behaves as close as possible to the real telescope for testing the performance of the designed servo controller.In this paper, a collaborative simulation platform of LCT based on Adams and Matlab/Simulink is constructed.On this platform,the mechanical structure model of LCT can be integrated with its control system model such that a collaborative simulation of the mechanical structure and the control system of LCT can be conducted.The mechanical structure model of LCT,which contains both rigid body models(i.e.,the mount)and flexible body models(i.e.,the primary reflector),is developed by using Adams.The servo system model and the wind disturbance model are constructed by using Matlab/Simulink.By conducting collaborative simulation,the performances of the servo controller based on the rigid body model and the rigid-flexible coupling model of LCT are compared.The comparison shows that the controller designed based on the rigid body model does not perform well when it is employed to control the rigid-flexible coupling model of LCT.However,by readjusting parameters of the servo controller,its performance can be further improved when applied to the rigid-flexible coupling model.Therefore,an LCT model of integrated mechanical structure and control systems is very helpful for analyzing its performance more accurately and designing a better servo controller.

Key words: telescopes – submillimeter: general – techniques: miscellaneous

1.Introduction

Leighton Chajnantor Telescope(LCT),formerly the Caltech Submillimeter Observatory (CSO) telescope, has a primary reflector of 10.4 m in diameter and works at the wavelengths from 350 μm to 2 mm.By observing at submillimeter wavelengths with the help of LCT, the process of star formation in molecular clouds of distant galaxies can be effectively studied(Groesbeck 1995).LCT will be moved from the summit of Maunakea, Hawaii to Chajnantor Plateau, Chile and be refurbished there.To further improve the observation capability of LCT, higher requirement on the performance of servo control will be satisfied.For example, its pointing accuracy is required to be improved from 3″(rms)to 1″(rms),and the rotating speed needs to increase from 1°s−1to 2°s−1.In addition, Chajnantor Plateau is at an altitude of 5050 m and has an average wind speed of 10 m s−1in winter.1https://almascience.nrao.edu/aboutalma/weather/overviewThe wind force acting on the 10.4 m diameter primary reflector of LCT brings disturbance to the servo control system and poses a great challenge to the servo controller.To analyze the performance of the servo controller under wind disturbance, it is necessary to develop a collaborative simulation platform containing the control system model and the mechanical structure model,along with the wind disturbance model.

Many mechanical structure models of radio telescopes have been constructed for simulation and analysis.Some researches focus on the static mechanical analysis of radio telescopes,i.e.,thermodynamic analysis(Johnston et al.2004),or deformation and stress analysis by wind (Vogiatzis et al.2004) or gravity(Zuo et al.2011).Mathematical models and finite element models of the main reflector of the RT-70 radio telescope were constructed to analyze the temperature fields in different climate conditions (Borovkov et al.2003).Vial et al.(2020)simulated the distribution of the stress and the deformation of LCT under the strong wind of 10 m s−1at the position of 30°in azimuth and 45°in elevation based on the finite element model.With the help of Patran(an FEM analysis tool),Fu et al.(2017)developed the finite element model of the TM65m telescope and investigated the effect of gravitational deformation on the surface accuracy of the primary reflector and the pointing accuracy by simulation and experiment.In addition, some researches are conducted on the dynamical response of telescopes.A detailed finite element model of the NASA's next generation space telescope (NGST) contains beam components, thin-surface shell-type components, revolute and prismatic joints and reaction wheels, and has three types of dynamic characteristics, i.e., vibrational response, attitude control and deployment (Wasfy & Noor 2000).

On the other hand, there were a lot of researches on control system modeling and analysis of telescopes.Phuong et al.(2018) modeled the electromechanical system of the RT-70 telescope and proposed a servo drive system with discrete-time model predictive controller based on Laguerre functions.A linear optimal controller was also designed for rotating speed control in azimuth(Belov&Phuong 2017).Hodge et al.(1992)developed the control system of a gimballed large diameter(3.5 m) ground-based telescope and evaluated the tracking performance using the rigid-body time-domain simulation model.In control system models, the mechanical structures of radio telescopes are usually considered as rigid bodies due to the convenience for theoretical analysis and the difficulties of building finite element models in control system simulation tools.

In the previous works on analyzing the control system of LCT, the flexibility of its structure was not taken into consideration, which will lead to two problems.First, the vibration caused by the flexible structure of the telescope could bring significant impacts on pointing accuracy and surface accuracy of the telescope, but this is not accurately modeled.Second, an inaccurate mechanical structure model will lead to the degrading of the performance of the model-based controller when applied to the real telescope, because it relies on the accuracy of the model very much.A lot of extra time will be needed to redesign the controller, which is originally designed based on the rigid body model,such that it can be applied to the real telescope.In this research, a collaborative simulation platform is developed for the design of the new controller of LCT by introducing the detailed rigid-flexible coupling model of the mechanical structure of the telescope into its control system model and by the collaborative working of Adams (a tool for multibody system analysis)(Schiehlen et al.1990)and Matlab/Simulink (a tool for control system simulation).

This paper is organized as follows: in Section 2, the mechanical structure model of LCT is introduced,including the modeling methods and processes for modeling the rigid and flexible structures.In Section 3, the collaborative simulation platform is developed, including the modeling of the control system, the modeling of wind disturbance and the method of collaborative simulation.In Section 4, experiments and analysis based on the collaborative simulation platform are presented.Section 5 concludes the paper.

2.Structural Modeling of LCT

Figure 1.The mechanical structure model of LCT:(1)secondary reflector and supporting legs, (2) primary reflector, (3) spaceframe backup structure, (4)reflector mounting platform,(5)counterweight arms,(6)elevation axis support arms, (7) central body, (8) working platform, (9) teepee, and (10) mount.

The structure of LCT consists of the primary reflector, the secondary reflector and supporting legs,the spaceframe backup structure, the reflector mounting platform, the counterweight arms, the elevation axis support arms, the central body, the working platform, the “teepee”, and the mount.The compositions of LCT structure are presented in Figure 1.The mechanical structure model of LCT is reconstructed based on the original SolidWorks model developed by the engineers from Chilean Teams of the LCT Project (see Acknowledgements).

Most of the structural components of LCT are modeled as flexible bodies, but some components are simplified as rigid bodies in order to reduce calculation consumption.To ensure that the simplified rigid-flexible coupling LCT model is within the margin of error, when selecting the rigid bodies, we considered three main perspectives: (1) the deformation of the rigidized components,(2)the impact of component rigidization on the reflector, and (3) the impact of component rigidization on the servo control system.Components that can be simplified as rigid bodies should be structurally stable and slightly deform under the wind and the gravity.The deformation of the components that are simplified as rigid bodies should not cause the displacement or the deformation of the core components such as the primary reflector and the secondary reflector.For the servo control system,the components that are simplified as rigid bodies should not significantly affect the rotational inertia of LCT and should not change the fundamental frequency of vibration modal in azimuthal rotation.Taking these three perspectives into consideration, many simulation experiments about the deformation analysis and vibration modal analysis of LCT are performed.Finally, the components chosen to be simplified are the mount and the working platform,because the deformation of the mount under the wind and the gravity is very slight and the vibration frequency of the telescope is not significantly influenced by the rigidization of the working platform.

The overall model of LCT is constructed by Adams,which is a very often-used multibody system analysis tool.However,because Adams is not very good at building complex structural bodies, the mechanical structure of LCT is constructed by SpaceClaim, which is a 3D modeling tool contained in Ansys.The rigid bodies created by SpaceClaim are directly imported into Adams.The flexible bodies are first divided into finite elements in Ansys,based on which the modal neutral file of the flexible bodies is obtained by conducting modal analysis.The flexible bodies are generated in Adams by importing the modal neutral files created in Ansys.Finally, the fixed joints are applied in Adams between the contact surfaces of the flexible bodies and the rigid bodies to connect all the parts as a whole for later simulations.

2.1.Rigid Body Modeling

The rigid bodies mainly consist of two parts, i.e., the working platform and the mount.The working platform has an approximate semi-circular shape with a radius of 3.74 m.It contains two parts, i.e., the receiver room and the compressor platform.The receiver room is used to store scientific instruments.The compressor platform holds the helium compressor for 4 K closed-cycle refrigerators.To simplify the model, the bottom of the platform is modeled as a rigid semi-circular solid with the thickness of 15.8 mm.Since the mass of the receiver room and the helium compressor will affect the rotational inertia in azimuth,they are modeled by the solids of corresponding thickness.The corresponding solid thickness of the receiving room is 13.6 mm and the thickness of the helium compressor is 49 mm.The mount is connected to the azimuth bearings of the telescope.It supports the telescope's weight and fixes the telescope's body.The mount contains the tail bearing seat, the mount body, and four mount legs.Because the mount part is fixed on the ground, the modeling of the mount ignores the small details, like the four mount feet.The rest of the part is modeled as a rigid solid.The rigid models of mount and platform are shown in Figure 2.

2.2.Flexible Body Modeling

The flexible bodies are divided into three main parts,i.e.,the elevation axis motion part, the azimuth axis motion part, and the fixed part.The elevation axis motion part includes the secondary reflector and supporting legs, the primary reflector,the spaceframe backup structure, the reflector mounting platform and the counterweight arms.The azimuth axis motion part includes the elevation axis support arms and the central body.The fixed part includes the“teepee.”The components in the same part are modeled separately and then connected into a whole for calculation and analysis.Flexible body modeling is realized in the following four steps:

2.2.1.Finite Element Modeling

The finite element model of LCT's flexible bodies is obtained by meshing the structural model.Typically, solid structural models are meshed using solid elements, which will generate more nodes and cost more computing time.However,using corresponding simplified elements according to the structural features can greatly reduce the number of nodes and the computing time.In LCT's model, single-layer shell elements are used to simplify the steel panels and singlecolumn beam elements are used to simplify the steel pipes.

Take the primary reflector as an example for shell elements modeling.The primary reflector is 10.4 m in diameter and 4.12 m in focal length, which is composed of hexagonal honeycomb aluminum panels with the edge length of 0.664 m.Since the gaps between panels are very small(about 2 mm),the primary reflector is simplified to a single surface.The thickness of the honeycomb aluminum panel is about 23.5 mm,which is much smaller than the size of the aluminum panel.Therefore,it is reasonable to simplify the primary reflector by shell elements due to the specific ratio of thickness to span (less than 1/15).

The parabolic-shape surface of the primary reflector is created in SpaceClaim, which can be formulated as

where p=4.12 m is the focal length of the primary reflector.

The parabolic surface of the primary reflector is meshed with shell elements.The finite element model of the primary mirror is composed of 1802 elements and 1845 nodes.The material is customized as honeycomb aluminum with the density of 603 kg m−3, the Young’s modulus of 7×1010Pa, and the Poisson’s ratio of 0.33.The meshed primary reflector is shown in Figure 3.

Figure 2.The rigid models of the mount (left) and the platform (right).

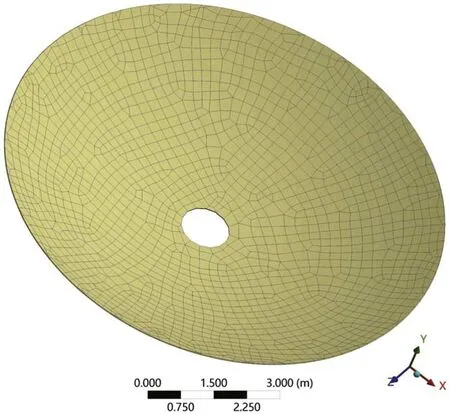
Figure 3.The meshed primary reflector.

We take the spaceframe backup structure of the primary reflector as another example for beam elements modeling.As shown in Figure 4, the spaceframe backup structure, observed along the optical axis, is a regular triangular grid with edge length of 0.664 m.Observed along the cross section,it consists of two layers of nodes.The set of nodes closer to the primary reflector is located on a parabolic surface with the same curvature as the primary reflector and are connected to primary reflector through 15 cm long vertical steel pipes parallel with the optical axis.The layer of nodes farther from the primary reflector,which is also approximately arranged on a paraboloid surface,is connected to the nodes near the primary reflector one by one through steel pipes parallel with the optical axis.The nodes in the central area are fixed on the reflector mounting platform.There are also horizontal steel pipes connecting neighboring nodes on the same layer and diagonal pipes on different layers, as shown in Figure 5.To balance rigidity and weight, the material of the steel pipes is classified into four levels (Woody et al.1994).The closer to the central axis, the thicker the steel pipes are.It is reasonable to simplify the pipe with a ratio of cross-sectional length to pipe length less than 1/20 with beam elements.Pipes of the spaceframe backing structure meet the requirement.

The wireframe of the spaceframe backup structure (Vial et al.2020) is imported into SpaceClaim with given cross sections.Then,the wireframe is meshed with beam elements in Ansys.The number of nodes is 1917 and the number of elements is 2601.Levels, cross sections and materials of pipes are listed in Table 1.

The element types,total number of elements,total number of nodes,and materials of other components of LCT are shown in Table 2.To improve the accuracy of the model, easily deformed components (e.g., the connections between components) are meshed densely, and less deformed components(e.g., the counterweights) are meshed sparsely.

After modeling each component, components of each part need to be integrated together.Since shell and beam element nodes have the same six degrees of freedom(displacement in x, y, z direction and rotation around x, y, zaxis), shell-to-shell elements and shell-to-beam elements are integrated together by nodes sharing.However, solid element nodes lack rotational degrees of freedom compared to shell and beam element nodes, multi-point constraints (MPC)method is used to integrate solid elements with shell or beam elements.

The finite element model of LCT is shown in Figure 6.The model uses Solid186 elements, Shell181 elements and Beam188 elements.The total number of elements is 21 102 and the total number of nodes is 26 975.

2.2.2.Build Remote Point

To simulate the forces acting on contact surfaces in LCT's mechanical structure model in Adams, it is necessary to introduce some remote points and associate them with the surfaces that are externally stressed or contacted.By using the remote points, the force can be uniformly distributed to each node on its associated surfaces.For example,two remote points are created for the elevation axis motion part,among which one is associated with the primary reflector surface for simulating the wind force, and the other is associated with the elevation axis bearing for creating a revolute connection with the elevation axis support arms.

2.2.3.Modal Analysis

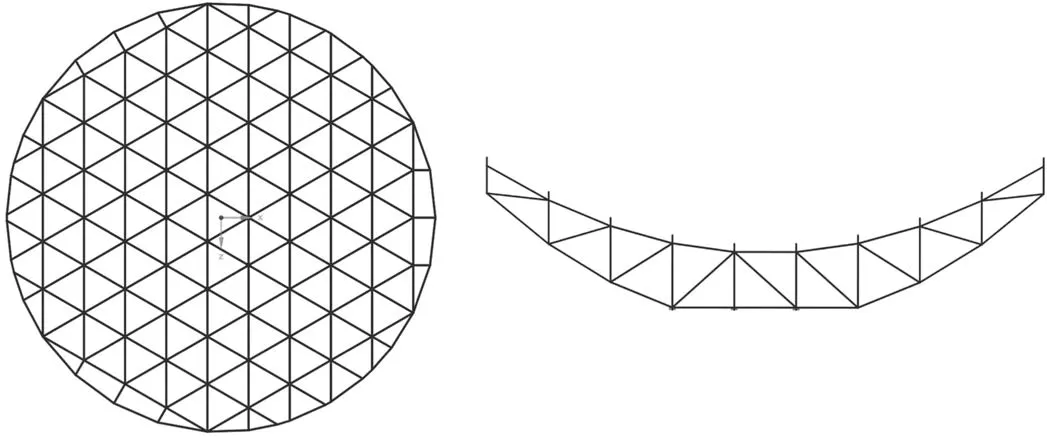
Figure 4.The plan view of the spaceframe backing structure (left) and the cross section of the spaceframe backing structure (right).

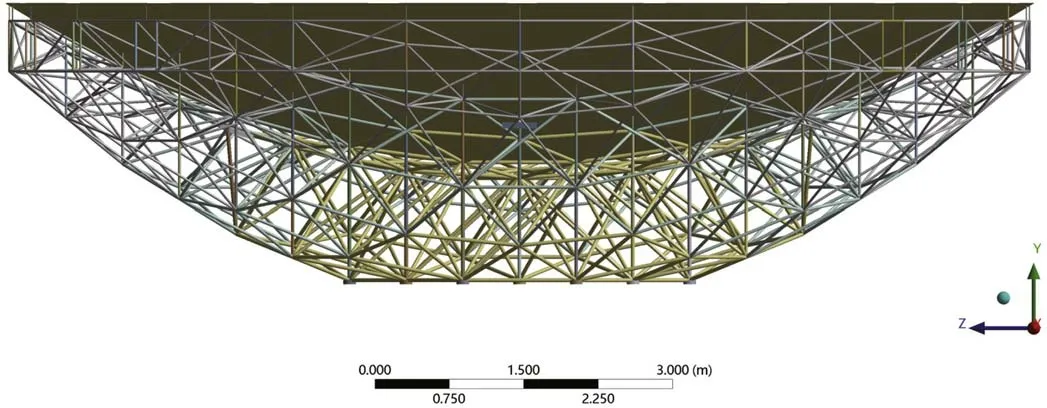
Figure 5.The general view of the spaceframe backing structure.

Table 1 Levels, Cross Sections, and Materials of Pipes

The purpose of the modal analysis is to obtain the natural frequencies and modal shapes of LCT's parts that consists of flexible bodies.In this subsection, we consider free vibrations of the LCT's part with N degrees of freedom without damping and external input.The differential equation of motion is as follows (Gawronski 2004):

where q is the N×1 displacement vector of nodes;q¨ is the N×1 acceleration vector of nodes;M is the mass matrix and K is the stiffness matrix.The generalized eigenvalue equation of the above is:

The necessary and sufficient condition for the above equation to have a non-zero solution is that its determinant is zero, that is:

The frequencies that satisfy the above equation are denoted by ω1,…,ωnwhich are called the natural frequencies.Substituting ωiinto the equation yields the corresponding vectors φ1,φ2,…,φn.The ith vector φicorresponding to the ith natural frequency ωiis called the ith modal type.The first nine natural frequencies of the three parts of LCT are shown in Table 3.The modal shapes of the elevation axis motion part are shown in Figure 7 as an example.Flexible bodies of LCT can be imported into Adams via modal neutral files (.mnf), which are generated from modal analysis results.The modal neutral file contains the following information (Wallrapp 1994): (1)coordinates of the nodes, (2) mass of the nodes, (3) naturalfrequencies and mode shapes, (4) the mass matrix and the stiffness matrix, and (5) remote points.

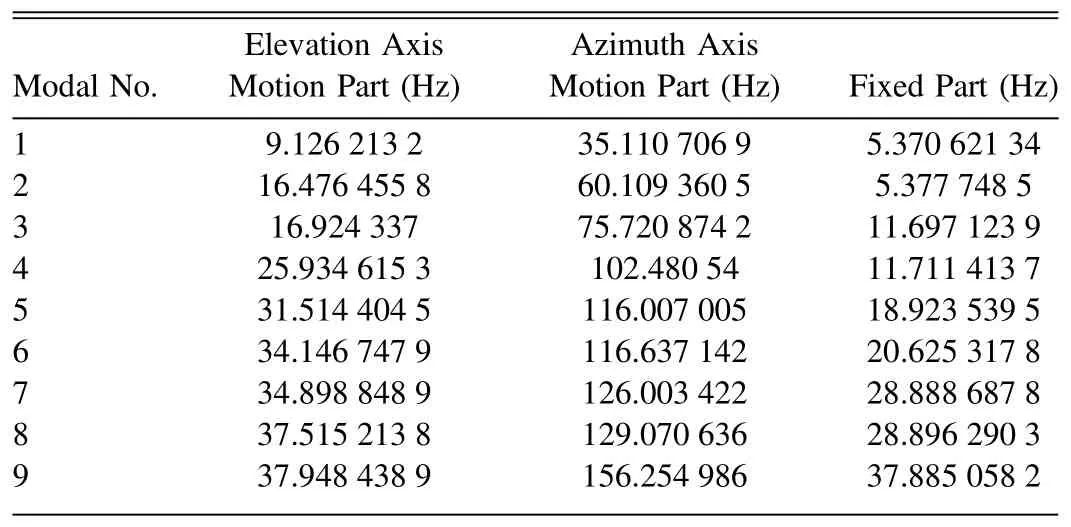
Table 3 First Nine Natural Frequencies of the Three Parts of LCT

2.2.4.Generation of Flexible Bodies in Adams

By importing the.mnf file to Adams, we can generate the flexible bodies.The model can be simplified by disabling the modals unrelated to azimuthal motion and the modals caused by small local structures.Vibrations of the flexible body can be simulated based on the simplified model.

Based on the rigid bodies and flexible bodies built above,the rigid-flexible coupling structural model of LCT can be constructed.To connect the rigid bodies with the flexible bodies,the fixed joints are applied between the remote points of the flexible bodies and the rigid bodies.Through fixed joints,the degree of freedoms of the nodes of the flexible bodies connected to remote points is constrained by the rigid body parts.In this way, the effect of the rigid bodies is fully considered, and the flexible bodies and the rigid bodies can be simulated as a whole.

Joints are added among the parts to describe fixed or rotational connections.The torque, whose value is determined by the input from the control system model created in Matlab/Simulink,is applied to the azimuthal rotational joint to simulate the drive torque from the DC motor and the reducer.A wind force is applied to the remote point of the primary reflector to simulate the wind disturbance.

To ensure that the mechanical structure model is constructed as closely as possible to the real-world structure of LCT, we read the technical manuals and research papers of LCT and consulted our Chilean colleagues who constructed the original structure model of LCT to ensure that the size,the structure and the material of each component of LCT's model are the same as the actual ones.After modeling, we also checked the parameters such as the mass, the center of mass, and the volume of each component.Then the mechanical structure model of LCT in Adams is ready for collaborative simulation.

Figure 8.The diagram of collaborative simulation of mechanical structure and control systems of LCT.

Figure 9.The diagram of LCT's control system.

3.Collaborative Simulation between Adams and Simulink

Only when the mechanical structure model of LCT, the control system model of LCT and the wind disturbance model are all accurately constructed, the servo system controller that is designed based on collaborative simulation can have similar performance as it works in a real-world system.In this section,an overview of the collaborative simulation will be introduced at first, based on which we will develop the control system model, the wind disturbance model, and the collaborative simulation system.Since the methods of controlling the telescope's elevation angle and azimuth angle are similar, for the clarity of the expression, in this section we concentrate on the control of the azimuth angle and fix the elevation angle to 45°.

3.1.Overview of the Collaborative Simulation

The control system model of LCT and Davenport's wind disturbance model is built in Simulink.The rigid-flexible coupling mechanical structure model of LCT is constructed in Adams.The collaborative simulation is implemented through the collaborative module that is generated by Adams and operated in Simulink by integrating with the control system model.The overall structure of the collaborative simulation is illustrated in Figure 8.

3.2.Modeling of LCT’s Control System

LCT's control system model is composed of the controller,the electrical subsystem of the DC motor, and the mechanical subsystem of the DC motor.Detailed description of the control system model can be found in Chen & Wang (2022).The diagram of LCT's control system is shown in Figure 9.

3.3.Modeling of the Wind Disturbance at Chajnantor Plateau

The wind disturbance model was built by using the method of Davenport spectrum(Gawronski 2008).The total wind force is a summation of the steady-state wind and the wind gust.Only the wind force acting on the primary reflector is considered in this section.The magnitude and direction of the wind force are calculated in the Simulink model and applied to the primary reflector of the mechanical structure model in Adams through the collaborative simulation module.The process of modeling the wind force is given as follows.

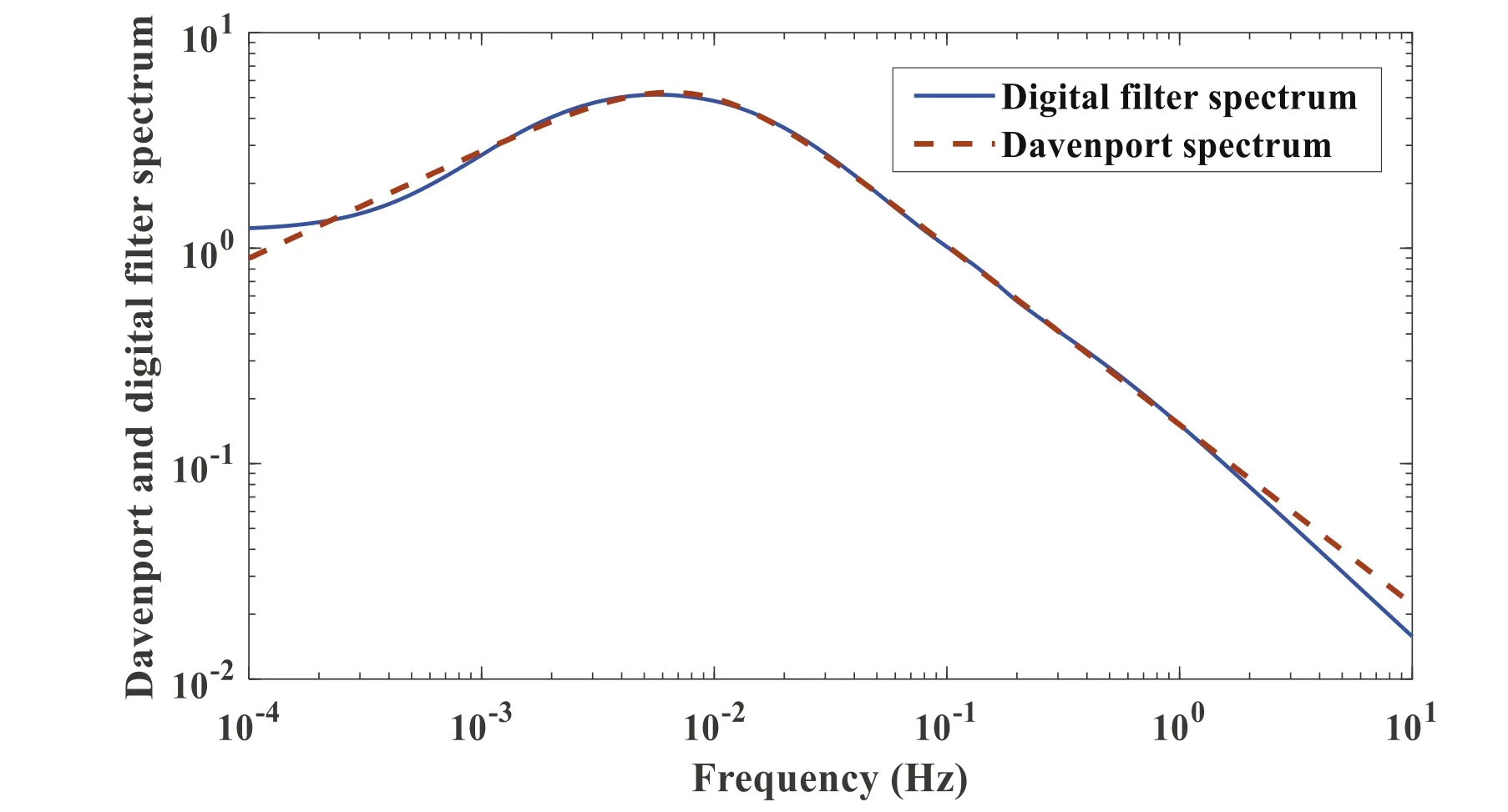
Figure 10.The fitting performance of the digital filter.

The wind velocity v is a combination of the steady-state velocity vm(i.e., the velocity of the steady wind) and the gust velocity Δv (i.e., the velocity of the wind gusts):

where vm=10 m s−1is obtained from the climate data at the new site of LCT on Chajnantor Plateau.

The energy of the wind gust Sv(ω) is determined by the frequency of the wind, which can be described by the Davenport spectrum as follows:

where z=7.12 m is the distance from the ground to the center of the primary reflector and z0=0.1 m is the height of the terrain roughness.

Since the Davenport spectrum Sv(ω) describes the relationship between the wind frequency and the energy of the wind gusts(i.e.,the frequency-domain response of the wind gusts),a digital filter will be designed for acquiring the time-domain characteristics of the wind gusts such that its frequency-domain characteristics is as close to that of the Davenport spectrum as possible.To fit the Davenport spectrum within the antenna's bandwidth of [0.001, 20] Hz, we construct a fifth-order digital filter H(s) (i.e., the Davenport filter) as follows:

To ensure that the frequency-domain characteristics of the digital filter as close to the one of the wind gusts described by the Davenport spectrum as possible.Figure 10 illustrates the Bode diagrams (i.e., frequency characteristics) of Equation (6) and Equation(8),in which the blue line represents the Bode diagram of the Davenport spectrum,and the red dashed line represents the Bode diagram of the fitted fifth-order digital filter H(s).

Then the wind gust velocity Δv can be obtained by inputting the white noise signal to the proposed digital filter H(s)(Equation (8)).According to the climate data of Chajnantor Plateau, the peak-to-valley value of the gust is about 6 m s−1.By adjusting the white noise power,the gust velocity waveform can be made similar to the real wind velocity record.The gust velocity generated by the digital filter is shown in Figure 11.

The wind force F is the summation of the steady-state wind force Fmand the gust force Fω, i.e.,

The steady-state wind force Fmis described asFm=kF vm2and kFis defined as kF=0.5r0πR2,where R=5.2 m is the radius of the primary reflector and r0=0.583 kg m−3is the density of plateau air.So kF=24.7625 N s2m−2.The wind gust force Fωis calculated as Fω=kfΔv,wherekf= 2kFαvm2andα= 6k.For the new site of LCT, we have vm=10 m s−1, k=0.0088 and kf=1137.9979 N s m−1.

Figure 11.The gust velocity generated by the digital filter with the white noise.

Figure 12.The diagram of the connection between the wind disturbance model and the collaborative simulation module.

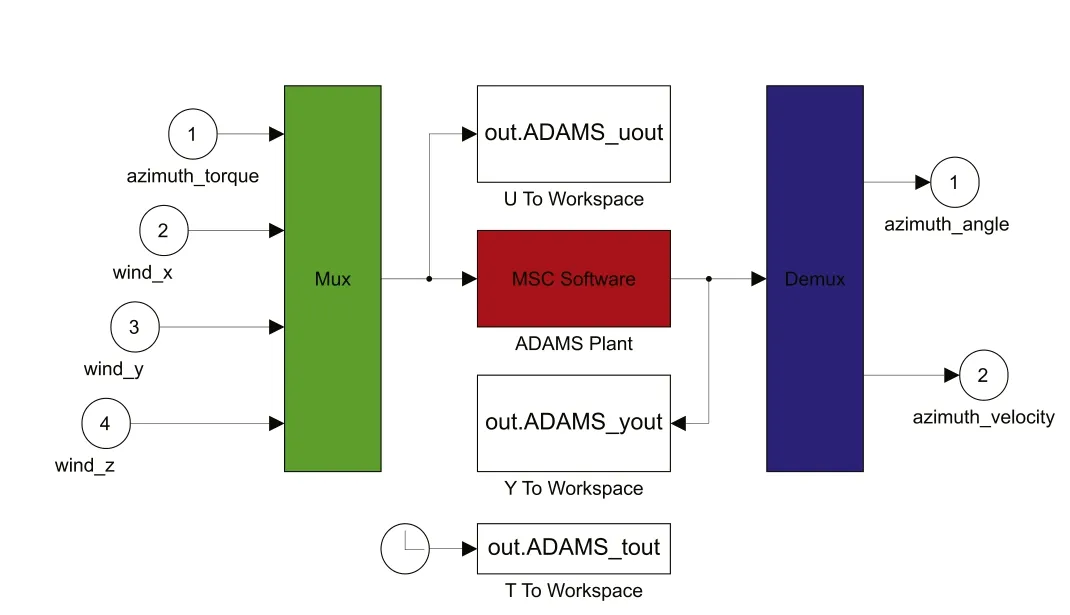
Figure 13.The “adams_sub”module for collaborative simulation.

To represent the direction of the wind force, the total wind force F is decomposed into three components, i.e., Fx, Fyand Fzin the ground coordinate of LCT.The three components are given by:

where α is the elevation angle of the wind and β is the azimuth angle of the wind in the ground coordinate of LCT.

Figure 14.The Simulink diagram of the collaborative simulation.

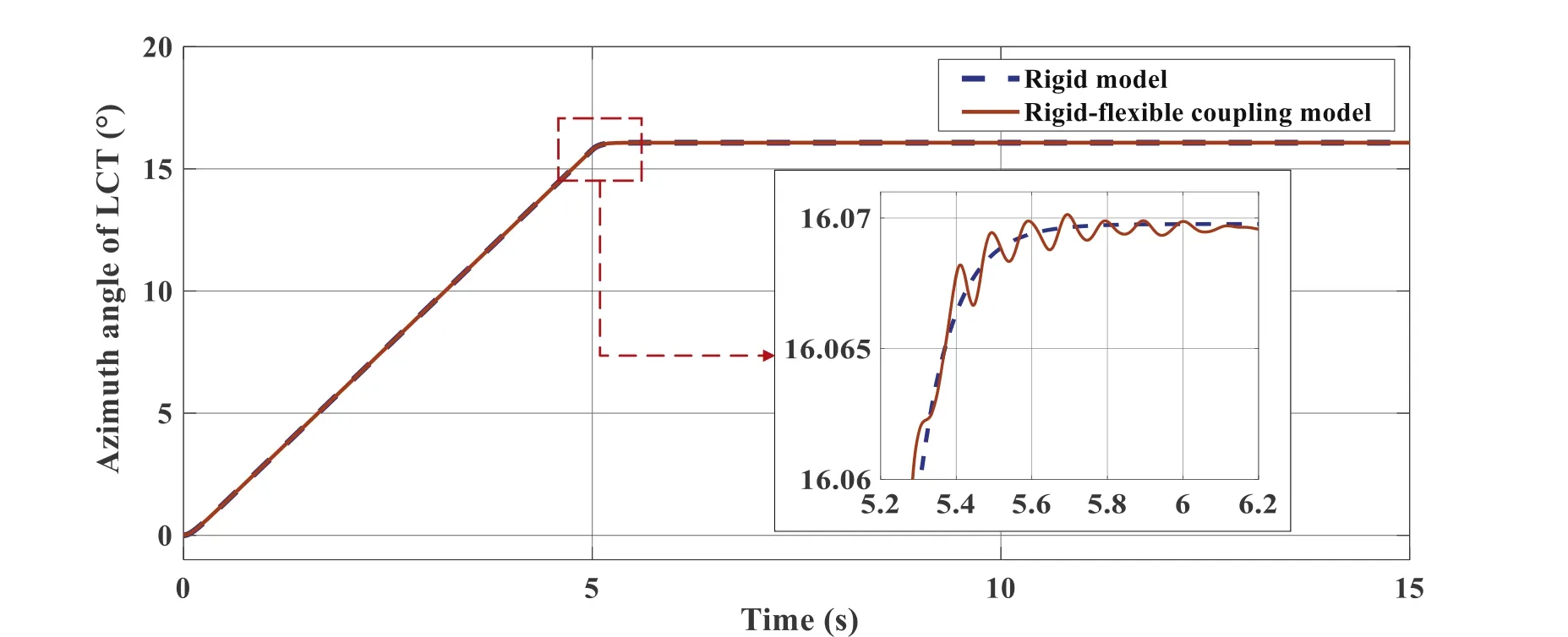
Figure 15.The azimuth angle of LCT.

The three wind force components are calculated and loaded into the collaborative simulation module for further simulation.The diagram of the connection between the wind disturbance model and the collaborative simulation module is shown in Figure 12.

3.4.Collaborative Simulation Module

The collaborative simulation based on Simulink and Adams is implemented through “adams_sub”, a Simulink module for integrating with Adams.The internal parameters of this module are exported from the mechanical structure model in Adams and imported to the MATLAB workspace.The core function of this module is to call Adams programs through an s-function and interactively simulate with the model in Adams.Before simulation, the input and output of the “adams_sub”module need to be specified.The inputs of the“adams_sub”module are the data passed from the control system model in Simulink to the mechanical structure model in Adams.The outputs of the“adams_sub”module are the data generated in the mechanical structure model in Adams and fed back to control system model in Simulink.Figure 13 shows the structure of the“adams_sub”module for collaborative simulation.

The input variables represent the forces or moments applied in Adams model.Specifically in the collaborative simulation of LCT, “AZIMUTH_TORQUE”represents the torque acting on the azimuth axis and “WIND_X”, “WIND_Y”and “WIND_Z”represent the wind force acting on the primary reflector.The wind force is decomposed into three directional components according to the ground coordinate system.The wind direction and magnitude can be freely specified based on the input of the winds in the three directions.The output variables are azimuthal angle and azimuthal velocity, which are measured at the point where the drive torque is applied.The azimuth angle is in degree and is mainly used for the angle feedback of the controller.The azimuthal velocity is in degree per second(°s−1)and is mainly used to simulate the rotational friction of LCT.

Figure 16.The azimuth velocity of LCT.

Figure 17.The performance of the azimuth control.

The Simulink diagram of the entire collaborative simulation is shown in Figure 14.

4.Results and Discussion

4.1.Mechanical Structure Model

A comparison experiment of the mechanical structure models is conducted to verify the flexibility of the rigidflexible coupling model of LCT constructed in this paper.The same torque is applied to the azimuth axis of the rigid-flexible coupling model and the rigid body model and their responses to the torque are observed and compared.The input torque is applied with value of 100,000 N m at the beginning of simulation (i.e., 0 s) and is removed at the 5th second.The rigid-flexible coupling model is tested in Simulink through the collaborative simulation module.The rigid body model being compared is the one used by Chen & Wang (2022) for designing the position controller of LCT, in which the telescope is simplified as a rigid body with a transfer function considering only the rotational inertia with the value of 160,560 kg m2.Output angles and angular velocities of the two models are observed for comparison.The wind disturbance is not considered in this experiment.The output angles are shown in Figure 15 and the angular velocities are shown in Figure 16.

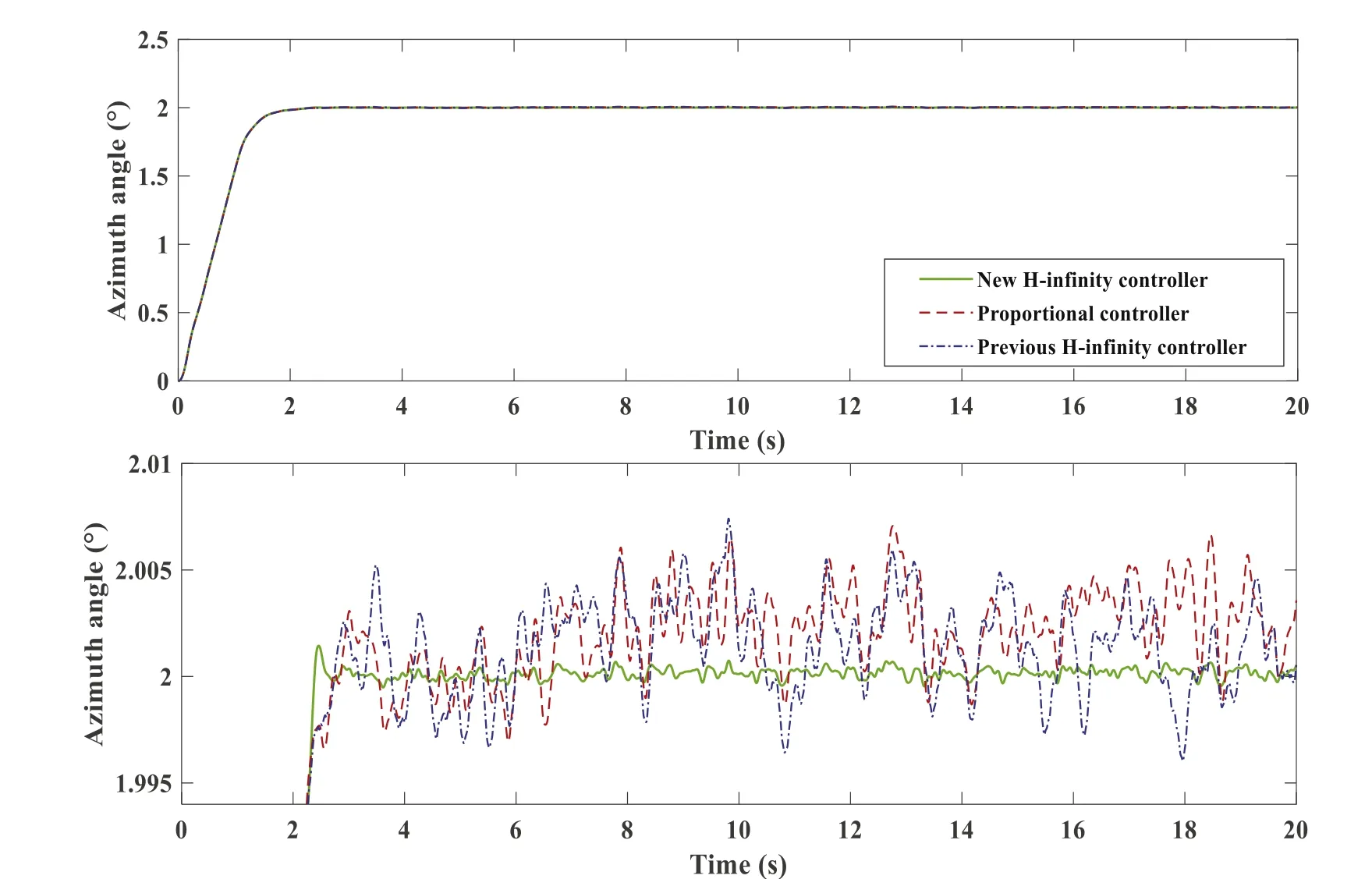
Figure 18.The control performance of the new H∞controller, the proportional controller and the previous H∞controller.

Table 4 Mean and RMSE of Azimuth Angle

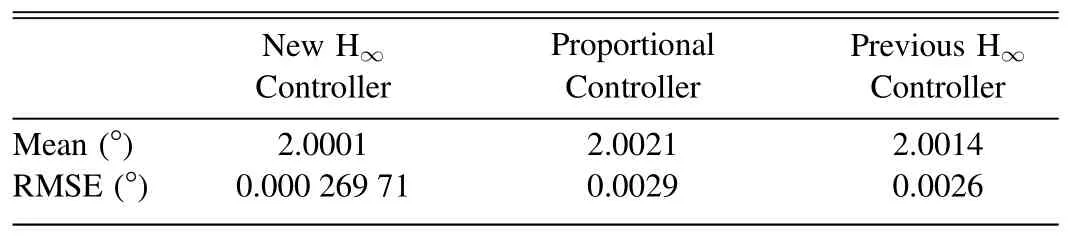
Table 5 Mean and RMSE of Azimuth Angle Based on Three Controllers

The coincidence of the values and trends of the two models shows that the rotational inertia of the rigid-flexible coupling model is accurate.From the fluctuation of the angle and angular velocity around the time epoch (i.e., the 5th s) when the value of the input torque changes suddenly, the rigid-flexible coupling model depicts the flexible characteristics of LCT,which cannot be depicted by the rigid model.

4.2.Control Performance Under Wind Disturbance

As shown in the previous subsection, the vibrations of LCT in a real control system can be simulated by the collaborative simulation method.In this section, the influence of these vibrations on the azimuth control will be investigated through comparative experiment.The azimuth angle of LCT is initially 0°and the target angle is 5°.The proportional control policy is employed.The servo system is described in Subsection 3.2 and the wind disturbance model is built in Subsection 3.3.The collaborative simulation module representing the rigid-flexible coupling LCT model and the transfer function module representing the rigid model are compared.The performance of the azimuth control is shown in Figure 17.

From Figure 17, under wind disturbance, the azimuth angle of the rigid-flexible coupling model fluctuates more than that of the rigid model.The mean and the root mean square error(RMSE)of the azimuth angle after the 3rd s for the rigid model and the rigid-flexible coupling model are given in Table 4.From Table 4,the RMSE of the rigid-flexible coupling model is greater than the RMSE of the rigid body model by 26%.The simplified way of ignoring the flexibility of LCT hides part of the disturbance influences, which may cause the designed controller fails to perform as expected in the real telescope.

4.3.Performance of the New H∞Controller Based on the Collaborative Simulation

The H∞controller (Gawronski 2001) is capable of suppressing the disturbances added to the controlled system and has good robustness.Although the H∞controller is not model-free,it does not depend on the accuracy of the model of the controlled system very much and good control performance can be achieved by adjusting a few parameters in the case that the model of the controlled system is modified partly but not significantly.Based on the above advantages,the H∞controller has been applied to the anti-disturbance servo control of some radio telescopes.

An H∞controller was designed for anti-disturbance control of the simplified model (the rigid body model).Compared to the proportional controller,it can suppress the wind disturbance and reduce the steady-state error.However, the control performance is not good when the H∞controller is applied to the rigid-flexible coupling model.The reason is that the H∞control policy is model-based one and the control parameters designed based on the rigid model are not suitable for the rigidflexible coupling model.In addition, the increased fluctuations due to flexibility are beyond expectation.The parameters of the H∞controller is retuned based on the rigid-flexible coupling model.A comparison of the control performance of the new H∞controller,the proportional controller and the previous H∞controller based on the rigid-flexible coupling model is shown in Figure 18.The proportional controller,which has been used by the CSO telescope (which is the former name of LCT) and been working well since 1980s,is selected as the control group for the two H∞controllers.The conditions of the comparison experiment are the same as in Subsection 4.2.

The mean and the root mean square error (RMSE) of the azimuth angle after the 3rd s under the three types of controllers are given in Table 5.From Figure 18 and Table 5,the previous H∞controller has no significant improvement on control performance compared to the proportional controller.The new H∞controller not only greatly reduces the steady-state error,but also significantly suppresses the disturbances.The importance of using the collaborative simulation method to build a more accurate model for controller design is demonstrated.

5.Conclusion

LCT will be relocated and refurbished at the new site.The new servo controller of LCT requires better control performance and the ability of suppressing large wind disturbances.In the previous research on designing the controller for LCT,the telescope is simplified as a rigid body and the effect of structural flexibility is ignored, which would affect the performance of the controller when it is employed in the real telescope.In this paper,a rigid-flexible coupling model of LCT is constructed based on the available design documents of LCT.Then the simulation model of LCT's control system is introduced.A Davenport wind disturbance model is established based on LCT's structure and the climate on Chajnantor Plateau.Based on Adams and Simulink, a collaborative simulation model is developed, which integrates the mechanical structure model with the control system model.Using the constructed collaborative simulation model, some experiments are conducted.Through the comparison experiment, the rigidflexible coupling model exhibits flexible characteristics that cannot be depicted by the rigid body model.From the comparison experiment of the performances under wind disturbance,it is found that the flexible characteristics increase the effects of wind disturbance on the control system, which increases the difficulty of control.Finally, by comparing the performance of the three controllers, the previously designed controller based on the rigid-body model does not perform well when applied to the more realistic rigid-flexible coupling model.By readjusting the parameters according to the rigidflexible coupling model, the new controller greatly reduces the steady-state error and suppresses the disturbances.The results prove that building a collaborative simulation model that connects the control system with the more realistic rigidflexible coupling model is valuable for the design and optimization of the new LCT controller.

Acknowledgments

We would like to thank our Chilean colleagues (i.e., J.T.Vial, D.Arroyo, C.Canales, J.Navarro, E.Dufeu, R.Reeves,and N.Lastra from Universidad de Concepción, Chile) of the Leighton Chajnantor Telescope (LCT) Project for their efforts on developing the original SolidWorks model of LCT, based on which we reconstructed the mechanical structure model of LCT in Ansys and Adams.

ORCID iDs

Wei-Rui Chen https://orcid.org/0000-0003-2603-6338