基于离散元法的砾岩水力压裂裂缝扩展规律及主控因素

2023-05-29张家伟刘向君梁利喜

大庆石油地质与开发 2023年3期

张家伟刘向君熊健梁利喜张文张旭

（1. 西南石油大学石油与天然气工程学院，四川成都 610500；2. 油气藏地质及开发工程国家重点实验室，四川成都 610500；3. 西气东输苏北输气分公司，江苏南通 226363）

0 引言

随着中国经济和工业化不断快速发展，对化石能源的消耗需求不断增加。研究表明，中国常规油气资源量未来即将接近峰值[1‐2］，将难以满足中国发展日益增长的能源需求。随着北美页岩气的成功开发，非常规油气资源已经成为油气勘探开发的重要领域[3‐4］，非常规油气越来越受到重视。砾岩致密油是非常规油气资源的重要组成部分[5］，2018年在新疆油田玛湖凹陷发现了世界上最大的砾岩油田，被证实探明石油地质储量达到了5.2×108t[6］，砾岩致密油资源的勘探开发对于缓解中国能源紧张的局面具有十分重要的意义。

砾岩储层普遍具有低孔、低渗的特点，自然产能较低，需要进行压裂改造才能实现大规模投产开发[7‐11］。在压裂施工改造过程中，评价压裂效果最主要的判断指标就是压裂缝的几何形态。近年来，国内外学者在水力压裂裂缝延伸的规律和机制上进行了大量的理论、物理实验和数值模拟研究。在理论研究方面，国外有些学者提出了裂缝在材料中的起裂和扩展机理[12‐14］，国内张广清等[15］利用拉格朗日法和最大拉应力准则建立了水力裂缝空间模型，H.Y.Tang 等[16］基于DDM 方法提出多平面压裂缝扩展模型，J.N.Dong 等[17］解释了流体与裂缝尖端的动态关系。在物理实验方面，刘鹏等[18‐21］通过真三轴水力压裂模拟系统研究了不同应力比和粒径比、注入速率、水平井角度和砾石粒径等因素对裂缝扩展的影响。在数值模拟方面，李连崇等[22‐23］通过有限元RFPA 模拟砾岩地层裂缝扩展过程并发现了5 种裂缝的扩展形态，X.Shi 等[24］采用CZM 模拟了含裂缝的强非均质性砾岩水力压裂裂缝扩展路径。

尽管已经取得了许多对砾岩储层油气勘探开发具有指导意义的研究成果，但有限元法和物理实验同样具有较大的局限性，前者具有网格不能实时更新、裂缝尖端网格划分困难以及高密度网格牺牲大量的算力等局限性，后者存在难以大规模开展实验，难以充分认识砾岩储层中裂缝扩展规律和量化相关研究等问题。离散元法在研究非连续介质力学问题上具有显著的优势，能够实时计算跟踪颗粒之间的交互作用，精确揭示微观尺度上的力学响应，能够捕捉裂缝成核、起裂延伸，并能描述复杂的裂缝形态，因此在岩石水力压裂领域得到大量应用。

本文采用离散元方法，基于渗流−离散元耦合模型建立砾岩水力压裂模型，研究砾岩储层地质因素（砾石粒径、胶结强度、砾石强度）以及工程因素（地应力）对水力裂缝扩展规律的影响。利用随机森林分析各因素对水力压裂效果影响的重要程度，并采用层次分析法构建储层压裂计算模型。研究结果对认识砾岩储层水力裂缝的扩展机理及压裂选层可提供一定参考。

1 砾岩离散元模型

1.1 离散元法

本文在离散元模拟软件PFC2D平台上进行建模、模拟。在离散元法中采用颗粒表示岩石的矿物组分，采用键表征岩石矿物颗粒间的黏结特性，用平行黏结模型表示（图1），可以很好地模拟岩石的力学行为。

图1 平行黏结模型Fig. 1 parallel bond model

平行黏结模型可用于模拟材料的拉张破坏特性，也能模拟材料的剪切破坏特性，其构模型表达式为

式中：——黏结键周边法向应力，MPa；n——黏结键接触处的法向力，kN/m；b——接触点的弯矩，kN/m；——两颗粒的平均半径，m；——横截面面积，m2；——惯性矩，m4；——力矩贡献系数。

离散元法能准确地表征材料微观力学性质，根据颗粒之间的黏结即可判断是否产生裂缝及裂缝的位置。当颗粒间的拉张应力超过拉张强度时，颗粒间的法向黏结破坏，从而形成张性裂缝；当颗粒间的切应力超过剪切强度时，颗粒间切向黏结被破坏形成剪切裂缝。当外部载荷持续增加，黏结键持续断裂，裂缝持续增加，在模型上显示出累计裂纹，起裂准则关系式为：

式中：σt——拉张应力，Pa；τ——切应力，Pa；σn——法向压应力，Pa；Fs——法向切向力，Pa；φ——内摩擦角，（°）。

1.2 砾岩单轴模型及其参数

砾岩取自于玛湖凹陷百口泉组，埋藏深度3 109~3 259 m，砾石体积分数30%~70%，粒径5~70 mm。砾岩储层孔隙度为2.1%~6.4%，渗透率0.126×10−3~0.613×10−3μm2，具有低孔、低渗的特点。通过CAD 软件获取砾石轮廓后，导入到离散元模型中，数值模型由砾石、基质和胶结界面构成，模型长×宽尺寸为100 mm×100 mm，见图2。

图2 砾岩离散元模型Fig. 2 Discrete element model of conglomerate

由于离散元数值模型中颗粒的细观力学参数与材料的宏观力学参数之间没有严格的对应关系，因此多采用“试错法”标定细观力学参数，直到模型符合宏观力学行为[25］。砾石与基质之间主要为泥质胶结，强度由高至低依次为砾石、基质、胶结，为降低问题的复杂性，本文对砾石统一赋值。“试错法”标定结果表明（图3），数值模拟与室内实验的应力−应变曲线在峰值强度前及峰值强度点吻合度较好，弹性模量误差为1.9%，峰值强度误差为1.6%，均在合理误差范围内（图3（a））。数值模拟结果的破坏形态与室内实验结果一致（图3（b）），也表明了细观参数的合理性。

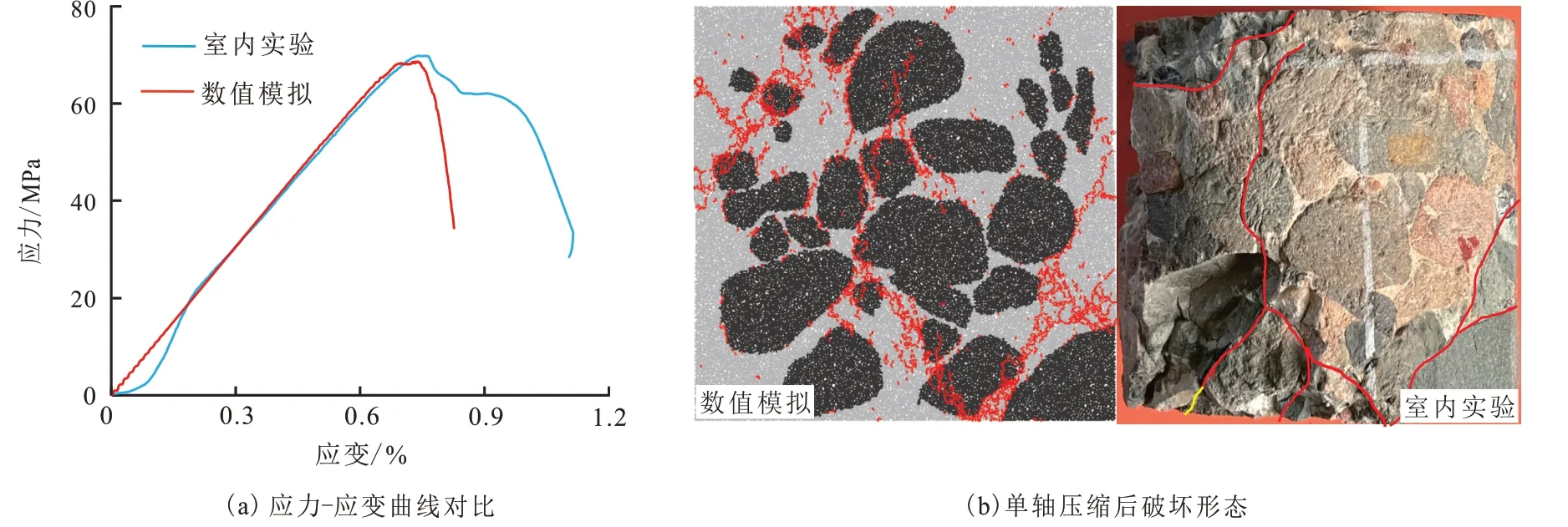
图3 “试错法”标定的数值模拟与室内实验结果Fig. 3 Results of numerical simulation calibrated by trial⁃and⁃error method and lab experiment

1.3 水力压裂模型

根据真实砾岩样品的砾石分布情况，建立了细砾岩、中砾岩和粗砾岩的砾岩数值模型，砾石平均直径分别为5、25 和60 mm。模型为边长100 mm的正方形，模型的边界为无流动边界，4 个可以移动的边界将被用于围压伺服的模拟，如图4 所示。数值模型由11 806 个颗粒组成，细观力学参数由单轴实验标定（表1）。

表1 数值模型细观参数Table 1 Meso-parameters of numerical model

图4 基于真实砾岩结构的水力压裂模型Fig. 4 Hydraulic fracturing model based on real conglomerate structure

1.4 模型准确性验证

为了验证数值模拟结果的准确性，用参考文献[26］给出的实验结果进行比较。数值模型的最大水平主应力σmax与最小水平主应力σmin分别为9 和3 MPa，与参考文献保持一致。

图5 为砾岩样品室内实验和数值模拟压裂后裂缝的扩展形态对比，数值模拟压裂过程中裂缝在砾岩中的表现有4 种类型：止砾、绕砾、嵌入穿砾直至整体失稳破坏，数值模型的结果与物理实验基本一致。数值模型中裂缝的扩展受到裂缝与砾石之间相互作用影响进而影响裂缝扩展路径。水力压裂能量的增加可以保证裂缝扩展遵循最大主应力方向，但是局部应力集中导致裂缝在砾石周围扩展，在大多数情况下砾石具有较高的力学强度导致穿砾现象较少。因此砾岩储层在水力压裂时，常常出现砾石吸引裂缝现象。模拟结果显示，在砾岩压裂过程中裂缝主要沿水平最大主应力方向扩展（图5（a）），并且在最大主应力方向上基质与砾石的胶结面扩展，可以明显的看出裂缝存在绕砾与吸引的现象（图5（b））。模拟结果与参考文献[26］中物理实验结果基本一致。

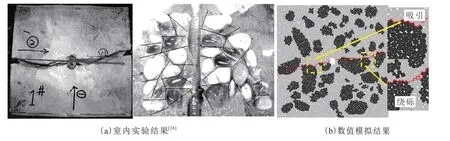
图5 水力压裂室内实验与离散元数值模拟结果对比Fig. 5 Comparison between hydraulic fracturing laboratory experiment and discrete element numerical simulation results

2 水力压裂数值模拟

2.1 砾石强度对裂缝扩展的影响

对细、中、粗3 种不同砾岩开展压入硬度测试，测试结果分别为395、844 和635 MPa，表明同一砾岩的砾石力学特性也存在较大差异。为了研究砾石强度对裂缝扩展的影响，保持基质强度不变，改变砾石强度，使砾石强度比（砾石强度与基质强度的比值）分别为1.0、1.5、2.0、2.5 和3.0。压裂破坏后的数值模型（图6（a））表明，水力裂缝沿最大主应力方向延伸形成双翼缝。在低砾石强度比情况下，裂缝容易发生穿砾行为；当砾石强度比较高时，绕砾现象增加，尤其在细砾岩与中砾岩中最为常见，发生这种现象与这两种砾岩中砾石密度分布较高有关。裂缝在最大主应力方向延伸时，砾石强度比越高，裂缝向前扩展难度越大，导致地层的破裂压力增加（图6（b））。因此，对于破裂压力高低而言，本质上是由于砾石对裂缝的阻碍作用提高了裂缝扩展所需要的能量。

图6 不同砾石强度比条件下的数值模型、破裂压力和各区域裂缝分布Fig. 6 Numerical model, fracture pressure and fracture distribution in each area under different gravel strength ratios

为了研究压裂缝发生绕砾的临界条件，通过提取基质、砾石和胶结面中裂缝的数量，得到了基质、砾石和胶结面不同区域裂缝数占总裂缝数比例的分布情况（图6（c）），以此表征出不同情况下裂缝的主要扩展区域。以中砾岩为例，随着砾石强度比的增加，胶结区域裂缝数所占比例先增大后稳定，而砾石和基质区域的裂缝数所占比例则先减小后稳定。胶结区域裂缝数所占比例的增大，表明裂缝发生了较多的绕砾行为，而胶结区域裂缝数所占比例保持稳定则表明了裂缝绕砾行为趋于稳定。因此，在当前模拟条件下，当砾石强度比为2.0 时，水力裂缝将由穿砾完全转变为绕砾。对于砾岩储层，不仅要充分认识砾岩整体的力学性能，还要对砾石粒径、砾石强度特征进行充分研究，以便制定出有针对性的压裂改造措施。

2.2 胶结强度对裂缝扩展的影响

胶结强度也是影响砾岩储层裂缝扩展规律的重要因素。因此固定基质和砾石强度，改变胶结强度，使胶结强度比（胶结强度与基质强度的比值）分别为0.1、0.3、0.5、0.7 和0.9。不同胶结强度比条件下水力压裂破坏后模型裂缝扩展情况如图7（a）所示，当胶结强度比较低时，井筒附近砾石受到注水压力的影响产生应力扰动，在井眼附近的胶结处产生微裂缝。砾石粒径越大，越容易在井眼附近区域发生胶结破坏。随着胶结强度比的增加，裂缝由向井筒周围多个方向扩展多条压裂缝转变为沿着水平最大主应力方向扩展的两翼缝。此外，胶结强度比越高，地层破裂压力也越高（图7（b））。

图7 不同胶结强度比条件下的数值模型、破裂压力和各区域裂缝分布Fig. 7 Numerical model, fracture pressure and fracture distribution in each area with different cementing strength ratios

由于在研究砾石强度和胶结强度对裂缝扩展行为的影响时均采用了统一的基质强度，胶结强度比从0.1 增加到0.9 时，地层破裂压力增加了5.55 MPa，而砾石强度比从1.0 增加到3.0 时，地层破裂压力增加了1.4 MPa，从单位强度变化对地层破裂压力的影响看，胶结强度对地层破裂压力的影响更加显著。

按照相同的方式分析不同胶结强度比影响下的裂缝绕砾临界情况，基质、砾石和胶结面各区域裂缝数量占裂缝总数的比例分布如图7（c）所示。当胶结强度比从0.1 增加至0.5 时，胶结区域裂缝数所占比例快速减小，而基质和砾石区域的裂缝数所占比例出现增大，当胶结强度比大于0.5 时，胶结区域裂缝数所占比例趋于稳定。因此，当胶结强度约为基质强度的一半时，是裂缝绕砾与穿砾行为的临界值。但这并不代表在压裂过程中需要尽可能选择低胶结强度的砾岩储层，如果胶结强度过低，如胶结强度比为0.1 情况下，大量裂缝形成于砾石与基质交界处，导致岩体结构失去稳定性，在后续开发中容易出现出砂等复杂工况。因此砾岩储层制定压裂施工方案时应选择砾石粒径较小、具有一定胶结强度的地层，既保证了裂缝网络的建造质量，又有利于延长油井的生产时间。

2.3 水平应力差对裂缝扩展的影响

为了研究水平应力差Δσ（最大水平主应力σmax与最小水平主应力σmin之间的差值）对裂缝扩展的影响，建立了5 种不同水平应力差边界条件，见表2。

表2 数值模型水平应力及应力差Table 2 Horizontal principal stress and stress difference of numerical model MPa

图8（a）为不同应力差条件下破坏后模型的裂缝扩展形态。从图8（a）可以看出，水平应力差对裂缝扩展的影响显著，在水平应力差为1 MPa时，地应力对裂缝的影响最弱，模型在井筒周围形成了3 条主裂缝，由于砾石的存在使裂缝发生转向。随着水平应力差的增加，地应力对水力裂缝的影响逐渐增大，水力裂缝开始逐渐向最大水平主应力方向扩展，在井筒周围产生2 条主裂缝，非最大水平主应力方向的裂缝逐渐消失。

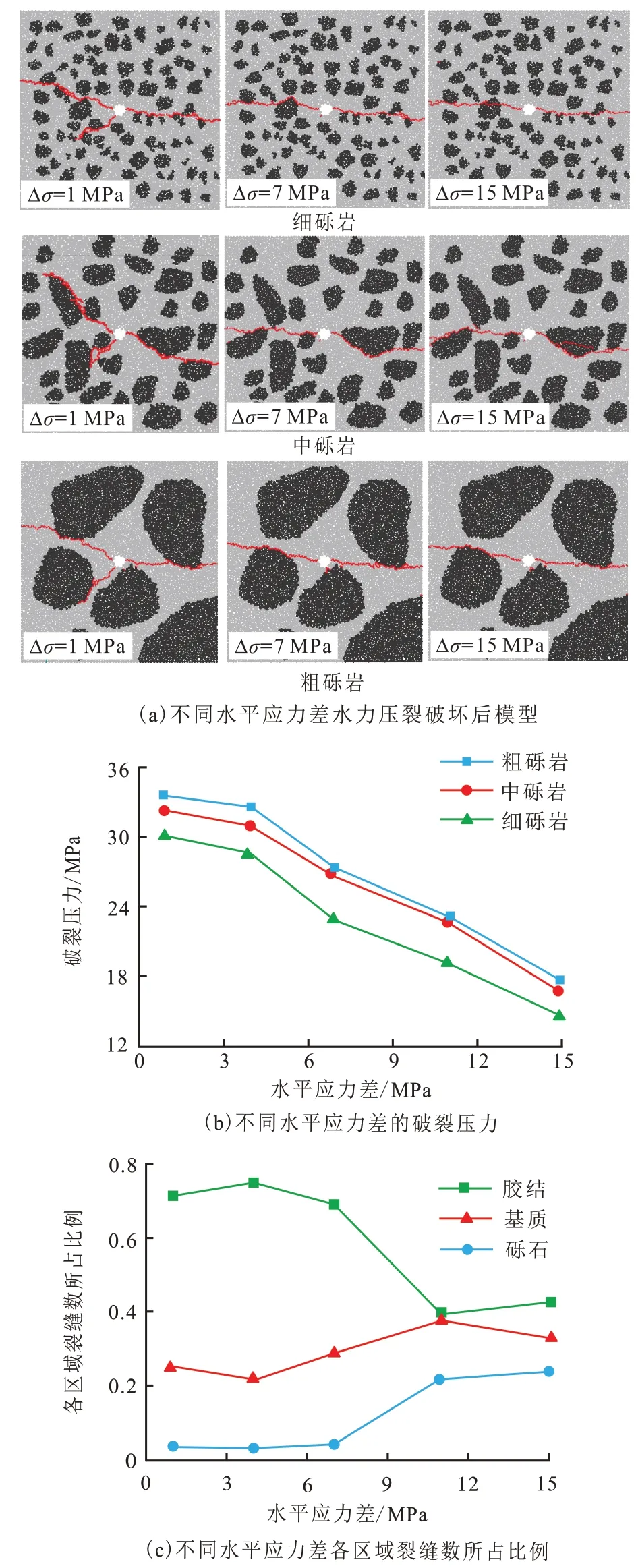
图8 不同水平应力差条件下的数值模型、破裂压力和各区域裂缝分布Fig. 8 Numerical model, fracture pressure, and fracture distribution in each area with different horizontal stress differences

图 9 不同无因次裂缝长和无因次破裂压力条件下的储层可压裂指数Fig. 9 Reservoir fractability index with different dimensionless fracture lengths and dimensionless fracture pressures

从不同水平应力差条件下的破裂压力变化情况来看图8（b），破裂压力与水平应力差呈负相关性，主要原因是裂缝在沿着最大水平主应力方向扩展过程中，裂缝一方面需要克服岩石颗粒与颗粒之间的黏结强度，另一方面需要克服最小水平主应力的影响，表现出破裂压力随水平主应力的减小而增加的现象。

不同区域裂缝数占总裂缝数的比例随应力差的变化表现为3 个阶段（图8（c））。在第1 个阶段，当应力差低于7 MPa 时，分布在砾石、基质和胶结区域的裂缝数量所占比例相对稳定，说明裂缝形态没有发生较大的变化；在第2 个阶段，当应力差大于7 MPa 但小于11 MPa 时，胶结区域的裂缝数所占比例逐渐减小，砾石区域的裂缝所占比例稳定增加，表明绕砾行为减少，穿砾行为增加；在第3 个阶段，当应力差增大到15 MPa 时，对于一般地层来说，应力差相当大，裂缝传播方向稳定，形态单一，不利于形成复杂的缝网。

3 主控因素及压裂改造效果

韩珊等[27‐28］利用随机森林定量分析了压裂产能的主控因素，得出了压裂改造中各因素对油气产能的重要程度。本文利用离散元数值模拟结果，基于随机森林算法以胶结强度比、粒径、砾石强度、水平应力差等变量作为因素，以数值模型中的压裂后无因次裂缝长为目标变量，计算出各个因素对目标变量的重要程度（表3）。计算结果表明，胶结强度比和水平应力差对压裂缝长的重要程度较高而砾石粒径和砾石强度比对压裂缝长的影响相对较小。

表3 各因素与压裂缝长关联度Table 3 Correlation between various factors and hydraulic fracture length

在分析各因素对压裂效果影响的基础上，利用层次分析法确定胶结强度比、水平应力差和砾石粒径3 个因素的权重，从而对储层可压裂性作出评价。采用层次分析法对可压裂效果的影响因素进行正向或负向归一化处理，使之所有影响因素与压裂缝长呈正相关，即经归一化处理后的因素越大，压裂缝延伸越长。在归一化处理的基础上通过两两因素对比衡量各因素的权重，采用1—9 和其对应的倒数作为各因素的权重[29‐30］，建立层次分析矩阵，构建出可压裂性指数判断矩阵（表4）。在此基础上利用层次分析理论中的特征向量法计算出各因素权重，胶结强度比、水平应力差和砾石粒径的权重分别为0.493、0.311、0.196。

表4 储层可压裂性判断矩阵Table 4 Reservoir fracability determination matrix

基于层次分析法考虑胶结强度比、水平应力差和砾石粒径等因素的影响，储层可压裂性指数计算模型为

式中：FI——储层可压裂指数；σce——归一化胶结强度；Δσg——归一化水平应力差；d——归一化砾石粒径。

基于离散元模拟结果，根据建立的可压裂性指数计算模型，储层可压裂性指数与无因次裂缝长存在较好的相关性（图9（a））。同时，可压裂性指数与无因次破裂压力也存在较好的相关性（图9（b））。即可压裂性指数越高，岩石越容易破裂，说明所构建的权重系数具有一定的可靠性。

在以上研究的基础上，通过研究区已压裂试油资料进一步分析储层可压裂性的影响因素。比采油指数是单位压差下每米地层的产量，能较好地表征单井储层物性和压裂改造的效果。

研究区某井的比采油指数与水平应力差和单轴抗压强度关系如图10 所示。由图10（a）可以看出，比采油指数呈现出随着水平应力差的增大而减小的变化趋势，表明在相对较低比采油指数情况下，储层自身的渗透性能低，其渗透性主要是依靠于压裂改造形成裂缝。因此，低比采油指数下，适合在低水平应力差的地层进行压裂改造，从而提高储层的渗透性。

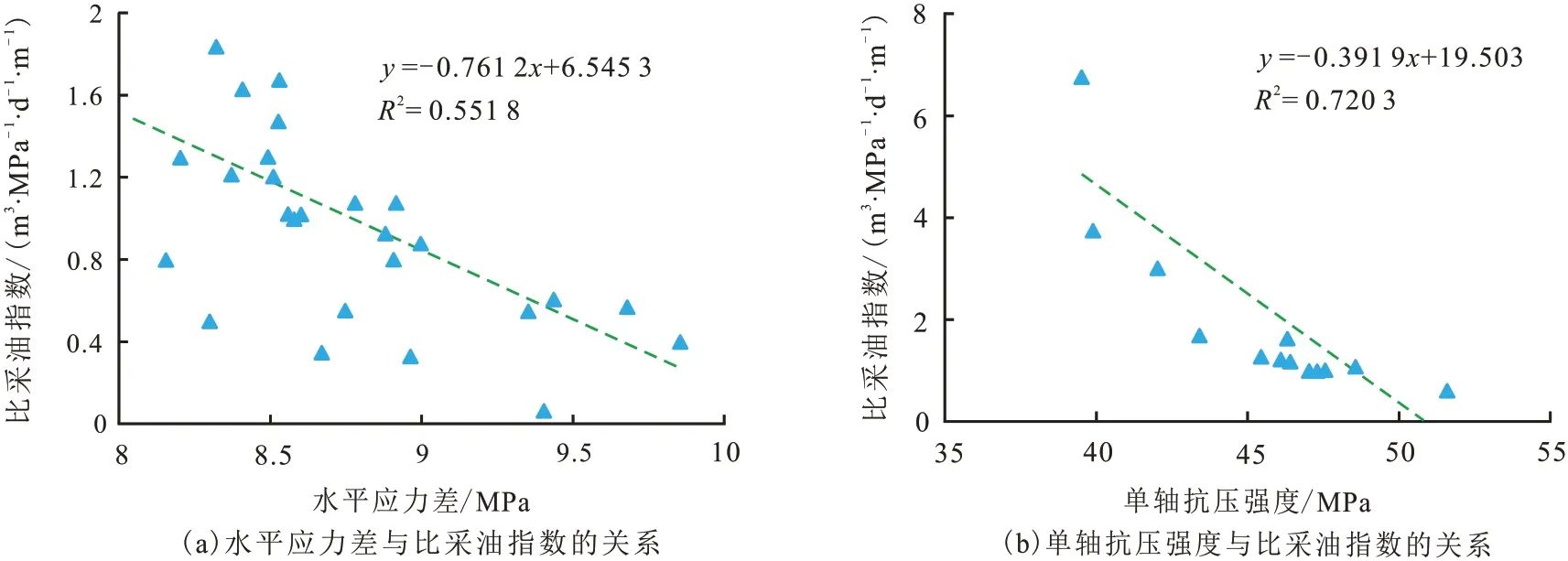
图10 不同水平应力差和单轴抗压强度条件下的比采油指数Fig. 10 Specific productivity index with different horizontal stress difference and uniaxial compressive strength

从图10（b）可以看出，随着储层砾岩单轴抗压强度的增加，比采油指数随之减小，S.Luo 等[31］研究发现砾岩胶结强度与单轴抗压强度呈正相关关系。结合压裂模型可知，砾岩储层的胶结强度较低时，容易形成复杂缝网，有利于提高压裂后产能。因此，在制定具体压裂施工方案时，应充分考虑砾岩储层地应力特征及力学特性，制定合适的压裂方案，以达到提高采收率、降低开采成本的目的。