一种无依托瞄准的角度解算方法

李发动宋小艳高明杰陈 为

(北京航天发射技术研究所,北京 100076)

1 引言

某火箭发射系统的瞄准设备采用激光捷联惯组与光学准直测量相结合的无依托瞄准方式,利用激光捷联惯组实现惯组自主定向测量,通过自准直光管完成与箭上目标棱镜的准直偏差角测量[1],最终实现箭上目标棱镜的方位角Am的测量。瞄准设备主要由激光捷联惯组和自准直光管等组成,自准直光管固连在激光捷联惯组本体上,一同安装在发射平台侧面的设备舱内,实现与箭上目标棱镜的水平瞄准,如图1 所示。

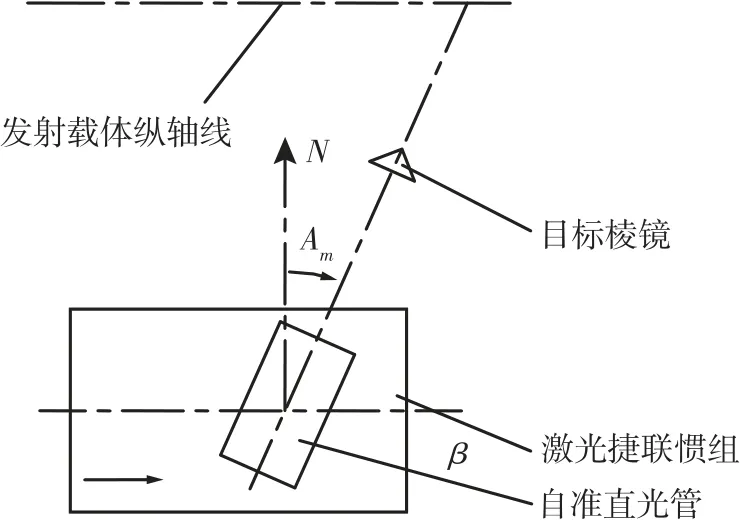
图1 瞄准设备位置关系图Fig.1 Aiming device position diagram

工作时,激光捷联惯组实现惯组自主定向测量,确定惯组载体相对地理坐标系的姿态角度,对准完成后,输出航向角ψ、俯仰角θ和横滚角γ[2],同时自准直光管完成对箭上目标棱镜的准直偏差角β的测量。但是,惯组定向测量单元和光管准直偏差角测量单元是在不同的测量坐标系下完成的,二者可能存在较大的初始安装误差,若直接对测量结果进行合成计算,则会带来较大的方位耦合误差。实际应用时,发射载体纵轴不水平度为3°,横轴不水平度为1°,自准直光管与激光捷联惯组的方位安装夹角为34°,俯仰安装夹角为0.5°,横滚安装夹角为0.1°,其耦合误差将超过1′[3]。这样的系统误差对瞄准精度来说是不可承受的,必须对耦合误差进行修正。

所给出的这种惯组瞄准下的瞄准角度解算方法,目的是将测量值转换到统一的地理坐标系下进行瞄准方位角度的合成和计算。通过矩阵方式对测量坐标系进行变换,获得输出基准在地理坐标系下的姿态角度,结合目标棱镜相对输出基准的方位偏差角度,得到所需目标棱镜的方位角度。

2 坐标系定义及变换

2.1 坐标系定义

惯组瞄准过程中使用的坐标系有地理坐标系（n系）、惯组坐标系（b系）和光管坐标系（t系）,三个坐标系的空间位置关系如图2 所示。

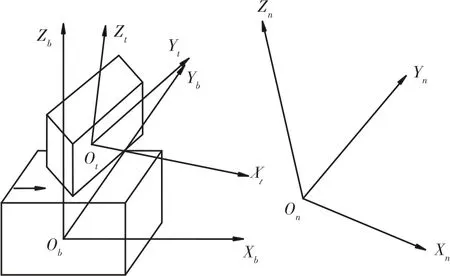
图2 坐标系空间示意图Fig.2 Coordinatesystem space schematic diagram

对三个坐标系的坐标轴做如下定义:

（1）地理坐标系（n系）

地理坐标系OnXnYnZn原点位于运载体所在的地球表面,其中一轴与地理垂线重合的右手直角坐标系。OnXn轴指向东,即E;On Yn轴指向北,即N;OnZn轴沿地垂线指向天顶,即U。这个坐标系通常叫作东北天（ENU）坐标系。惯组测量过程中涉及到的导航坐标系与地理坐标系一致。

（2）惯组坐标系（b系）

惯组坐标系Ob Xb Yb Zb的原点是惯组载体重心Ob,Ob Xb沿惯组纵轴指向右,Ob Yb沿惯组横轴方向指向前,Ob Zb沿惯组竖轴方向向上,坐标系构成右手直角坐标系。

（3）光管坐标系（t系）

光管坐标系OtXtYtZt的原点在自准直光管中心Ot,OtYt轴为光轴方向,Ot Xt Zt平面与Ot Yt轴垂直,OtXt轴垂直光管光轴指向右（与准直分划板横丝一致）,坐标系构成右手直角坐标系。

2.2 坐标系变换

坐标系变换可实现空间三维坐标点在不同坐标系下的数值转换,得到相同点在不同坐标系下的坐标值。坐标变换的目的是将不同坐标系下的角度测量值统一到相同的坐标系下,方便对测量值进行分析和计算。对于任意两个空间坐标系,可通过一次平移和三次旋转实现坐标系重合,三次旋转可以用数学方法表述成三个独立的方向余弦矩阵,以下只讨论惯组瞄准过程中涉及到的旋转关系。

2.2.1 b 系与n 系间的变换

b系相对n系的角位置可以用惯组输出的航向角ψ、俯仰角θ和横滚角γ表示,规定两个坐标系之间通过以下旋转变换关系得到重合:

其变换表达式为[4]

从b系到n系的变换按公式（2）计算。

2.2.2 t 系与b 系间的变换

t系和b系的位置关系如图3 所示。

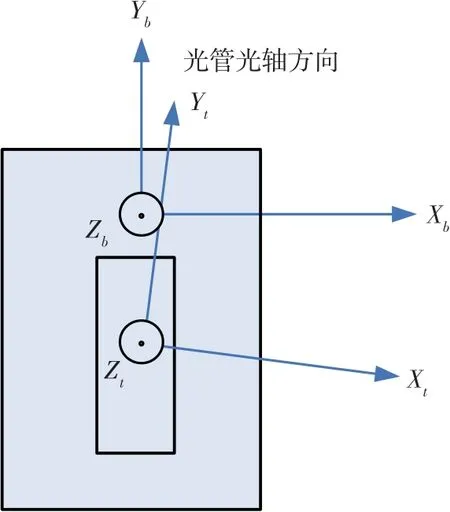
图3 光管坐标系与惯组坐标系安装关系示意图Fig.3 Schematic diagram of coordinate systerm relationship

自准直光管和激光捷联惯组在当地地理坐标系下的安装夹角可通过静态标定方式进行测量。

方位安装夹角:

俯仰安装夹角:

横滚安装夹角:

标定测量时先将激光捷联惯组的安装基面调整至水平状态,然后通过光学测量方法得到光管光轴在n系下的方位角ψt、俯仰角θt和横滚角γt,则ψ0、θ0和γ0可等效成光管坐标系相对惯组坐标系的角位置。类比公式（2）,可以得到t系和b系间的变换矩阵为

2.2.3 t 系和n 系间的变换

t系和n系间的角位置可以用ψ1、θ1和γ1表示,ψ1即为自准直光管光轴相对大地北向的夹角,θ1和γ1即为光管在n系下的俯仰角和横滚角。

通过b系为媒介,建立起t系和n系之间的关联,类比公式（2）,两个坐标系之间的转换矩阵为

3 瞄准角度解算

瞄准角度解算就是通过惯组瞄准设备的测量值获得目标棱镜方位角度的过程,解算过程如下:

3.1 获得光管光轴的方位角度和俯仰角度

激光捷联惯组对准完成后输出ψ、θ和γ,从而获得惯组输出姿态矩阵,根据自准直光管和激光捷联惯组的初始安装夹角获得初始安装矩阵,通过矩阵变换,可得到光管的输出姿态矩阵则光管光轴在n系下的ψ1、θ1和γ1可按公式（7）计算。

ψ1定义域为0°～ 360°,θ1和γ1定义域为-90°～90°。

3.2 获得光管准直偏差角度

自准直光管以光轴为基准,通过物镜发出平行的准直光束照射到目标棱镜上,其返回光束汇聚到处于物镜焦平面上的CCD 上,根据返回光点在CCD 上的偏移量即可求得光管光轴与目标棱镜的准直偏差角[5]

式中:β——准直偏差角;f——物镜焦距;L——返回光点在CCD 上的偏移量。

3.3 获得斜瞄方位修正角度

自准直光管与目标棱镜准直时,在斜瞄状态下会带来方位角偏差[6],需对其进行修正。

式中:δ——方位角偏差;λ——目标棱镜的棱线相对准直分划板横丝的不水平度[7],（″）。面对棱镜左高为正,其中,目标棱镜的棱线不水平度由箭上系统提供,准直分划板横丝的不水平度按公式（10）计算。

3.4 方位角度合成

对瞄准角度进行合成计算,目标棱镜的方位角Am按公式（13）计算。

当（ψ1+β-δ）大于360°时,K取-1;当（ψ1+β-δ）小于0°时,K取1,否则取0。

瞄准角度解算如图4 所示。

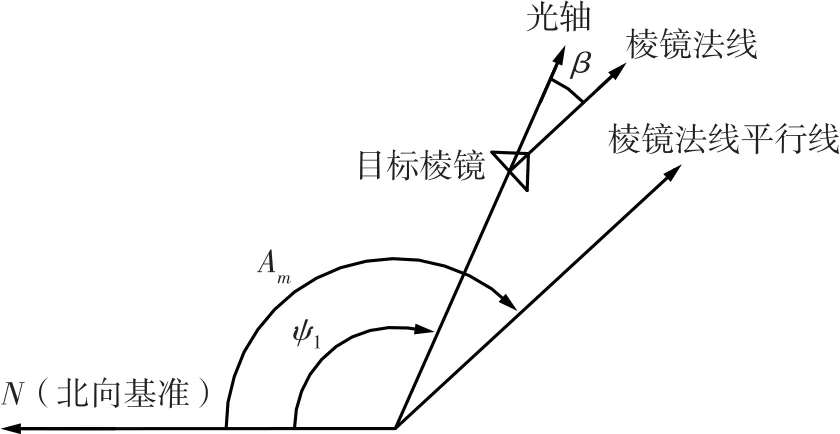
图4 瞄准角解算示意图Fig.4 Schematic diagram of aiming angle calculation

4 分析说明

（1）对θ1的取值极限情况和取值正负情况进行分析后,公式（8）可进一步优化为

（2）应使光管测量坐标系和t系保持严格一致,即光管内部CCD 安装方向与准直分划板横丝一致。使用时准直偏差角不宜过大,以减小耦合误差对方位测量值的影响。

（3）瞄准角度的解算方法同样适用于惯组导航状态下的动态测量,当惯组输出姿态角度发生变化时,解算出的光管输出姿态矩阵也相应变化,同时光管可动态敏感出相对目标棱镜的方位变化,要求数据更新频率不小于10 Hz。

5 验证

对工程样机进行了验证试验,将固连有CCD 自准直光管的激光捷联惯组（光管光轴初始安装夹角ψ0=34°,θ0=0.5°,γ0=0.1°）安装固定在三轴摇摆台上,惯组本体与三轴摇摆台基面一致,自准直光管前方近距离架设一宽尺寸目标棱镜,如图5 所示。

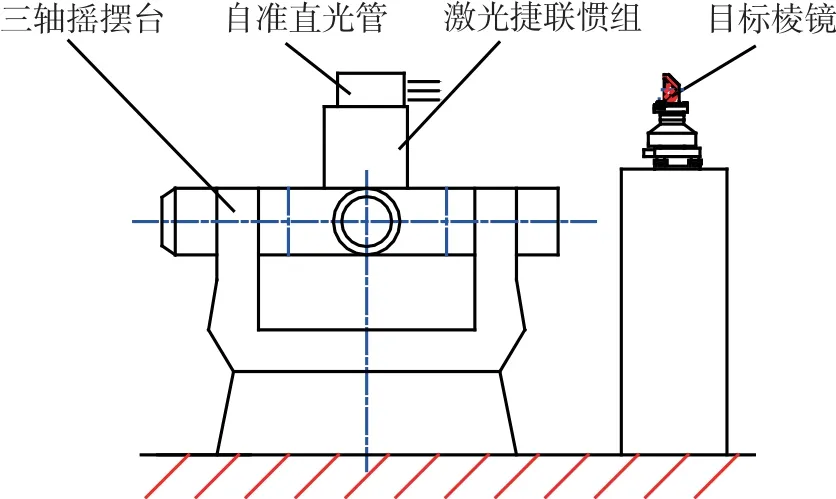
图5 验证试验示意图Fig.5 Schematic diagram of verification test

先将三轴摇摆台的姿态角度调整至零位,并使自准直光管与目标棱镜的准直偏差角度调整至零位附近。激光捷联惯组进行自主定向测量后,得到目标棱镜的方位测量值,然后在惯组导航状态下通过改变三轴摇摆台的姿态角度来模拟惯组本体的工况,并得到在不同工况下目标棱镜的方位测量值,如表1 所示。

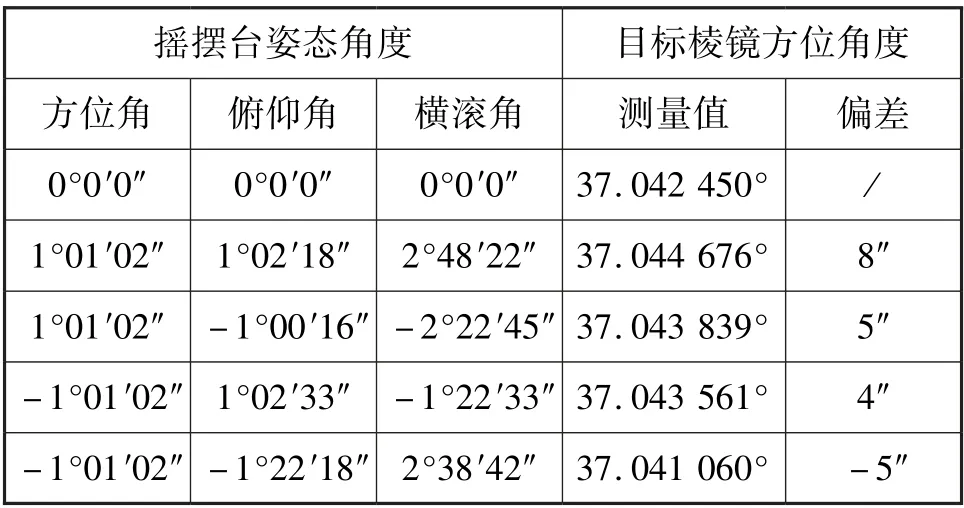
表1 瞄准解算验证试验数据Tab.1 Aiming calculation test data

试验表明,当惯组姿态角度发生变化时,对同一目标棱镜的方位测量值偏差不大于8″,此偏差值大都是由CCD 测量误差和标定误差等因素引起的,因此通过瞄准解算方法可有效消除方位耦合误差。

6 结束语

采用激光捷联惯组获得捷联惯组本体系相对导航坐标系（当地地理坐标系）间姿态矩阵,完成初始对准。自准直光管与激光捷联惯组固联,对惯组坐标系和光管坐标系进行标定,获得两者的初始安装矩阵。通过矩阵变换方式,将惯组输出姿态角转换成光管光轴在地理坐标系下的姿态角,消除了设备初始安装夹角带来的方位耦合误差,解决了无依托瞄准过程中的瞄准数据的解算问题。