考虑集卡到港时间延迟的堆场起重机动态调度研究
2023-05-26王耀宗,胡志华,田曦丹,陈婉婷
王 耀 宗, 胡 志 华, 田 曦 丹, 陈 婉 婷
(上海海事大学 物流研究中心, 上海 201306)
0 引 言
在自动化集装箱码头中,堆场面积占码头总面积的40%至60%,是码头重要的作业区域[1].自动化堆场连接岸边船舶的装卸与外集卡的运输,用于集装箱的堆存和中转,其作业效率制约码头的整体性能.为提升堆场的作业能力,码头采用穿越式双起重机的作业工艺,协同作业箱区内任意位置的装卸和堆垛任务[1].然而,在同一箱区作业的两台起重机可能发生干涉[2],即如果小起重机穿越正在某一贝位作业的大起重机或者两台起重机同时在同一贝位作业,将发生干涉.因此,起重机的调度计划应为一个无干涉的作业序列.
在集港作业中,集卡可能受交通拥堵等不确定因素的影响而延迟到港.通常,在集装箱船靠泊前的1~3 d,码头为准备装船的集装箱制订集港计划,集卡按照预约的时段依次到达堆场.然而,不确定因素可能导致集卡未能按照预约的时段到达堆场,实际交箱时间滞后于计划的交箱时间,对原有作业计划产生扰动.因此,码头需要及时调整作业计划以降低扰动前后规划结果的偏差.集卡延迟到港使得码头的调度作业具有动态性特征.码头通常以静态方式制订作业计划[3],即调度期初做好所有任务的起重机作业计划,但该作业模式的时效性较差,如果出现集卡到港时间延迟而产生即时请求,原有作业序列将不再满足最优性甚至不可行,影响堆场的作业效率.
在码头多级作业场景下,作业工序相互耦合与装卸决策相互依赖是设备调度的复杂性所在,而双起重机非交叉约束进一步增加了建模的难度[4].Vis等[5]把双起重机问题转化为单起重机问题进行求解;Gharehgozli等[6]把起重机的调度问题抽象为具有优先约束的多重旅行商问题;郑红星等[7]研究考虑倒箱的混堆装船箱区内起重机调度优化问题,提出了带滚动时域的启发式算法求解多起重机作业序列,并设计了带有解空间切割的遗传算法求解单个时域对应的子调度问题;Hu等[8]把起重机之间的安全距离转化为时间间隔以处理干涉,提出了混合整数规划模型和非线性模型刻画批次任务之间的顺序约束,并设计了精确算法和遗传算法求解起重机的作业计划;Han等[9]以提箱完成时间最短为目标建立起重机调度模型,优化装船过程中起重机的行驶路径;秦磊磊等[10]以最小化任务完成时间为目标建立考虑交接区缓冲贝位决策的双起重机调度混合整数规划模型,求解最优缓冲贝位的位置与起重机作业序列.以上研究为堆场起重机的调度优化提供了理论及方法上的参考.
一些研究考虑了不确定因素的码头作业场景.为降低集卡到港时间不确定对出口箱堆存和装船效率的影响,范厚明等[11]构建了双层混合整数规划模型优化出口箱位分配与起重机作业序列,通过不断平衡层与层之间的最优解优化堆场堆存和装船作业效率;针对码头装卸作业时间不确定性,孙玉姣等[12]以最小化作业完成时间、岸边无集卡与堆场无集卡的时间和为目标,建立了混合整数规划模型,研究了考虑装卸时间受作业顺序与位置等影响下码头生产调度问题,为码头提供动态场景下优化装卸作业的参考;范厚明等[13]关注交箱序列不确定的起重机调度问题,根据出口箱预约信息提出了新的堆存策略,建立了堆场箱位分配及多起重机调度集成优化模型,同时对于预约时段的长度及准确性对调度结果的影响做了鲁棒性分析,补充了不确定情景下码头的运作优化研究.此外,Dorndorf等[14]关注穿越式Triple-ASC调度,当一个任务完成或一个新任务到达时,动态调整调度计划以优化任务的分配和起重机的作业序列.
在动态调度问题的研究中,Pillac等[15]综述了动态车辆路径优化问题,着重研究了确定性、随机性两个特征组合下的车辆调度问题.针对客户路线变更的路径优化问题,Ozbaygin等[16]建立了混合整数规划模型,在迭代重优化框架内,基于初始计划动态调整路线变更后的计划;为了减小重调度对系统的扰动,宁涛等[17]从干扰管理角度研究了车辆行驶时间延迟问题,以最小化用户时间窗偏离度和最小化配送成本为目标建立了数学规划模型;针对自动导引车(AGV)动态调度问题,丁一等[18]采用周期和事件混合驱动的方式——根据AGV的状态定义若干触发规则响应突发事件,并结合周期型调度策略生成调度计划;杨珍花等[19]研究了甩挂车辆的动态调度问题,建立了挂车装卸时间不确定混合整数规划模型,并提出了多阶段动态优化算法生成牵引车的调度方案.
综上所述,关于动态车辆路径优化和柔性车间动态调度问题的研究已取得丰硕的成果.多数文献采用周期驱动或事件驱动的重调度方式处理延迟或紧急任务,即在特定时刻或状态下调整原有计划.然而,该重调度方式下,如何在复杂场景下界定事件的存在形式与如何选择调度时段长度是研究的难点,尤其在集装箱码头这一多级物流系统中,难以穷尽作业场景下所有状态及其对应事件.为此,本文在原有研究基础上,考虑在集卡到港时间延迟情形下的出口箱作业,以作业完成时间最短为目标,建立双起重机动态调度混合整数规划模型,提出一种迭代重优化框架处理延迟到港任务.由于存在非交叉约束,堆场起重机调度的难度显著增加,原有研究中,Ng[20]证明了其为NP-Hard问题.为了求解大规模作业计划,把遗传算法和贪婪插入算法纳入迭代重优化框架内,用遗传算法求解初始作业计划,用贪婪插入算法重优化延迟到港任务.贪婪插入算法的局部搜索技术具有快速生成最优解的优势,能够及时更新作业计划,响应动态性的要求.
1 动态调度问题描述
为了快速响应延迟到港任务需求,以降低对起重机调度结果的影响,把集港作业的调度期T划分为m个时段Ti,i∈{1,2,…,m},按照调度时段Ti的长度,把任务划分为多个批次的子任务φi,在调度期内分批次生成作业计划.一旦出现延迟到港任务的即时请求,根据其延迟到港时间,把该任务临机分配到相应的调度时段内,与该调度时段的原有计划一起执行重调度作业.基于此,提出迭代重优化框架,动态优化计划期内的任务,其关键是把延迟到港任务分配到某一调度时段内执行重调度,同时刷新该调度时段之后的若干批次作业计划.值得注意的是,把调度时段的划分和存在延迟任务的重调度纳入该框架内,降低了作业计划调整的难度与成本.基于迭代重优化框架的动态优化流程如下:

步骤2在零时刻下,向后生成3批作业计划Pi,即生成包括调度时段T1、T2、T3在内的3批作业计划P1、P2、P3.置i=1.


步骤5生成起重机作业计划Pi,记录完成集合Pi中所有任务的时刻t*.
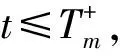
动态优化流程的核心是边作业边分配.即同一时刻起重机执行已分配的作业计划,同时码头为剩余的集港作业分配作业计划;此外,不断检测是否存在延迟任务,为延迟到港的集装箱临机分配作业计划,并重优化该调度时段内的作业计划.以上基于迭代更新的动态优化框架是调度优化模型及其优化算法设计的前提.在该动态优化框架下,每一时刻作业系统内仅存在少量的作业计划,不仅降低了计算成本,也保证了在小范围内为延迟到港集装箱任务分配作业计划的便利性,避免延迟到港的不确定性给系统带来较大的扰动.
2 调度优化模型
2.1 问题特征分析
本文研究的目标是优化集港作业内任务的分配与起重机的作业序列,最小化任务完成时间;如果存在延迟到港任务,则对原调度计划进行重优化,以保证调度计划的最优性,同时减少作业计划调整所产生的延误时间.因此,关键优化问题:(1)决策每个任务的执行者(起重机);(2)决策每台起重机执行任务的顺序;(3)如果调度计划存在干涉,执行规避干涉;(4)如果存在延迟到港任务,执行重优化.
2.2 变量定义
模型的基本符号及其变量定义如下:

Jd:延迟到港的任务集合,i,j∈Jd.
K:起重机k集合,k∈K,K={1,2}.
B:贝位b集合,b∈B,B={0,1,…,41}.
Oi,Di:任务i的起始贝位和目标贝位,Oi=0,Di∈B{0,41}.
Tij:起重机作业任意两个任务i、j之间的空载时间,i,j∈J.
Tv:起重机移动一个贝位的时间,Tv=u.
Tii:起重机作业任务i,从起始贝位Oi到目标贝位Di的移动时间,∀i∈J.
Ts:起重机提升或释放一个集装箱的服务时间,Ts=7.5u.
xkij:0-1变量.若起重机k依次作业任务i、j取1;否则取0.
yki:0-1变量.若任务i由起重机k作业取1;否则取0.
ski,eki:任务i由起重机k作业的开始、完成时间.
si,ei:任务i由起重机作业的开始、完成时间.
aij:0-1变量.若任务i的作业开始时间在任务j之前取1;否则取0.其中Oi=Oj,∀i,j∈J.
bij:0-1变量.若任务i的作业完成时间在任务j之前取1;否则取0.其中Di=Dj,∀i,j∈J.
2.3 模型建立

双起重机调度问题与车辆路径优化问题的建模机理一致,均有分配约束和序约束,即双起重机调度问题的分配约束确定起重机作业任务的集合,序约束确定每台起重机作业任务的顺序.不同的是,在堆场起重机调度问题上,需求是同质的,起重机也无容量约束.因此,将起重机作业任务的开始和完成时间作为求解该问题的主要决策,而该决策过程也是序约束的实现方式;另外,要求每个任务都被某一起重机作业,即对每一个任务而言,出度和入度相等且均为1.在不考虑起重机干涉的情况下,双起重机调度问题约束为
(1)
(2)
(3)
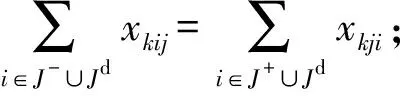
∀k∈K,∀j∈J∪Jd
(4)
eki≥ski+Tii+2Ts+(yki-1)M1;
∀i∈J∪Jd,∀k∈K
(5)
skj≥eki+Tij+(xkij-1)M1;
∀i∈J-∪Jd,j∈J+∪Jd,∀k∈K
(6)
ski≤ykiM1; ∀i∈J-∪Jd,∀k∈K
(7)
eki≤ykiM1; ∀i∈J-∪Jd,∀k∈K
(8)
(9)
式(1)确保有且仅有一个任务从虚拟起始任务处之后允许起重机作业,有且仅有一个任务在虚拟终止任务处结束作业;式(2)保证每一个任务只能由同一台起重机作业;式(3)确保起重机k作业任务i之后,紧接着作业任务j;式(4)保证每一个任务的出度和入度相等,即每一个任务被起重机作业;式(5)为任务作业的开始和完成时间的关系;式(6)约束起重机作业任务的先后关系;式(7)、(8)为作业时间上限约束;式(9)为M1的最小值.然而,由于干涉的存在,两台起重机的装卸决策相互依赖,约束(1)~(9)的优化结果可能出现无效解,即所得解包含干涉存在的形式.因此,为了生成无干涉的调度计划,基于以上所界定的干涉形式及其规避规则,约束两台起重机在同一贝位作业时的依赖关系,即:
(10)
(11)
aij+aji=1; ∀i,j∈J∪Jd,Oi=Oj,i≠j
(12)
bij+bji=1; ∀i,j∈J∪Jd,Di=Dj,i≠j
(13)
sj≥si+Ts+(aij-1)M1;
∀i,j∈J∪Jd,Oi=Oj,i≠j
(14)
ej≥ei+Ts+(bij-1)M1;
∀i,j∈J∪Jd,Di=Dj,i≠j
(15)
决策变量的取值如下:
ski,eki,si,ei≥0; ∀i∈J∪Jd,∀k∈K
xkij,yki,aij,bij∈{0,1}; ∀i,j∈J∪Jd
式(10)、(11)为任务作业的开始和完成时间;式(12)、(13)界定出现干涉情况,限定任务i或任务j其中一个完成时间较晚;干涉规避的同步约束如式(14)、(15)所示,限定位于同一贝位的两个任务作业开始和完成时间之间的依赖关系.
2.4 下界推导
双起重机调度问题求解的关键是计算单台起重机的作业序列,Vis等[21]提出了一种基于动态规划的最优下界推导方法,其目标是找到一条包含所有任务的起重机运行最短路径.基于Vis等[21]的下界推导方法,文献[5]证明了双起重机作业完成时间近似等于单台起重机作业所有任务时间(travel time)的一半.本文提出一种考虑两台起重机作业负载均衡的下界推导方法,使得所求的任务完成时间更接近所有任务作业时间的一半,缩小下界值与最优值之间的差距.增加整数决策变量pki,表示起重机k作业任务i的次序,即为序约束的关键决策,建立松弛模型计算下界flb.目标函数(16)是最小化两台起重机作业均衡条件下的完成时间,即下界flb.
(16)
(17)
(18)
pki-pkj+M2xkij≤M2-1;
∀i∈J-,∀j∈J,∀k∈K
(19)
1≤pki≤M2; ∀i∈J-,∀k∈K
(20)
M2=N
(21)
式(17)表示起重机在虚拟开始任务处作业,且任务必须分配给两台起重机;式(18)表示起重机作业任务量约束,为了均衡每台起重机的作业负载;式(19)、(20)表示每台起重机作业任务的序约束,用于消除子回路;式(21)表示M2的一个取值.
3 迭代重优化框架及其算法
3.1 迭代重优化框架
为了求解考虑集卡延迟到港的堆场起重机动态调度问题,在迭代更新的动态优化流程基础上,提出一种动态处理延迟到港任务的方法——迭代重优化框架及其算法.首先,在所划分的时段Ti内,依次生成对应批次任务的起重机作业计划;如果起重机在作业之前无延迟到港任务,则执行原有作业计划.一旦存在延迟到港任务,原有作业计划变得次优甚至不可行.因此,根据起重机作业进度和任务延迟到港时间,对特定批次任务进行重优化.重优化的前提是,定位延迟到港任务的到港时间落在哪个调度时段内,即延迟任务属于哪一批次的作业计划.然后,把延迟到港任务和该批次原有任务一起执行重优化生成更新的作业计划.简而言之,只要存在延迟到港任务,就会生成一批更新的作业计划.
基于此,设计两个优化算法支撑迭代重优化框架:遗传算法用于生成各时段所对应批次任务的作业计划;贪婪插入算法用于重优化带延迟到港批次任务的作业计划,生成更新的作业计划,应对动态性.贪婪插入算法具有快速搜索的特征,能够在遗传算法求解结果的基础上,把延迟到港任务插入原有作业计划序列中最合适的位置.迭代重优化框架及其算法构成如图1所示.以上算法的构成逻辑及其形成的闭环优化策略,其益处体现在3个方面:首先,遗传算法仅仅作用于特定批次的任务集合而不是全部任务集合,因此,搜索空间限定在较小的范围内,增加了搜索到全局最优解的可能性[22];其次,由于原有作业计划仅限定在某一批次任务,针对延迟到港任务,贪婪插入算法能够在其有限邻域内快速生成最优解,完成对应批次任务的重优化;最后,考虑延迟到港任务的重优化是基于某个批次的作业计划,重优化后生成的作业计划与原有作业计划形成较为平稳的过渡,避免由于作业计划大范围调整对起重机作业产生较大的扰动.
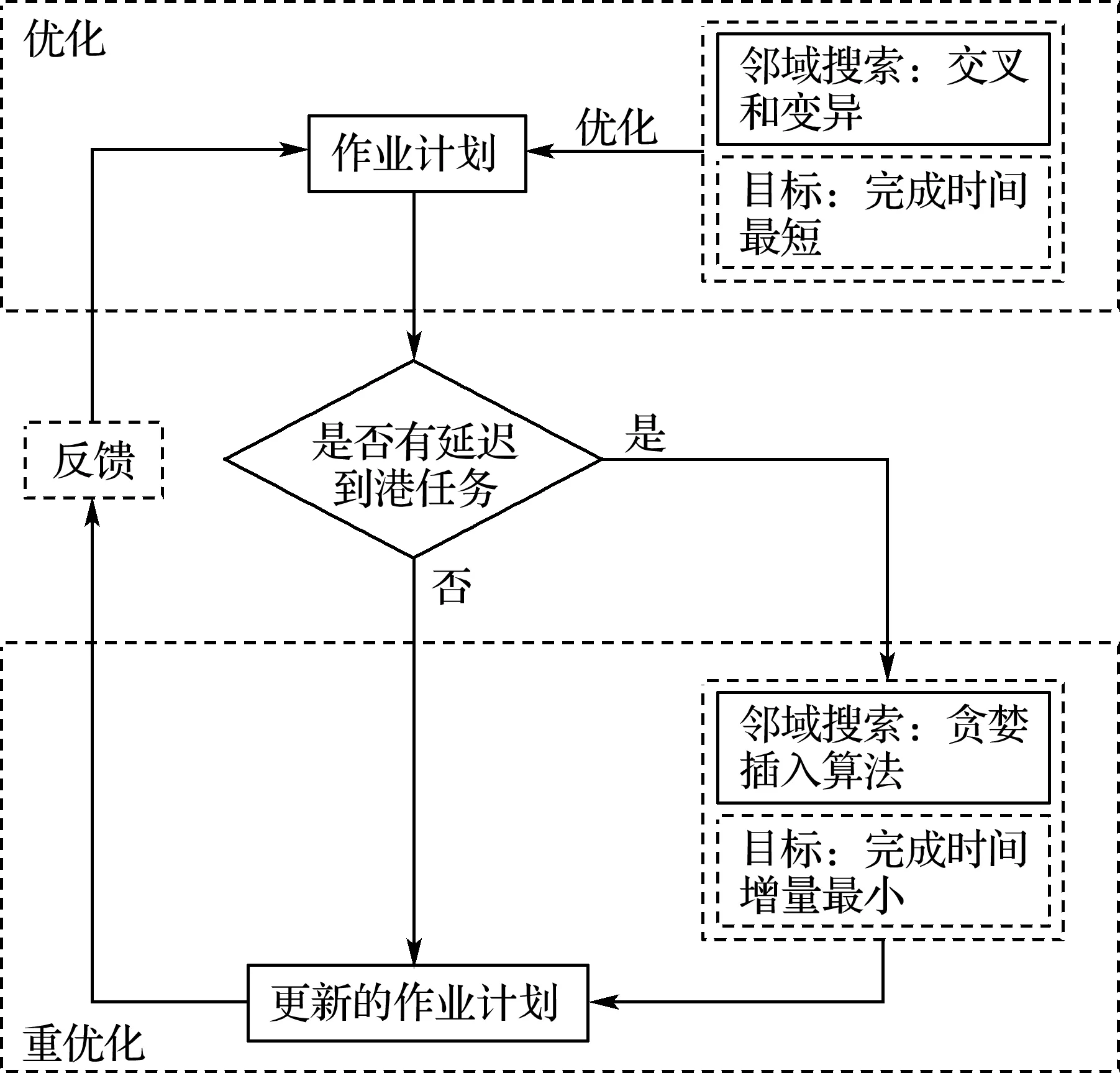
图1 迭代重优化框架及其算法
3.2 算法设计
(1)编码方式和解码策略
采用随机排列编码向量表示双起重机作业序列中的任务,即染色体上每一位元素(等位基因)都是互异的,代表一个作业任务,如图2所示.在解码过程中,根据染色体上等位基因的排列顺序依次确定起重机的作业序列.

图2 双起重机作业序列的染色体编码结构
遗传算法的解码策略是将编码向量转化为两台起重机的作业序列,以便利用适应度函数计算编码向量对应的评价值.根据双起重机作业的顺序约束和干涉规避约束,将编码向量转换为可行的双起重机作业序列,并使遗传算法的交叉算子和变异算子在全局范围内寻优,最终确定最优解.以某一批次的作业任务为例,说明解码策略及其对应的算法,如算法1所示.
算法1基于随机排列编码的解码策略
输入:(1)参数:[J,K,Oi,Di];
(2)随机排列序列:S0.
输出:(1)Sk:最优双起重机作业计划,∀k∈K;
(2)[ski,eki]:作业计划中,任务作业开始、完成时间,∀i∈J,∀k∈K;
(3)f:完成时间(makespan).
步骤1初始化:令f为足够大的实数;ski、eki置零.
步骤2forxinX.其中,X=|S0|.

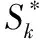
步骤2.3检测干涉的存在与执行规避.

步骤2.4分别计算两台起重机作业序列对应的完成时间f1*、f2*.
步骤2.5令f*=max(f1*,f2*).

步骤3输出f、Sk、ski、eki,i∈J,k∈K.
(2)贪婪插入算法
一旦存在延迟到港任务(即时请求),临机分配该任务到相近的调度时段内,用贪婪插入算法重优化该时段内原有作业计划.贪婪插入示意如图3所示,把新增任务依据完成时间增量最小的原则插入原有序列的相应位置.若存在多个新任务,则按照移动时间Tii从小到大进行递增排序,依次执行贪婪插入操作,如算法2所示.

图3 延迟到港任务重优化示意图
算法2迭代重优化框架下贪婪插入算法
输入:(1)参数:[J,K,Oi,Di];
(2)原有作业序列:Skp,∀k∈K,p∈Pi={pi,pi+1,pi+2};
(3)当前时刻:τ.
输出:(1)Pp:更新后的第p批次作业计划,∀p∈Pi;
(2)[ski,eki]:作业计划中,批次p作业的开始和完成时间,∀i∈J,∀k∈K.
变量:Bp,Ep:批次p作业计划的开始、完成时间;
δ:任务开始执行前,允许变更计划的最大持续时间.
步骤1零时刻下,产生3批作业序列,即初始作业计划Pp,完成时间为Ep,p∈{1,2,3}.令m=1.
步骤2起重机执行作业计划Pm.
步骤3在τ∈(Bm,Em)下,向后生成1批作业计划Pm+3.
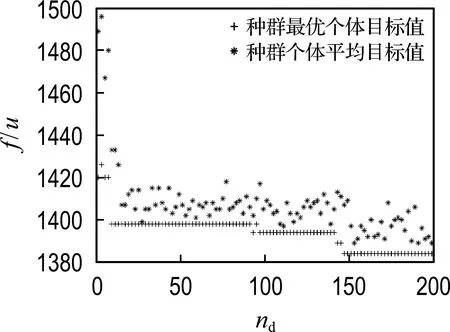
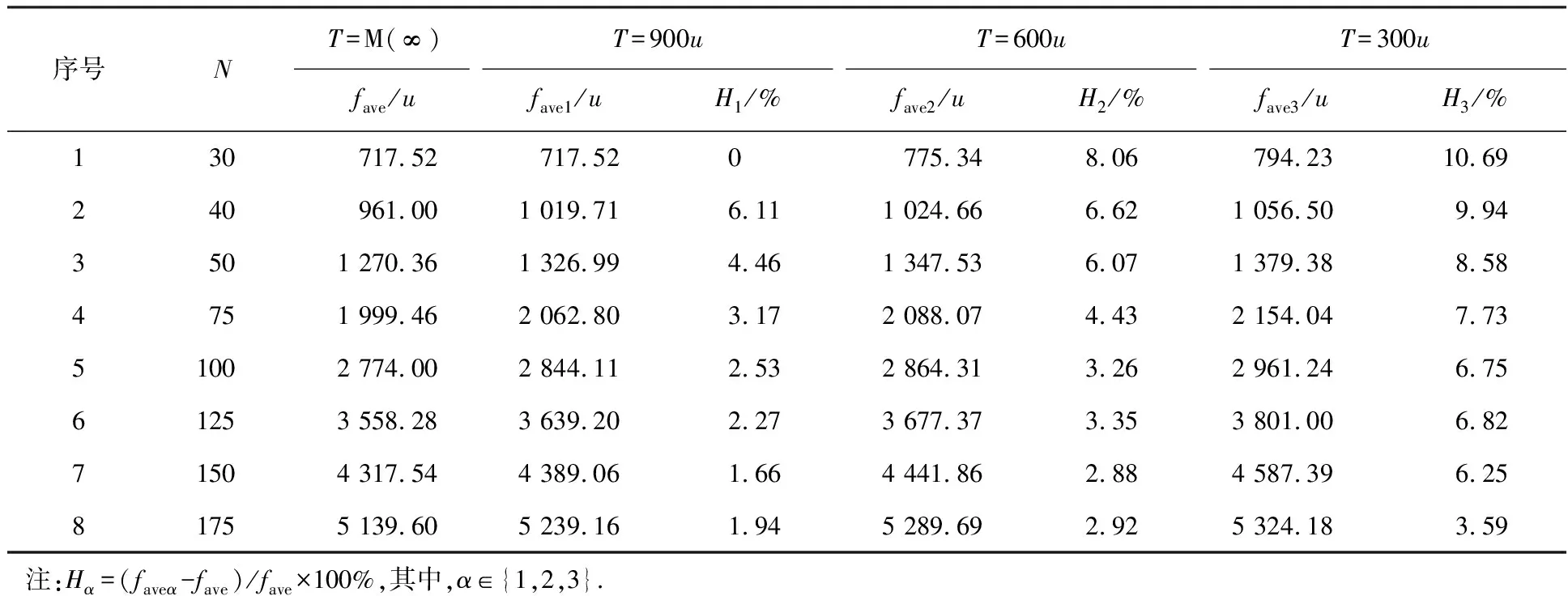
步骤4若延迟到港集装箱的到港时间落在第p批次作业计划中,即τ 步骤4.1把延迟到港任务集合N(j∈N)按照移动时间Tjj递增排序,依次执行插入操作.取l=arg mineki,把任务l插入序列Skp中,使完成时间的增量最小. 步骤4.2更新任务序列,Skp←Skp∪{l}. 步骤6生成重优化后的作业计划Pp,p={m+1,m+2}. 步骤7当τ≥Bm+1时,起重机执行作业计划Pm+1;令m←m+1,若m≤3,返回步骤3;否则,结束重优化. 设计多组算例验证堆场起重机调度模型和松弛模型的有效性、算法1的计算性能以及算法2的重优化性能.计算在Windows 10操作系统上用Python语言编程实现,计算机配置:Intel(R)Core(TM)i7-10510 CPU @1.8 GHz,16 GB RAM.用CPLEX作为模型求解的分支切割(branch-and-cut)求解器. 数据来源于自动化码头作业数据生成平台(https://www.instances.de/dfg/),分别生成多组小规模算例(N≤12)和大规模算例(N≤50).箱区规模为40贝位×6栈×5层.堆场起重机移动速度为3 m/s,即起重机在4 s(u)内通过一个贝位.另外,设起重机抓取或释放一个集装箱需要30 s(7.5u).对于起重机而言,其调度主要关注进口箱任务的起始贝位(Oi)和目标贝位(Di).由实例生成器导出的小规模算例(N=5)见表1. 表1 算例示例(N=5) 实验设计的目的及其相应设置见表2. 表2 实验设置 4.2.1 模型与算法有效性验证 模型和算法1的规划结果见表3.其中,flb表示松弛模型所计算的松弛解.结果显示,松弛解flb与最优解f1的最大误差为3.91%,说明松弛模型为该数学规划问题提供了一个良好下界,可作为模型和算法优化性能的评判基准.算法1与CPLEX所求得最优解之间的平均误差仅为0.49%;当任务规模增加到12时,CPLEX无法在可接受的时间内求得最优解,但算法1能够在较短时间内求得近似最优解.由此可见,算法1在求解双起重机调度问题上具备良好性能.此外,双起重机作业路径如图4所示,两台起重机在同一时间f同一贝位b下的(重载)路径无交点,表明模型的干涉规避约束有效. 4.2.2 算法参数调节与性能验证 为研究算法的参数取值对优化结果的影响,在[0,1]以步长0.1分别取交叉概率Pc和变异概率Pm,组合后获得非连续分布解的变化规律,如图5的等值线所示.由于算例结构的一致性,通过分析算法1在Pc和Pm组合下解的演变规律,限定参数的取值范围,以此作为其他实验中参数选择的依据,避免大范围参数调节造成的冗余计算影响求解效率. (a)最小值 为进一步验证算法1的计算性能,分别选取任务规模为30和50进行测试.不失一般性地,取不同的交叉和变异概率组合,减小固定交叉和变异概率对求解结果的局限性,计算结果见表4、5.计算结果表明,算法求解结果与松弛模型下界之间的平均误差均不超过2%;另外,图6为算法求解任务规模为50的收敛曲线,在150代内收敛到最优目标值.因此,在优化结果和计算时间两方面验证了算法具备的良好优化性能. 表4 大规模算例下算法1的规划结果(N=30) 表5 大规模算例下算法1的规划结果(N=50) 图6 算法1的收敛图 4.2.3 迭代重优化框架有效性验证与分析 在迭代重优化框架下,把某一时间段内的集港作业划分为若干调度时段,使出口箱任务分别在相应的调度时段内生成作业计划,一旦出现延迟到港集装箱的即时请求,可临机分配至与到港时间最近的调度时段内.为验证该框架的有效性,依次取不同长度的调度时段和不同延迟到港的箱量,求解相应的规划结果. (1)调度时段长度对规划结果的影响 调度时段长度T分别取M、900u、600u和300u,其中M表示不对集港作业进行拆分.规划结果如表6、图7所示,可见:调度时段长度越小,作业完成时间越长,但计算时间明显缩短.因此,均衡解的质量与计算时间,选取合适的调度时段长度有利于提高码头制订作业计划的效率. 表6 调度时段长度对规划结果的影响 (a)作业完成时间 (2)延迟到港的箱量分析 定义延迟程度β表示某一交箱时段内延迟到港箱量Nd与原始箱量No的比值,即β=Nd/No.以调度时段T为基准,用算法1生成基础作业计划,调用算法2对延迟到港任务执行重调度,计算结果如图8所示. 图8 延迟到港箱量对规划结果的影响 结果显示,延迟到港箱量占比β越大,作业时间的增量Δ越大;而随着调度时段T的减小,这一影响逐渐弱化.其原因在于,随着延迟任务的数量增加,重调度对原作业计划的扰动增大,可行解数量减少(或增加)的变化幅度增大;而缩短调度时段,有利于为延迟到港任务分配更适合的调度时段,从而增加重调度结果需求到最优解的可能性. 自动化集装箱码头的堆场作业受诸多外部不确定因素的干扰,制约作业效率的提升,如交通拥堵、雨雪天气影响集卡的到达时间,对原有作业计划产生扰动.针对集卡到港时间延迟的堆场起重机动态调度问题,本文提出了迭代重优化框架,把集港作业的调度期划分为多个时段,出口箱任务分别在相应的时段内被安排作业,一旦出现延迟到港集装箱的即时请求,可临机分配至与到港时间邻近的时段内执行重调度.借助自动化码头作业数据生成平台,构造小规模和大规模算例,验证本文提出的模型和算法的有效性.通过结果分析验证了模型和算法的有效性,并提出两方面有益于码头运作优化的管理启示. 一方面,在计划制订之前,若待作业的任务量较少,调度人员可增大调度时段长度,以保证解的质量,缩短作业的持续时长;若任务量较多,可适当减小调度时段长度,从而缩短计算时间以提高计算效率.另一方面,码头运营者需及时与客户沟通,获取集卡的行驶状况、预计到达堆场的时间等信息,为可能延迟到港的集卡提前部署应对策略:当延迟到港箱量占比较小时,可适当增大调度时段长度,保证整体作业水平;当延迟到港箱量占比较大时,可减小调度时段长度从而降低重调度对作业系统的扰动. 本文研究还存在一些不足,即便是分段调度提供了应对集卡作业不确定性的方式,但难以快速消除集卡到港动态性对系统的扰动.未来的研究可结合强化学习方法,在历史作业数据中学习相关场景下的调度经验,从而及时、准确地调用相应策略生成或调整作业计划.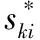
4 数值实验
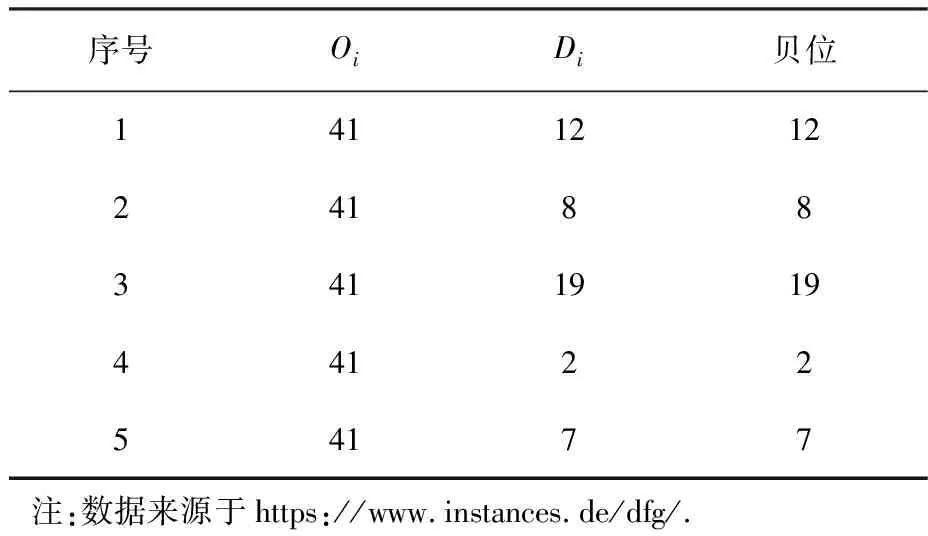
4.1 实验设计
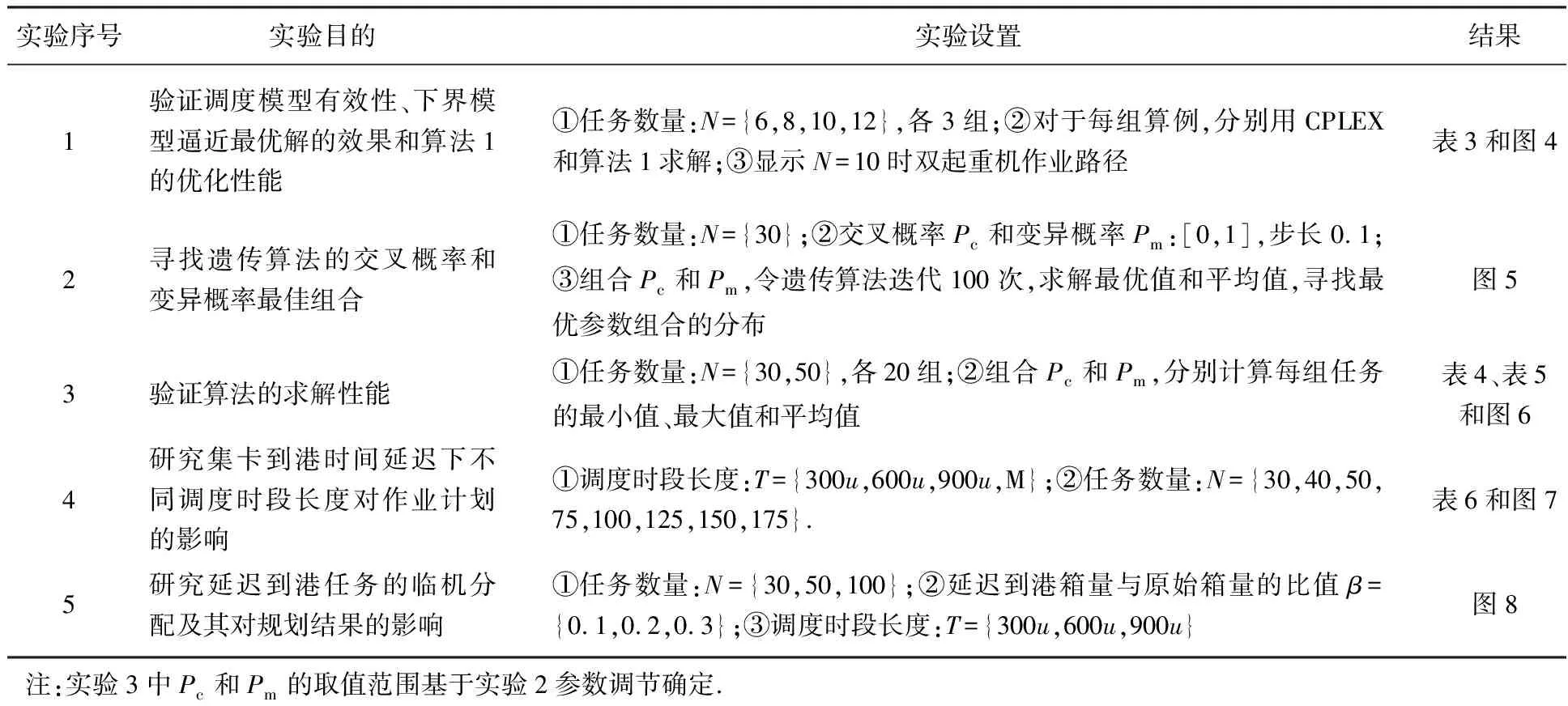
4.2 实验结果与分析






5 结 语
