陶瓷膜微滤有机溶液的滤饼阻力影响因素研究

宋继田, 史慧言, 杨 扬, 蔡开街, 高泽康, 刘 旭

(1. 天津科技大学 机械工程学院, 天津 300222; 2. 天津市轻工与食品工程机械装备集成设计与在线监控重点实验室, 天津 300222; 3. 天津樱桃谷农业科技发展有限公司, 天津 300000; 4. 珠海市格力电器股份有限公司, 珠海 519070)

膜分离技术在众多领域都表现着优异的性能,为高效分离或浓缩有机溶液提供了完美的解决方案,相比于传统工艺,它有着高效、清洁与操作方便等优点,在食品加工、污水处理和医药生产等方面被广泛使用[1-2].陶瓷膜作为无机膜中最为常用的一种,更有着化学性质稳定、机械强度大、使用寿命长等优势,可以在具有强氧化性和强酸等极端条件下正常运行[3].尽管膜分离技术在各方面表现都十分良好,却在使用方面存在一个近乎致命的问题——膜污染.膜污染会出现减小膜的有效过滤孔径、增大截留率等情况,简要来说就是减少膜的有效使用时长[4-6].另外,膜污染问题也会降低陶瓷膜过滤性能,并导致膜组件属性的永久性变化[7],增加设备的运行费用和维护费用,这些因素都影响了膜分离技术的推广应用.

如今,膜污染机理的研究已经成为本领域的研究热点.膜污染问题成为膜分离技术实际应用过程中的重要阻碍,十分影响膜组件的寿命,膜组件的不断更换又是制约膜技术推广的主要问题之一[8].因此,探索能保持膜设备效率和使用寿命的最佳操作条件,通过分析各参数对滤饼阻力的影响,避免实际应用中对膜设备性能不利的操作,是膜分离技术在有机溶液中广泛应用的关键,也能够为膜技术的进一步推广清除障碍.

微滤是一种以低压差为动力、利用多孔性材料薄膜进行分离的膜过程,允许大分子有机物和无机盐等通过[9-11].本文选用蛋白和酵母颗粒两种典型物料配制溶液作微滤过滤规律的基本成分,以简化进料状况,使用错流过滤装置进行一系列实验,采用单因素实验与响应面优化法[12]考查各因素对于滤饼阻力的影响,着重从膜污染规律方面做研究,从而为工业上微滤系统的使用提供可靠的理论依据.

1 实验部分

1.1 实验材料

蛋白和酵母由南京草本源生物科技有限公司提供,产品硝酸与烧碱作为清洗剂来使用,氯化钠用来配制稀溶液以增加蛋白的溶解度,材料皆为分析纯规格.

陶瓷膜由法国TAMI公司生产(材质:TiO2;长度:1 178 mm;内径:2.96 mm;外径:25 mm;通道数:19;单只陶瓷管过滤面积:0.212 m2;过滤精度:1.0 μm),膜壳及原料罐由天津科建科技发展有限公司生产(装填膜支数:3支;不锈钢316L,容积:0.1 m3),循环泵由南京日新流体技术有限公司生产,规格为SCP-10A-175-3AA.

1.2 实验装置及方法

建立如图1所示装置,采用内压错流过滤方式,以考查陶瓷膜过滤性能.

1.储料罐;2.进料泵;3.循环泵;4.陶瓷膜组件;5.换热器;6.压力表;7.流量计;8.温度传感器图1 错流过滤流程图Fig.1 Flow chart of cross-flow filtration

将料液浓度为2 g/L蛋白和2 g/L酵母等比例配制的原料液由进料泵提供动力通入循环管道内,经循环泵提供循环动力将浓缩后的原料液带回原料罐中,澄清液经陶瓷膜组件过滤后在侧边出口收集,控温装置由换热器通过冷却水来实现.

1.3 响应面实验设计

根据Box-Benhnken中心组合设计原理[13-15],以单因素实验结果为依据,选择透膜压差(A)、切向流速(B)、料液浓度(C)、料液温度(D)为因子,以滤饼阻力(Y)作为响应指标,设置过滤时间为5 min,进行响应面回归模型设计.因素水平设计见表1 .

表1 实验设计因素与水平值Table 1 Experimental design factors and level values

1.4 实验数据的处理

(1) 膜通量计算

(1)

式中:J是料液的渗透通量,m/s;A是膜的实际过滤面积,m2;dV是清液体积,m3;dt是过滤单位时间,s.

(2) 滤饼阻力计算

(2)

式中:R是膜阻力,1/m;Δp是透膜压差,Pa;μ是渗透液黏度,Pa·s;J是料液的渗透通量,m/s.

首先用纯水做透水实验,得出膜本身阻力,然后以蛋白和酵母配制的原料液测出膜的总阻力,通过阻力串联定律,从而得出滤饼阻力[16].

2 结果与讨论

2.1 纯水通量实验

控制切向流速为3 m/s,温度为35 ℃,考察透膜压差对1 μm孔径的膜纯水通量的影响,结果如图2所示.

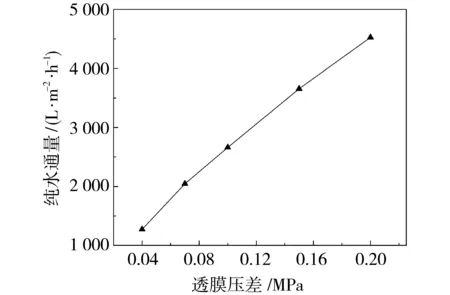
图2 透膜压差对纯水通量的影响Fig.2 Effect of membrane pressure difference on pure water flux

随着透膜压差的增加,膜通量基本呈现线性增长趋势.当跨膜压差由0.04 MPa增加到0.2 MPa,膜通量由1 270 L/(m2·h)增大到4 626 L/(m2·h),这主要是因为微滤过程的推动力为压差,当陶瓷膜处理纯水时,不会受到吸附、浓差极化、堵塞等膜污染因素的影响,纯水通量只受操作条件的影响,在料液浓度不变的情况下,纯水通量主要由跨膜压差决定.

2.2 操作参数对滤饼阻力的影响

2.2.1过滤时间对滤饼阻力的影响

浓度为2 g/L蛋白、2 g/L酵母的料液在透膜压差0.1 MPa、切向流速3 m/s、料液温度35 ℃的状态下,滤饼阻力随时间变化的关系如图3所示.

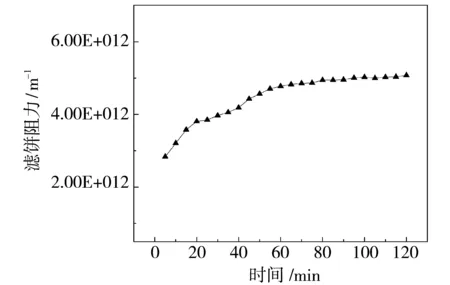
图3 滤饼阻力随时间的变化关系Fig.3 Variation of filter cake resistance with time

由图3可知,滤饼阻力值呈先增长后平缓的趋势,造成这种情况的原因是:在污染物接触膜的那一刻,各部分膜污染已经开始,起初膜表面还没有滤饼形成,料液中直径较小的颗粒会进入孔中分别堵塞或吸附在孔深处,之后很快有一部分颗粒吸附在膜表面形成最初的滤饼层,这是造成滤饼阻力快速上升的原因.中期阶段,滤饼层不断堆积增加厚度,以致细小颗粒进入孔深处的数量越来越少,此时滤饼阻力依然在增长.过滤后期,当滤饼厚度增长到一定值,滤饼层堆积速度与切向流速的带走速度达到一个平衡,厚度就不再有明显变化,但随着过滤的进行,滤饼中会进入更小的颗粒,滤饼孔隙率不断减小,滤饼不断被压实,此阶段滤饼阻力缓慢增长至平衡.

2.2.2透膜压差对滤饼阻力的影响

浓度为2 g/L蛋白、2 g/L酵母的料液在切向流速3 m/s、料液温度35 ℃时,不同压差下,滤饼阻力随时间的变化关系如图4所示.

图4 不同压差下滤饼阻力随时间的变化关系Fig.4 Variation of filter cake resistance with time at different differential pressures

由图4可知,压差为0.07、0.1、0.15 MPa情况时的3条线比较集中,说明这期间压差的变化对滤饼阻力影响不是很大.压差为0.04 MPa时阻力值普遍小是由于渗透压差过小,膜阻力本身占比很大,导致膜通量很低,会使滤液中的颗粒接触很慢,导致滤饼的增长程度十分有限.而压差为0.2 MPa情况下因阻力值影响使膜通量过大,颗粒与膜表面接触速度过快,滤饼形成速度会快很多且会生成较厚的滤饼层,较高压差便会造成浓差极化阻力增加,所以滤饼阻力有所上升.

2.2.3切向流速对滤饼阻力的影响

浓度为2 g/L蛋白、2 g/L酵母的料液在透膜压差0.1 MPa、料液温度35 ℃时,不同切向流速下,滤饼阻力随时间的变化关系如图5所示.

图5 不同切向流速下滤饼阻力随时间的变化关系Fig.5 Variation of filter cake resistance with time at different tangential flow rates

由图5可知,滤饼阻力随着切向流速的增加逐渐减少.切向流速直接影响滤饼的生成速度,相同情况下,切向流速越高,滤饼层厚度越薄,导致滤饼的整体阻力下降.但过高的切向流速下,滤饼阻力沿膜长度的分布不均,造成膜通量下降,从而表现为滤饼阻力下降不明显,陶瓷管越长,此现象越明显.

2.2.4料液浓度对滤饼阻力的影响

在透膜压差0.1 MPa、切向流速3 m/s、料液温度35 ℃时,不同料液浓度下,滤饼阻力随时间的变化关系如图6所示.

图6 不同料液浓度下滤饼阻力随时间的变化关系Fig.6 Variation of filter cake resistance with time for different feed liquid concentrations

由图6可知,滤饼阻力的快速增长期在20 min之内,也就是说在20 min内形成滤饼原型,之后不断有较小的颗粒进入到滤饼层中,压实滤饼增加滤饼层阻力.中间3个条件下的滤饼阻力曲线较为集中.料液浓度的上升首先会带来浓差极化阻力上升,相同时间内接触到膜表面的颗粒量就增加,导致滤饼层厚度随料液浓度有一个明显的上升,从而滤饼层对小直径颗粒起到的预过滤就越强,即进入膜孔内部的颗粒数量会减少,结果就是滤饼阻力随料液浓度的上升会有明显的增大.而后随着滤饼厚度增长越多,进入膜孔内的颗粒量越少,因浓度的增加会使得料液内的小直径颗粒数量增加,某个时刻滤饼厚度将达到增长上限.因此,滤饼阻力随料液浓度的增大呈现起初快速增加随后缓慢增长的趋势.

2.2.5料液温度对滤饼阻力的影响

浓度为2 g/L蛋白、2 g/L酵母的料液在透膜压差0.1 MPa、切向流速3 m/s时,不同料液温度下,滤饼阻力随时间的变化关系如图7所示.

图7 不同料液温度下滤饼阻力随时间的变化关系Fig.7 Variation of filter cake resistance with time at different feed liquid temperatures

由图7可知,在整个过程中滤饼阻力值随料液温度的升高有所下降.这是因为本系统控制温度是靠着膜过滤产生的热量升温,通过调节冷却水的流量降温,由于初始温度相同,以至于初始过滤时滤饼阻力相差很小,5种温度下的阻力变化曲线十分有限,这说明小范围的温度变化并不能给流动阻力带来特别的影响.在有机溶液过滤中,应考虑有机物的活性温度范围,不应为减小过滤阻力而破坏活性.

2.3 响应面法优化结果分析

响应面回归模型实验结果和方差分析结果见表2和表3.采用Design-Expert 12软件中的Box-Benhnken程序进行分析,获得二次多元回归方程:

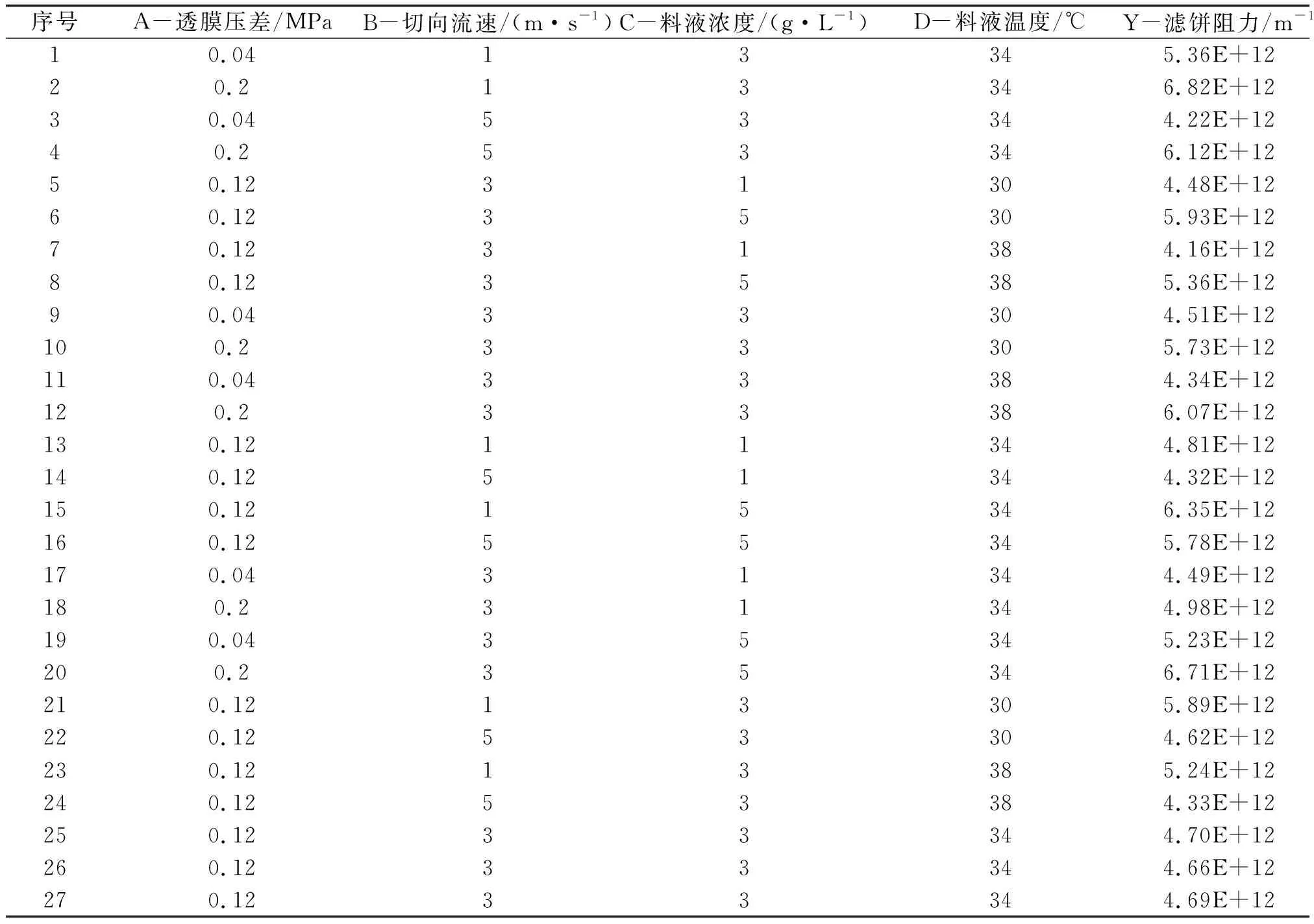
表2 滤饼阻力响应面分析方案及实验结果Table 2 Response surface analysis scheme and experimental results of filter cake resistance

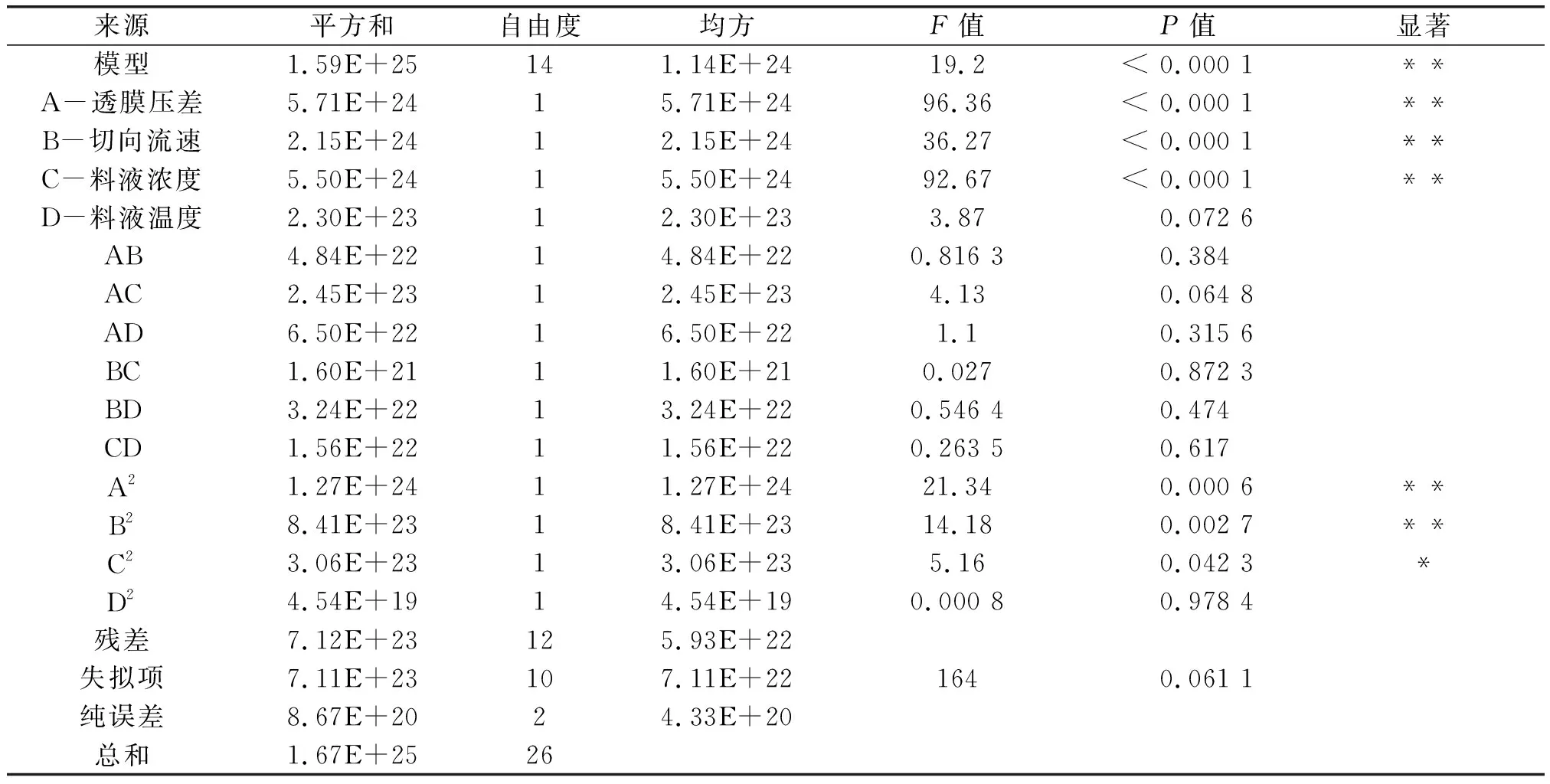
表3 回归方程的方差分析结果Table 3 Variance analysis results of regression equation

Y=4.683×1012+6.9×1011A-4.233×1011B+6.767×1011C-1.383×1011D+1.1×1011AB+2.475×1011AC+1.275×1011AD-2×1010BC+9×1010BD-6.25×1010CD+4.871×1011A2+3.971×1011B2+2.396×1011C2-2.917×109D2.

由表3可知,该模型P值<0.000 1,说明该回归方程具有良好的拟合度,认为该模型是稳定的.其中A、B、C、A2、B2对应的响应值影响极显著(P<0.01),C2对应的响应值影响显著(P<0.05),而D、AB、AC、AD、BC、BD、CD、D2为不显著因素(P>0.05).各影响因素对滤饼阻力的影响性排序为透膜压差(A)>料液浓度(C)>切向流速(B)>料液温度(D).

图8(a)表示滤饼阻力的残差图,可以看出残差图趋势大概是服从正态分布的,近似值均为0,可以确认该模型的适合性.使用残差预测图检验[见图8(b)],可以看出实验点沿着水平轴线上下随机变化,该模型没有显示出失拟和弯曲现象,并且测量值与预测值之间的差值很小,说明回归模型能准确说明实际观测结果.

图8 滤饼阻力残差的正态图和检验图Fig.8 Normal and check plots of filter cake resistance residuals

图9分别显示了6组以滤饼阻力为响应值的响应面和等高线趋势图.等高线图可直观反映出各因

素交互作用对滤饼阻力的影响,其中交互作用AC> AD>AB>BD>CD>BC.

2.4 最佳工艺条件

在目前的装置条件下,通过Design-expert实验设计软件模型的响应面优化所获得的最佳操作工艺参数为:透膜压差0.067 2 MPa、切向流速3.974 m/s、料液浓度1.159 g/L、料液温度38 ℃时,预测滤饼阻力(3.908E+12) (1/m).见图10.

图10 模型的响应优化图Fig.10 Response optimization diagram of the model

3 结论

1) 本实验通过单因素实验设计研究各操作参数与滤饼阻力的关系变化,结果表明:滤饼阻力与过滤时间、透膜压差、料液浓度成正比,与切向流速、料液温度成反比.

2) 本实验以滤饼阻力为响应指标,以蛋白和酵母颗粒两种典型物料配制有机溶液,在透膜压差为0.04～0.2 MPa、切向流速为1～5 m/s、料液浓度为1～5 g/L、料液温度为30～38 ℃时,经过响应面优化,得出目前装置条件下综合各参数使得滤饼阻力最佳的工艺条件为:透膜压差为0.067 2 MPa、切向流速为3.974 m/s、料液浓度为1.159 g/L、料液温度为38 ℃,预测滤饼阻力为(3.908E+12) (1/m).影响滤饼阻力的因素排序为:透膜压差(A)>料液浓度(C)>切向流速(B)>料液温度(D).

3) 虽然在透膜压差或切向流速方面稍作变化可以减小滤饼阻力,得到更高的膜通量,但过度的变化可能会进一步加强滤饼厚度以及浓差极化现象,而且增加的膜效率并不明显,不仅带来能源的浪费,也会减小膜的使用寿命,所以应综合考虑所研究物料的特性以选择最合适的操作参数.