方中有数，平淡为真

雷小华

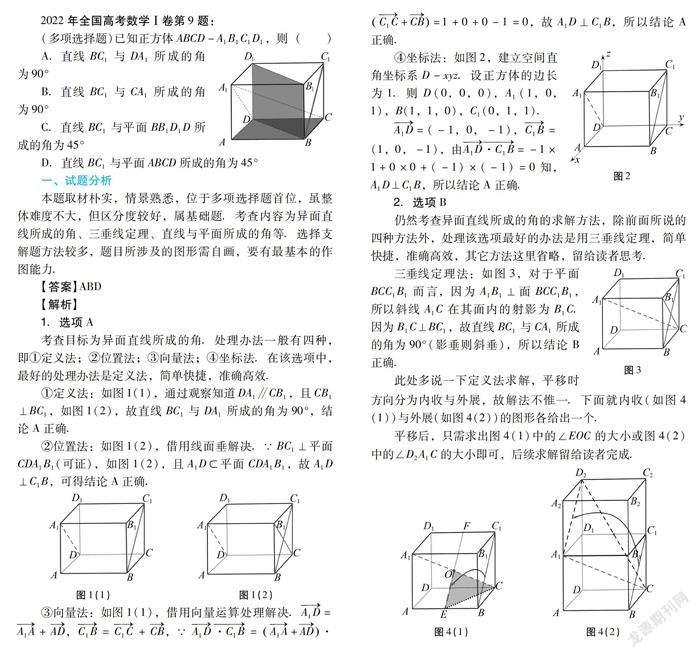
2022年全国高考数学Ⅰ卷第9题：

（多项选择题）已知正方体ABCD-A1B1C1D1，则（）

A.直线BC1与DA1所成的角为90°

B.直线BC1与CA1所成的角为90°

C.直线BC1与平面BB1D1D所成的角为45°

D.直线BC1与平面ABCD所成的角为45°

一、试题分析

本题取材朴实，情景熟悉，位于多项选择题首位，虽整体难度不大，但区分度较好，属基础题.考查内容为异面直线所成的角、三垂线定理、直线与平面所成的角等.选择支解题方法较多，题目所涉及的图形需自画，要有最基本的作图能力．

【答案】ABD

【解析】

1.选项A

考查目标为异面直线所成的角.处理办法一般有四种，即①定义法；②位置法；③向量法；④坐标法.在该选项中，最好的处理办法是定义法，简单快捷，准确高效．

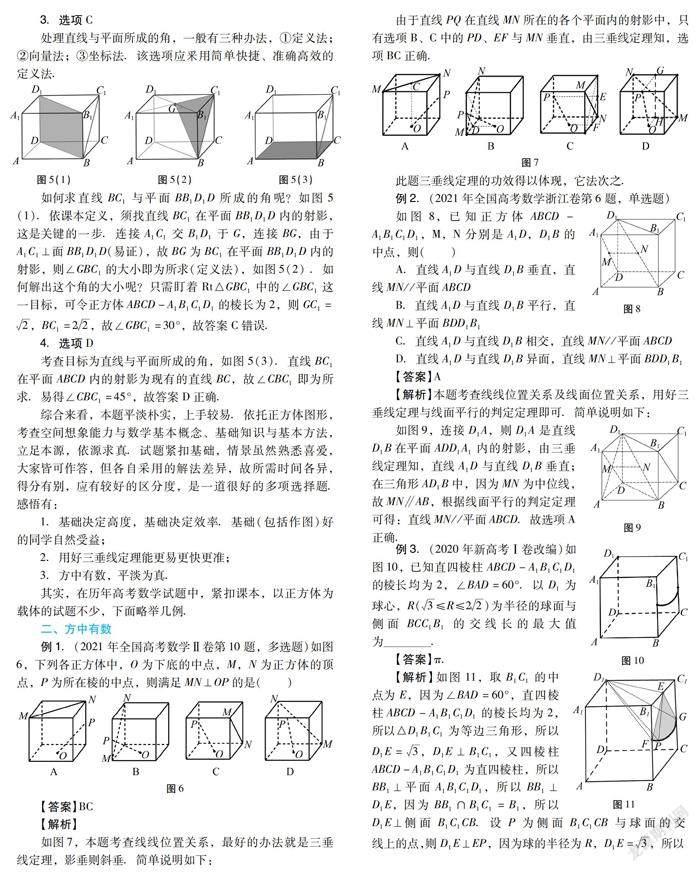
①定义法：如图1（1），通过观察知道DA1∥CB1，且CB1⊥BC1，如图1（2），故直线BC1与DA1所成的角为90°，结论A正确．

②位置法：如图1（2），借用线面垂解决.∵BC1⊥平面CDA1B1（可证），如图1（2），且A1D平面CDA1B1，故A1D⊥C1B，可得结论A正确．

③向量法：如图1（1），借用向量运算处理解决.A1D=A1A+AD，C1B=C1C+CB，∵A1D·C1B=A1A+AD·C1C+CB=1+0+0-1=0，故A1D⊥C1B，所以结论A正确．

④坐标法：如图2，建立空间直角坐标系D-xyz.设正方体的边长为1.则D（0，0，0），A1（1，0，1），B（1，1，0），C1（0，1，1）．

A1D=（-1，0，-1），C1B=（1，0，-1），由A1D·C1B=-1×1+0×0+（-1）×（-1）=0知，A1D⊥C1B，所以结论A正确．

2. 选项B

仍然考查异面直线所成的角的求解方法，除前面所说的四种方法外，处理该选项最好的办法是用三垂线定理，简单快捷，准确高效，其它方法这里省略，留给读者思考．

三垂线定理法：如图3，对于平面BCC1B1而言，因为A1B1⊥面BCC1B1，所以斜线A1C在其面内的射影为B1C.因为B1C⊥BC1，故直线BC1与CA1所成的角为90°（影垂则斜垂），所以结论B正确．

此处多说一下定义法求解，平移时方向分为内收与外展，故解法不惟一.下面就内收（如图4（1））与外展（如图4（2））的图形各给出一个．

平移后，只需求出图4（1）中的∠EOC的大小或图4（2）中的∠D2A1C的大小即可，后续求解留给读者完成．

3.选项C处理直线与平面所成的角，一般有三种办法，①定义法；②向量法；③坐标法.该选项应釆用简单快捷、准确高效的定义法．

如何求直线BC1与平面BB1D1D所成的角呢？如图5（1）.依课本定义，须找直线BC1在平面BB1D1D内的射影，这是关键的一步.连接A1C1交B1D1于G，连接BG，由于A1C1⊥面BB1D1D（易证），故BG为BC1在平面BB1D1D内的射影，则∠GBC1的大小即为所求（定义法），如图5（2） .如何解出这个角的大小呢？只需盯着Rt△GBC1中的∠GBC1这一目标，可令正方体ABCD-A1B1C1D1的棱长为2，则GC1=2，BC1=22，故∠GBC1=30°，故答案C错误．

4.选项D

考查目标为直线与平面所成的角，如图5（3）.直线BC1在平面ABCD内的射影为现有的直线BC，故∠CBC1即为所求.易得∠CBC1=45°，故答案D正确．

综合来看，本题平淡朴实，上手较易.依托正方体图形，考查空间想象能力与数学基本概念、基础知识与基本方法，立足本源，依源求真.试题紧扣基础，情景虽然熟悉喜爱，大家皆可作答，但各自采用的解法差异，故所需时间各异，得分有别，应有较好的区分度，是一道很好的多项选择题.感悟有：

1.基础决定高度，基础决定效率.基础（包括作图）好的同学自然受益；

2.用好三垂线定理能更易更快更准；

3.方中有数，平淡为真．

其实，在历年高考数学试题中，紧扣课本，以正方体为载体的试题不少，下面略举几例．

二、方中有数

例1.（2021年全国高考数学Ⅱ卷第10题，多选题）如图6，下列各正方体中，O为下底的中点，M，N为正方体的顶点，P为所在棱的中点，则满足MN⊥OP的是（）

【答案】BC

【解析】

如图7，本题考查线线位置关系，最好的办法就是三垂线定理，影垂则斜垂.简单说明如下：

由于直线PQ在直线MN所在的各个平面内的射影中，只有选项B、C中的PD、EF与MN垂直，由三垂线定理知，选项BC正确．

此题三垂线定理的功效得以体现，它法次之．

例2.（2021年全国高考数学浙江卷第6题，单选题）

如图8，已知正方體ABCD-A1B1C1D1，M，N分别是A1D，D1B的中点，则（）

A.直线A1D与直线D1B垂直，直线MN//平面ABCD

B.直线A1D与直线D1B平行，直线MN⊥平面BDD1B1

C.直线A1D与直线D1B相交，直线MN//平面ABCD

D.直线A1D与直线D1B异面，直线MN⊥平面BDD1B1

【答案】A

【解析】本题考查线线位置关系及线面位置关系，用好三垂线定理与线面平行的判定定理即可.简单说明如下：

如图9，连接D1A，则D1A是直线D1B在平面ADD1A1内的射影，由三垂线定理知，直线A1D与直线D1B垂直；在三角形AD1B中，因为MN为中位线，故MN∥AB，根据线面平行的判定定理可得：直线MN//平面ABCD.故选项A正确．

例3.（2020年新高考Ⅰ卷改编）如图10，已知直四棱柱ABCD-A1B1C1D1的棱长均为2，∠BAD=60°.以D1为球心，R（3≤R≤22）为半径的球面与侧面BCC1B1的交线长的最大值为[CD#4].

【答案】π．

【解析】如图11，取B1C1的中点为E，因为∠BAD=60°，直四棱柱ABCD-A1B1C1D1的棱长均为2，所以△D1B1C1为等边三角形，所以D1E=3，D1E⊥B1C1，又四棱柱ABCD-A1B1C1D1为直四棱柱，所以BB1⊥平面A1B1C1D1，所以BB1⊥D1E，因为BB1∩B1C1=B1，所以D1E⊥侧面B1C1CB.设P为侧面B1C1CB与球面的交线上的点，则D1E⊥EP，因为球的半径为R，D1E=3，所以

[JB（｜]EP[JB）｜]=[JB（｜]D1P[JB）｜]2-[JB（｜]D1E[JB）｜]2=R2-3，所以侧面B1C1CB与球面的交线是扇形EFG的弧，根据弧长公式f（R）=[JB（｜]α[JB）｜]rr=[JB（|]EP[JB）|]=R2-3得：

f（R）=πR2-3，3≤R≤2

π-2arccos1R2-3R2-3，2≤R≤7

2π2-arccos1R2-3-arccos2R2-3R2-3，7

由此，原高考題中R=5时，代入得f5=22π．

当3≤R≤22时，侧面B1C1CB与球面的交线变化过程的平面图如图12，由上面的函数关系式可知，当R=2时，f（R）max=f（2）=π.f（R）∈［0，π］.对应的函数图像如下图13．

除了选择、填空题外，以正方体为载体的大题也在高考数学中出现过，如2021年全国高考数学北京卷第17大题，2020年全国高考数学北京卷第16大题等，这些留给读者后面仔细去品味了．

正方体是日常生活中最常见、最熟悉的几何图形，涵含着丰富的空间元素与空间想象，是考查空间想象能力的绝好载体！些题又一次再现了命题人的“摘叶飞花”的功夫与“大道至简”的道理，抓住了数学的本与源，根和魂.正可谓：方中有数，平淡为真．

责任编辑 徐国坚