源于定位且高于定位的坐标系

2023-05-25龚辉

初中生世界 2023年23期

文／龚辉

几何始于土地丈量，研究的是图形，与代数的发展仿佛是两条平行线。笛卡尔这位大咖的登场，让我们迎来几何与代数完美结合的高光时刻。

笛卡尔发明了坐标系，用这把金钥匙开启了解析几何的大门。据传说，笛卡尔发明坐标系源于墙角的蜘蛛结网，而现在，电影院里的几排几座、地理上的经纬定位等，都有坐标系的身影。其实，我国早在西晋时期，裴秀主编的《禹贡地域图》中，就讲述绘制地图的六项原则，即著名的“制图六体”。可见当时我国的定位技术已经非常成熟，但可惜裴秀没有再深入一步形成坐标系，否则那可要比笛卡尔还早1300多年呢。

下面我们结合几道题目，看看笛卡尔的坐标系给我们的几何学习提供多少便捷的方法。

一、动点问题与数轴

数轴的本质是一条动了“手脚”的直线，有原点、正方向和单位长度。正是这三个元素，让这条不起眼的直线得以超凡脱俗，成为一维空间上数形结合的利器。

例1 如图1，A、B两点间的距离为12cm，点P从点A出发以2cm/s 的速度由A→B→A运动，同时，点Q从点B出发以1cm/s 的速度由B→A运动，当点Q到达点A时P、Q两点停止运动，设运动时间为t（s）。当t的值为多少时，点P与点Q相距3cm？

图1

【思路分析】动点问题是我们学习的难点，也是常见的考点。如果把线段AB放在数轴上，就可以将点与数建立起一一对应的关系，再利用数轴上两个点之间距离的规律（公式），就可以很方便地得到方程，从而得解。

在将线段放置在数轴上的时候，以对称的方法把AB的中点放在数轴的原点O处，可以简化运算（如图2）。

图2

我们可以将各个点所代表的数用数字或字母一一表示出来：A表示-6，B表示6，Q表示6-t，P到达点B前为-6+2t，到达点B后为6-（2t-12）。则当点P到达点B前，若两点相距3cm，可得方程（|6 -t）-（- 6 + 2t）|=3，解得t=3，t=5；当点P从点B返回时，可得方程（|6 -t）-（18 - 2t）|=3，解得t=9，t=15（因为返回时6＜t≤12，故t=15 舍去）。综上所述，当t的值为3、5、9时，点P与点Q相距3cm。

【反思点评】从几何角度解决这个问题需要观察各线段之间的数量关系，当线段有重叠和交错时，往往会影响我们做出正确判断。同时，两点相距3cm，需要对相遇前和相遇后分情况讨论，情况较为复杂。但是，如果将图形放置到数轴上，每个点赋予一个数，则可以利用A（a）、B（b）两点间距离为||a-b解决。引入绝对值可以有效规避上述分类讨论。

二、翻折问题与坐标系

将两条数轴按一定的规则放置便构成了坐标系，这是二维空间内数形结合的利器。下面我们来看看建立合适的坐标系在解决较复杂几何问题方面的强大功效。

例2 如图3，点O为矩形ABCD的对称中心，AB=10cm，BC=12cm。点E、F分别从A、B两点同时出发，沿矩形的边按逆时针方向匀速运动，点E的运动速度为1cm/s，点F的运动速度为3cm/s。当点F到达点C时，点E随之停止运动。在运动过程中，△EBF关于直线EF的对称图形是△EB′F，设点E、F运动的时间为t（单位：s）。是否存在实数t，使得点B′与点O重合？若存在，求出t的值；若不存在，请说明理由。

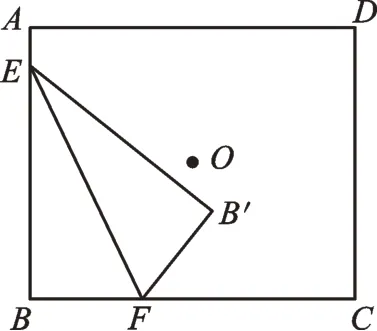
图3

【思路分析】这是一道苏州市中考压轴题的改编题。本题既有动点又有翻折，设问的形式为“是否存在”，具有一定的难度。如果将矩形放置在平面直角坐标系内，赋予各点以坐标，将几何关系转化为代数运算，可以较轻松地解决问题。

建立如图4 所示的坐标系：点B为原点，BC和AB所在直线为x轴、y轴。假设点B′与点O重合，由题意可得B′（6，5）。连接BB′，交EF于点H，由折叠可得EF垂直平分BB′，且H（3，2.5）。可得直线EF的表达式为y=-1.2x+6.1，则EF与两轴的交点为0）。故矛盾，即点B′不可能与点O重合。