溯本“清源”回归“本源”

文／ 张晓东

专题复习 图形的变化 图形与坐标

领衔人：龚 辉

组稿团队：江苏省太仓市高新区中学

图形的变化是初中几何的重要内容，主要包括图形的平移、翻折和旋转等。在学习中，如果我们对各种图形变化的“本源”理解不到位，对不同图形变化之间的区别与联系认识不清楚，会给我们应用图形变化知识解决问题带来偏差甚至错误。下面就以几道典型例题和大家一起剖析，期待对同学们的学习有所帮助。

一、概念“本源”理解不清晰

例1 如图1，已知AC是矩形纸片ABCD的对角线，AB=3，BC=4。现将矩形ABCD沿对角线AC剪开，再把△ABC沿着AD方向平移，得到图2 中△A′BC′，当四边形A′ECF是菱形时，平移距离是_____。

图1

图2

【易混点】本题是平移背景下求线段长度问题。很多同学能够根据“四边形A′ECF是菱形”这一条件求出相关线段长度，但如果对平移距离的概念理解不清晰便会出现错误。

二、性质“本源”掌握不牢固

例2 如图3，Rt△ABC中，∠B=90°，AB=3，BC=4。将△ABC绕点A旋转得到△ADE，且点D恰好落在AC上，连接EC，则sin∠DCE的值为（）。

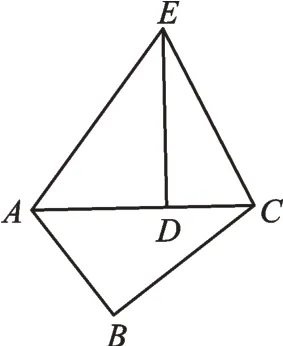
图3

【易混点】有的同学在观察图形后得∠DCE=∠BAC，然后通过计算得sin∠DCE=。错解的产生，一是缺少严密的逻辑推理，仅从直观感受得到结果；二是对旋转变化的性质掌握不牢固。

【解析】在Rt△ABC中，得到AC=5。根据旋转性质可得AE=5，AD=3，DE=4，所以DC=2。最后，在Rt△EDC中，利用勾股定理可求得EC=，从而求出sin∠DCE=。

三、变化过程“本源”分析不透彻

例3 如图4，有一张矩形纸条ABCD，AB=5cm，BC=2cm，点M、N分别在边AB、CD上，CN=1cm。现将四边形BCNM沿MN折叠，使点B、C分别落在点B′、C′上。在点M从点A运动到点B的过程中，若边MB′与边CD交于点E，则点E相应运动的路径长为cm。

图4

图5

【易混点】在点M的运动过程中，除了图5（点M与点A重合）和图6（MB′⊥AB）两个特殊情形外，还有一种特殊情形是点B′落在DC上，对图形变化过程分析不透彻就很容易漏掉。

图6

图7

四、题意“本源”运用不到位

例4 如图8，点A的坐标为（0，2），点B是x轴正半轴上的一点，将线段AB绕点A按逆时针方向旋转60°得到线段AC。若点C的坐标为（m，3），则m的值为（）。

图8

图9

【易混点】对于旋转90°，很多同学容易想到构造“K”字型解决问题。但此题是旋转60°，有的同学无从下手，随意猜测答案。

【解析】本题以平面直角坐标系为背景设置问题，同学们解读题意时要充分利用旋转60°的条件，由“线段旋转60°”联想“等边三角形”，而等边三角形的性质是解题的纽带。故可以连接BC，过点C分别作CD⊥y轴，CE⊥x轴，垂足分别为D、E，如图9。易证四边形CDOE是矩形，所以CD=m，CE=3，AO=2，AD=1。设OB=x，则BE=m-x，分别在Rt△AOB、Rt△ACD、Rt△BCE中，由勾股定理可得AB2=4+x2，AC2=1+m2，BC2=（m-x）2+9。又因为△ABC为等边三角形，所以AB=AC=BC，所以AB2=AC2=BC2，即4+x2=1+m2=（m-x）2+9，消去x，整理得3m4-22m2-25=0，解得