基于戴明回归和ROI细化的指针式仪表读数技术

徐小强, 陈 旭, 冒 燕

(武汉理工大学 自动化学院, 湖北 武汉 430070)

指针式仪表的示数读取主要分为表盘识别、指针提取和示数计算3个步骤.表盘识别一般使用霍夫圆检测[1]、椭圆检测[2-4]和深度学习[5-6]等方法;指针提取则普遍采用霍夫直线检测[1,7-9]、最小二乘法拟合[4,10]和剪影法[11-12]等方法;示数计算最为常用的是距离法[8,13]和角度法[1,4,9,12,14]两种.3个步骤中又以指针提取最为关键,目前最有效的算法是霍夫直线检测,但是进行霍夫直线检测需要将图像细化,会消耗大量时间,并且很容易受到背景或其他因素的影响导致精度降低.ZHU J.T.等[4]试图使用最小二乘法拟合直线代替霍夫直线检测以提高速度,但最小二乘法拟合直线也很容易受到背景因素的干扰,并且最小二乘法只考虑单一方向上的误差,仍然会导致读取结果的偏差较大.LI P.F.等[15]提出一种8特殊点标注法,首先对模板图像进行标注,再根据标注信息在表盘圆环带中定位指针位置;该方法对指针的定位精度高,但是其用到的模板图像需要人为标定.ZHANG Y.Q.等[10]提出一种基于模板匹配和动态TMLP的方法对指针进行定位,再使用最小二乘法拟合指针偏转角度和仪表示数的关系,可以消除同型号仪表中因不同仪表之间的微小差异而引起的误差,但是算法复杂度高,计算速度慢.

为解决上述问题,文中拟提出一种基于戴明回归和感兴趣区域(region of interest,ROI)细化的方法来读取指针式仪表示数.首先使用mask(掩膜)技术对图像处理,选出ROI,在ROI中锁定指针后取其外接矩形作为进一步缩小的ROI;然后在原图上锁定这一小区域,对此小区域使用细化算法细化;最后使用戴明回归对指针所在直线进行拟合,在此过程中利用帧差法消除指针抖动的影响.得到指针直线后获取斜率,再利用角度法计算出仪表数值.

1 仪表示数读取算法流程

文中提出一种基于戴明回归和ROI细化的指针式仪表示数读取技术,适用于指针式仪表示数的自动读取.该方法的实现流程如图1所示.

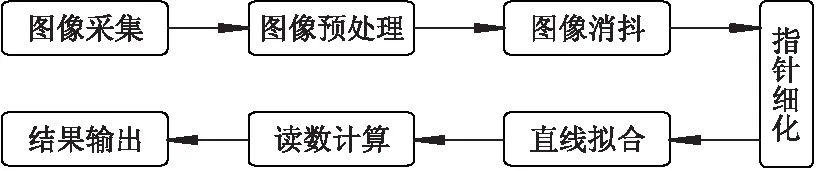
图1 示数读取流程示意图

使用摄像头采集指针式仪表的图像时,常常包含复杂的背景信息和噪声,这会影响指针识别的精度[9],所以在检测指针之前需要对图像进行预处理,消除干扰.ROI的选择是识别过程中的重要部分,它直接影响指针区域识别的效果.在拟合指针所在直线的方程之前,需要对指针区域图像做细化处理,以增加直线的拟合效果.使用戴明回归拟合直线并计算直线方程.最后根据拟合出的直线的斜率计算角度,利用角度法计算出仪表当前的示数.

2 算法设计

2.1 图像预处理

2.1.1选择ROI

在获取的图像中,不仅有仪表本身所带的背景图像,还有仪表所处环境的背景图像,这些信息会对指针提取造成影响.利用mask技术可以将背景变成黑色,进而突出选定的ROI.在指针识别过程中,指针的活动区域为如图2所示的绿色环形带,在指针活动的区域内选定ROI为如图2所示的蓝色环形带.

图2 指针活动区域示意图

2.1.2基于颜色通道的剪影法

提取指针需要用到剪影法,但是普通的剪影法需要获取仪表的无指针图像,计算式为

P(i,j)=I(i,j)-N(i,j),

(1)

式中:P(i,j)、I(i,j)、N(i,j)分别表示指针图像、待识别图像、无指针图像的像素值.

改进的剪影法利用指针的颜色信息,将图像分为R、G、B共3个通道,根据指针颜色的高区分度对3个通道进行加减运算即可提取出指针的颜色信息.试验中使用的仪表指针为红色,利用改进的剪影法提取指针信息,计算式为

P(i,j)=G(i,j)-R(i,j),

(2)

式中:G(i,j)、R(i,j)分别为原图像G、R通道的像素值.需要说明的是根据指针颜色信息的不同,3个颜色通道之间的运算式需要进行相应的调整.

2.1.3二值化和形态学操作

利用基于颜色通道的剪影法对选定的ROI处理之后,ROI内的像素值分布于0～255,虽然此时仪表的指针和背景具有一定的区分度,但是还需要利用二值化技术进一步处理,为二值化选定适合的阈值之后,使ROI内像素值设置为0或255.

形态学操作是图像处理过程中经常会用到的方法,其基本运算包括膨胀、腐蚀、开、闭、顶帽和黑帽等.使用膨胀操作可以修复二值图像中的小型黑洞,增加二值化图像的连通性.

2.2 图像消抖和ROI细化算法

仪表的质量有好有坏,即使是同一厂家同一批次生产的仪表质量也会有差异,而仪表所测量的设备稳定性也不尽相同,再加上一些不可控的外界因素,都会使测量时指针发生轻微的抖动.在提取指针和计算示数之前如果不消除此类影响,会导致读取结果不稳定.

当仪表指针稳定在某一刻度不发生变化,或者只有很轻微的抖动时,可以认为当前仪表的示数没有改变,直接使用前一张的结果,减少计算量.

针对上述问题,对指针图像做消抖处理.对前一张图像处理之后,将其二值化图像保存,与当前张的二值化图像做按位异或,计算二者之间的差异,若差异小于某一阈值,则说明当前图像中指针位置稳定不变或者仅存在抖动,直接输出前一张图像的处理结果即可.计算式为

(3)

式中:P(i,j)、Pb(i,j)分别表示当前张、前一张的图像像素值;D表示两张图像异或操作之后得到的差异值;⊕表示异或操作.

在消抖的过程中阈值的选择尤为重要,若选的太大会造成读数不灵敏,误将实际的指针变化判别为抖动,若太小则起不到消抖的效果.文中选取阈值的计算式为

(4)

(5)

式中:Vmax、Vmin分别为量程上限、下限;R是人为选取的最小分辨率,一般选择为待识别仪表刻度最小分辨率的十分之一;D(k,k+1)表示仪表指针移动k+1个分辨率之后的二值化图像和移动k个分辨率后的二值化图像按位异或之后得到的差异值.

排除了抖动的影响,拿到待识别图像的ROI,需要对ROI图像做细化处理.细化也称骨骼化,需要注意4点要求:保留源图像的连通性;保留端点和孤立点;对称细化;保证算法各向同性.

常用的细化算法有Zhang快速并行细化算法、Deutch细化算法、Hilditch细化算法和Rosenfeld算法.文中选用Rosenfeld算法细化指针,但稍作修改,在执行细化算法之前,将图像边界处的像素值全部置零,消除边界值邻域点的特殊情况给指针细化带来的影响.

在Rosenfeld算法中最重要的是连通域的概念,选择目标点周围8个邻域点构成8个连通区域.在Rosenfeld算法中,将删除后不会改变连通性的目标点称为8simple点.如图3a、b所示分别为非8simple点和8simple点.

图3 目标点分类图

Rosenfeld算法会删除是8simple点但不是孤立点(outlier)和端点(endpoint)的像素点.如果目标点周围8个点的像素值之和为0,则此目标点为孤立点;如果目标点周围8个点的像素值之和为1,则此目标点为端点.

Rosenfeld算法的迭代过程如下:① 逐个扫描所有像素,如果某像素是上边界点、下边界点、左边界点或者右边界点,且是8simple点,但不是孤立点和端点,删除该像素;② 重复步骤①直到没有目标点可被删除,退出循环.

2.3 基于戴明回归的直线拟合算法

细化后的指针图像中白色像素点组成的直线就是指针所在的直线,为拟合出该直线的方程,普遍使用的方法是霍夫直线检测,但是这种方法要求搜寻的直线经过的特征点最多,在实际使用过程中,指针所在直线不一定是经过特征点最多的那一条,而是所有的特征点都在指针所在直线的附近.

此时虽然可以使用最小二乘法拟合直线解决这一问题,但是最小二乘法拟合直线只考虑到y方向上的误差,具有不合理性.

所以文中选择使用戴明回归拟合仪表指针所在直线,戴明回归拟合直线与最小二乘法拟合直线的原理一样,但是它们需要优化的目标函数不同,可以通过优化函数,使得所有特征点到目标直线的斜距离最短.

求出特征点(x,y)的样本均值为

(6)

求出特征点(x,y)的样本方差为

(7)

求出x和y的协方差为

(8)

设目标直线为

(9)

则利用戴明回归拟合直线方程时,待优化的目标函数为

(10)

(11)

2.4 基于角度法的仪表示数计算

通过戴明回归拟合出指针所在直线,即可得到直线斜率,再利用斜率计算指针的偏转角度.此时需要注意的是如果指针的偏转角度大于90°,计算所得的角度会比实际角度滞后半个函数周期,需要将该角度加上180°.

得到指针偏转角度后,根据仪表盘刻度情况将其转化为仪表示数.首先根据先验知识获取仪表盘中指针指向最小刻度线和最大刻度时的指针偏转角度θmin和θmax,仪表示数计算式为

(12)

3 试验结果与分析

3.1 试验设计

为了验证文中方法的可行性,设计了试验.试验硬件装置包括0～30 V直流电压表、0～30 V直流电压源、计算机、USB高清摄像头、摄像头支架和试验台.首先固定电压表,将直流电压源与电压表连接,通过摄像头支架将摄像头固定使摄像头光轴与电压表平面垂直,使用计算机控制摄像头读取图像并读取电压表示数.计算机安装Windows10系统,使用Python编程.

具体试验方案如下:① 调节直流电压源输出恒定电压值,摄像头拍摄指针式仪表的图像,分别使用文中算法和霍夫直线检测的算法读取仪表示数,对比测试文中算法的识别精度;② 利用摄像头读取1 000张图像,利用等距抽样法选取80张图像,分别使用文中算法和全局细化算法进行处理,计算总时间和处理一张图像的平均时间,以测试文中算法的速度;③ 利用摄像头读取1 000张图像,选取其中连续的80张图像,计算总时间和处理一张图像的平均时间,与步骤②对比,测试文中提出的方法是否具有防抖动能力.

3.2 识别精度测试

为测试文中方法读取电压值的精度,将直流稳压电源的输出电压设置为5～20 V的16个整数电压值,通过摄像头获取仪表图像后,分别利用文中方法和霍夫直线检测方法对仪表示数进行读取.读取结果如表1所示,两种方法的误差曲线如图4所示.

图4 示数读取误差曲线

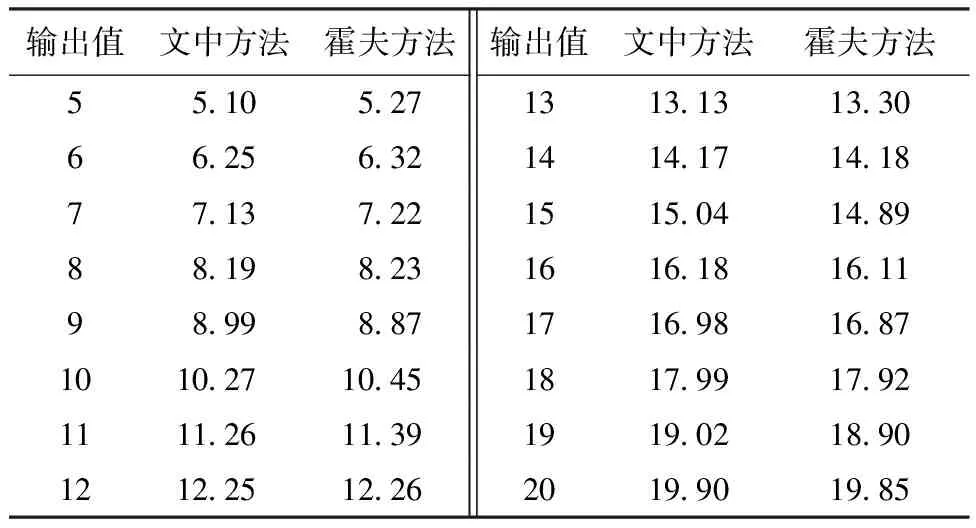
表1 电压读取结果对比 V

由表1可见,利用文中方法、霍夫直线检测方法读取仪表示数的平均误差分别为0.133、0.214 V,前者比后者减小了37.85%,可见文中提出指针识别方法的效果明显优于霍夫直线检测.

3.3 识别速度测试

为测试文中方法的计算速度,先利用摄像头读取1 000张大小为1 920×1 080像素的待识别仪表图像,再使用等距抽样法从1 000张图像中选取80张图像,利用文中方法(未加入防抖功能)连续处理选取到的图像,计算总时间和每张图像处理的平均时间,并与利用全局细化处理图像的时间对比,对比结果如表2所示.

表2 计算时间对比 s

由表2可见,对一张1 920×1 080像素的图像进行全局细化处理,需要193.375 s,而使用文中的ROI细化算法处理,只需0.658 s.试验结果表明,文中方法对每张图像的平均计算时间较常规的全局细化算法减少了192.717 s,可见文中方法在计算速度方面有了很大的提升.

3.4 防抖能力测试

为测试文中方法的防抖能力,利用摄像头读取1 000张大小为1 920×1 080像素的图像,选取其中连续的80张图像,利用文中方法(加入防抖功能)处理图像,计算所用时间并与3.3节中的结果做对比,对比结果如表3所示.

表3 是否有防抖功能计算时间对比 s

由表3可见,文中算法加入防抖功能后的单张图像平均计算时间在未加防抖功能的基础上又减少了0.050 s,这说明在加入防抖功能之后,文中方法识别出了某几张图像是前一帧图像的抖动产生的,直接显示了前一帧图像的处理结果,因此节约了计算时间.

4 结 论

文中提出一种基于戴明回归和ROI细化的指针式仪表读数技术,该方法检测的平均误差比霍夫直线检测减小了37.85%,每张图像的平均计算时间比全局细化算法减少了192.717 s,同时具有防抖动能力.文中提出的方法适用于各种常规的指针式仪表,但是该方法没有加入表盘识别部分的内容,所以要求待识别仪表与摄像头位置相对固定,在之后的学习研究中,需要对表盘识别部分的内容加以完善.