基于RESO和复合滑模的永磁同步电动机调速控制

李 娟, 冯 波, 李生权, 王书旺, 哀 薇

(1.扬州大学 电气与能源动力工程学院, 江苏 扬州 225127; 2.华南理工大学 自动化科学与工程学院, 广东 广州 510641)

永磁同步电动机(permanent magnet synchronous motor,PMSM)因其具有体积小和高可靠性等优点被广泛应用在现代工业领域,尤其是高精度伺服系统场合[1-2].然而PMSM在实际运行过程中常常面临内部参数摄动、外部干扰等方面的影响,使得电动机的高性能调速受到影响,甚至导致控制系统趋于不稳定.PMSM调速系统普遍采用PI控制来实现,而传统的PI控制是单自由度控制,难以兼顾响应与抗干扰两方面的控制性能,因此在一些外界环境恶劣的情况下,PI控制器对PMSM的高性能调速效果并不理想.因此,开发有效的控制策略来提高永磁同步电动机的速度控制性能已成为近几十年来的热点问题.近年来,为了提高永磁同步电动机的速度控制性能,许多先进的控制算法被应用到电动机控制[3-4]中,其中自抗扰控制(active disturbance rejection control, ADRC)与滑模控制(sliding mode control, SMC)由于具备优良的动态性能受到研究者们的格外关注[5-7].此外,在实际运转中对电动机建模容易产生误差,而自抗扰控制技术不依赖系统模型,其中扩张状态观测器(extended state observer, ESO)用来估计总干扰和各阶状态变量,并在前馈通道对总干扰进行补偿,提高系统的动静态性能.文献[8]利用扩张状态观测器提取干扰信号并加以补偿,有效地抑制干扰,从而解决机电系统的位置跟随和速度响应问题.文献[9]针对时滞系统中ESO相位滞后的问题设计出降阶扩张状态观测器(reduced-order extended state observer, RESO),对比了线性扩张状态观测器与降阶扩张状态观测器在频域范围内的幅频特性、相位特性和抗干扰能力.滑模控制是一种具有很强抗干扰能力的非线性控制策略,尤其是对永磁同步电动机这种非线性系统具有良好的控制效果.文献[10]基于ESO和SMC,对控制系统中总干扰以及变量进行估计,提高五相永磁同步电动机的抗干扰能力和速度控制精度.文献[11]设计了变速指数趋近律函数的滑模控制,应用到PMSM调速系统中,并抑制系统运行时产生的干扰,提高系统的抗干扰能力.

文中针对永磁同步电动机存在参数变化、负载干扰等问题,拟提出基于RESO的复合滑模控制器,对永磁同步电动机速度环进行优化设计.由于电动机速度信号可以直接测量,在状态变量已知情况下,可以不采用状态观测器观测,从而设计出降阶状态观测器并结合滑模控制的复合控制器,并对该策略进行性能分析,与传统方案进行仿真和试验对比,以验证文中所提复合滑模控制器的稳定性和抗干扰能力.

1 PMSM的数学模型

文中采用表贴式永磁同步电动机作为研究对象,建立Odq坐标系下的电动机电压方程为

(1)

式中:ud、uq、id、iq、Ld、Lq分别为d、q轴定子电压、电流、电感;Rs为定子电阻;ωe为电角速度;ψf为永磁体磁链.PMSM在Odq坐标系下的电磁转矩方程为

(2)

式中:np为极对数.电动机的机械运动方程为

(3)

式中:Jn为转动惯量;B为阻尼系数;TL为负载转矩;ωm为机械角速度.

2 基于RESO和复合滑模转速控制器的设计

2.1 RESO的设计

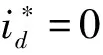
(4)

(5)

定义系统的状态变量x1=ωm,x2=a,则方程(5)的状态方程表示如下:

(6)

(7)

根据Luenberger状态观测器设计线性扩张观测器(linear extended state observer, LESO)如下:

(8)

式中:β1、β2是LESO的控制增益;Z=[z1z2]T,z1为状态变量ωm的估计值,z2为总干扰的观测值.进一步将式(8)展开,可得线性扩张状态观测器为

(9)

选取二阶扩张状态观测器的特征方程为

λ(s)=s2+β1s+β2.

(10)

设计理想特征方程为

λ(s)=(s+p)2.

(11)

则观测器控制增益为

(12)

(13)

定义新的状态变量为

(14)

(15)

将式(15)进行拉氏变换,得到系统的扩张状态观测量为

(16)

(17)

当观测器能够准确且快速地观测出系统总干扰的情况下,由式(5)和(17)可得

(18)

此时控制律u0选取及控制器输出量u设计如下:

(19)

式中:u是控制器的输出值即控制量iq.

2.2 复合滑模控制器设计

通常控制律中采用增大比例控制来提高速度环的动态性能,而纯比例控制无法有效地抑制高频干扰,甚至可能带来噪声,因此引入滑模控制来增强系统的抗干扰能力,并通过ESO解决滑模控制引起的抖振问题.文中采用基于RESO的复合滑模控制,其复合控制框图如图1所示.

图1 速度环复合控制结构图

对式(5)设计滑模控制器,定义跟踪误差为

e=ω*-ωm.

(20)

式中:ω*为给定输入速度.定义滑模面为

s=e.

(21)

对式(21)求导可得

(22)

选择指数趋近律为

(23)

式中:-εsgns是等速趋近项;s是滑模面;-ks是指数趋近项.针对系统方程(5),结合降阶扩张状态观测器设计复合控制律为

(24)

由于文中采用DSP芯片TMS320F28335为控制核心验证,则对式(15)进行离散化处理:

(25)

控制器离散化表达式为

(26)

3 速度环复合控制器性能分析

3.1 降阶扩张状态观测器的性能分析

根据式(5)和(9),得到LESO实际干扰和观测干扰的传递函数为

(27)

根据式(13)和(17)得到RESO实际干扰和观测干扰的传递函数为

(28)

选取的观测器带宽为p=1 000 Hz,得到时间响应曲线见图2,幅频相频特性曲线见图3.根据文中对象的实际情况,由图2可见在单位阶跃响应下,RESO比LESO具有更快的观测速度;由图3可见降维观测器相对于扩张状态观测器在低频段可以获得更好的估计性能.

图2 时间响应曲线图

图3 幅频和相频特性曲线图

3.2 稳定性分析

针对系统(17)对RESO进行稳定性分析.首先,定义RESO干扰估计误差为

(29)

对式(29)求导可得

(30)

选取Lyapunov函数

(31)

对式(31)进行求导,并将控制器(23)代入,可得

-ks2-η|s|<0.

(32)

4 系统验证

4.1 调速系统仿真及分析

为了验证速度环降阶扩张状态观测器的滑模复合控制性能,搭建PMSM调速系统模型,系统结构框图见图4.PMSM 参数如下:极对数np=4对;电阻Rs=0.165 5 Ω;线电感Ls=0.45 mH;磁链ψf=0.175 Wb;转动惯量J=0.003 kg·m2;额定功率P=200 W;额定转矩TN=0.637 N·m;额定电流IN=7.5 A;额定电压UN=36 V.

图4 系统结构框图

采用3种控制器做对比,设置固定步长0.001 s,电流限幅值7.5 A,电流环PI参数kp=2,ki=0.1;速度环PI参数为kp=0.5,ki=0.05;采用LADRC参数为p=1 000,b=4 700,h=5e-5,kp=3.8;采用基于RESO的复合滑模控制时参数为ε=0.1,k=10,其余参数如带宽、控制器增益、积分步长与LADRC相同.

在给定转速为500 r/min且空载的仿真情况下,基于RESO的复合滑模控制和LADRC、PI控制的转速和iq变化曲线如图5和图6所示.在恒定500 r/min情况下,在t=2.5 s时突加0.2 N·m负载,速度曲线和iq变化曲线如图7和图8所示.

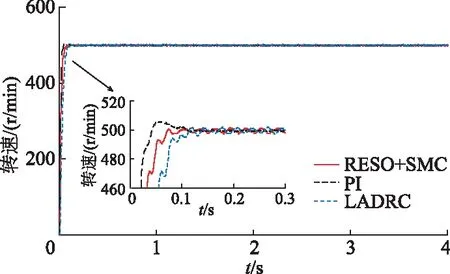
图5 转速响应仿真速度变化曲线

图6 转速响应仿真iq变化曲线

图7 负载仿真速度变化曲线

图8 负载仿真iq变化曲线

由图5可见,为了保证速度响应的快速性,PI控制通过牺牲超调来达到快速性效果,相比之下基于RESO的复合滑模控制和 LADRC控制转速响应曲线都不存在超调,且基于RESO的复合滑模控制控制响应时间更快,跟踪误差较小.由图6可见,基于RESO的复合滑模控制器具有较小的稳态误差,因此基于RESO的复合滑模控制器表现出更好的稳速性能.由图7和图8可见,基于RESO的复合滑模控制在响应速度和抗干扰能力方面均优于LADRC和PI控制.

4.2 调速系统半实物仿真平台搭建及功能验证

为了验证所提出的基于RESO和复合滑模控制方法的优越性,当在线仿真完成后,在MATLAB/SIMULINK环境下将模型代码自动生成到CCS,并直接下载到DSP(型号:TMS320F28335)进行通信.DSP用于对永磁同步电动机(型号:SM060R20B30MNAD)的转子角度信号和转速信号的采集和处理.然后将DSP产生的PWM信号传输到智能功率模块(IPM,型号:IRAM136-1061A),实现对永磁同步电动机的实时控制,联轴器用于连接永磁同步电动机与磁粉测功机(型号:GZC2)进行负载试验,智能功率模块的直流母线电压由直流电压恒流电源提供(型号:KX8010),DSP和智能功率模块的电源由开关电源提供(型号:S-100-24).由于在实际情况中调速系统存在许多不确定因素的影响,为达到最佳控制效果需要对仿真试验参数进行微调,建立永磁同步电动机系统的磁场定向矢量控制试验平台如图9所示.

图9 电动机系统矢量控制试验平台

在无干扰的速度响应试验中,转速按照0、500、1 000 r/min进行变速给定,速度环基于RESO和复合滑模控制、LADRC和PI控制器下的速度和q轴电流波形如图10和图11所示.

图10 速度响应试验速度变化曲线

图11 速度响应试验iq变化曲线

在加载试验中,电动机转速给定 500 r/min 且在6 s时进行加载0.2 N·m,即30%负载的情况下稳定运行,此时基于RESO的滑模控制、LADRC控制和PI控制下的速度响应曲线和q轴电流波形如图12和图13所示.

图12 加载试验速度变化曲线

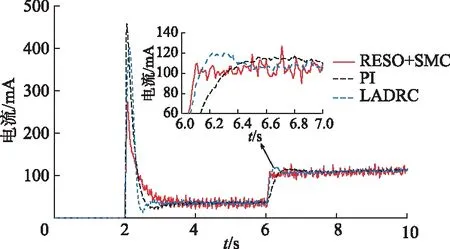
图13 加载试验iq变化曲线

由图10和图11可见,在0、500、1 000 r/min速度响应试验中,在到达指定转速后3种控制器都能保持稳速运行,而基于RESO的复合滑模控制在无超调和响应快的控制性能优于LADRC控制和PI控制,体现出更好的稳定性;在进行抗干扰试验中,采用磁粉制动器进行加载试验,由图12可见,在达到稳定转速后,基于RESO的滑模控制通过对PMSM调速系统总干扰的估计和补偿,加载干扰时转速动态速降为10 r/min,而LADRC控制和PI控制受到相同干扰后转速动态速降分别为30、50 r/min,所提出控制策略相较于上述两种算法转速变化量均减小60%以上;从而可知提出的控制方法跌落幅度更小,可以更加快速地调回到给定速度,与LADRC控制和PI控制对比所需要的调节时间更短并且速度上下的波动也更小,表现出较好的抗干扰能力.由图13可见,基于RESO的滑模控制2 s启动后转矩输出脉动现象明显被削弱,6 s加载后电流突变没有出现较大的波动以及超调,表现出更好的稳定性.由此可知,在PMSM调速控制系统中,基于RESO的复合滑模控制整体性能均更平稳,且响应速度更快,抗扰性能更强,改善了系统的稳定性.

5 结 论

文中构建了PMSM数学模型,并在调速系统中设计了基于RESO的复合滑模控制器.首先RESO相较于LESO具有更优越的观测速度和干扰估计性能;其次通过仿真与试验结果发现,基于RESO的复合滑模控制器与传统PI和LADRC控制器相比,在加30%负载情况下,转速变化量减少60%以上,可以有效抑制干扰,并显著提高系统的稳定性与动态响应.