无人驾驶汽车路面自适应MPC轨迹跟踪控制

郭 盼, 于蕾艳

(1.清华大学 机械工程系, 北京 100084; 2.中国石油大学(华东)机电工程学院, 山东 青岛 266580)

近年来,无人驾驶技术迅速发展[1],轨迹跟踪控制是热点问题[2-4].模型预测控制(model predictive control, MPC)算法广泛应用在车辆轨迹跟踪控制领域中.SONG P.等[5]基于模型预测控制设计了多约束控制器,与单约束控制器相比,车辆的侧向跟踪误差、航向角和侧偏角的变化表明车辆具有更好的轨迹跟踪控制性能.WANG H.Y.等[6]使用模糊控制算法自适应调节模型预测控制算法中目标函数的权重,和纯跟踪算法相比具有更优的控制能力.JI J.等[7]设计了一种基于模型预测控制的新型控制器,由环境感知模块和轨迹规划模块共同组成整个系统的决策模块,研究结果表明,控制器具有良好的轨迹规划和跟踪性能.H.KAZEMI等[8]建立了一种经过神经网络优化的模型预测控制器,应用在自适应巡航的场景下,在真实驾驶场景中评估控制器的性能,仿真结果表明,经过优化的控制器具有更优的控制性能.孙银健[9]在传统模型预测控制器的基础上增加了车辆动力学约束条件,研究了航向角、横摆角速度和质心侧偏角等评价指标随时间的变化,分析了在低附着系数道路上车辆的跟踪情况.胡家铭等[10]针对无人驾驶车辆存在的系统不确定性和外界干扰等问题,在模型预测控制器中引入反馈矫正机制来提高跟踪精度.刘凯等[11]基于零力矩点的车辆侧倾安全约束设计轨迹跟踪控制器,适应复杂越野地形,轨迹跟踪保证车辆安全性.

以上研究存在如下不足:① 只针对某几个特定的车速和道路附着系数工况进行研究,研究结果在全工况下不具有普遍性,无法代表车辆在全工况下的实际行驶情况;② 性能评价方法片面,无法准确全面地评价车辆在全工况下的轨迹跟踪精度和行驶安全性;③ 缺乏路面自适应控制,不能根据不同路面限制车速约束范围.

针对以上不足,笔者使用车辆3自由度非线性动力学模型,基于路面自适应模型预测控制方法,建立适合于全车速和全道路附着系数工况的无人驾驶汽车轨迹跟踪控制器.提出路径跟踪误差、侧向加速度、质心侧偏角、前轮侧偏角的最大值和标准差组成的评价体系,划分车辆全工况轨迹跟踪稳定区和失稳区,有助于探明无人驾驶汽车在全工况下的轨迹跟踪精度和行驶安全性.

1 车辆3自由度非线性动力学模型

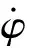
图1 车辆3自由度非线性动力学模型

车辆3自由度非线性运动微分方程为

(1)

式中:m为整车整备质量;Iz为绕z轴的转动惯量.

结合小角度假设和基于魔术公式轮胎模型线性化处理,由式(1)得车辆非线性动力学模型为

(2)

2 轨迹跟踪控制器设计

选用线控底盘作为轨迹跟踪控制的执行系统,线控转向子系统实现前轮转角的控制,线控制动子系统和线控驱动子系统实现车速的控制.全工况下基于模型预测控制的车辆轨迹跟踪原理如图2所示.

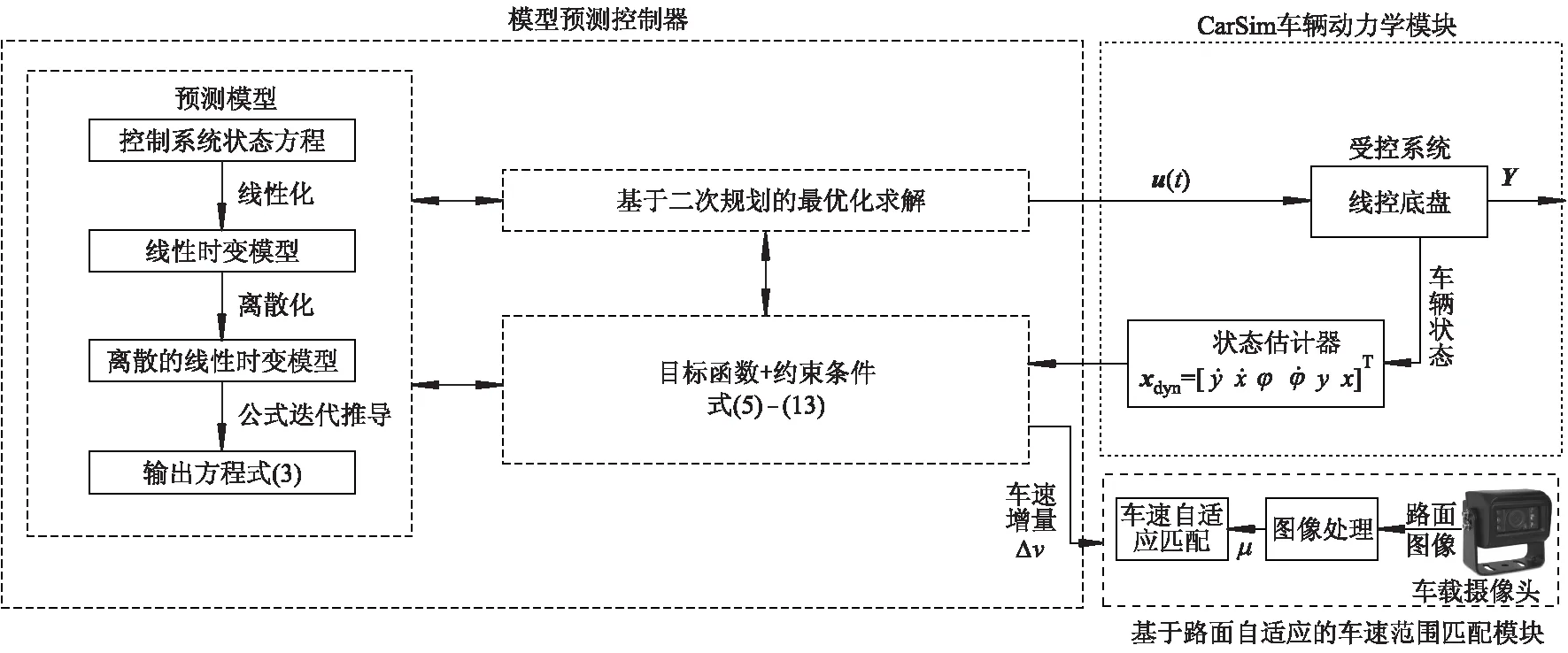
图2 全工况下基于模型预测控制的车辆轨迹跟踪原理

受控系统(无人驾驶汽车线控底盘)、模型预测控制器和状态估计器组成完整的模型预测控制系统.其中,模型预测控制器是在预测控制理论的预测模型、滚动优化和反馈校正[12]3个基本要素的基础上,结合约束条件、预测模型以及目标函数进行设计的.控制器结合约束条件不断对目标函数进行求解,计算得到控制变量序列u(t)后,其第1个值将会应用于受控系统,系统执行控制.状态估计器计算得到系统的状态量并反馈给控制器,不断更新预测模型.

1)预测模型.基于离散的线性时变模型,迭代推导出系统的输出方程为

Y=Ψξ(k)+ΘΔU,

(3)

式中:Y为输出向量;Ψ和Θ均为系数矩阵;ξ(k)为当前时刻的状态量;ΔU为控制增量向量.

由式(3)可知,若已知当前时刻的状态量ξ(k)和控制时域Nc内的控制增量ΔU,也就可以预测未来预测时域Np内的输出量Y,故将由式(3)作为控制系统的预测模型.

2)滚动优化.轨迹跟踪控制器在每个控制周期内要解决的优化问题归纳为

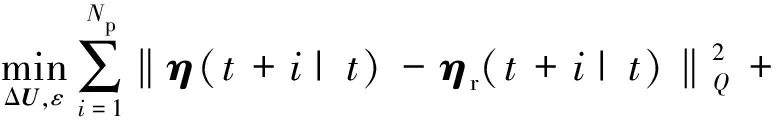
(4)

约束条件如下:

ΔUmin≤ΔU≤ΔUmax,

(5)

Umin≤AΔU+U≤Umax,

(6)

yhc,min≤yhc≤yhc,max,

(7)

ysc,min-ε≤ysc≤ysc,max+ε,

(8)

ε>0,

(9)

-12°<β<12°,良好路面,

(10)

-2°<β<2°,冰雪路面,

(11)

(12)

-2.5°<αf<2.5°,

(13)

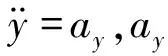
以上多约束条件中,式(10)和(11)约束了质心侧偏角;式(12)约束了侧向加速度;式(13)约束了前轮侧偏角,保证了车辆的行驶安全性.式(5)约束了车速和前轮转角增量,图2中的基于路面自适应的车速范围匹配模块中,车载摄像头检测的前方道路图像输送给CPU,结合神经网络等智能算法进行图像处理,估计出前方道路的附着系数.根据不同的道路附着系数,实现车速的自适应匹配,计算得到车速增量Δv.车速增量输送到模型预测控制器的约束条件中参与优化模型的最优化求解.

3)反馈矫正.在系统的每个控制周期中求解式(5)-(13)后,将获得受控系统在控制时域Nc中的一系列控制输入增量:

(14)

把获得的控制输入增量序列中的第1个元素作为实际控制输入增量应用于系统,从而获得最佳控制量:

u(t)=u(t-1)+Δut.

(15)

此时,系统将执行此控制量直到下一个时刻.在新时刻,系统将根据当前状态信息预测下一时刻的输出,并通过优化求解过程得到新的最佳控制增量序列,直到系统整个控制过程完成为止.

3 全工况轨迹跟踪效果分析

以全车速和全道路附着系数为例,研究无人驾驶汽车全工况轨迹跟踪精度和行驶安全性.融合CarSim和Matlab软件进行研究,基于模型预测控制的轨迹跟踪联合仿真模型如图3所示.

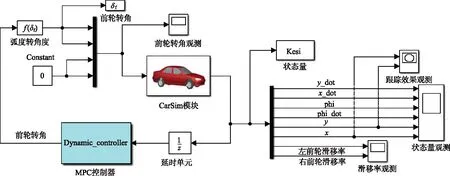
图3 基于模型预测控制的轨迹跟踪联合仿真模型

目标轨迹选用车辆行驶稳定性试验中广泛使用的双移线轨迹,其具有代表性和可重复性[13].车速v从10 m/s至30 m/s每隔5 m/s选取1个车速值,道路附着系数μ从0.1取至0.9,观察车辆在全车速工况以及全道路附着系数工况下的轨迹跟踪情况和稳定性.采用的评价指标中,路径跟踪误差表征轨迹跟踪精度,侧向加速度、质心侧偏角和前轮侧偏角表征行驶安全性.指标最大值表征车辆行驶经过大曲率路段时轨迹跟踪精度和行驶安全性的极限情况,标准差表征这些指标相对平均值的离散程度,反映车辆在整个轨迹跟踪过程中的性能波动情况.路径跟踪误差的变化规律如图4所示,其中:esmax为路径跟踪误差最大值;σs为路径跟踪误差标准差.

图4 路径跟踪误差的变化规律

从图4可以看出:车辆以低速在道路附着系数高的良好路面上行驶时,路径跟踪误差偏低,轨迹跟踪效果最好;当道路附着系数接近0.1时,5种车速下路径跟踪误差的最大值都偏大,甚至接近5 m;车速越低则越能够适应道路附着系数较低的路面,即车辆能够以低速在道路附着系数较低的湿滑路面上跟踪目标轨迹.车辆以10 m/s的车速行驶在道路附着系数为0.2的路面上时,路径跟踪误差最大值就已经降到低于1 m,而车辆以20 m/s的车速行驶在道路附着系数为0.7的路面上时,路径跟踪误差最大值才降至低于1 m.当车辆以25、30 m/s等高速跟踪目标轨迹时,即使行驶在道路附着系数为0.7或者0.8的良好路面上,路径跟踪误差最大值依然比较大,接近3 m,说明车辆在转弯处的轨迹跟踪效果差.

从图4c可以看出:车辆以低速行驶在道路附着系数高的路面上时,路径跟踪误差的标准差则比较小,说明车辆在轨迹跟踪过程中,其路径跟踪误差相对其平均值的离散程度更小,路径跟踪误差变化不大,跟踪效果较好.

侧向加速度的变化规律如图5所示,其中:aymax为侧向加速度最大值;σay为侧向加速度标准差.

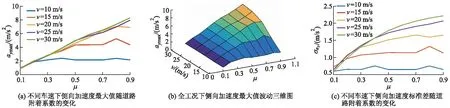
图5 侧向加速度的变化规律

从图5可以看出:当车辆以25、30 m/s等高速跟踪目标轨迹时,即使行驶在道路附着系数为0.7或者0.8的良好路面上,侧向加速度的最大值较大,接近7 m/s2.侧向力较大,车辆的操纵稳定性较差,所以在轨迹跟踪过程中要避免选择高速行驶;当道路附着系数接近0.1时,5种车速下的侧向加速度最大值均很小,接近0.1 m/s2,此时车辆的侧向附着力较小,侧向稳定性较弱,所以车辆的转向能力受到很大的影响,导致轨迹跟踪效果差;当道路附着系数逐渐升高时,侧向加速度最大值也随之增大,车辆的侧向附着力逐渐增大,侧向稳定性逐渐增强,车辆的转向能力也会随之变好,所以随着道路附着系数的提升,路径跟踪误差最大值也会迅速下降,由图4可知,最低能降到接近0.5 m,轨迹跟踪效果较好.

质心侧偏角的变化规律如图6所示,其中:αmax为质心侧偏角最大值;σα为质心侧偏角标准差.

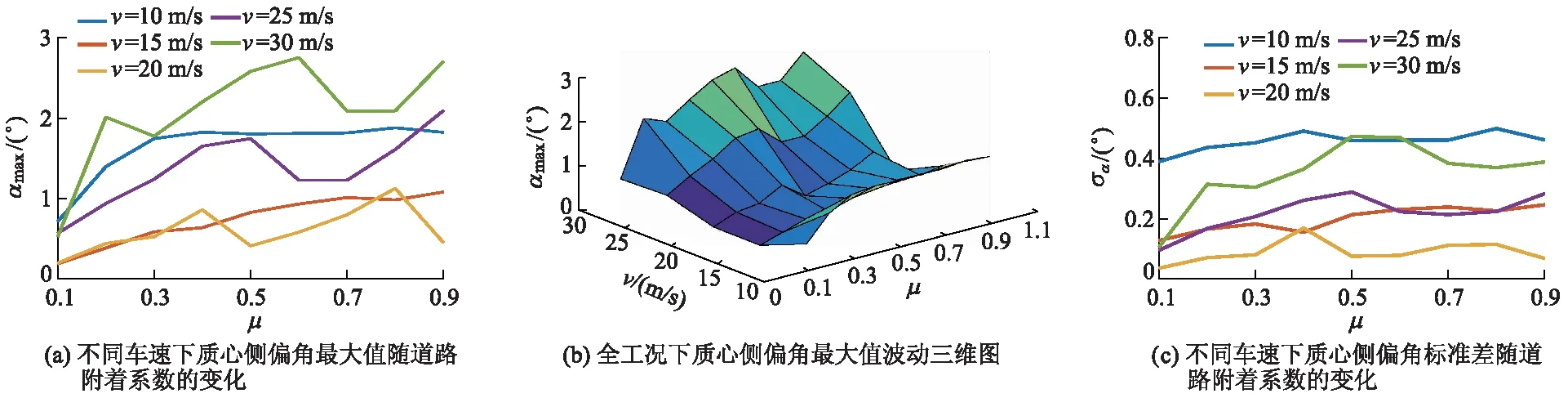
图6 质心侧偏角的变化规律

从图6可以看出:当道路附着系数为0.1～0.4时,车辆质心侧偏角满足约束范围(-2°, 2°);当道路附着系数为0.5～0.9时,车辆质心侧偏角满足约束范围(-12°, 12°),汽车的行驶安全性有保障.

前轮侧偏角的变化规律如图7所示.其中:αfmax为前轮侧偏角最大值;σαf为前轮侧偏角标准差.从图7a、b可以看出:车辆以10 m/s的车速行驶在道路附着系数大于0.3的路面上时,前轮侧偏角最大值低于3°,车轮的侧偏特性处于线性区域内;而车辆以15 m/s的车速行驶在道路附着系数大于0.5的路面上时,前轮侧偏角最大值低于3°,车轮的侧偏特性处于线性区域内;车速大于20 m/s时,无论道路附着系数如何变化,前轮侧偏角最大值均高于3°,车轮的侧偏特性均处于非线性区域内.这说明车辆以大于20 m/s的车速行驶经过50、100 m处的急弯时,车轮的侧偏特性处于非线性区域内,此时轮胎产生的侧向力逐渐趋于饱和,车辆的转向特性将会发生变化,从而导致侧滑等危险的发生.另外,当车轮的侧偏特性处于非线性区域时,驾驶员难以根据驾驶经验准确地操纵转向盘,控制车辆的行驶方向,极易发生交通事故.从图7c可以看出:车辆低速行驶在道路附着系数高的路面上时,前轮侧偏角的标准差则比较小,说明车辆在轨迹跟踪过程中,其前轮侧偏角相对其平均值的离散程度更小,车辆的行驶稳定性变化不大.为了保证车辆在轨迹跟踪的过程中既保证跟踪效果,又维持其行驶稳定性与安全性,有必要安装ESP(electronic stability program)等车辆稳定性系统.

图7 前轮侧偏角的变化规律

为了获得良好的轨迹跟踪精度和行驶安全性,考虑车速和道路附着系数的匹配关系,将车辆的行驶工况分割成如图8所示的2块区域:稳定区和失稳区.车辆在稳定区工况行驶时,车辆具有良好的轨迹跟踪精度和行驶安全性;车辆在失稳区工况行驶时,轨迹跟踪精度和行驶安全性会急剧恶化,这时就需要根据传感器检测到的路面信息及时调整车速的大小,重新回到稳定工况区行驶.

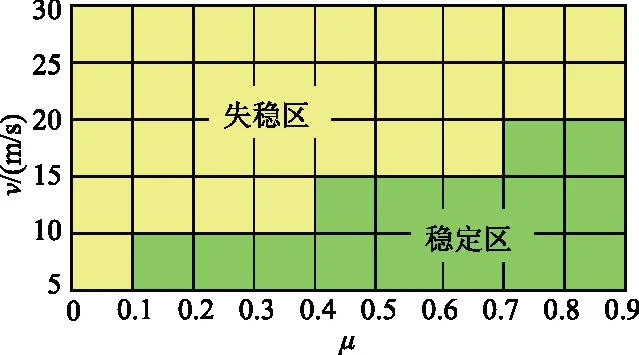
图8 车辆全工况轨迹跟踪稳定区和失稳区划分

4 结 论

1)在路面自适应模型预测控制器的设计中,结合车辆3自由度非线性动力学模型建立预测模型;制定车速约束条件时,根据传感器检测的道路附着系数进行路面自适应的车速范围匹配,提高在极限工况下的行驶安全性.

2)提出了路径跟踪误差、侧向加速度、质心侧偏角、前轮侧偏角的最大值和标准差组成的评价体系,准确评价全工况下轨迹跟踪精度和行驶安全性.

3)根据上述4个指标随着车速和道路附着系数的变化,分析了在全车速和全道路附着系数工况下的轨迹跟踪精度和行驶安全性,划分了车辆全工况轨迹跟踪稳定区和失稳区,为控制方法提供参考.

4)为了获得良好的轨迹跟踪精度和行驶安全性,需要根据车辆行驶工况匹配关系实时调节车速大小,使车辆始终保持在稳定区行驶,根据路面变化实现车速的自适应控制.

5)为了更全面地研究无人驾驶汽车在全工况下的轨迹跟踪控制,下一步研究引入对开路面等更丰富工况,拓展到融合时域和频域的综合研究.