基于菌群优化Spiking神经网络的渲染时间估计

胡 博,章 毅,蔡柳萍

(1.广东外语外贸大学 南国商学院,广东 广州,510440;2.湖南大学 环境科学与工程学院,湖南 长沙,410082;3.菲律宾圣保罗大学 研究生院,菲律宾 卡加延省土格加劳市,3500)

近年来,图像渲染在电影、动漫、雷达、遥感等多个领域得到了广泛应用[1]。虽然图像渲染给多个领域的复杂建模及图像增强带来新的机遇,但由于整个渲染编码过程需要强大的算力,对资源的消耗较大。一般都采用分布式或者集群方式来完成大规模的图像渲染[2]。分布式或集群式渲染任务的高效调度成为图像渲染大规模应用需要解决的重要难题。

在渲染任务的调度问题中最重要的设置参数就是渲染时间。若根据图像样本能提前预估样本的渲染时间,那么就能够根据不同任务的渲染时间来制定渲染调度策略,这将极大提升图像渲染效率。渲染时间的估计与渲染样本材质、几何特征、图像像素及灯光等多种因素有关,因此通过多种样本特征来进行渲染时间预估是一个十分复杂问题。

当前,关于图像渲染方面的研究较多,方杰[3]对WebGL平台的大规模渲染方式方法展开了研究,充分利用分布式计算优势来完成大量渲染编码工作。朱家敏等[4]采用小波变换进行图像渲染,重点解决了图像中的半透明渲染问题。两者研究都解决了特定应用场景的3D渲染技术问题,也提到了与渲染时间关系密切的图像样本特征,但在渲染时间方面并未展开深入研究。Dai等[5]提出了一种基于深度循环神经网络(Recurrent neural network,RNN)的物理渲染时间估计方法。Kallweit等[6]提出利用神经网络来预测大气云图像渲染的时间。从这两个研究文献可以看出,神经网络模型在渲染时间估计上具有较好的可行性。

但是,由于涉及多样本特征的提取和编码,基于神经网络(Neural network,NN)模型的渲染时间预估仍无法得到令人满足准确性和鲁棒性。作为一种新型的“第三代神经网络”,Spiking神经网络是神经网络研究领域的最新成果。相较于前两代神经网络,Spiking神经网络由于具有强大的计算能力常被广泛用于复杂问题的训练求解。Spiking神经网络通过脉冲信号实现数据的传递,根据脉冲点火时间来完成编码。相比于传统神经网络结构,Spiking神经网络训练具有更强的解决非线性预测或分类问题的能力。

由于深度卷积神经网络中的卷积编码层具有可学习性的优势,且编码方式更加灵活。因此,本文采用卷积Spiking神经网络(Convolutional Spike neural network,CSNN)来实现渲染时间估计,并采用菌群优化算法对CSNN参数进行优化求解,以进一步提高CSNN的渲染时间预估的准确性。

1 Spiking神经网络

1.1 基于Spiking的脉冲响应模型

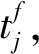
(1)

设所有前突神经元i均处于集合Γj中,点火脉冲对u(t)影响为

(2)

由以上得,后突神经元j的脉冲响应表示方法为

(3)

考虑到式(2)的计算复杂度,在实际使用时一般采用简化脉冲响应模型(SRM0)

(4)

突触电势εij(t)为[7]

(5)

式中：H(·)是阶跃响应,σ是常数。

1.2 卷积Spiking神经网络

基于Spiking的神经网络模型较多,本文选择了运算能力更强CSNN,以便解决复杂的最优求解问题。下面将对CSNN算法进行数学描述。

在CSNN运算中,需要先对样本特征进行Spiking采样,采样层第k层对应的第j个节点采样方法为[8]

(6)

式中：n为采样窗口尺寸,B为偏置。

经过采样的特征后进行卷积运算,Spiking卷积层第k层对应的第j个节点卷积运算方式[10]为

(8)

式(6)和(7)中的函数f一般设置[9]为

(7)

式中：T为编码函数,Kernel是卷积核,Mj为第j个特征图,B为偏置。

(9)

采用CSNN进行求解时,合理设置CSNN模型参数非常关键,这对CSNN模型的求解结果影响显著。实际应用求解时,由于样本差异,通过手动调参较为困难且性能不佳。因此本文考虑采用群体智能算法BFO对CSNN模型核心参数进行优化求解,以增强CSNN训练性能。

2 基于改进的Spiking神经网络渲染时间估计

2.1 菌群优化(BFO)算法

设菌群规模为S,其运动范围为[min,max],初始位置P[11]为

P=min+rand*(max-min)

(10)

式中：rand∈random(0,1)。

菌群个体的运动主要包含驱化、繁衍和迁徙3类操作。设细菌i的位置Xi=(x1,x2,…,xv),v表示位置维度,其从位置P经过第j次驱化后的位置[12]为

(11)

式中：C(i)为细菌i的驱化步长。

i经过驱化后的适应度[13]为

(12)

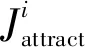
(13)

(14)

每进行一次驱化操作,便计算一次适应度,num次后,i的总适应度H(Xi)[15]为

(15)

根据适应度降序排列,选择较高的细菌个体进行繁衍操作,从而生成新的菌群位置。由于菌群的环境影响,细菌也可受环境改变而迁徙,从而改变菌群边界,因此经过繁衍和迁徙操作,都将生成新的菌群位置。

不断执行3种菌群运动方式,直到达到BFO停止条件。

2.2 渲染时间估计流程

首先提取3D图像样本的分辨率、几何面等关键参数,将所有参数进行归一化。根据渲染时间与3D模型参数之间的联系,然后建立CSNN渲染时间预测模型,将CSNN节点权重卷积核尺寸及偏置等参数构建菌群,接着通过菌群运动进行位置更新优化,以渲染时间预测准确率为适应度函数求解菌群最优个体,从而获得适合CSNN预测的最优参数,最后采用经过BFO优化后的CSNN进行预测。

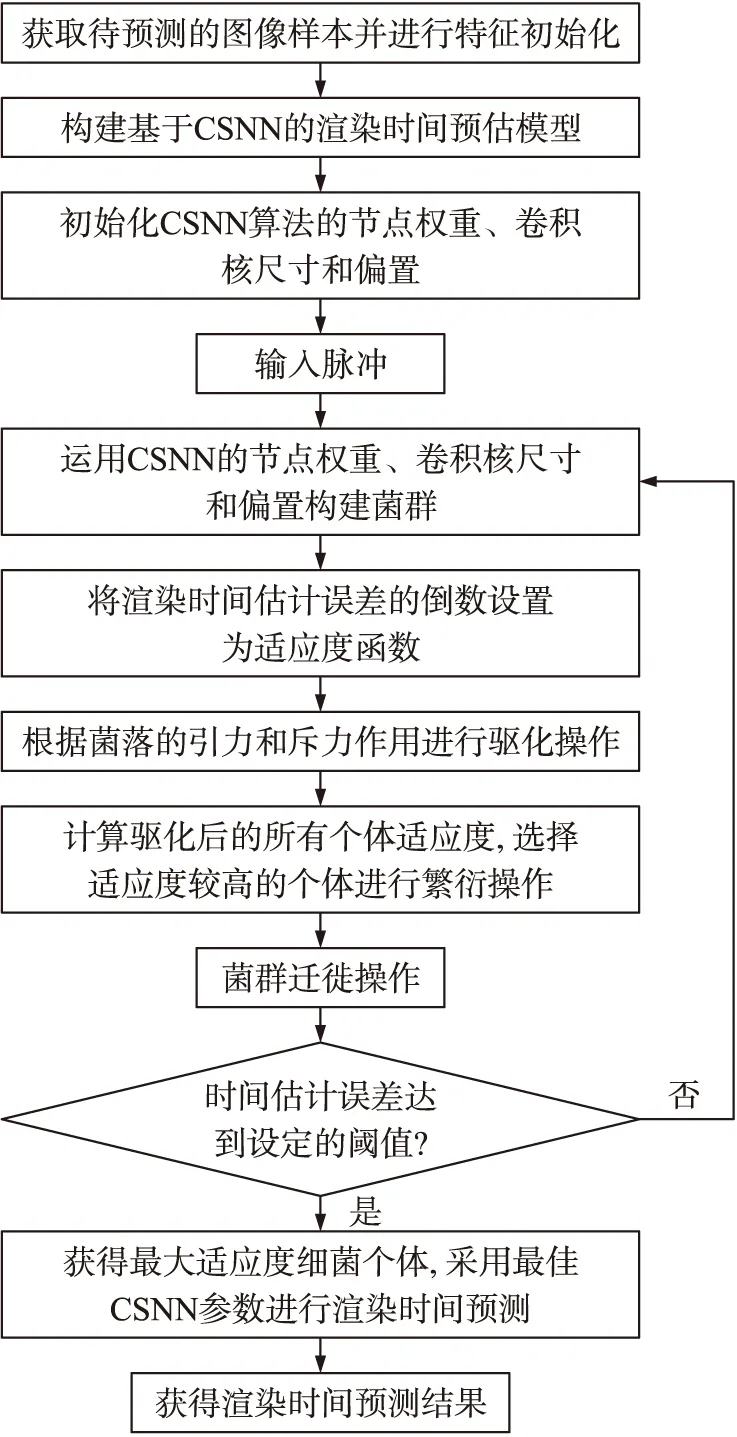
图1 基于BFO-CSNN的渲染时间估计流程

3 实例仿真结果与分析

为了验证BFO+CSNN算法对渲染时间估计的性能,进行实例仿真。渲染对象数据集为某3D动画样本,其数据集相关的样本特征如表1所示。首先,差异化选取不同菌群规模,采用BFO+CSNN算法进行渲染时间性能仿真,验证BFO+CSNN算法的预估性能;其次采用CSNN和BFO+CSNN算法分别对表1中的样本集进行渲染时间性能仿真,验证BFO对CSNN渲染时间预估的性能影响;最后采用BFO+常用神经网络算法和BFO+CSNN算法对表1样本集进行渲染时间进行性能对比。

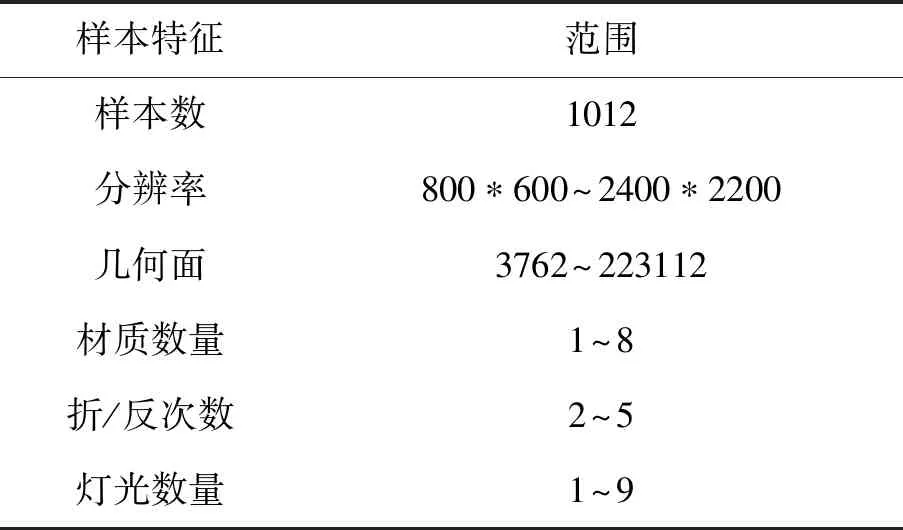
表1 仿真样本

渲染时间估计评价指标[16]主要为

(16)

(17)

(18)

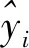
3.1 不同菌群规模的渲染时间预估性能

为了验证BFO+CSNN算法在不同菌群规模下的渲染时间预估性能,差异化设置菌群规模,验证不同规模下BFO+CSNN算法对样本渲染时间的性能。

从图2得,在不同菌群规模下,采用BFO+CSNN算法获得的渲染时间差值呈现了较大波动。当菌群规模为500时,对于大部分样本,其渲染时间差值最优,预测误差基本维持在10 s范围之内,菌群规模为1 000次之,菌群规模为100时,预测和实际的渲染时间误差最大。其中当菌群规模为100时,渲染时间的预测值和实际值相差最大,最大值达到了58 s。对于图中某些样本点误差增大明显的情况,这可能是因为样本特征本身复杂,需要消耗大量渲染时间,造成的累积误差大,另一方面也可能是BFO+CSNN算法本身对某些特征样本的渲染时间预测适应度差。虽然在菌群规模为1 000时,有些样本点的渲染时间误差小于菌群规模为500的情况,但是其占总样本数量非常少,因此本文在后续的仿真测试中选择的菌群规模均为500。

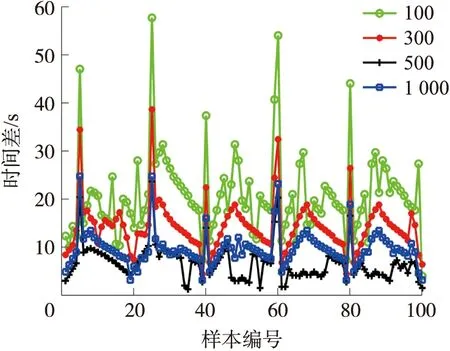
图2 不同菌群规模下的BFO+CSNN渲染时间差

对于100个样本,采用BFO+CSNN算法进行渲染时间估计,统计100个样本的平均MAE和MAPE值,具体如表2。

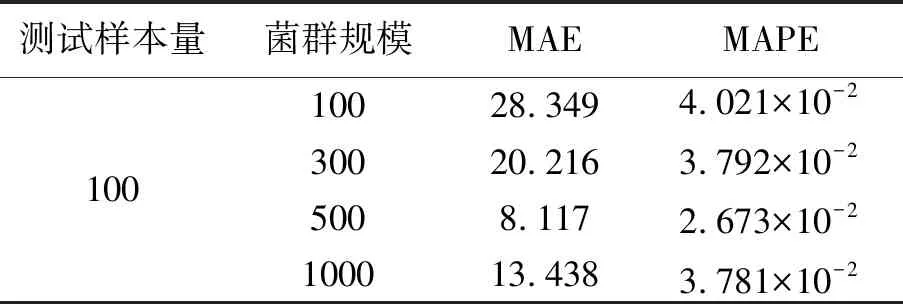
表2 不同菌群规模的MAE和MAPE性能

从表2知,随着菌群规模的增大,BFO+CSNN算法所得到的渲染时间预估准确率先升后降,在菌群规模为100时,MAE和MAPE均最大,这表明渲染时间预估准确率最低,而当菌群规模升至300和500时,MAE和MAPE下降明显,这表明预估准确率提升明显,在菌群规模为500时,获得了最优MAE和MAPE值,分别是8.117和2.673×10-2;当菌群规模从500增至1 000时,预估准确率却出现了下降,这表明菌群规模并不是越大越好。菌群规模过小,在搜索CSNN参数最优值的过程中,不易找到全局最优值,而当菌群规模过大,增加了驱化求解次数,同时繁衍和迁徙的个体过多,增加了算法复杂度。综合而言,对于表1数据集,菌群规模为500时,BFO+CSNN算法的渲染时间估计适应度最高。在实际渲染时间预估应用中,应结合样本特点,采用人工经验选择菌群规模,以增强 BFO+CSNN算法的渲染时间估计适用性。

3.2 BFO对CSNN渲染时间预估的性能优化

为了验证BFO对CSNN渲染时间预估的优化性能,分别采用CSNN算法和BFO+CSNN算法进行渲染时间预估仿真,菌群规模为500。

由图3和图4可得,对于表1测试样本的渲染时间,BFO+CSNN算法的渲染时间预测值和实际值拟合程度明显高于CSNN算法,CSNN算法的渲染时间预测值普遍低于渲染时间实际值。这表明渲染时间准确率对于CSNN模型的参数依赖程度高,采用BFO算法对CSNN核心参数进行优化之后,CSNN的渲染时间预估结果明显优于随机设定参数的渲染时间预估结果。

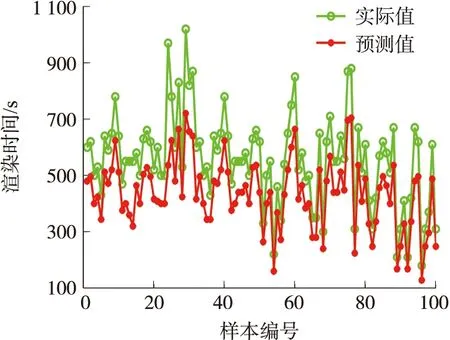
图3 基于CSNN算法的渲染时间

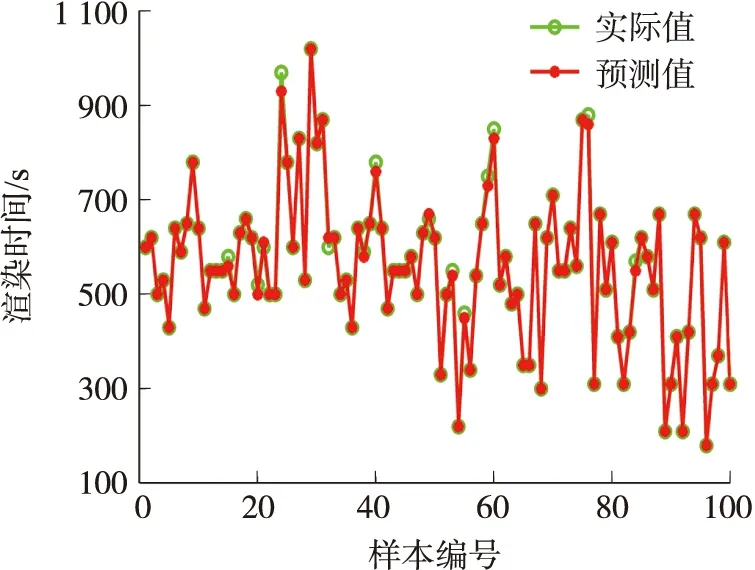
图4 基于BFO+CSNN算法的渲染时间

继续对CSNN和BFO+CSNN两种算法的RMSE和MAE性能进行仿真,如表3所示。分别采用两种算法执行了10次渲染时间估计运算,并对多次运行结果的评估指标取平均值。

表3 CSNN和BFO+CSNN的渲染时间预测性能

从表3得,CSNN和BFO+CSNN算法对于表1中样本集的渲染时间估计误差和鲁棒性差异较大,经过BFO改进的CSNN获得了更高的性能。在MAE性能方面,CSNN均值为42.342,而BFO+CSNN均值为8.117,经过BFO优化后,MAE性能提升了80.83%,而MAPE性能提升了79.72%。从2种算法的RMSE均值可知,BFO+SCCN的渲染时间估计模型鲁棒性更高。

3.3 不同算法的渲染时间预估性能

为了进一步验证BFO+CSNN算法和不同神经网络算法的渲染时间预估性能,分别采用BFO+神经网络(BFO+NN)、BFO+卷积神经网络(BFO+CNN)、BFO+循环神经网络(BFO+RNN)算法和BFO+CSNN算法进行实例仿真,菌群算法规模为500,验证其渲染时间预估性能。

从图5可以看出,对于表1中的数据样本,BFO+CSNN算法的渲染时间预测值和实际值拟合程度最好,BFO+RNN算法次之,BFO+NN算法最差。这表明本文算法在3D图像样本渲染时间预估中的领先优势明显。从侧面反映在解决多维属性特征和多变量的预测分析的问题上,采用Spiking神经网络优于传统神经网络算法。这得益于Spiking神经网络特有的脉冲编码模型结构。

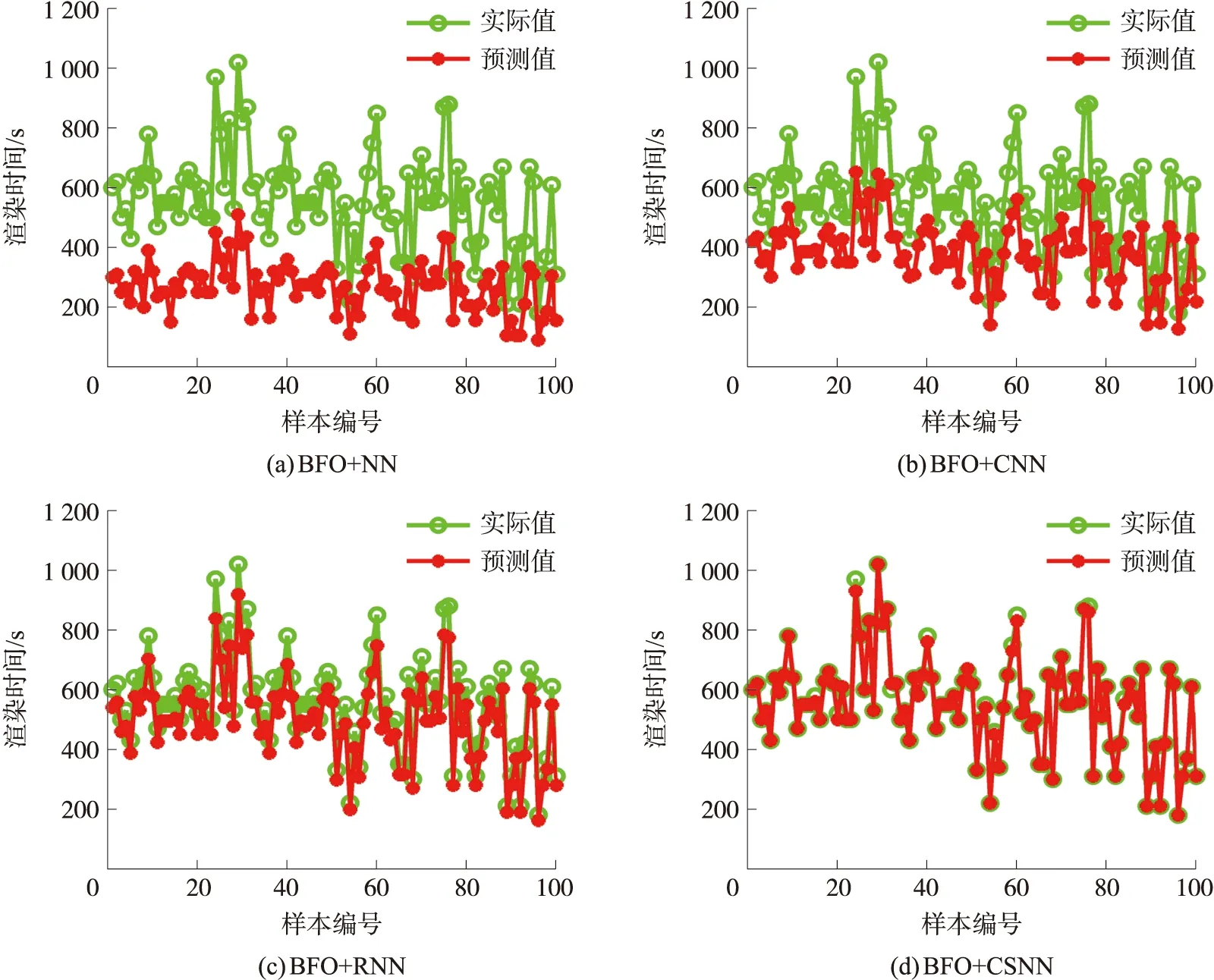
图5 4种算法的渲染时间对比

4 结束语

采用BFO+CSNN算法用于渲染时间估计,有效解决了大规模3D图像样本的渲染时间预测,为3D图像渲染的调度策略提供了数据支持。而采用BFO算法能够对CSNN的关键参数进行有效优化,从而提高了CSNN算法的预测性能。通过和常用神经网络算法对比,BFO+CSNN算法具备明显预测优势,展现了更高的渲染时间预估准确率度和鲁棒性。后续研究将进一步差异化设置BFO算法的主要参数,以提高BFO+CSNN算法的渲染时间预估效率,从而增强大规模3D图像样本渲染时间预测的适应度。