在复习中实现学生思维的进阶

江苏省南京市文靖东路小学 戴庆花

“整理与复习”是苏教版数学每个单元后知识的总结与归纳，意在引导学生自主整理本单元的学习内容，对本单元的知识点进行梳理与回顾。复习课既不能像新授课那样让学生感受到知识碰撞的激情，也不能像练习课那样让学生感到思维的不断延伸与拓展，但复习可以促使学生回忆，进而加深对知识的记忆与理解。

因此，新课授完后及时组织复习，帮助学生建立良好的认知结构，促进学生记忆与思维的发展是非常有必要的。怎样把学生已有的知识经验进行知识重组？怎样提升学生的数学思维？怎样通过自主构建让学生再次去学习数学，获取知识，实现对数学知识的再发现与再创造？怎样让学生牢固掌握和灵活运用所学知识解决问题，为后续学习打下坚实的基础？这些都是值得教师深入思考的问题。下面，笔者以苏教版数学六年级上册“长方体和正方体的整理与复习”一课为例，谈一谈自己的认识。

一、了于心——重梳理

复习时，笔者先让学生自主回忆所学的主要内容，并让学生在小组内讨论、交流，将旧知不断提取、再现；再根据学生的回忆，进行从点到线、由线及面的小结，做到由一个知识点穿成一条知识线，连成一个知识面。“梳”的过程就是学生对已有知识进行梳理的过程，是同伴之间沟通的过程，是将所学知识融会贯通的过程。笔者通过“梳”，让学生对所学知识了然于心。

“认识长方体与正方体”单元的知识点主要有四大块，随着时间的推移，学生往往是学了后面的知识，忘了前面的知识，因此教师要引导学生对旧知进行回顾、提取与再现。在复习时，教师可通过创设情境激发学生自主整理的欲望，让学生以积极的心态主动参与其中，多角度、多方向整理本单元的知识点，让学生成为真正意义上的学习“小主人”。

师：关于长方体和正方体，你们知道哪些知识？请大家回顾与整理一下。

生1：我知道长方体和正方体的特征。

生2：我认识了它们的展开图。

生3：我知道什么是长方体和正方体的表面积和怎样求它们的表面积。

生4：我还知道什么叫物体的体积和容积、怎样求他们的体积和容积。

生5：我也知道测量体积或容积，要用体积或容积单位。

生6：我还知道长方体、正方体的立体图和三视图。

……

笔者根据学生的回答，及时展示学生的作品（作品略）。同时，让学生相互间进行交流、补充。

复习的过程是学生交流信息的过程，在这个过程中，学生是主体，教师是引导者，教师要把复习的主动权交给学生，让学生在宽松的学习氛围中进入复习状态，引导学生自主整理知识。学生根据已有知识自主整理，用自己的方式去理解、去梳理、去重建数学知识。这样不仅有利于学生学习技能的提高，还有助于学生在交流中认识自己、发现自己，不断地完善自己。

二、简于形——建体系

笔者根据学生的整理与交流，汇总重点知识，进行板书，形成本单元的思维导图（图略）。

在复习过程中，教师引导学生对数学知识加以系统整理，依据基础知识的相互联系及相互转化的关系，分类梳理、分块整理，使零散的、碎片化的知识点变为系统的、条理化的知识网，最终使学生将所学的分散的知识系统化。对学生而言，复习不再是知识的终极，而是又一个新的起点，是探索、实践、再实践的循环过程，是逐步实现知识网络化的渐进过程。

三、精于练——提能力

复习时要展示学生的思维过程。教师可以通过说理训练帮助学生拓展思维，形成认知结构。而要把知识转化成认知结构，必然要以创造性的综合训练为手段，以提高学生综合能力为目标。因此在复习时，教师要选择富有典型性、针对性、系统性和启发性的问题，引导学生进行练习，使学生通过练习不断受到启发，在练习中进一步形成知识结构，不断提升综合能力。

（一）突出沟通与比较，加强题组练习

在复习时，笔者出示了这样一组对比练习：

1.一个长方体纸盒，长4分米，宽3分米，高10分米。做这样一个纸盒至少需要多少平方分米的硬纸板？

2.一个长方体纸盒，长4分米，宽3分米，高10厘米。做这样一个纸盒至少需要多少平方分米的硬纸板？

3.一个长方体通风管，高10分米，通风口长4分米，宽3分米，做这样一个通风管至少需要多少平方分米的铁皮？

笔者设计练习时从学生的认知规律出发，既让学生的练习有层次，又注重变式与发展，将一些易混淆的习题进行对比辨析，揭示解题规律，帮助学生排除知识间的干扰，培养学生思维的准确性。

（二）抓住知识间的联系，设计一题多解练习

笔者出示图形（见图1），要求学生求图形的表面积。

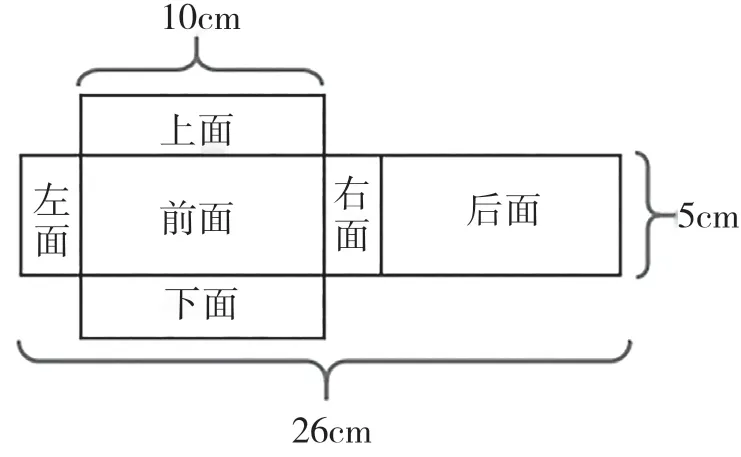
图1

学生在求解过程中，形成了三种解题方法。

方法一：先求出宽，再求出表面积。

表面积：（26-10×2）÷2=3（cm），

（10×5+3×5+10×3）×2

=（50+15+30）×2

=95×2

=190（cm2）

方法二：先求出宽，然后求出前后左右形成的长方形的面积，再求出表面积。

（26-10×2）÷2=3（cm）

26×5+10×3×2=190（cm2）

方法三：先求出宽，然后求出上面、下面、前面的面积+后面、左面、右面的面积。

（26-10×2）÷2=3（cm）

10×11+16×5=190（cm2）

复习课的练习是帮助学生全面掌握知识、形成技能，提升思维的有效途径。教师要利用知识之间的联系，引导学生将各类知识加以综合运用，注重同中求异、异中求同，培养学生的求异思维与发散思维。

（三）借力动手操作，设计数形结合的练习

笔者出示练习题。（见图2）

图2

学生根据三视图，求出一共有多少个正方形，然后求出不规则图形的表面积。

表面积：2×2=4（cm2）

（5+4+3）×2×4

=24×4

=96（cm2）

体积：2×2×2=8（cm3） 8×6=48（cm3）

在复习课中，教师要紧扣知识的混淆点、易错点，设计多样化的练习，帮助学生系统整理知识；设计对比性的练习，帮助学生沟通与辨析；设计综合发展的练习，提高学生的解题能力。教师还要通过设计不同层次的练习，让不同学生表现出不同的思维过程，真正使不同层次的学生得到不同的发展；让不同思维特点的学生有机会表达出自己的探索过程。同时，教师要根据学生学习上的差异性，让他们运用已有知识找出各种解法，体现出学生主观意义上的创造性。教师不仅应重视自己的“导”，更应重视学生的“学”，让学生主动参与、自主探索，使“学”的过程成为思维激活的过程，让学生真正成为学习的探索者、发现者。

四、延于外——再创造

数学知识来源于生活，教师要积极创造条件，为学生创设生动的生活问题，并鼓励学生善于发现生活中的问题，养成运用数学知识观察和分析生活现象的习惯，提升运用所学知识解决问题的能力。

弗赖登塔尔认为，数学实质上是人们常识的系统化。因此，学生可以在教师的引导下，通过自身的实际活动来获取数学知识，这个过程被称为“再创造”。在复习中，教师要留给学生思考的时间和空间，让学生感觉到复习不仅仅是旧知的再现，更是富有挑战性的学习，从而更加积极主动地投入知识的重新组建中，更好地发挥创造性，进而主动地认识与探索数学世界。

笔者在复习课中设计了这样一道练习题：设计师设计了三种糖果盒，但对于哪种糖果盒的性价比最高，厂长有些举棋不定，请同学们帮他选一个。看看你有什么好方法。

出示三种规格的盒子（略）。

生：要糖果盒装的糖最多。

师：有道理。你能求出糖果盒的容积吗？

生：要测量出每个盒子的长、宽、高。

（学生测量出：①号长25厘米、宽16厘米、高14厘米；②号长28厘米、宽20厘米、高10厘米；③号长35厘米、宽20厘米、高8厘米。学生计算后，发现体积一样）

师：体积一样，选哪个呢？（面露为难色）

生1：我认为③号样式比较美观。

生2：我认为①号携带方便。

生3：我认为还应该从材料方面去考虑，可以节约成本。哪个盒子的表面积小，就用料少。

……

“海阔凭鱼跃，天高任鸟飞。”教师要给学生一个自由翱翔的思维空间和自主表现的舞台，并能多角度、多方位、多层次启发学生解决问题的思维，拓宽学生的思维空间，从而有效培养学生思维的有序性、深刻性和周密性。

综上所述，数学复习的过程，实质上就是学生认知结构不断重组的过程，构建良好认知结构的过程。教师要在复习内容的安排上，让学生拾级而上，顺利攀登训练的最高峰。同时，教师要设计多样有趣的练习形式，让学生更乐于学习，能力训练范围更宽广，思维变得更灵活、更深刻。