集成正态云和动态扰动的哈里斯鹰优化算法
2023-05-23王俊杰李爱莲全凌翔崔桂梅
张 帅,王俊杰,李爱莲,全凌翔,崔桂梅
(内蒙古科技大学 信息工程学院,内蒙古 包头 014010)
1 引 言
元启发式算法是近年来兴起的一种智能优化技术,灵感源自生物行为、物理现象及数学概念等,用来解决实际工程中的复杂问题.常见的优化算法包括引力搜索算法(Gravitational Search Algorithm,GSA)[1],正弦余弦优化算法(Sine Cosine Algorithm,SCA)[2],灰狼优化算法(Grey Wolf Optimizer,GWO)[3],鲸鱼优化算法(Whale Optimization Algorithm,WOA)[4]等.哈里斯鹰算法(Harris Hawk Optimization,HHO)[5]是Heidari等人通过模拟哈里斯鹰捕食行为提出的一种新式优化算法,该算法由于结构简单,调节参数少和收敛精度高等特点,已被广泛应用于多个技术领域.文献[6]将HHO算法应用于卫星图像分割,实验结果表明,提出的融合变异机制的HHO阈值分割技术优于传统技术.文献[7]将HHO算法应用于到达时差定位问题,通过仿真对比其它算法得到更高的定位精度.
然而,与其它智能优化算法相同,HHO算法同样存在收敛速度慢,易陷入局部寻优等问题.针对这个问题,不少专家学者对HHO算法进行了改进.例如:文献[8]将信息交换改进机制和混沌扰动非线性逃逸因子引入基本HHO算法,增强了算法的收敛精度和鲁棒性.文献[9]提出了一种多子群个体交换的方法来改进HHO算法,有效提高了算法的寻优能力和收敛精度.文献[10]在基本HHO算法中引入柯西函数变异,用来提高种群多样性,同时用随机收缩指数函数修正猎物能量E.最后,引入自适应权重因子提高局部开发能力.文献[11]在基本HHO算法中引入了精英反向学习机制,用来提高种群多样性,同时利用黄金正弦算法改进哈里斯鹰捕食方式,增强了算法的局部开发能力.
针对基本HHO算法不足之处,本文提出集成正态云模型和动态扰动策略的改进哈里斯鹰算法(Improved Harris Hawks Optimization,IHHO).首先通过正态云模型和反向学习思想,在算法全局搜索阶段对哈里斯鹰位置进行更新,提高算法全局搜索能力.其次,在算法局部开发阶段加入动态扰动策略,以增强算法局部寻优能力.
2 哈里斯鹰优化算法
HHO是近年来新提出的一种元启发式智能算法,源自大自然中哈里斯鹰的捕食行为.哈里斯鹰首先栖息在猎物的潜在位置,然后通过猎物能量来采取不同策略进行捕食.HHO主要包括全局探索阶段、转换阶段和局部开发阶段.图1为HHO算法在不同阶段的示意图.
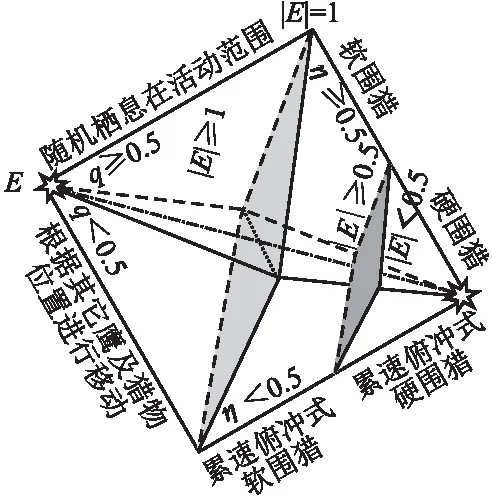
图1 HHO不同阶段示意图
2.1 全局探索阶段
在此阶段,哈里斯鹰随机分布在空间中,通过两种不同的策略去搜探空间中的猎物,且在迭代时通过q进行位置更新,公式如下所示:
(1)
(2)
其中:Xt+1和Xt分别表示哈里斯鹰在第t+1次和第t次迭代时的位置,Xrant和Xrabbit分别表示第t次迭代时哈里斯鹰的随机位置和猎物位置,Xm,t表示第t次迭代时哈里斯鹰的平均位置,r1,r2,r3,r4和q均是[0,1]中的随机数,ub和lb分别为维度空间的上下界.
2.2 转换阶段
哈里斯鹰算法通过猎物能量E来切换探索和开发,公式如下所示:
(3)
E0=2*rand-1
(4)
其中:T为最大迭代次数,E0为[-1,1]的随机数.
2.3 局部开发阶段
在此阶段,为了更好模拟哈里斯鹰实际捕食行为,算法根据哈里斯鹰的不同捕食方法提出了4种策略对开发阶段进行更新,并通过猎物能量和逃逸因子来选择具体策略.
2.3.1 软围猎
当|E|≥0.5且η≥0.5时,猎物能量E充足,能通过跳跃方式来躲避围猎,哈里斯鹰通过消耗E,最终成功捕获猎物,位置更新公式如下所示:
Xt+1=△Xi-E|JXrabbit,t-Xi|
(5)
△Xt=Xrabbit,t-Xt
(6)
J=2(1-r5)
(7)
其中:J为猎物跳跃强度,r5为[0,1]中的随机数.
2.3.2 硬围猎
当|E|<0.5且η≥0.5时,猎物因为能量E不足而被哈里斯鹰捕获,位置更新公式如下所示:
Xt+1=Xrabbit,t-E|△Xt|
(8)
2.3.3 累速俯冲式软围猎
当|E|≥0.5且η<0.5时,猎物能量E充足,有机会躲避围猎,首先哈里斯鹰对猎物进行俯冲式突袭,若突袭失败,则执行随机游走策略.
(9)
其中:D和S分别为问题维度和1×D维随机向量.LF定义如下所示:
(10)
其中:LF(x)为Levy飞行函数.
2.3.4 累速俯冲式硬围猎
当|E|<0.5且η<0.5时,猎物能量E不足,哈里斯鹰在突袭猎物之前会组织硬包围来进行捕食,若突袭失败,则执行随机游走策略.
(11)
3 改进哈里斯鹰优化算法
相对其它元启发算法,HHO算法也存在种群多样性下降、易陷入局部寻优等问题,本文从3方面对基本HHO算法进行改进.首先引入正态云模型来提高算法的种群多样性,其次为了提高全局搜索能力,对全局最差值进行反向学习,最后引入动态扰动策略,进而提高算法的局部开发能力.
3.1 正态云模型
云模型由期望Ex、熵En和超熵He3个参数进行描述,正态云模型中云滴的分布情况与数字参数的关系如图2所示,可以看出当En增大时,云滴分布范围随之变大,当He增大时,云滴的离散程度同步增大,侧面反映云滴分布的随机性和模糊性.正向正态云发生器是产生基本服从正态分布云滴的一种算法,通过设定的参数来产生云滴,直到生成期望的云滴数量.正态云滴生成过程可定义为如下所示[12]:
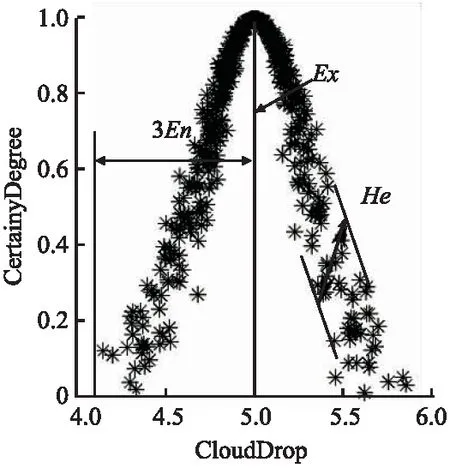
图2 云滴正态分布模型图
X[x1,x2,…,xNd]=Gnc(Ex,En,He,Nd)
(12)
其中:Nd为期望云滴个数.
本文引入正态云模型作为哈里斯鹰位置新的更新机制.通过正态云模型的期望值Ex对最优位置解进行开发,通过En调控其余位置解,利用He调整哈里斯鹰位置离散程度,公式如下所示[13]:
(13)
(14)
He=En×10-ξ
(15)
3.2 随机反向学习思想
反向学习思想自被提出以来,就成为优化算法常用的一种改进策略,主要是通过对算法可行解进行反向学习,通过评估原始解和反向解,选取更优解加入算法迭代.为此,本文引入随机反向学习思想对最差哈里斯鹰位置进行更新[14],公式如下所示:
Xworst,t+1=ub1+rand×(lb1-Xworst,t)
(16)
其中:Xworst表示最差哈里斯鹰位置,ub1和lb1分别为动态边界的上下界.
随着算法迭代,通过式(16)对位置最差值进行更新,得到反向随机解,从而提高哈里斯鹰种群多样性和寻得全局最优解几率.同时随机反向学习采用动态边界ub1和lb1,降低了传统的固定边界ub和lb易丢失搜索信息的问题,也降低了改进算法的计算复杂度.
3.3 动态扰动策略
当猎物能量|E|<0时,算法进入开发阶段,但无法保证此时种群都接近全局最优,可能会导致收敛太早以及陷入局部寻优.因此,本文受到文献[15]启发,在4种捕食策略中引入了一种动态扰动策略,在保证算法寻优精度的基础上能迅速跳出局部寻优.
(17)
Xψ,rabbit=ψ×Xrabbit
(18)
其中:ψ为扰动系数;Xψ,rabbit为加入扰动后的猎物位置.
3.4 改进算法的流程
改进哈里斯鹰算法(IHHO)的算法流程图如图3所示.
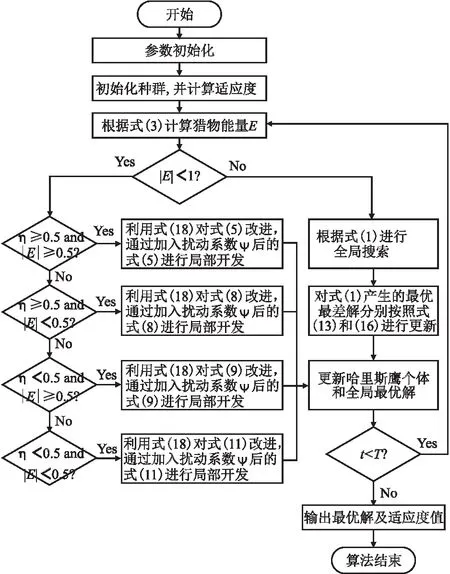
图3 IHHO流程图
4 仿真实验与结果分析
为了验证本文提出的IHHO改进策略有效性,将IHHO与GSA[1]、SCA[2]、GWO[3]、WOA[4]和HHO[5]在15个标准测试函数中通过均值(Avg)和标准差(Std)进行对比分析.本次仿真环境为:Windows10,Intel core i5-6300HQ,编程语言为MATLAB R2018a.算法主要参数设置如表1所示.为了仿真公平性,所有算法种群数设置为30,最大迭代数为500,各算法对每个测试函数均独立运行30次.

表1 算法参数设置
4.1 测试函数结果分析
在15个标准测试函数中,其中:F1~F6为单峰函数,主要用来检验算法的局部开发能力;F7~F12为多峰函数,用来测试算法的全局寻优能力;F13~F15为固定维度函数,侧重于测验算法全局搜索与局部开发的平衡能力.表2为测试函数基本信息[16].
表3为IHHO算法和对比算法在dim=30下的测试结果对比.从表3可以看出,IHHO在求解单峰函数F1~F6时,IHHO测试结果均优于对比算法,且在F1上取得了理论最优值,而且在F2~F4上均值和标准差相对于对比算法提高了上百个数量级.在求解多峰函数F7~F12时,IHHO和HHO在F9和F10均达到了最优值,且优于剩余4种对比算法,但IHHO在F11和F12上优于HHO和其它对比算法.在固定维度函数F13~F15求解时,IHHO在F13和F13上均优于对比算法,在F15上与5种对比算法寻优效果相当.经过上述测试结果分析,本文提出的改进算法具有更快的寻优速度和更优的收敛精度.
表4为IHHO算法和对比算法在下的测试结果.可以看出,IHHO在100维度下取得了与30维度下类似的结果.在单峰函数求解上,IHHO在F1上得到了理论最优值0,在F2~F4上虽未达到最优值0,寻优精度相对基本HHO分别提高了150个、250个和100个数量级.在F5和F6上寻优精度虽然与其它对比算法相似,但IHHO的均值和标准差均最小.在多峰函数求解上,IHHO和HHO在F7~F10上取得了相同的寻优结果,且在F8和F10上取得0解,除了WOA在F8上同样取得最优解外,IHHO在其它测试函数上均好于对比算法.
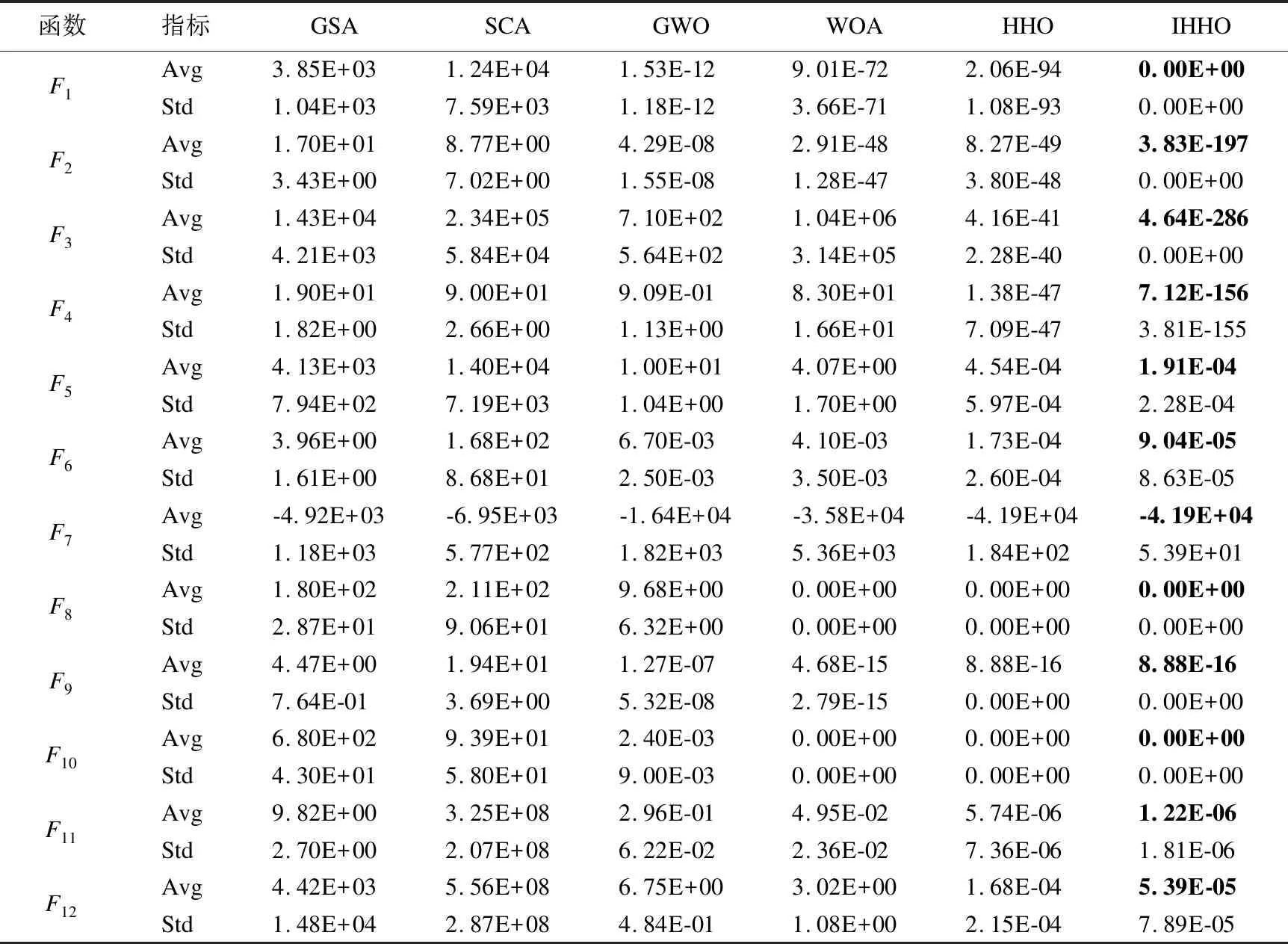
表4 不同算法测试函数结果对比(dim=100)
表5为IHHO算法和对比算法在dim=300下的测试结果.随着测试函数维度的增加,算法求解难度也大幅度提升,算法的收敛精度相对于低维度均不同程度下降.在F1~F4上,IHHO均大幅度优于5种对比算法,在F8和F10同WOA和HHO均取得了最优值,在其余测试函数上均好于对比算法,综上所述,IHHO在面对高维函数的优化问题上,改进策略仍具有可行性.
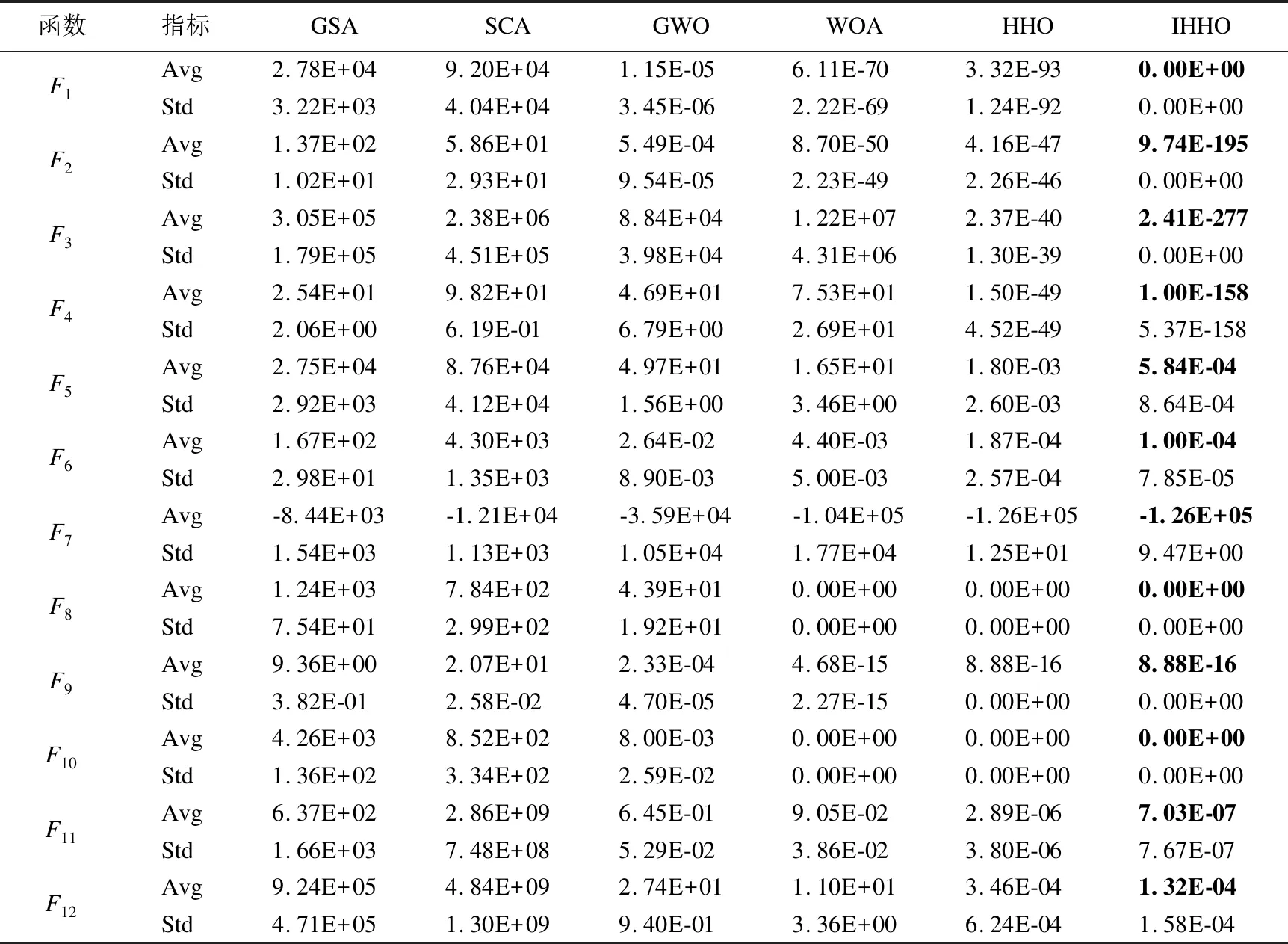
表5 不同算法测试函数结果对比(dim=300)
4.2 收敛曲线分析
为了更加直观反应算法的收敛性能,采用适应度值迭代曲线来进行算法性能比较.测试函数维度为30,迭代次数为500次,各智能优化算法参数设置同表1所示,各函数收敛曲线如图4所示,其中横坐标为算法迭代次数,纵坐标为函数适应度值.
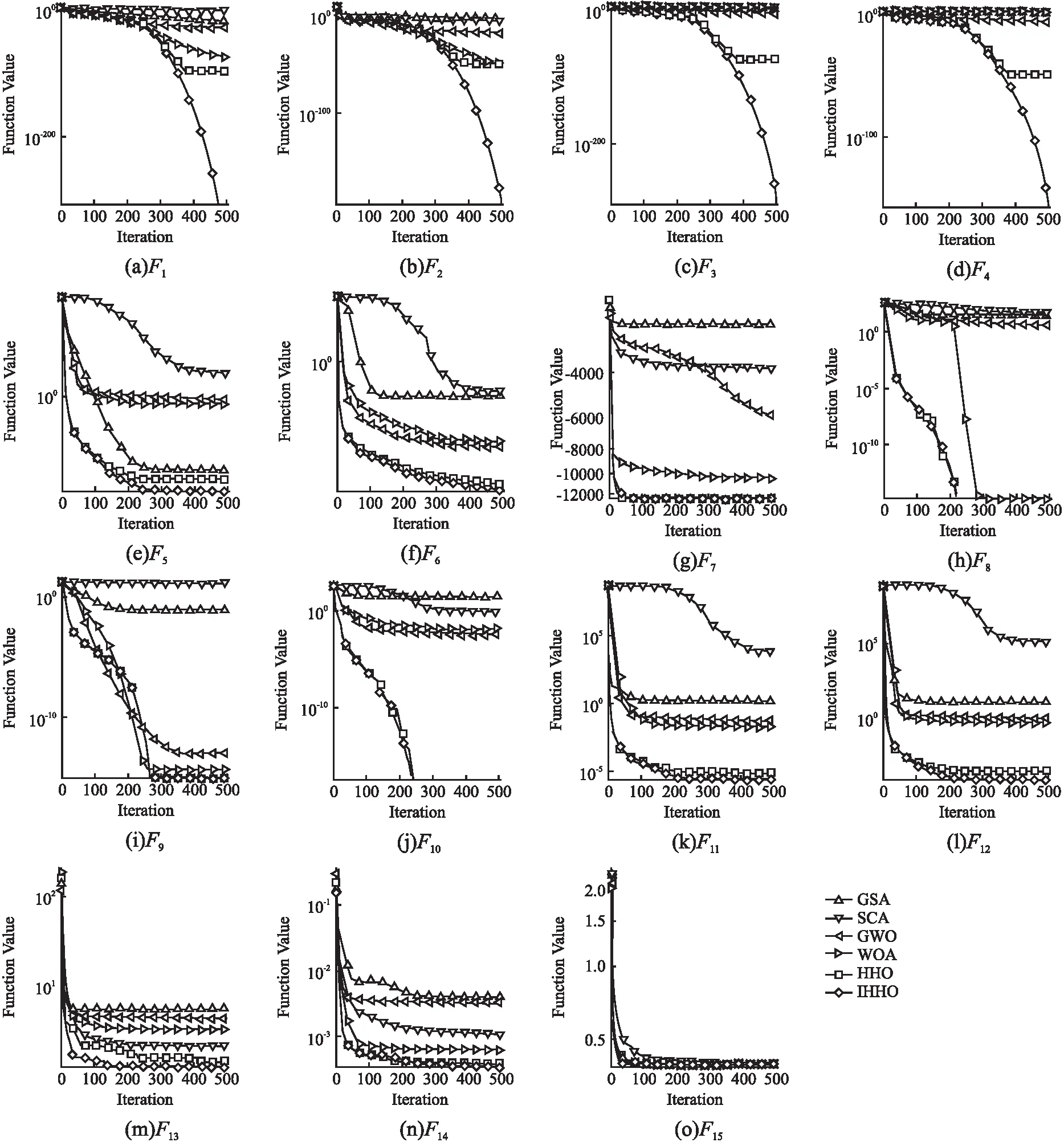
图4 测试函数收敛曲线图
从图4(a)~图4(d)看出IHHO在收敛精度上,相对对比算法显著提高.在图4(e)和图4(f)上略优于HHO算法,但对其余4种算法来说,寻优速度和收敛精度均有一定提高.验证加入动态扰动策略后,IHHO的局部开发能力有提升.在图4(h)和图4(j)上IHHO和HHO取得理论最优解,在多维函数求解上,由图4(m)和图4(n)看出,IHHO更具竞争力,说明IHHO在全局和开发上的平衡力领先其它算法.
4.3 算法统计检验
一般来说,单纯凭借均值和标准差来评判算法的性能往往不够精确,为了增加测试结果的说服力,引入Wilcoxon秩和检验[17]来评估IHHO在p=0.05显著性水平下与对比算法的显著性差异.当p<0.05时认为H0假设被拒绝,即算法之间存在显著性差异;当p>0.05时,认为同意H0假设,即算法之间差异性小,算法寻优性能相当.
表6为IHHO与GSA、SCA、GWO、WOA和HHO在dim=30和显著性水平p=0.05下的比较结果.其中:“NaN”表示无法进行显著性差异判断,“r”表示算法显著性差异判别,“+/=/-”表示IHHO算法和对比算法之间性能的“优于/相当/劣于”.由表6可得,绝大多数的p都小于0.05,可以证明,IHHO改进策略的有效性及与对比算法之间存在显著性差异的统计学意义.
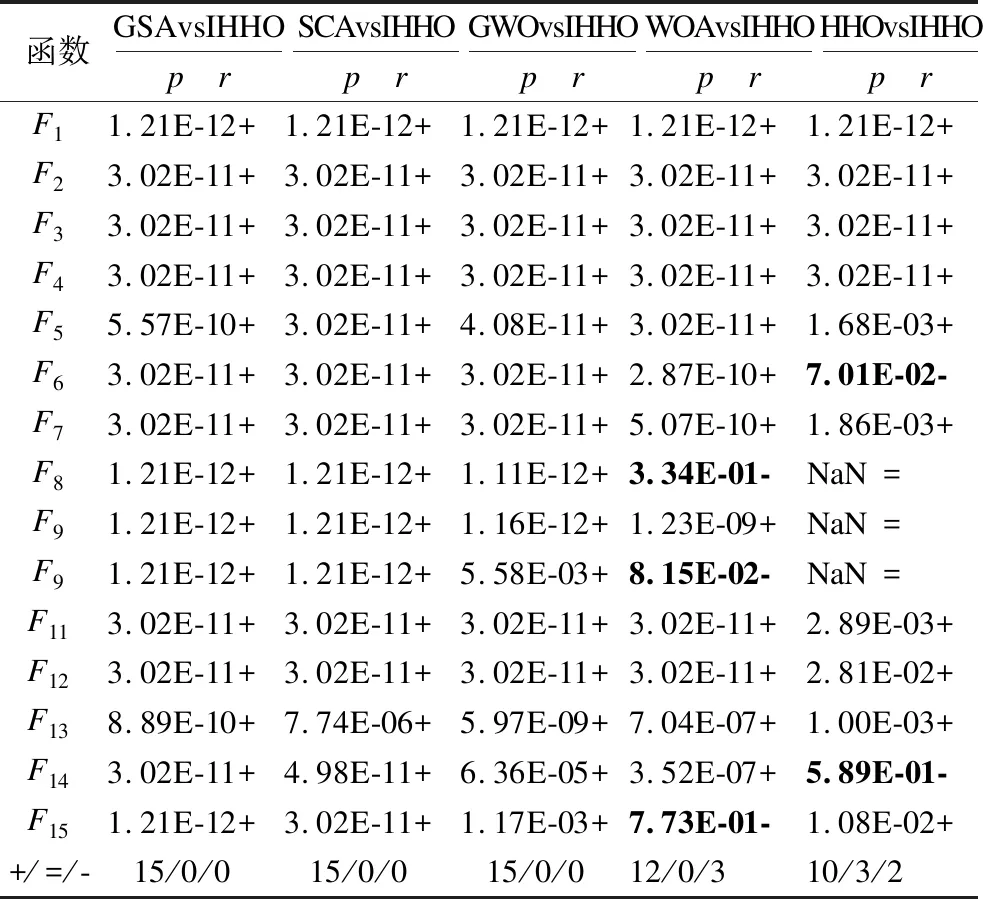
表6 Wilcoxon秩和检验结果
同时利用Friedman检验[18]通过比较秩来对算法进行比较,表7为算法Friedman排名,根据秩均值来看,在下的15个测试函数中,算法的平均排名为IHHO>HHO>WOA>GWO>GSA>SCA,表明了IHHO相对其它算法,性能方面更具有整体优越性.
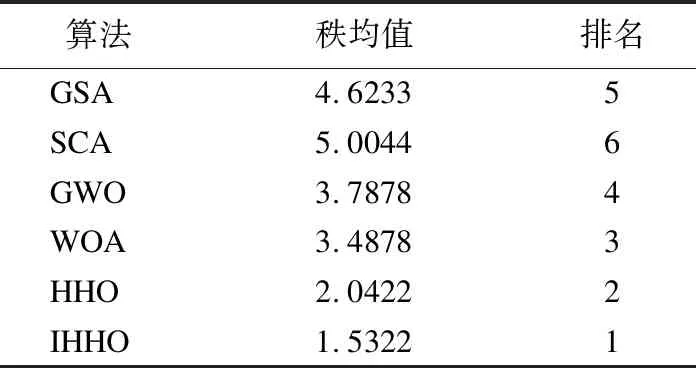
表7 算法Friedman排名
4.4 不同改进哈里斯鹰算法对比
为了进一步验证IHHO改进策略的有效性,将本文提出的IHHO与文献[19]中的hHHO-SCA,记作HHHO,文献[20]中的LHHO和文献[10]中的MHHO进行对比分析,为了仿真一致性,设置测试函数维度为30,种群数为30,最大迭代次数为500,选取各改进算法在每个测试函数上独立运行30次的平均值(Avg)和标准差(Std)进行分析.表8为不同改进策略哈里斯鹰算法对比,其中HHHO数据取自文献[19].通过表8可以看出,本文提出的IHHO仅在F5、F11和F12上略逊于MHHO,但基本处于一个数量级,寻优精度相差不大,其余测试函数上均好于对比的改进HHO算法,证明了本文提出的改进策略同其它改进策略相比,仍然具有优越性.
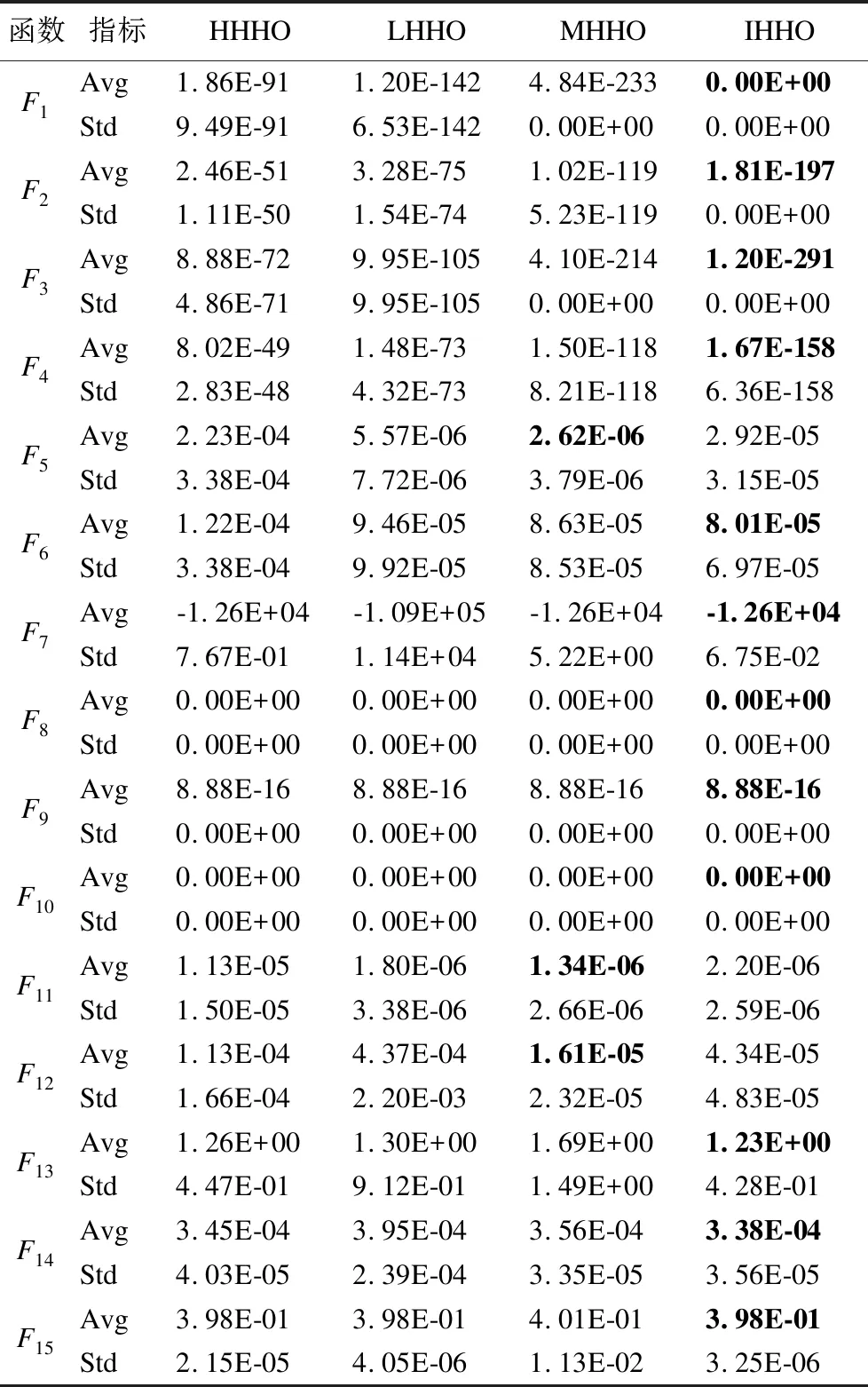
表8 不同改进HHO算法对比
4.5 实际工程应用
三杆桁架设计问题[5]是一种常用的用来检验改进算法性能的实际工程问题,设计目的是在满足要求的前提下最小化桁架的重量.结构示意图如图5所示,测试结果如表9所示,优化模型主要由一个适应度函数,3个不等式约束条件和2个决策优化变量组成,数学描述如下各式所示:
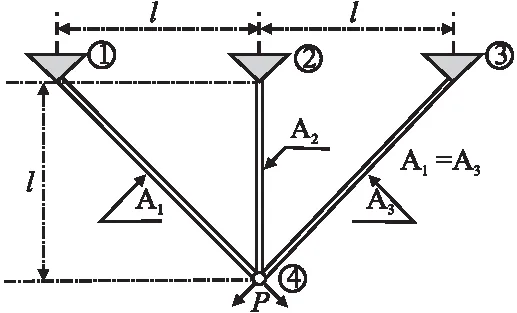
图5 三杆桁架设计结构图

表9 不同算法求解三杆桁架设计问题的对比结果
(19)
(20)
(21)
0≤xi≤1,i=1,2
(22)
l=100cm,P=2KN/cm2,σ=2KN/cm2
(23)
其中:l为挠度,P为屈曲,σ为应力.
根据表9结果,可以看出,IHHO与GSA、SCA、GWO、WOA和HHO等算法相比,在三杆桁架设计问题中寻优效果更好,进一步验证了IHHO在实际应用中的可行性.
5 结束语
本文针对基本哈里斯鹰算法寻优精度不高和收敛速度慢等问题,提出了一种集成多策略的改进哈里斯鹰算法.在全局搜索阶段,利用正态云模型和随机反向学习思想新全局哈里斯鹰位置,提高算法的全局搜索能力.在局部开发阶段,加入动态扰动策略,优化哈里斯鹰的捕食策略,从而提高算法的局部开发能力.通过15个测试函数进行仿真实验,并引入Wilcoxon秩和检验、Friedman检验,可以得出IHHO相较于其它5种优化算法和3种改进哈里斯鹰算法来说,寻优性能更为出色,最后通过三杆桁架设计问题,进一步证明了改进算法在实际应用中的可行性.在后续研究中,计划将改进算法用于热轧带钢层流冷却过程中,用更加复杂的实际问题来验证算法性能.
