随机缺失下阈值和灵敏性的联合估计

程伟丽,吴莹,左卫兵

(1.华北水利水电大学 数学与统计学院,郑州 450046;2.云南大学 数学与统计学院,昆明 650500)

在诊断医学中,受试者测试特征曲线(简称为ROC曲线)是常用的衡量连续型诊断检验诊断能力的一个统计工具.随着阈值的变化,正确诊断有病体的概率—灵敏性(Se)和正确诊断无病体的概率—特异性(Sp)会向相反方向变化,以1-Sp为横坐标,以Se为纵坐标,将这些点连起来就构成了ROC曲线.有关ROC曲线可以参看文献[1].

通过一个连续性诊断检验值来诊断受试者是有病或者是无病,需要选择一个阈值,最优阈值τ的选择非常重要.设有病体生物指标X和无病体生物指标Y的分布函数分别是F(·)和G(·),不失一般性,假设生物指标值越大越易患病.给定阈值τ,则灵敏性和特异性可表示为θ(τ)=Pr(X>τ)=1-F(r)和η(τ)=Pr(Y≤τ)=G(τ).通常选择在高特异性下的阈值,一方面这会使得阈值随着特异性的变化而变化,另一方面高特异性下的灵敏性不一定很高.为选择一个最优的阈值,现有文献提出了以下几种方法.文献[2]提出基于最大化正确分类两总体概率之和的约当指标的基础上选择最优阈值,即τ=arg maxτ|{θ(τ)+η(τ)-1}|.文献[3]提出用ROC曲线中最接近最好点(0,1)的方法选择最优阈值,即

文献[4]提出最大化灵敏性和特异性乘积的方法来确定阈值τ=arg maxτ[θ(τ)η(τ)].文献[5]提出基于两个总体被正确分类概率的基础上选择阈值,即τ=argτ{θ(τ)=η(τ)}.上面所有方法选择的阈值有可能是相同的,但是在一般情况下不同的方法选择的阈值是不同的.由于对称点准则容易推广到广义对称点准则,即τ=argτ{θ(τ)=η(τ)},ρ是灵敏性和特异性的相对重视度,若ρ=1,广义对称点就是标准对称点,鉴于不需要优化和实际分析中需要同等重视两总体被正确诊断的概率,本文选择基于对称点准则来确定阈值.

现有文献中,阈值与相应的灵敏性和特异性的估计有参数、半参数和非参数的方法.非参数估计由于受假定错误的影响少而备受关注.文献[6]用经验似然结合光滑化估计方程的方法在给定特异性的条件下估计灵敏性.文献[7]采用刀切经验似然结合非光滑估计方程的方法去估计给定特异性下的灵敏性.文献[8]用经验似然结合非光滑估计方程的方法在阈值、灵敏性和特异性三者中给定任意一个参数去估计剩余的两个参数.文献[9]在对称点准则下使用经验似然结合非光滑估计方程的方法去选择最优阈值和相对应的灵敏性.因此,本文也选择用两样本经验似然结合非光滑估计方程的非参方法.

在实际应用中,受试者有可能会由于各种各样的原因导致生物指标值的缺失,比如:研究中的退出,各种不可控因素引起的信息缺失,参看文献[10].因此近年来,在诊断检验值缺失的情形下,ROC曲线的统计分析受到了不少的关注.文献[11-12]研究了在完全随机缺失数据下通过随机热平台插补方法得到ROC曲线的估计和区间估计.文献[13]研究了随机缺失下经验似然结合光滑化估计方程的方法得到高特异性下灵敏性的估计和区间估计.但光滑估计方程中窗宽的选择是一个不易解决的问题.因此,本文研究生物指标值随机缺失情形基于对称点原则下两样本经验似然结合非光滑估计方程的方法给出阈值和灵敏性的联合估计和置信域.

1 缺失数据下阈值和灵敏性的经验似然估计

1.1 符号

1.2 两样本经验似然估计

在不存在缺失生物指标的条件下,阈值、灵敏性和特异性的两样本经验似然估计如下:基于两样本估计方程g1i(θ,η,τ,Xi)和g2j(θ,η,τ,Yj),定义参数(θ,η,τ)的两样本经验似然比函数

其中g1i(θ,η,τ,Xi)=I(Xi≤τ)-(1-θ),i=1,2,…,m,g2j(θ,η,τ,Yj)=I(Yj≤τ)-η,j=1,2,…,n.在对称点θ=η的要求下,上面的两样本经验似然比函数只是关于参数((θ,τ),矩函数g1i(θ,η,τ,Xi)和g2j(θ,η,τ,Yj)分别调整为g1i(θ,τ,Xi)=I(Xi≤τ)-(1-θ),i=1,2,…,m和g2j(θ,τ,Yj)=I(Yj≤τ)-θ,j=1,2,…,n.再如上定义两样本经验似然比函数是

上面的对数经验似然比在真值点的渐近分布是自由度为2的标准卡方分布.这里令真值点θ0,τ0分别表示θ,τ的真值,且满足E{[g1i(θ0,τ0,Xi),g2j(θ,τ,Yj)]T}=0的唯一解.

1.3 带有缺失数据的两样本经验似然估计

在实际应用中,π1(Zxi)和π2(Zyj)通常是不知道的.为此,考虑倾向得分函数π1(Zxi)和π2(Zyj)是下面的logistic回归模型:

(1)

(2)

因此,参数(θ,τ)的对数经验似然比函数是

(3)

2 渐近理论

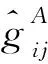
为证明结论,需要如下条件.

(C1)当min(m,n)→∞,有m/N→γ1,n/N→γ2,其中0<γ1,γ2<1.

(C3)倾向得分函数π1(Zx)和π2(Zy)满足miniπ1(Zxi)≥c1,对某个正数c1>0,minjπ2(Zyj)≥c2对某个正数c2>0.密度函数pzx(Zx)在Zx的支撑集上有界,关于Zx至少二阶连续可导;pzy(Zy)在Zy的支撑集上有界,关于Zy至少二阶连续可导.

(C4)存在参数β0=(θ0,τ0)∈B是矩函数φ(β)=0的唯一解.参数空B是R2紧子集,且E[supβ∈B|g(β)|]<∞和E[supβ∈B|g(β)gT(β)|]每个分量都有界.

(C7)对于所有的β∈B和所有的小正数=o(1),存在一个正数C和s∈(0,1],使得2s和2s成立.

(C8)当κ→∞时,矩函数的插补部分的条件期望mg1(β,Zx)满足条件:(i)函数族{mg1(β,Zx),(β)∈B}是Glivenko-Cantelli;(ii)对所有的Zx∈Z存在某个1>0满足在小邻域N关于参数β有连续的偏导数∂βmg1(β,Zx)=∂mg1(β,Zx)/∂β;E{supβ∈N1|∂βmg1(β,Zx)}的每个分量都有界;(iii)存在s1∈(0,1]和某个满足E[b(Zx)]<∞的可测函数b(Zx),对满足1的光滑函数有当κ→∞时,另一个矩函数的插补部分的条件期望mg2(β,Zy)有类似上面的要求条件.

条件(C1)是两样本的样本量平衡的条件,条件(C2)和(C3)是缺失数据中常要求满足的条件,条件(C4)～(C7)是非光滑矩函数需要满足的条件,条件(C8)是非光滑矩函数的插补部分需要满足的条件.

定理1假设上面的条件(C1)～(C8)成立,当min(m,n)→∞和κ→∞,则有

(4)

定理2假设上面的条件(C1)～(C8)成立,当min(m,n)→∞和κ→∞,则有

(5)

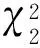
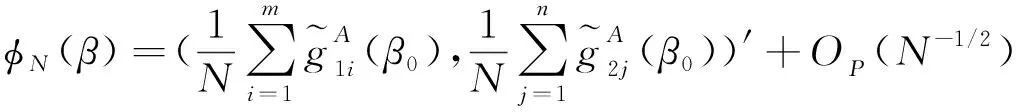
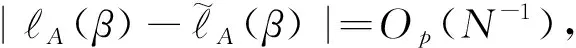
3 数值模拟

在这一节,实施两个模拟研究来调查提出方法的有限样本表现.为了便于比较,考虑以下几个估计:(1)GS估计,基于完整的数据集而不考虑缺失值计算的估计;(2)CC估计,只用完全观测数据的估计;(3)IPW估计,基于logistic倾向得分函数的逆概率加权方法的估计;(4)AIPW估计,基于logistic倾向得分函数的逆概率加权和多重插补方法得到的估计.

(a)logit{π1(Zxi)}=1,logit{π2(Zyj)}=1;

(b)logit{π1(Zxi)}=1+0.4Zxi,logit{π2(Zyj)}=1+0.4Zyj,其中logit(x)=ln{x/(1-x)};

(c)π1(Zxi)=Φ(0.6+0.4Zxi),π2(Zyj)=Φ(0.6+0.4Zyj),其中Φ(·)是标准正态分布的累积分布函数.

这里(a)是本文1.3小节定义缺失数据机制(1)的特殊情况,即α1,1=0和α2,1=0,这对应于完全随机缺失情况;(b)满足缺失数据机制(1)给定的随机缺失数据机制下的参数模型假设;(c)是随机缺失机制,但是不满足缺失数据机制(1)的参数模型假设,这主要是对错误设定倾向得分模型的稳健分析.按上面情形产生的平均缺失率大约在30%左右.

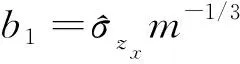
表1 样本量m=n=300 3种缺失设置下灵敏性和阈值的估计

表2 样本量m=240,n=360 3种缺失设置下灵敏性和阈值的估计

从表1可以看出,误差项若是正态分布,在所设置的3种缺失环境下,即便是在倾向得分函数的模型假定错误的情形下,增广逆概率加权估计的所有结果都接近于没有缺失数据下基准的GS的结果;在完全随机缺失(a)下,只用观测到数据的CC估计在标准差上比GS估计的标准差大,不过在偏差和覆盖率上也接近于GS的结果,但是非随机缺失(b)和(c)下,不但标准差增大,偏差也变大,覆盖率要远小于名义水平95%;与GS估计相比,逆概率加权估计的标准差虽然增大,但是偏差变化不大,覆盖率却远大于名义水平95%,这很可能是由于权重估计的不稳定造成的.若误差项是非正态分布,表2有相似的模拟结果表现.将误差项是正态分布和非正态分布情形3种缺失机制下阈值和灵敏性95%的非参置信域显示(图1),其中上面3个图是正态分布误差项下3种缺失机制(从左到右依次是a,b和c)的联合置信域,下面3个图是非正态分布误差项下3种缺失机制(从左到右依次是a,b和c)的联合置信域,点图是CC,实线是本文提出的方法.从图1中可以看出这两种估计是有差别的.