基于MVMD-CapSA-DBN的工业多元负荷分类研究

周孟然,张易平,汪胜和,马金辉,高博,胡锋,朱梓伟,汪锟,刘宇

(1.安徽理工大学 电气与信息工程学院,安徽 淮南 232001;2.国网安徽省电力有限公司,合肥 230001)

电力负荷的正常稳定运行以及实时监测对工厂稳定运行意义重大.为了保证电力系统的健康、经济、高效、可靠的运行,需要深入分析各类负荷特点,在此基础上进行需求侧管理,规划分时电价、移峰填谷等负荷管理工作,优化电网结构,提升电能利用效率,改善用户用电习惯[1].

目前针对电力负荷预测分类精度提升的研究主要从两方面考虑:1)数据信息提取方面,从时频域分解数据信号,收集数据有效信息,挖掘其隐含信息、信号重构减小噪声干扰;2)对负荷预测及分类方法研究,包括机器学习、深度学习等方法进行负荷预测、分类研究,改进聚类算法、神经网络等方法.经验模态分解(Empirical Mode Decomposition,EMD)作为自适应分解方法,在信号分解中应用十分广泛,徐岩等人[2]利用EMD,分解时域信号并重构,有效消除较多噪声信息,接着提取信号特征进行分类,分类精度得到提高;研究者为解决冲击信号损失得问题,采用EMD结合稀疏分解特征提取方式,提高了分类准确度[3].由于变分模态分解(Variational Mode Decomposition,VMD)[4]能够很好克服模态混叠、端点效应等缺点,所以一经提出,就被应用到信号分解方面,其在电力负荷分解方面表现也很好.商立群等[5]等针对光伏发电功率随机性和波动性较强的问题,为了提高预测精度,利用VMD对光伏发电功率序列进行平稳化处理,实验结果验证了其有效性和优越性;马宗彪等[6]采用VMD对数据模态分解重构,改善了FCM聚类精度就收敛速度慢的问题,实现了电力负荷的模糊分类.但采用VMD对信号分解,其分解量根据经验人为确定,具有不确定性,可靠性低的缺点,因此本文提出停止准则对其改进,增加分解分量置信度.

近几年采用深度学习预测分类[7-9]十分热门.其中深度置信网络[10](Deep Belief Nets,DBN)作为分类器,用于图像处理,手写字识别等,其在信号分类方面也有广泛应用.张建宇等[11]提出迁移诊断模型,构建特征识别参数,引入最大相关峭度反卷积法方法,采用DBN对所研究的3类滚动轴承分类,准确率达到95%.神经网络的参数设置对结果影响也很大.为对神经网络的参数合理设置,引入优化算法对使用的神经网络优化,程换新等人[12]利用循环神经网络对未来短期负荷预测,针对循环神经网络易陷入局部最优和全局搜索能力弱的缺点,利用改进后的粒子群算法优化循环神经网络的结点权值参数,有效提高预测准确度.

然而,关于电力负荷优化、科学管理方面的研究仍缺少对具体负荷清晰分类的讨论,难以精准调控实时负荷.针对以上问题,提出MVMD-CapSA-DBN模型对工业电力负荷分类.首先采用停止准则改进传统VMD[13-15],有效确定VMD分解量,对信号分解后提取特征.根据采集的工业电力负荷数据,针对已知负荷类别分类问题选用DBN分类[16].同时考虑DBN参数对结果影响较大的问题,提出利用卷尾猴搜索算法(Capuchin Search Algorithm,CapSA)[17]优化对DBN影响较大的参数.

1 理论介绍

1.1 MVMD-CapSA-DBN模型流程

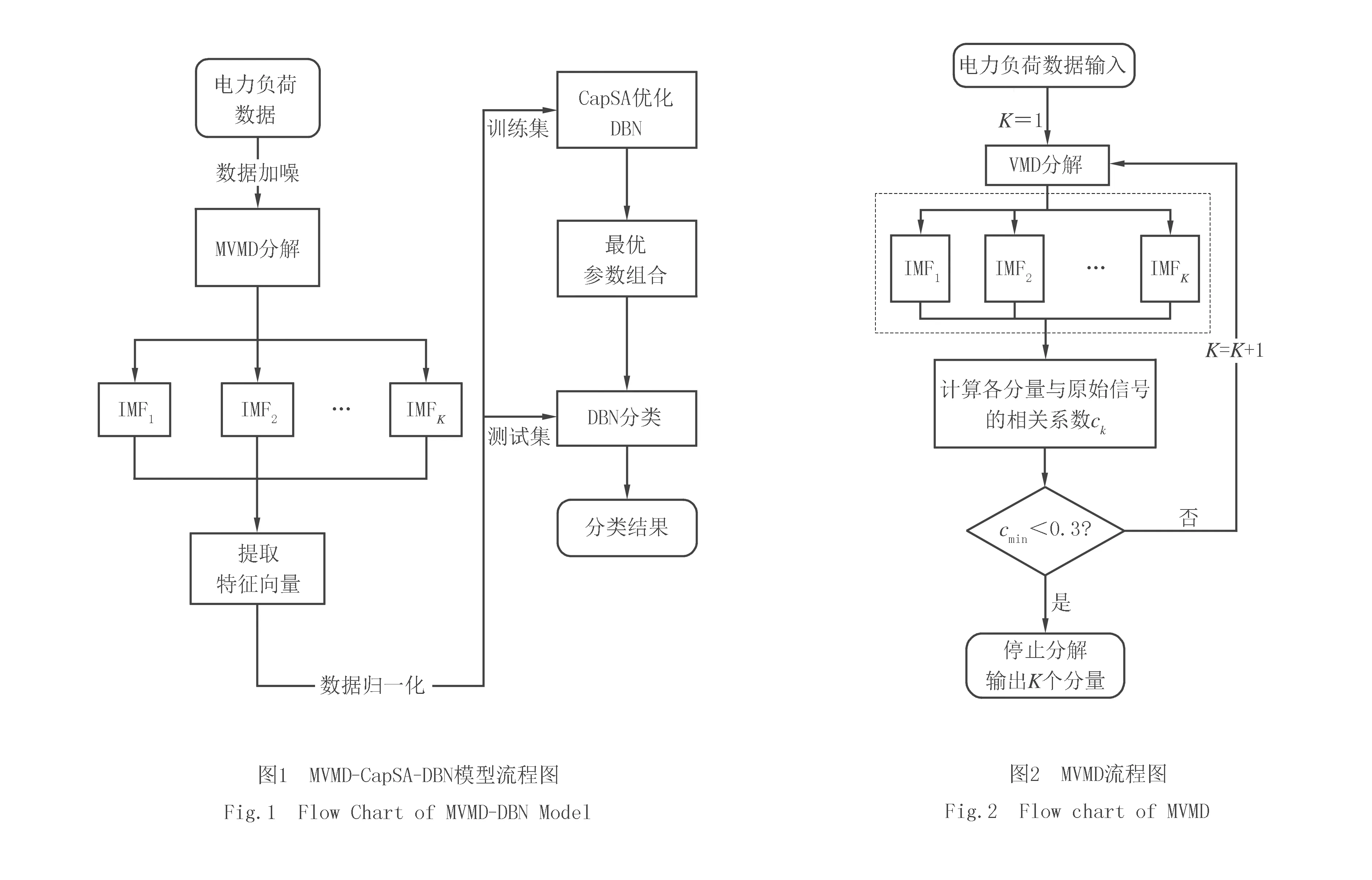
针对工业多元电力负荷信号易受干扰、特征不明显的特点,建立基于MVMD-CapSA-DBN分类信号模型.图1为MVMD-CapSA-DBN流程图.首先,使用MVMD对多元负荷的功率信号分解,得到较为平稳的多个模态分量;之后使用CapSA-DBN,得到最优参数的DBN神经网络,提取多元负荷经MVMD分解后的多个模态分量特征向量,输入优化后的DBN神经网络训练,通过soft-max进行分类.

该算法运用递归思想,改进了传统VMD算法模态分解数根据经验人为确定的不可靠性,分解分量数目的判定由各分量与原信号相关系数决定.确定分解模态数后,分解模态分量的能量值即为特征输出,大大降低了数据的特征维度,有利于提高神经网络的诊断速度.后采用卷尾猴搜索算法优化对DBN分类结果影响较大的参数,提高DBN分类准确度.

1.2 改进VMD介绍

1.2.1VMD原理

VMD对于复杂非平稳时间序列信号的适应度非常好[18],对电力负荷数据分解按下述公式.VMD分解的问题实质是构建和求解变分问题,求解约束变分问题最优解

(1)

其中,α为惩罚因子;λ为Lagrange乘子;f(t)为电力负荷功率信号;{uk}={u1,u2,…,uK}为分解K个模态分量;{ωk}={ω1,ω2,…,ωK}为中心频率;δ(t)为单位脉冲函数;*为卷积运算.

采用交替方向乘子算法(Alternate Direction Method of Multiplers,ADMM)更新迭代求解增广Lagrange式(1)的鞍点,在频域内迭代更新uk,ωk及λ.其迭代表达式如下

(2)

(3)

(4)

1.2.2停止准则

VMD分解的效果与分解模态数的取值具有十分相关性[19],较小的模态分解数会过滤一些需要的重要特征信息,影响后续分类准确率;而模态分解数过大则会有模态重复.传统VMD的模态分解数一般由经验法确定,可靠性差.由于K值选择对于特征提取意义重大,所以提出一种基于VMD分解的停止准则确定K值.

采用VMD分解方法分解出的K个信号分量IMF,其本质是原始信号的组成成分,也就是说分解出来的信号和原信号具有相关性.计算分解信号与原信号的相关系数ck,确定最小相关系数cmin,若小于阈值,停止分解.见图2.

1.3 DBN原理

DBN由Hinton 2006年提出,以数层受限玻尔兹曼机(Restricted Boltzman Machine,RBM)为基本构成模块,最后一层连接分类器构成的半监督神经网络.由于其深度学习能力较强,在信号分类方面表现很好,被广泛应用分类问题.

经典DBN由多层RBM堆叠,最后一层连接BP网络构成,其经典结构如图3.DBN网络的训练过程是由上到下一层一层进行的,首先输入提取的电力负荷特征数据进行无监督预训练,第一层RBM充分训练后再训练下一层;无监督训练后利用BP网络进行有监督训练,将最后一层RBM的输出作为输入给连接的BP网络进行有监督反向微调训练;完成训练.这种训练方式有效避免陷入局部最大值,学习信号特征.DBN的本质就是特征学习的过程.

1.4 CapSA原理

CapSA是于2021年提出的一种新型智能优化算法.该算法模拟猴子的动态行为.通过对卷尾猴在森林中游荡觅食时的行为进行建模,设计了算法的基本优化特性.具有寻优能力强,收敛速度快等特点.种群包括两种卷尾猴类型:领导者和追随者.追随者可能伴随领导者觅食,并追求类似的运动行为.其算法原理如下.

1)初始化种群

xi=uj+r×(uj-lj),

(5)

式中,上标i指第i个个体,下标j指第j维,x为个体的位置,u为上边界,l为下边界,r为[0,1]之间随机数.

2)卷尾猴寿命指数

(6)

式中,k、K为当前和最大迭代次数,β0=1,β1=11,β2=1.在全局和局部搜索过程中实现探索和开采之间的平衡.

第i只卷尾猴第j维速度

(7)

其中,x表示个体当前位置;xbest表示个体最佳位置;F表示食物位置;α1=1,α2=1;r1,r2均为[0,1]之间随机数;ρ=0.7.

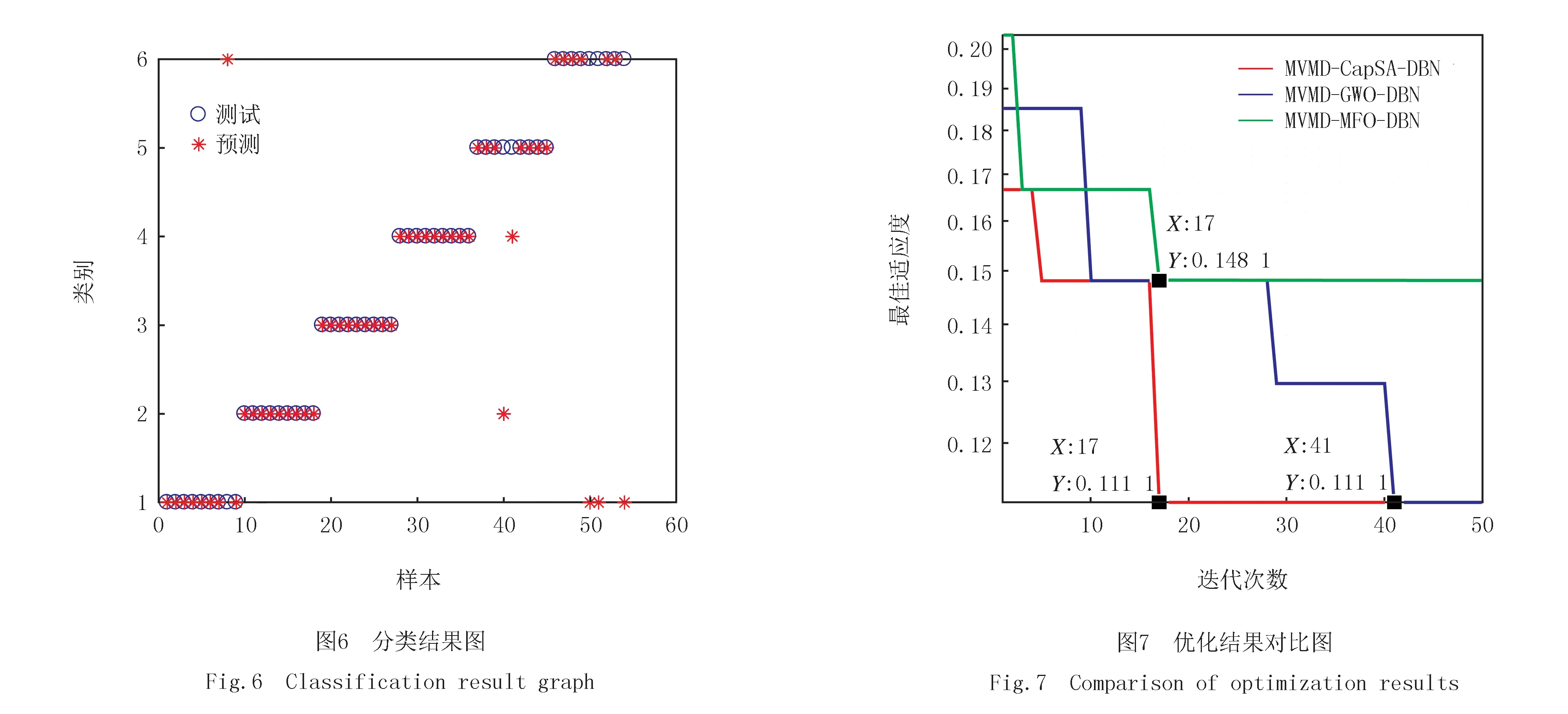
3)领导者α(i

(8)

式中,ε为[0,1]随机数;卷尾猴在地面运动弹性概率Pef=9;平衡系数Pbf=0.7;重力加速度g取9.81 m/s2;跳跃角度θ=2/3r.

4)追随者(n/2≤i≤n)位置

(9)

卷尾猴位置更新的过程即为优化过程,它们按照上述运动方式寻找食物,一段寻优时间过后,运动到食物周围,最佳寻优位置即食物所在位置.

1.5 CapSA优化DBN

DBN神经网络中各参数、隐含层数及隐含层神经元个数对结果均有影响[20-22],经实验显示,DBN具有两层隐含层其深度学习效果已经很好,所以模型确定隐含层为两层.动量m,学习因子α,隐含层RBM1和RBM2的神经元个数对结果影响较大,所以对DBN网络这4个参数进行寻优.将DBN网络结果误差作为目标函数.CapSA-DBN流程如下:

1)设置CapSA参数,算法初始化.设置卷尾猴数量,寻优范围,变量个数和最大迭代次数.

2)设置目标函数.将DBN网络训练误差作为寻优条件.

3)输入训练数据.将经MVMD获得的特征向量矩阵归一化后,取70%作为训练数据.

4)根据式(5)初始化卷尾猴速度,计算其适应度.

5)当步骤4)没有满足条件,根据式(6)更新寿命函数,根据式(8)和(9)更新卷尾猴位置,计算其适应度.

6)重复步骤5),直至达到精度要求或者到达最大迭代次数.

7)得到最优组合,对DBN网络参数设置.

2 实验方法及结果

2.1 实验数据

本文使用的数据集为华东某地区水泥厂2021年11月的负荷实测数据.本实验使用的数据集包括水泥厂二线粉磨车间和二线原料磨车间采集的不同电力负荷的有功功率,对每个负荷每5 min采集一次功率数据,每天共采集288个数据点,每类负荷数据集大小为30×288.负荷包括辊压机(定辊)主电机(S1)、水泥循环风机主电机(S2)、水泥粉磨主电机(S3)、废气处理排风机(S4)、窑尾高温风机(S5)、辊压机(动辊)主电机(S6)共6种负荷装置.其数据波形如图4所示.根据采集信息,水泥厂在7日、8日原料磨车间和粉磨车间轮休进行检修,因此舍弃为0的数据.

2.2 实验方法

2.2.1负荷数据MVMD分解

将每组数据采用MVMD分解.计算每种负荷有功功率数据原始波形与分解后K=3组数据的相关系数ck,如表1所示.

表1 分解信号与原始信号的波形相关系数表

由表1可知,对6种负荷经MVMD分解过程中,K=3时,S1、S3、S4、S5、S6的cmin均小于阈值0.3,即停止分解;S2在K=2时既满足停止条件,为了保证特征向量维度的一致性,方便后续神经网络向量输入,综合取分解分量K=3.取S1负荷观察其分解3层模态分量波形与频谱对应图,如图5所示.由图5可观察,负荷信号S1经3层分解后,其高中低频谱均已被分解出,且没有出现模态混叠的现象,证明所提出的停止准则有效,在多元负荷分类中应用成功.

2.2.2提取特征向量

根据上一小节,将各负荷删减数据为0的数据后,对共29 d的数据MVMD分解,提取各分量特征向量,计算各分量的能量值作为特征,得到特征向量大小为174×3的矩阵,并根据特征向量制作对应标签向量,标签矩阵大小为174×6.

2.2.3CapSA优化DBN网络

根据1.5小节所述,利用CapSA对DBN网络的动量m、学习因子α、以及隐含层RBM1、RBM2的神经元个数寻优.设置CapSA的初始参数如表2.

表2 CapSA 参数设置

设置好参数后,将DBN网络分类误差作为适应度函数,进行参数优化.CapSA优化结果为α=0.994 3,m=0.095 8,RBM1和RBM2的神经元个数分别为15、17.

2.3 实验结果

将由CapSA优化得到的参数,对DBN网络参数设置,输入多元负荷特征向量与标签;其中70%数据作为训练集,30%的数据作为测试集,其分类结果平均正确率在88.89%以上.图6为DBN网络对多元负荷分类结果图,表3为各负荷根据图6分类结果所统计的分类准确度表.

根据图6以及表3的结果可以观察,S6的准确度相比较其他负荷较低,其分类模糊类为S1.根据图4可以明显看出S6与S1的波形相似性很高,数据特征区分度不高,由于整体数据量不够,因此难以准确区分.

为了验证本模型的准确性,采用不同优化算法对DBN参数进行优化,图7为CapSA优化算法与灰狼优化算法(GWO)、飞蛾火焰优化算法(MFO)对DBN参数优化的结果对比图.

表3 各负荷分类准确度

从图7可以明显观察出,CapSA收敛速度更快,在经过17次迭代后,其结果已经达到最优0.111 1,相比于GWO需要41次迭代才能达到最优,其速度更快;MFO误差结果在第17次误差达到最优0.148 1,相对CapSA,其精度低了33.30%.综合比较,CapSA的整体效果最好.

3 结 论

本研究就工业生产中为合理调度用电负荷,对具体负荷的如何准确分类进行讨论.研究结果表明: 1)通过停止准则确定变分模态分解的分解模态分量数,有效避免了传统变分模态分解的分解分量由人为确定的模糊性,使分解分量有依据,适应性更强,减少通过多次实验确定的不准确性同时也能提高分解速度; 2)采用CapSA优化DBN算法,对比GWO、MFO优化结果,CapSA收敛速度更快,较GWO减少迭代时间;优化更加有效,较MFO精度有所提高.但针对负荷曲线相似度高、数据少的负荷分类结果不理想,仍需改进,这是后续需要研究的方向.