三芯矿用电缆线芯温度预测及故障预警方法

王彦文,张旭然,高 彦,王 乐,武灵杰

(1.中国矿业大学(北京) 机电与信息工程学院,北京 100083;2.中国大唐集团科学技术研究院有限公司 华北电力试验研究院,北京 100040)

随着矿山采掘设备装机容量的不断增加,矿用电力电缆的使用量也同步增长,电缆故障的概率相应增大。煤矿井下工况条件复杂,其空间狭小、环境湿度大、设备错综复杂且污浊等级高[1],电力电缆的绝缘容易发生劣化且其散热也会受到煤尘的影响。在煤矿供电事故中,电缆故障的占比超过60%[2-3],而电缆故障最终表现为绝缘劣化甚至失效。电缆运行过程中线芯导体的异常温升是电缆故障的极早期特征[4],高温使电缆绝缘介质发生绝缘劣化,易引发漏电、短路及电缆放炮等故障,进而导致电缆火灾,威胁井下作业人员安全,甚至会引发矿难[5-6]。例如,交联聚乙烯电缆线芯的最高工作温度为90 ℃,当线芯温度高于137 ℃时则可能发生绝缘击穿[7],进而引发电缆内因火灾。因此,准确预测线芯导体的暂态温度是矿用电缆故障预警技术的关键。通过预测线芯导体温度,可以确定电缆内因火灾的报警温度阈值,实现电缆内因火灾预警,达到保护电缆、降低电缆火灾概率和加强煤矿供电系统稳定性的目的。

国内外学者针对矿用电缆故障在线监测方法开展了大量的研究,主要集中在电缆绝缘监测方面。董明[8]运用差分法原理,通过构建桥式电路,搭建了可以精确测量电缆局部放电脉冲信号的在线监测系统,实现了高压电缆绝缘状态在线监测与诊断。赵永梅[9]针对矿用电缆绝缘局部放电的物理现象,在电缆绝缘局部放电等效模型的基础上,研究了局部放电过程中弱信号的去噪方法,提出了基于变分模态分解和小波阈值重构的计算方法,为基于局部放电法的矿用电缆绝缘在线监测技术提供了理论基础。LIU等[10]提出了一种考虑分布电容的快速正负直流叠加电缆在线监测方法,减少了监测时间,避免了水树枝对测量精度的影响。GARRO U等[11]对来自各种传感器的大量局部放电数据进行了前瞻性思考,提出了一种可测量中压电缆、其附件和配电变压器局部放电信号的罗氏线圈优化设计。陈会峰等[12]对比分析了短时傅里叶变换和傅里叶分析去噪法的原理,提出了基于小波阈值的矿用高压电缆的局部放电去噪算法。KUMAZAWA T[13]测量了带有水树枝的电缆的劣化信号,评估了交流叠加电流和交流击穿电压之间的关系,提出交流叠加电流倾向于随着电流的增加而线性增加。谌文佳等[14]通过探测电缆过热释放的特征气体,实现了电缆故障的早期探测。但是,此时绝缘介质已经受到了高温的损坏,后期仍需对故障电缆进行更换。

上述方法主要通过局部放电法、叠加交流法、和检测电缆绝缘介质的热分解产物等方法监测电缆的绝缘状态。但是这些方法不能及时监测到电缆的异常温升,其所监测的特征出现时,电缆绝缘已经劣化。通过监测电缆线芯导体的温度,可对电缆故障进行极早期预警,从而避免电缆自身高温对绝缘的损坏。但是,电缆带电运行状态下,无法直接测量线芯温度,只能由可测量指标来计算线芯导体的温度。付文俊[15]梳理了井下电缆火灾的起因,分析了现有电缆火灾故障的监测方法,提出了一种基于非接触红外缆式线型探测器的煤矿高压电缆温度监测技术,可实时、准确地监测电缆外护套表面温度,为电缆线芯温度预测及故障预警提供了技术参考。运用解析法或者数值法可以由电缆外护套表面温度计算出电缆线芯的温度[16-17]。有学者使用基于数值法的有限元模型求解线芯温度,但是该算法计算量大,且精度会受到结构划分及网格尺寸的影响,不适合工程应用[18]。

笔者基于热路解析法,根据矿用电缆的结构特点和各层材料的参数,计算出热路模型中的热容、热阻,建立了适用于三芯矿用电缆的暂态热路模型算法,并采用分层优化的方法降低了热路模型算法的误差。通过实验验证的方式,证明了优化后的暂态热路模型满足电缆线芯温度预测的需求。达到了由电缆外护套表面温度精确推算线芯导体温度的目的,解决了电缆工作时线芯温度无法直接测量的难题,为三芯矿用电缆线芯温度预测及故障预警提供了理论参考。该算法也为电缆内因火灾预警和报警温度阈值的确定提供了新的思路。

1 三等分暂态热路模型

1.1 三芯矿用电缆结构及其参数

煤矿井下6 kV和10 kV供电线路一般采用中性点不接地或经消弧线圈接地的方式运行,电缆为三芯或多芯形式。其中,三芯电缆径向截面上的三相导体呈“品”字形对称分布,从电缆线芯至外护套表面分别是线芯导体、绝缘层、绝缘屏蔽层、填充物、绕包带、内护套、铠装层和外护套[19]。利用其径向截面上的对称性,将三芯矿用电缆的径向截面等分为3个独立的部分,每部分包含一根完整的芯线截面,如图1所示。本文以MYJV 22-6/6kV-3×50电缆为研究对象,电缆实测参数见表1。

表1 MYJV 22-6/6kV-3×50电缆参数[19]

1.2 三等分热路模型

在电缆径向截面上,线芯导体的温度最高,热量由导体向电缆表皮传递。受结构的影响,电缆表皮各点的温度呈不均匀分布。从图1可以看出,线芯到外护套表面a点的传热路径最短,所以该点处的外护套表面温度最高。将等分后的每一份都等效为单芯电缆,并单独建立线芯至外护套表面a点的暂态热路模型,并计算每份中各层材料的热容与热阻,如图2所示[20-23]。

图1 电缆等分示意Fig.1 Schematic diagram of cable bisection

建模时,忽略不同材料之间的接触热阻和金属材料的热阻,不考虑电缆轴向传热的影响。因为电缆填充层不在最短的传热路径上,所以在建立热路模型时忽略其热阻,只考虑等效热容。

该模型将电缆的每一个物理层都视为集总热容体,忽略了材料内部瞬时温度梯度对热路模型算法计算精度的影响。材料中的热扩散率是衡量材料内部温度变化快慢的指标,热扩散率越小,材料内部温度传播的速率越低,温度梯度越大。

(1)

图2 电力电缆温度场热路模型Fig.2 Thermal circuit model of power cable temperature field

其中,K为材料的热扩散率;γ为材料的导热系数;δ为该层材料的体积热容,J/(K·m3)。热扩散率主要取决于材料自身的参数特性,其与材料导热系数成正比,与体积热容成反比。在非稳态传热中,导热系数低的材料通过的热量低,则材料内部的温度梯度大。同理,体积热容越大的材料,其内部的温度梯度也越大。

1.3 热路模型分层优化

暂态热路模型直接使用同一温度值来表示整个物理层的温度会给模型算法的计算精度带来较大影响。分析可知,材料体积热容是影响温度梯度的重要因素。为了降低电缆材料内部温度梯度的影响,对热扩散率较低,且厚度较大的绝缘层、内护套以及外护套进行等热容分层处理,建立基于分布参数的矿用电缆等热容分层暂态热路模型。

分别将电缆的绝缘层、内护套和外护套分为L层、M层和N层,L、M、N为正整数。等热容分层热路模型如图3所示。其中,C11～C1L为电缆绝缘层各分层热容,J/K;P11～P1L为电缆绝缘层各分层损耗,W;R11～R1L为电缆绝缘层各分层热阻,K·m/W;C″3为填充层及绕包层热容,J/K;R3为电缆绕包层热阻,K·m/W;C41～C4M为电缆内护套各分层热容,J/K;P41～P4M为电缆内护套各分层损耗,W;R41～R4M为电缆内护套各分层热阻,K·m/W;C61～C6N为电缆外护套各分层热容,J/K;P61～P6N为电缆外护套各分层损耗;R61～R6N为电缆外护套各分层热阻,K·m/W。等热容分层时,相同材料的热容值相同。依据材料特性,将分层暂态热路模型进行合并化简,如图4所示(T12～T1L为电缆绝缘层各分层的内表面温度;T41～T4M为电缆内护套各分层的内表面温度;T62～T6N为电缆外护套各分层的内表面温度)。

图4中,C1=C′1+C11,P1=P′1+P11,C3=C′2+C″3,P5=P′4+P61,C5=C′4+C61。根据热路模型与电路相似的特性,对热路模型列节点方程,得到方程组

图3 矿用电力电缆分层热路模型Fig.3 Layered thermal circuit model of mining power cable

图4 矿用电力电缆分层热路模型化简Fig.4 Simplification of layered thermal circuit model of mining power cable

(2)

其中,t为时间。将上述方程组整理成矩阵形式,即

(3)

设初值T(t0)=β,β为初始时刻的温度矩阵,则式(3)的解为

(4)

式中,t0为初始时间;t为时间。

则可以根据电缆外护套表面温度T0,求解出电缆线芯温度T1。其中:

(5)

(6)

(7)

A=

(8)

(9)

(10)

1.4 热路模型参数的计算

笔者利用三芯电力电缆导体的 “品”字形对称分布,将三芯电缆截面做三等分,分割后的每部分包含一根完整的芯线,所以计算分割后的1/3电缆的对应参数。

1.4.1 线芯发热功率

在高于20 ℃的温度下,电缆导体的交流电阻通常由式(11)给出。

R=R′(1+Ys+Yp)

(11)

R′=R0[1+α20(T1-20)]

(12)

式中,R为T1下导体的交流电阻,Ω/m;R′为T1下导体的直流电阻,Ω/m;Ys为趋肤效应因数;Yp为邻近效应因数;R0为20 ℃下导体的直流电阻,Ω/m;α20为线芯导体的温度系数。

(13)

(14)

式中,f为电源频率,Hz;ks为趋肤效应系数经验值,通过查表可得。

(15)

(16)

(17)

其中,dc为导体直径,m;s为各导体轴心之间距离,m;kp为临近效应系数经验值,通过查表可得。单位长度电缆线芯的发热功率P为

P=I2R

(18)

式中,I为单相电流,A。

1.4.2 电缆热阻

根据IEC60287标准,电缆绝缘层材料的热阻Rn为

(19)

式中,ρ为该层热阻率,km/W;d1为该层的内径,m;d2为该层的外径,m。

1.4.3 电缆热容

电缆各层材料的热容C计算式为

(20)

式中,δ为材料的体积热容。

2 实验验证与分析

为了验证三等分等热容分层热路模型算法的准确性,笔者选取型号为MYJV22-6/6kV-3×50的矿用电力电缆为实验对象,研究了电缆外护套表面和电缆线芯温度的变化规律。根据矿用电力电缆的结构特点,设计了电缆接线和温度测量点位的安装方法,制定了实验流程。通过调节负载电流的大小,模拟了电缆正常工作和过电流状态,并记录到电缆线芯导体和其对应的外护套表面的实时温度数据。

2.1 实验系统

电缆温度电流实验平台主要具有三相低压大电流输出和温度测量两大功能,可同时实现0～1 000 A三相低压大电流的稳定输出和-80～+500 ℃的精确测量,实验平台如图5所示。实验平台的升压系统由自动调压器、升流降压变压器和补偿电容组成,如图6所示。测温系统由2组RTD-8型高精度温度记录仪构成,并采用热电偶作为测温传感器,支持16路温度信息的实时采集。

图5 电缆温度电流实验平台Fig.5 Photo of cable temperature and current experiment platform

本实验中,将被试电缆的3根芯线视为纯电阻,采用星形接法与实验平台的大电流输出端相连接。

图6 电缆温度电流实验平台升流模块系统Fig.6 System diagram of current rising module of cable temperature and current experimental platform

为了准确测量线芯导体的温度,分别在3根芯线对应的位置打孔,直至暴露导体,然后在涂抹导热硅脂后使传感器与导体紧密接触并用电工胶带固定。因为电缆线芯到电缆外护套表面各个点位的热传导路径有所不同,所以电缆外护套表面的温度分布不均匀,选取3根芯线所对应的最短传热路径上的外护套表面粘贴热电偶,测量其外护套表面温度[24]。热电偶安装情况如图7所示。

图7 热电偶安装Fig.7 Thermocouple installation drawing

2.2 实验过程

采用100、200和320 A的三相平衡阶跃电流进行连续实验,模拟矿用电力电缆正常工作和过流工况,以测量电缆线芯和其对应的外护套表面的温度。实验环境温度为25 ℃。被试电缆的绝缘材料为交联聚乙烯,故本实验中设定90 ℃为电缆线芯的最高工作温度,设定137 ℃为电缆故障的预警温度。实验中,首先以100 A的实验电流模拟电缆正常工作状态,然后分别以200、320 A两个阶跃电流模拟电缆的故障电流。

实验电流为100 A时,电缆开始升温,线芯的温升速率高于外护套表面。实验持续1 h后,被试电缆温度趋于平稳。然后,分2次将电缆温度电流实验平台的输出电流值调整为200和320 A,模拟电缆的故障工况。电缆持续升温,温度逐渐超过最高工作温度90 ℃。当测得电缆线芯温度达到137 ℃后,停止实验。实验中模拟电流的大小如图8所示。将各个热电偶测量的温度数据进行分析整合,作为电缆线芯温度与外护套表面温度值,线芯温度和电缆外护套表面温度变化如图9所示。

图8 电缆电流曲线Fig.8 Cable current curve

图9 电缆线芯温度与外护套表面温度变化曲线Fig.9 Change curves of cables core temperature and skin temperature

2.3 数据处理及对比验证

在等热容分层暂态热路模型损耗计算中,只考虑电缆线芯、绝缘层、绝缘屏蔽层以及铠装层的损耗。电缆填充层、绕包层、内护套、铠装层、外护套的热容以及铠装层损耗为计算值的1/3。采用控制变量法,依次对电缆的绝缘层、内护套以及外护套进行10、20、30、40、50和60层等热容分层计算,并与实验中320 A模拟过电流的线芯实测温度进行对比,分析不同分层数对热路模型计算结果的影响,如图10～12所示。

图10 电缆线芯温度计算值随绝缘层分层数变化Fig.10 Variation of calculated value of cable core temperature with the number of insulation layers

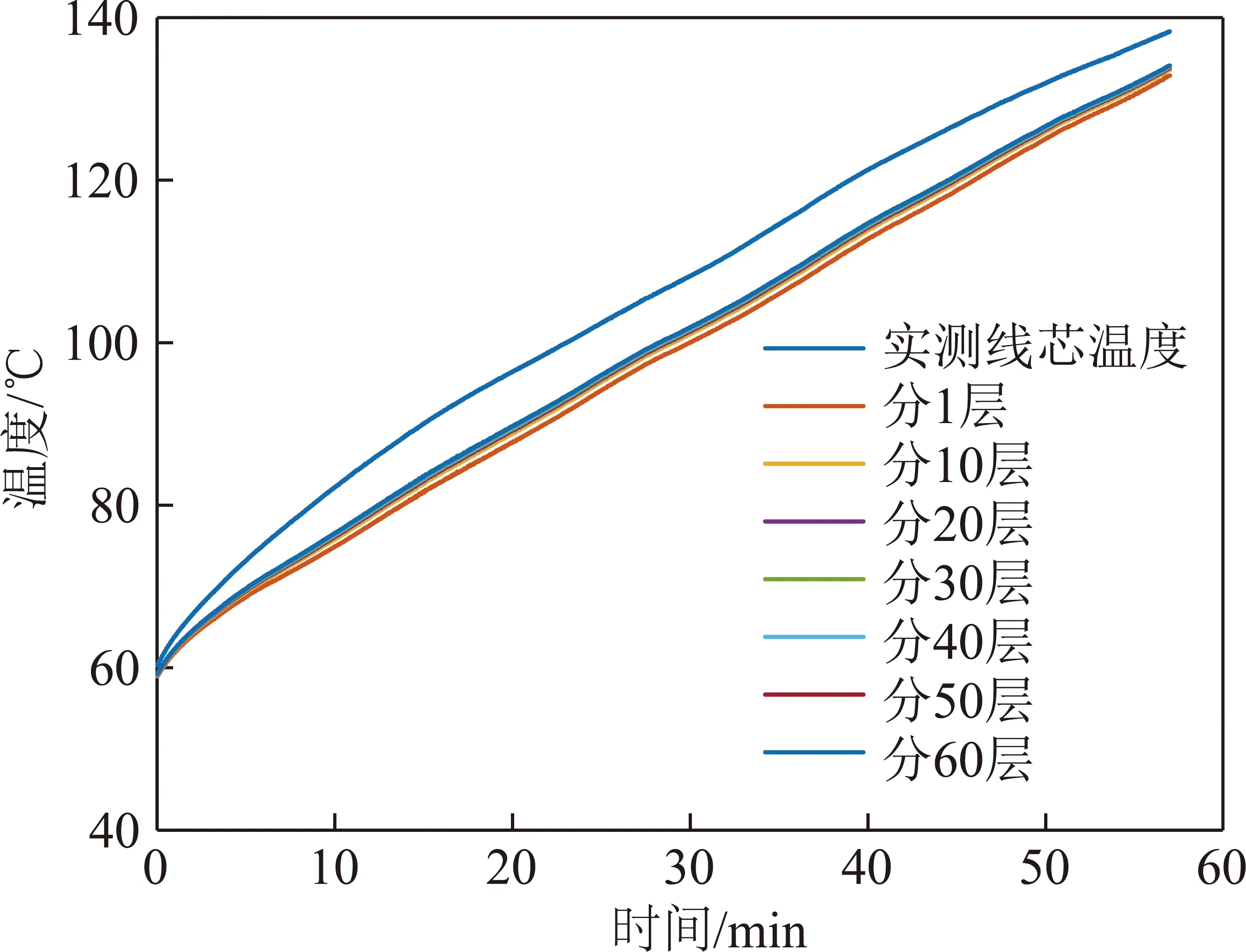
图11 电缆线芯温度计算值随内护套层分层数变化Fig.11 Variation of calculated value of cable core temperature with the number of layers of inner sheath

图12 电缆线芯温度计算值随外护套层分层数变化Fig.12 Variation of calculated value of cable core temperature with the number of layers of outer sheath

从图10～12可以看出,随着各层材料分层数的增加,模型的计算结果不断向实验测量值趋近,绝缘层分层时计算值向测量值的趋近程度最强。这是因为电缆绝缘层最靠近电缆线芯热源,内部的温度梯度最大,故其分层对模型计算精度的影响也强于内护套和外护套。上述数据还表明,随着分层数越大,计算值向测量值的趋紧速度变缓。对电缆线芯温度计算值随各层材料分层的计算精度进行归纳,分析该分层数下相对于上一级分层计算精度的增加值,如图13所示。

图13 计算精度增加值随分层数变化Fig.13 Variation chart of calculation accuracy growth value with the number of layers

由图13可以看出,对电缆进行等热容分层优化能有效降低暂态热路模型的计算误差,电缆绝缘层分层对热路模型计算精度的影响大于其他2层。当分层数达到50层后,计算精度的增加值小于0.1 ℃。因为实验中热电偶的测量精度为±0.1 ℃,所以分层数达到50层后计算精度增加值小于传感器的测量精度,误差分析失去意义。所以被试矿用电缆绝缘层、内护套和外护套等热容分层优化的最佳分层数均为50层。将矿用电缆绝缘层、内护套以及外护套的分层数L=50、M=50、N=50代入3等分等热容分层暂态热路模型,并将线芯温度的计算结果与实验测量值做误差分析。线芯温度计算值的最大相对误差小于1%,平均相对误差为0.73%,满足电缆线芯温度预测及故障预警的计算要求。

3 结 论

(1)根据电缆线芯异常温升这一电缆故障的极早期特征,提出了通过监测电缆外护套表面温度推算电缆线芯温度,从而实现电缆线芯温度预测及故障预警的方法;依据所研究三芯矿用电缆径向截面的结构特点,构建了适用于三芯矿用电缆线芯导体温度计算的三等分暂态热路模型算法,找到了电缆内因火灾预警、报警温度阈值的确定方法。

(2)以MYJV22-6/6kV-3×50三芯矿用电缆为研究对象,针对电缆故障的极早期阶段进行了电缆温度电流实验,分析验证了三等分暂态热路模型算法,发现电缆绝缘材料内温度梯度是影响模型计算精度的重要因素,对电缆材料进行等热容分层优化可以提高计算精度。

(3)当电缆材料的等热容分层数达到一定量级后,再增加分层数对模型计算精度的提升效果有限,反而会增加计算量。本文中电缆绝缘层、内护套以及外护套的等热容分层数均为50时,模型计算值的最大相对误差小于1%,平均相对误差为0.73%,可为进一步研究其他种类的矿用电缆线芯温度预测和故障预警方法提供理论参考。