基于K-Means聚类与凸包检测的金刚石磨粒分割与评价*
2023-05-19李弘扬方从富
李弘扬,方从富
(华侨大学 机电及自动化学院,福建 厦门 361021)
金刚石是自然界已知最硬的物质,因其优良的物理化学性能被广泛应用于磨削、研磨和抛光等加工领域[1]。在金刚石工具的使用过程中,金刚石的形状轮廓、位置分布、磨粒数量以及出刃状态等特征是影响工具性能以及加工结果的重要因素[2]。因此,深入研究磨粒特征参数具有重要意义,而基于数字图像的磨粒分割和特征提取技术则提供了可能性。
随着计算机技术的不断发展,图像处理技术已逐渐用于磨粒特征的分割和提取,并且已经取得了一定的优秀成果。张秀芳等[3]利用图像增强、二值化等图像处理技术对金刚石磨粒进行分割,通过将金刚石颗粒等效成规则多边形实现了金刚石粒度的测量。李银华等[4]利用图像处理技术提取了金刚石磨粒的体积参数,并依据该特征参数建立一个多元回归函数模型,实现了金刚石颗粒的体积计算与分析,其结果具有较高的准确率。吴文艺等[5]提出基于二次灰度直方图的图像处理方法对砂轮表面的金刚石磨粒进行提取,并将该方法与Ostu 算法、贝叶斯算法、Canny 算子的分割结果进行了对比,结果表明通过该方法分割提取的磨粒轮廓更完整。杨栖凤等[6]利用基于机器视觉的测量方法对砂轮表面的二维形貌进行全场测量,结合图像处理技术对磨粒进行分割提取,最终获得了金刚石砂轮表面磨粒数量、磨粒粒径以及位置信息等参数。潘秉锁等[7]利用空洞卷积网络对金刚石磨粒图像进行语义分割,通过优化分割模型的超参数实现了较好的分割结果。LIN 等[8-9]利用基于形态学与边缘检测的图像处理技术对磨粒进行分割提取,较为完整地提取了磨粒图像,且分割误差为5.7%~10.9%。PAN 等[10]利用基于Otsu 阈值分割、均值偏移以及图像纹理的方法对金刚石磨粒进行分割提取,最终实现了金刚石磨粒的三维重建。赵玉康等[11]利用多相机协同采集金刚石线锯的表面图像,结合图像处理技术实现了图像的拼接与裁剪,最终得到了磨粒的分割结果,该方法的分割精度比传统的单相机采集方法高17.3%。KANG 等[12]对磨粒进行识别、分割与标记,提取了磨粒的形状,并定义参数实现了砂轮表面磨粒特征的提取。上述这些研究成果为金刚石磨粒分割提供了良好的借鉴意义,也为金刚石磨粒的特征提取等打下了良好的基础。但是,磨粒粒度、结合剂种类以及磨粒与结合剂的不同黏结方式和黏结条件会使工具表面呈现出复杂的轮廓特征,在不同的条件下采集图像也可能会增加磨粒图像的干扰信息。因此,复杂背景下的磨粒图像分割一直是磨粒分割提取的难点问题。
近年来,基于K-Means聚类的图像分割技术在很多领域都有应用,如自然场景以及遥感、雷达图像的分割等[13-15]。该算法是基于样本集合划分的聚类算法,在一定程度上可以减少复杂背景轮廓对目标分割的影响,从而有效实现目标的提取。另外,对于传统分割方法中部分目标区域存在黏连现象的问题,学者们常用凸包检测的方法对黏连区域进行分割,从而使黏连区域相互分离[16-17]。
基于以上研究现状,针对复杂背景以及强干扰情况下的金刚石磨粒图像分割困难等问题,提出一种基于K-Means聚类(K-means clustering)与凸包检测(Convex hull detection)的磨粒分割方法(KM-CHD)。通过该方法实现磨粒的分割提取,并对磨粒分割结果进行评价。
1 金刚石磨粒图像的采集与分割
1.1 图像采集装置
为获取较为清晰的磨粒图像,磨粒图像采集工作在三维视频显微镜测量系统(Hirox KH-8700)上进行,如图1所示。该设备的放大倍数为35~2 500 倍,采集的图像尺寸为1 600 Pix × 1 200 Pix。试验时,调整显微镜放大倍数使基底面成像清晰,并采集磨粒图像。采集的磨粒图像如图2所示。

图1 三维视频显微镜图像采集系统Fig.1 3D video microscope image acquisition system

图2 典型磨粒图像Fig.2 Typical abrasive grain image
1.2 磨粒图像分割
1.2.1 图像处理平台
数字图像处理程序在Pycharm2019(Python3.7)软件平台运行,硬件平台为双核i7-4700MQ(2.4 GHz)处理器和8 GB(1 066 MHz)内存的戴尔工作站。
1.2.2 基于K-Means聚类的预分割
由于采集的图像带有噪声,这些噪声会对图像的特征提取产生负面影响,因此需要对图像进行滤波操作。高斯滤波是常用的滤波方法,能够有效地滤除图像的部分噪声。设原始图像为I(x,y),高斯核为Gσ,通过卷积运算得到滤波后的图像f(x,y)为:
由于金刚石具有十分复杂的晶体结构,这就会导致其形态特征极为多样。基于图2所示的磨粒的二维图像,可以看出磨粒与结合剂之间存在较为明显的色差,磨粒区域与结合剂之间的色差种类不同。为了能够提取完整的磨粒轮廓,需要将磨粒与结合剂分类,从而实现磨粒轮廓的提取。
设图像f尺寸为M×N,为了初始化模型,在图像中随机选取K个聚类中心μ,每一个聚类中心对应相应的像素值簇。当确定了K个聚类中心时,就产生了K个簇C,初始条件下C均为空集:
其中:ξ=1,2,3,···,K。本文K取4。
然后计算每个像素值与聚类中心之间的欧氏距离,并进行迭代。当畸变函数的值最小时,聚类结束。对于图像中任意一点的像素值fi,计算与每一个聚类中心的距离dξ,当dξ取最小值时,fi就归为簇Cξ,随即更新Cξ。
其中:i=1,2,3,···,MN。
假设簇Cξ有m个元素,对所获取的簇再重新计算聚类中心,得到新的聚类中心μξ,重复上述操作,使畸变函数J取得最小值。最终得到K个聚类中心和最终的聚类结果。为了区分图像中的不同簇,令归属簇Cξ的所有值统一为聚类中心的值,最终得到聚类后的图像:
其中:fi∈Cξ
通过K-Means聚类算法对磨粒图像进行聚类以突出显示磨粒区域的主要轮廓,图像聚类预分割的结果如图3所示。
1.2.3 基于凸包检测的精分割
由于金刚石磨粒图像中包含了较多的背景噪声,K-Means聚类可以将图像复杂的灰度范围规范在几个固定的灰度。为了更完整地提取磨粒区域,对聚类后的图像进行二值化与形态学处理等操作。目的是增强背景与磨粒区域的对比度并且消除细小轮廓,结果如图4 和图5所示。然后,进行磨粒区域的主轮廓提取,目的是避开复杂的背景轮廓,并提取磨粒轮廓。
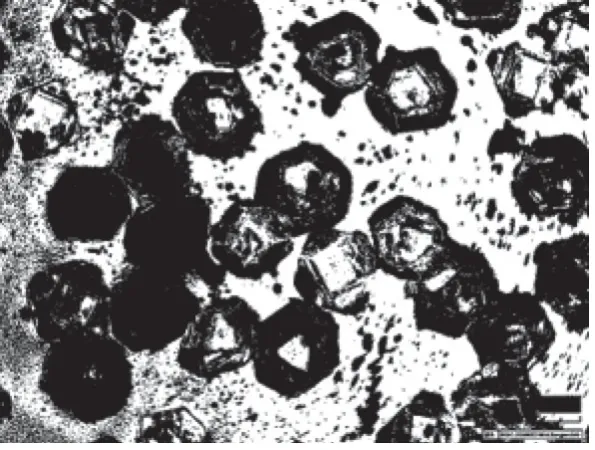
图4 磨粒图像的二值化结果Fig.4 Binarization results of abrasive grain images

图5 磨粒图像的形态学处理结果Fig.5 Morphological processing results of abrasive grain images
但是,经过二值化与形态学处理之后的图像依然存在较多的空洞和黏连。因此,在精细分割之前需要将空洞填充,填充结果如图6所示(图4,图5 与图6的标尺均与图3 一致)。图6 中填充后的图像,磨粒之间存在较多的黏连。为将磨粒分割成独立的区域,对填充后的磨粒图像进行凸包检测,目的是找到凸缺陷以确定黏连磨粒的分割点。首先,确定凸包的起始点P0,这里设置磨粒边缘纵坐标最小的点为凸包的起始点,寻找靠近P0且顺时针转角最小的点P1;连接P0、P1,形成凸包的第一条轮廓线;并以得到的P1作为新的起始点,寻找下一个凸点,重复以上步骤直至找出所有凸点。将所有的凸点连接,即可得到最终的完整凸包,如图7所示。

图6 空洞填充结果Fig.6 Hole filling results
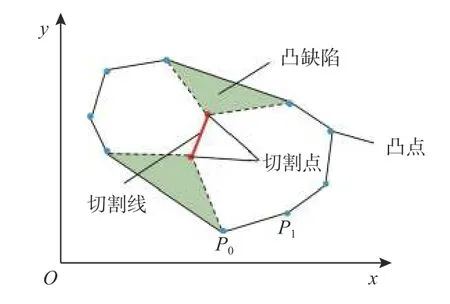
图7 凸包检测与生成示意图Fig.7 Schematic diagram of convex hull detection and generation
得到的凸包轮廓与磨粒的实际轮廓存在较大差异,因磨粒与凸包之间存在不同程度的凸缺陷。选取最大的2 个凸缺陷并寻找2 个凸缺陷之间的最邻近点作为切割点,并设置切割线将黏连磨粒完全分离,如图8所示。
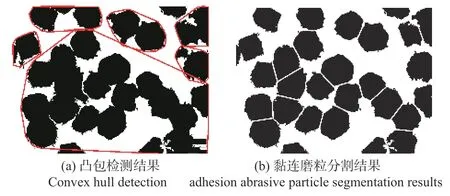
图8 凸包检测结果及黏连磨粒分割结果示意图Fig.8 Schematic diagram of convex hull detection results and adhesion abrasive particle segmentation results
1.3 分割效果评价指标
为了比较KM-CHD 方法的分割效果,利用Adobe Photoshop 软件进行手动分割并将手动分割的结果作为参考,然后将KM-CHD 方法的分割结果与手动分割的结果进行对比。为了全面说明该方法的分割性能,对磨粒轮廓面积精度(ηCAA)、磨粒位置误差(θPE)和磨粒数量召回率(σQR)3 个参数进行评价。
1.3.1 磨粒轮廓面积精度
磨粒轮廓面积是评价磨粒特征的一个重要参数,因此轮廓面积精度也是评价磨粒分割方法的重要指标。设手动分割的磨粒轮廓磨粒面积为Sm,KM-CHD 方法分割的磨粒面积为Sa。图像中的磨粒轮廓面积S可表示为:
其中:f(i,j)为像素值,MN为图像尺寸。
从而,可以得到磨粒轮廓面积精度ηCAA为:
1.3.2 磨粒位置误差
实际上,完全精确计算磨粒的位置是十分困难的,几乎所有的磨粒分割方法都存在或多或少的误差。为了表达这种误差,将手动分割的结果与KM-CHD 方法的分割结果进行对比,计算2 种分割结果的质心坐标。设图像F1在(x,y)处的灰度为F1(x,y),磨粒轮廓的质心坐标(xp,yp)计算过程为:
设手动分割结果的质心坐标为(xm,ym),KM-CHD方法分割结果的质心坐标为(xa,ya),手动分割区域的当量圆半径为R,从而得到磨粒位置误差θPE为:
1.3.3 磨粒数量召回率
利用图像处理方法对磨粒数量进行计数时可能存在一定的少计或多计的问题,尤其是在磨粒数量较多、磨粒黏连以及背景复杂等情况下更容易出现类似现象。因此,为评价KM-CHD 方法在磨粒数量计算方面的性能,对磨粒数量召回率σQR进行计算。
式中:Na为KM-CHD 方法的计数结果,Nm为手动分割的计数结果。
2 结果与分析
通过K-Means聚类预分割与基于凸包检测的精分割过程可以将磨粒区域分割出来。图9 为分割效果图。如图9所示,可以发现利用KM-CHD 方法的分割结果与手动分割结果具有较高的一致性。为了定量评价磨粒分割的效果,选择如图10 和图11所示的4 幅使用前和使用后的工具表面磨粒图像进行对比,进一步对所提出的3 个指标进行分析。

图9 分割效果图Fig.9 Segmentation effect diagram
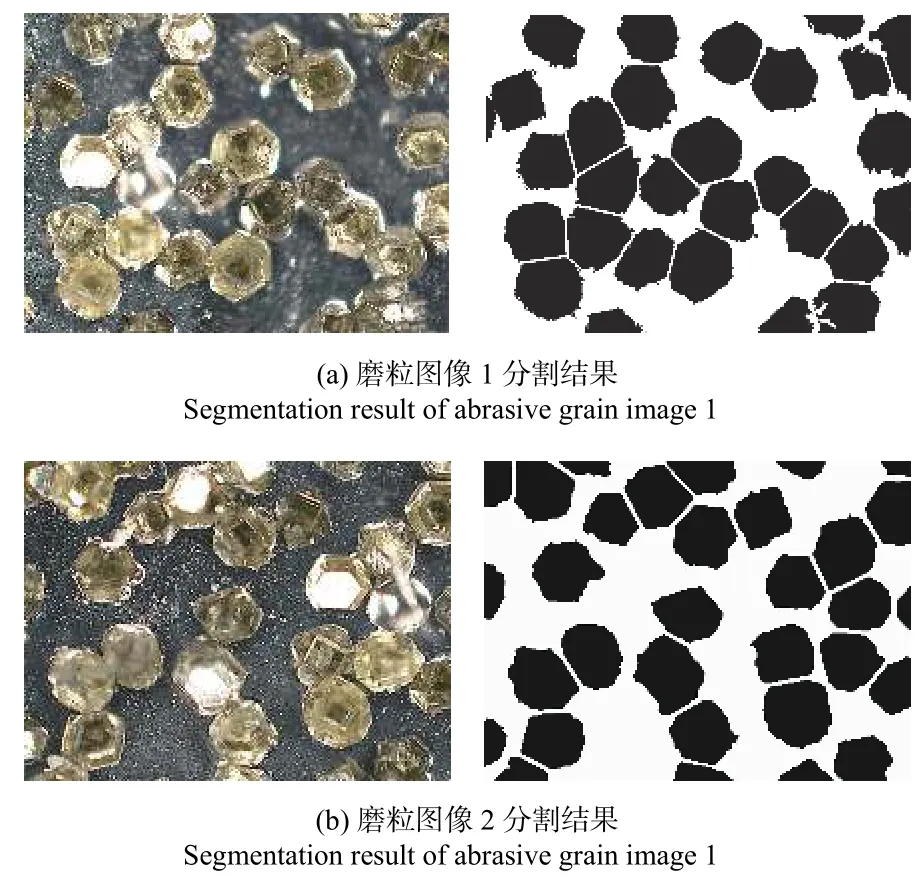
图10 使用前磨粒图像及其KM-CHD 分割结果Fig.10 Image of abrasive grains before use and its KM-CHD segmentation results

图11 使用后磨粒图像及其KM-CHD 分割结果Fig.11 Image of abrasive grains after use and its KM-CHD segmentation results
2.1 磨粒轮廓面积精度
对于金刚石工具而言,磨粒轮廓区域被分割以后与原始的磨粒轮廓区域的形状可能存在不同程度的差异,这就导致了分割结果的有效面积与实际面积之间存在相应的误差。为了比较KM-CHD 方法与手动分割结果在磨粒轮廓面积计算上的差异,对磨粒轮廓面积精度进行计算和分析。图12 为KM-CHD 方法的分割结果。
如图12a所示:随机选择图10 中的磨粒图像1 进行分析,通过对图像中的28 颗磨粒进行面积计算和分析,得到KM-CHD 方法的分割结果与手动分割的磨粒轮廓面积之间具有较高的一致性,两者之间的差异较小。如图12b所示:KM-CHD 方法的轮廓面积精度最大可达99.27%,平均精度达到了95.01%,这个结果表明KM-CHD 方法得到的分割结果与实际的磨粒区域具有较高的吻合度。
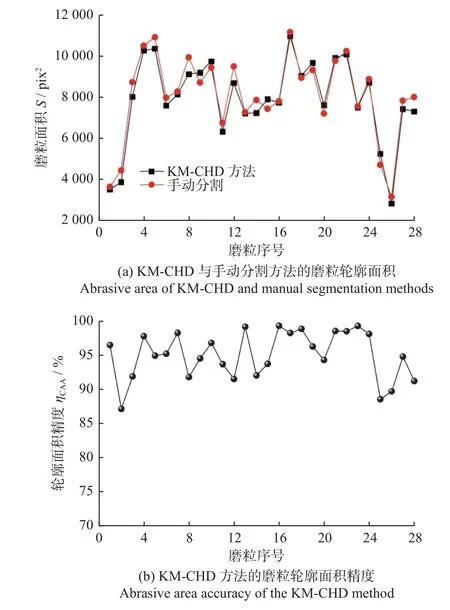
图12 使用前磨粒图像基于KM-CHD 方法的分割面积以及面积精度Fig.12 Segmentation area and area accuracy of unused abrasive image based on KM-CHD method
但是,对使用后的金刚石工具而言,图像的背景更加复杂,分割出来的磨粒区域轮廓具有较多的复杂纹路,且轮廓边缘也并不平滑。图13 为使用后磨粒图像基于KM-CHD 方法的分割面积以及面积精度,如图13a所示:随机选择图11 中的磨粒图像2 进行分析,可以看出,利用KM-CHD 方法得到的磨粒面积绝大部分是与手动分割的结果一致,但是也存在少量磨粒的提取结果与手动分割的结果存在一定的差异。如图13b所示:KM-CHD 方法的轮廓面积精度最大可达97.56%,平均精度达到了81.68%,这个结果表明KM-CHD 方法得到的分割结果与实际的磨粒区域具有较好的吻合度。
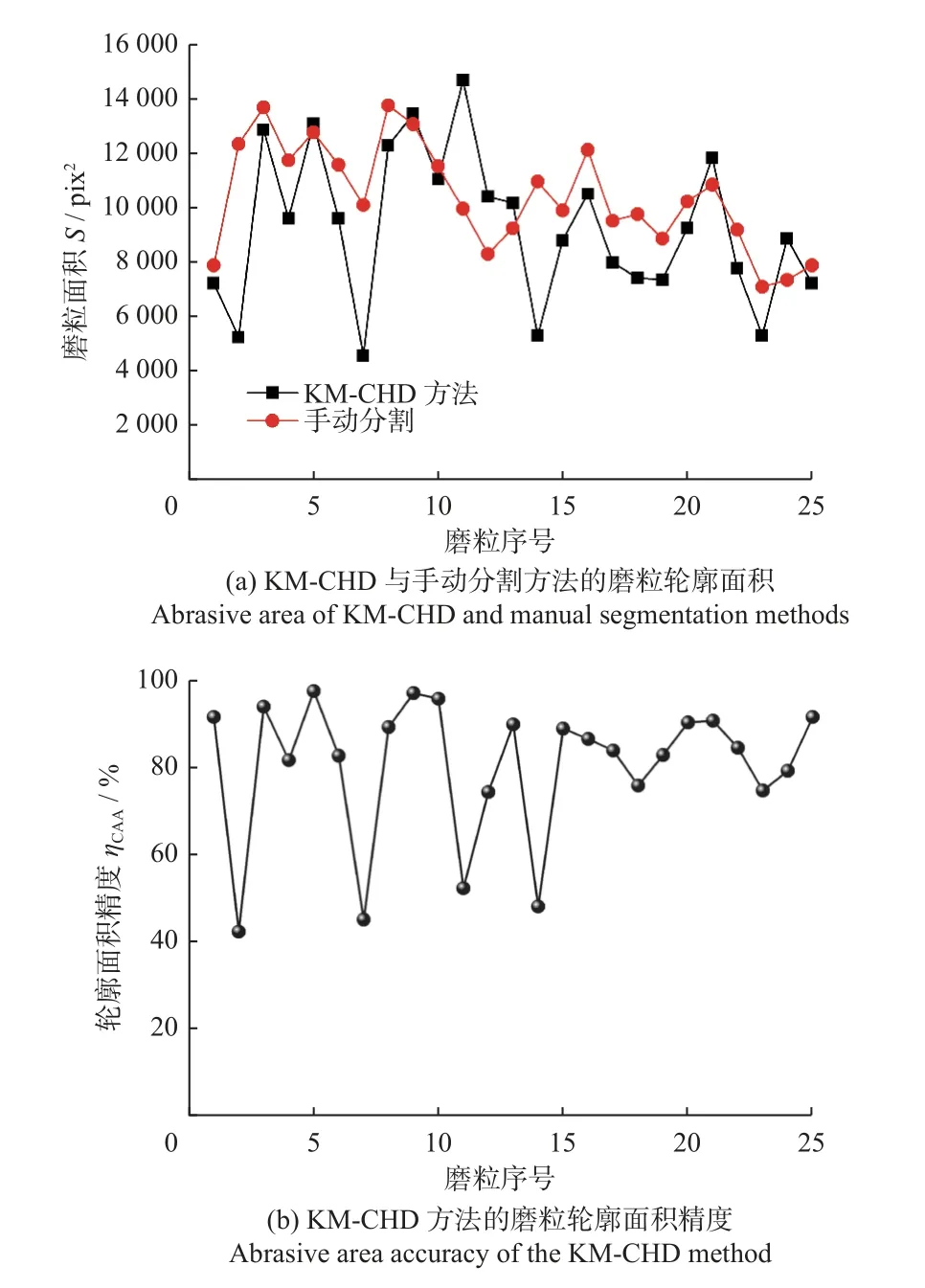
图13 使用后磨粒图像基于KM-CHD 方法的分割面积以及面积精度Fig.13 Segmentation area and area accuracy of used abrasive image based on KM-CHD method
2.2 磨粒位置误差
位置误差表达了分割结果与实际磨粒位置的差异,也是评价分割结果的一个重要指标。图14 为使用前磨粒图像基于KM-CHD方法与手动分割磨粒质心图,如图14所示:对于加工前的金刚石工具表面图像而言,对比手动分割与KM-CHD 方法的分割结果可以看出,对应磨粒的质心的位置差异不大。为比较两者差异程度,求出手动分割轮廓的当量圆半径。
如图15所示,对图14 中的单幅图像中的28 颗磨粒分别进行位置误差的计算。结果表明:KM-CHD 方法所得到的磨粒区域的位置误差最低为0.48%,平均误差为2.93%。

图14 使用前磨粒图像基于KM-CHD 方法与手动分割的磨粒质心图Fig.14 The centroid of unused abrasives image segmented by the KM-CHD method and the manual method
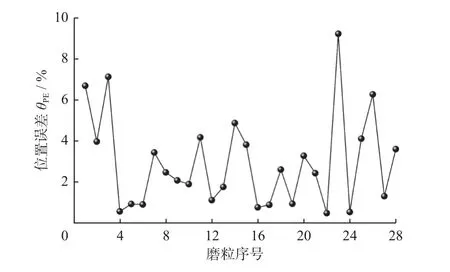
图15 使用前磨粒图像分割的位置误差Fig.15 Position error of unused abrasive image segmentation
图16 为使用后磨粒图像基于KM-CHD 方法与手动分割磨粒质心图。如图16所示:对于使用后的金刚石工具表面图像而言,对比手动分割与KM-CHD 方法的分割结果可以看出对应磨粒的质心的位置具有一定的差异,但是这种差异并不是十分明显。图17 为使用后磨粒图像分割的位置误差,如图17所示:对图16 中的25 颗磨粒分别进行位置误差的计算,结果表明:KMCHD 方法所得到的磨粒区域的位置误差最低为0.84%,平均误差为7.60%。

图16 使用后磨粒图像基于KM-CHD 方法与手动分割磨粒质心图Fig.16 The centroid of used abrasives image segmented by the KM-CHD method and the manual method
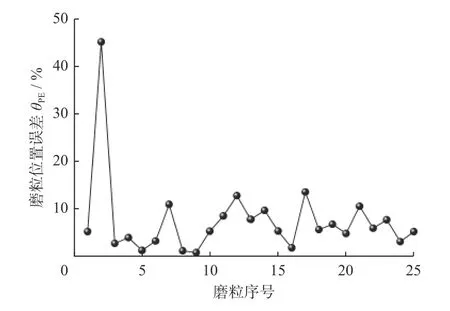
图17 使用后磨粒图像分割的位置误差Fig.17 Position error of used abrasive image segmentation
基于对使用前后的磨粒图像的分割和磨粒位置的提取,说明KM-CHD 方法能够准确定位磨粒的位置。这为磨粒的定位以及磨粒分布的计算提供了参考。
2.3 磨粒数量召回率
磨粒数量召回率表达了基于KM-CHD 方法的磨粒数量统计结果与实际磨粒数量统计结果之间的吻合程度。对图10 和图11 中的4 幅图像(按顺序命名为1,2,3,4)分别利用KM-CHD 方法进行分割,计算相应的磨粒数量,并与原磨粒图像中手动分割的磨粒数量进行比较。
图18 为磨粒数量计算结果。如图18a所示:利用KM-CHD 方法与手动分割的方法对4 幅磨粒图像进行磨粒数量的统计。经过对比,利用KM-CHD 方法得到的磨粒数量与手动分割数量十分吻合。如图18b所示,以手动分割的结果为参考,利用KM-CHD 方法得到的磨粒数量召回率均在96.42%以上,最大达到了100.00%,平均召回率为98.30%。这个结果说明KM-CHD 方法可以有效地用于磨粒数量统计,并且具有较高的召回率。
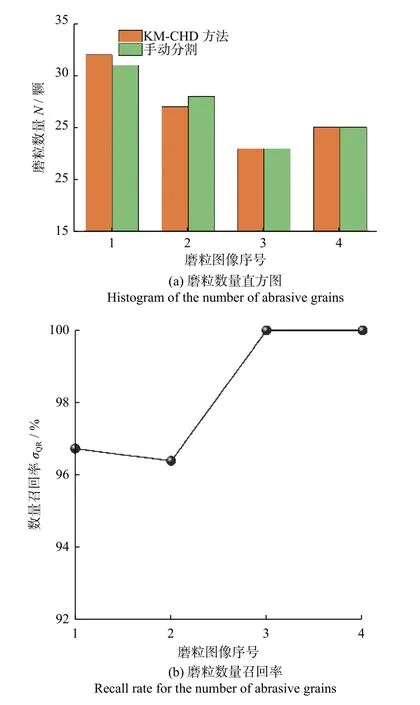
图18 磨粒数量计算结果Fig.18 Calculation results of the number of abrasive particles
基于以上结论,提出的基于K-Means聚类与凸包检测的磨粒图像分割方法在磨粒轮廓面积精度、磨粒位置误差以及磨粒数量召回率3 个参数上表现优良。
3 结论
提出了基于K-Means聚类与凸包的分割方法,结合二值化、形态学等处理方法实现磨粒区域的分割提取。将该方法的分割结果与手动分割结果进行比较和分析,提出磨粒轮廓面积精度、磨粒位置误差以及磨粒数量召回率3 个评价指标对分割结果进行分析和评价。结果表明:提出的磨粒分割方法对于使用前后的金刚石工具表面图像的磨粒分割提取,在面积精度、位置提取以及数量统计方面均表现出较好的性能。
