基于SPH方法的钢筋混凝土切削模拟研究*
2023-05-19谭松成石恒超王伟雄方小红段隆臣
谭松成,石恒超,王伟雄,方小红,段隆臣
(中国地质大学(武汉)工程学院,武汉 430074)
金刚石切削工具具有切割精度高、速度快、振动幅度小的特点,以锯片、串珠和钻头等形式已广泛应用于道路、桥梁、大坝、房屋等钢筋混凝土结构的修复或拆除工作中,并表现出优异的性能[1-5]。为进一步提高金刚石工具的工作效率,需要不断调整工具结构特征、胎体成分和金刚石参数[6-7],并建立合理的切削模型对切削过程进行预测[8],从而选择更优的加工参数,提高工具的综合使用性能。通过合理的物理试验方法能够提高金刚石工具的使用性能,但传统试验方法成本高、周期长,难以及时改变金刚石工具的各项参数进行试验,因此数值模拟已成为一种非常重要的研究方法。
目前有关切削具破岩过程的常见数值仿真方法包括有限差分元法[9],有限元法[10],离散元法[11]和边界元法[12]等,然而关于金刚石切削破碎岩石和(钢筋)混凝土的研究仍然以有限元为主。陈昌雄[13]和刘会宁[14]采用ANSYS 软件的静力学和动力学模态分析,研究了金刚石圆锯片工作过程中的应力应变特征和振型特征,以寻求提高金刚石锯片结构刚度、延长锯片受用寿命的结构参数;鞠军伟[15]和叶鲁浩[16]采用有限元法和边界元法联合仿真的方法对金刚石锯片切削岩石的振动和声辐射特性进行了研究,从而提出低噪音金刚石圆锯片的结构设计方案;张林中[17]采用ANSYS/LS-DYNA研究了单颗粒金刚石在不同出露高度、切削深度和切削速度条件下切削岩石过程中的受力状态变化;肖月[18]基于AdvanEdge 仿真软件建立了金刚石绳锯的单颗粒切削钢筋混凝土的几何模型,研究了不同冷却方式对切削热的影响情况;茹聪[19]采用ABAQUS 建立金刚石单磨粒切削钢筋混凝土的仿真模型,分析了切削速度和切削深度对金刚石切削力及疲劳寿命的影响;孙永泉[20]采用LAMMPS 建立了金刚石颗粒切削金属铁的分子动力学仿真模型,研究了金刚石刀具前、后刀面预制裂纹和金刚石晶面取向对切削温度和切削应力的影响。
上述数值仿真方法在一定程度上能够对切削过程进行还原,但各种数值模型之间无法统一,每种模型都存在一定的局限性。例如在岩石的切削模拟上,边界元法和有限差分元法虽然能够模拟切削过程中岩石内部的裂纹延伸情况,但无法模拟碎屑的形成过程。而有限元法和离散元法虽然能够模拟岩石内部裂纹的延伸情况和碎屑的形成,但有限元法在模拟岩石破碎的大变形过程中会导致网格退化和畸变等问题,从而无法还原真实的切削情况;离散元法在模拟岩石破碎过程时,数值岩样内部不会产生岩石密度、模量等物理性质的变化,但实际切削过程中岩石内部的密度会不断发生变化,导致模拟存在误差。因此,各种数值模拟方法需要进一步的完善。
光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法[21-22]成功将材料粒子的质量和密度引入其本构方程中,可以有效计算切削过程中的压缩问题。同时,由于SPH方法采用的是粒子划分的方法,能够有效避免网格畸变和退化等问题,因此能够有效实现高能、大变形问题的数值模拟[23]。
本文中选用SPH 方法对钢筋混凝土这一非均质材料的切削过程进行模拟,采用方形磨粒和圆形磨粒分别对应孕镶金刚石工具出刃时所出现的面接触形态和多棱角点接触形态,研究了混凝土和钢筋材料切削过程中的形态变化和磨粒表面的应力分布,并对不同形状磨粒的切削应力和切削效率进行比较,探究磨粒形状对非均质材料切削过程的影响。
1 数值模拟参数
Autodyn 显示有限分析单元可用于模拟切削过程中碎屑的形状、磨粒应力应变和基体裂纹扩展与残余应力等效应。实际切削过程中磨粒的尺寸极小,远小于被切削材料表面的棱角尺寸,导致基体在进行建模时不需要考虑实际表面复杂的形状。因此,将钢筋混凝土建模成简单块状体时也能反映实际的切削情况。同时,建模过程中也需要满足切削时能够在基体内部形成不因尺寸限制的完整裂纹,因此磨粒尺寸和基体尺寸需要具有合适的比例。
本次模拟主要考虑基体在切削过程中的变化情况,而磨粒变形相比于基体变形可忽略不计。因此,磨粒建模为刚体,而基体建模为变形体,磨粒和基体之间采用SPH 和拉格朗日接触模型。在数值建模中,基体为5 mm × 3 mm 的矩形块,使用SPH 粒子单元,单元的尺寸为0.075 mm × 0.075 mm;磨粒分别为直径0.25 mm 的圆形和0.25 mm × 0.25 mm 的方形块,使用2D 拉格朗日单元,单元网格的尺寸为0.05 mm×0.05 mm;磨粒的切削深度为0.1 mm。应用于有限单元的边界条件如下:(1)速度边界限制,磨粒水平方向的速度为0.45 mm/ms,垂直方向上的速度为0;(2)基体下边界和右边界上的水平速度和垂直速度均为0。
钢筋作为一种常用的塑性金属材料,在数值模拟中一般采用Johnson-Cook 模型[24]。Johnson-Cook 模型可用于模拟金属材料在大应变、高应变率和高温下的强度行为和失效行为。在此模型中,材料的屈服应力随应变、应变速率和温度的变化而变化。其中,屈服应力Y定义为:
式中:εp为有效塑性应变;为标准有效塑性应变速率;温度比TH=(T-Troom)/(Tmelt-Troom);A、B、C、n和m为材料常数。
Johnson-Cook 失效模型的表达式定义如式(2)、式(3)所示,钢筋所采用的模型参数如表1所示。
式中:ΔεP为积分循环期间的塑性应变;εf为塑性应变;D1,D2,D3,D4,D5为损伤常数;实际等效应力σ*=σ/σHEL,其中 σ为实际应力,σHEL为在HEL 条件下的等效应力;无量纲应变率ε˙*= ε˙/ε˙0,其中 ε˙是实际应变率,参考应变率ε˙0=1.0 s-1;等效温度T*=T/THEL,其中T为实际温度,THEL为在HEL 条件下的等效温度。
混凝土为脆性材料,宜采用D-P 模型[25],其简化的加载曲线如图1所示,分段D-P 强度模型参数如表2所示。
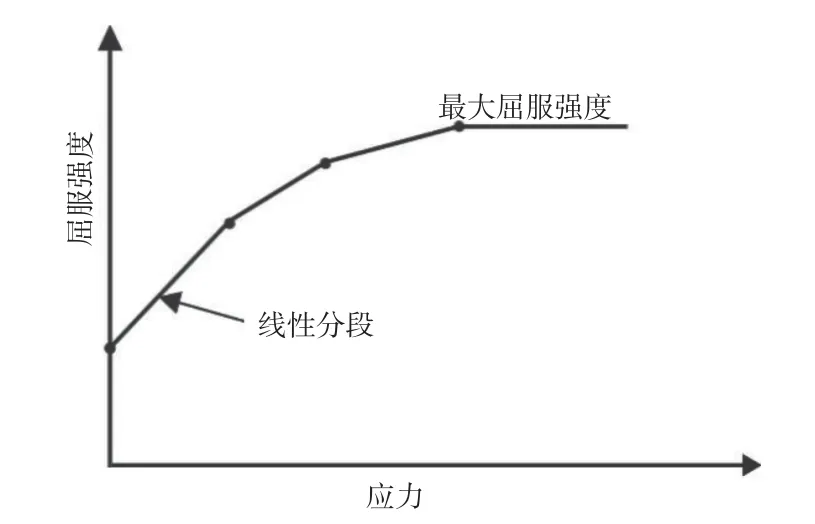
图1 D-P 分段曲线示意图Fig.1 Schematic diagram of D-P segmenting curve
在D-P 模型中,材料的屈服面在偏离平面上具有圆形横截面,可以表示为:
式中:λ和κ为材料常数;I1和J2分别为应力偏差张量的第一个和第二个不变量,定义如下:
式中:σ1,σ2,σ3为主要有效应力。
2 模拟结果与讨论
2.1 单一切削模拟
图2 和图3所示分别为方形和圆形磨粒在切削混凝土或钢筋的过程中,受到的应力变化和混凝土内部裂缝的变化情况。
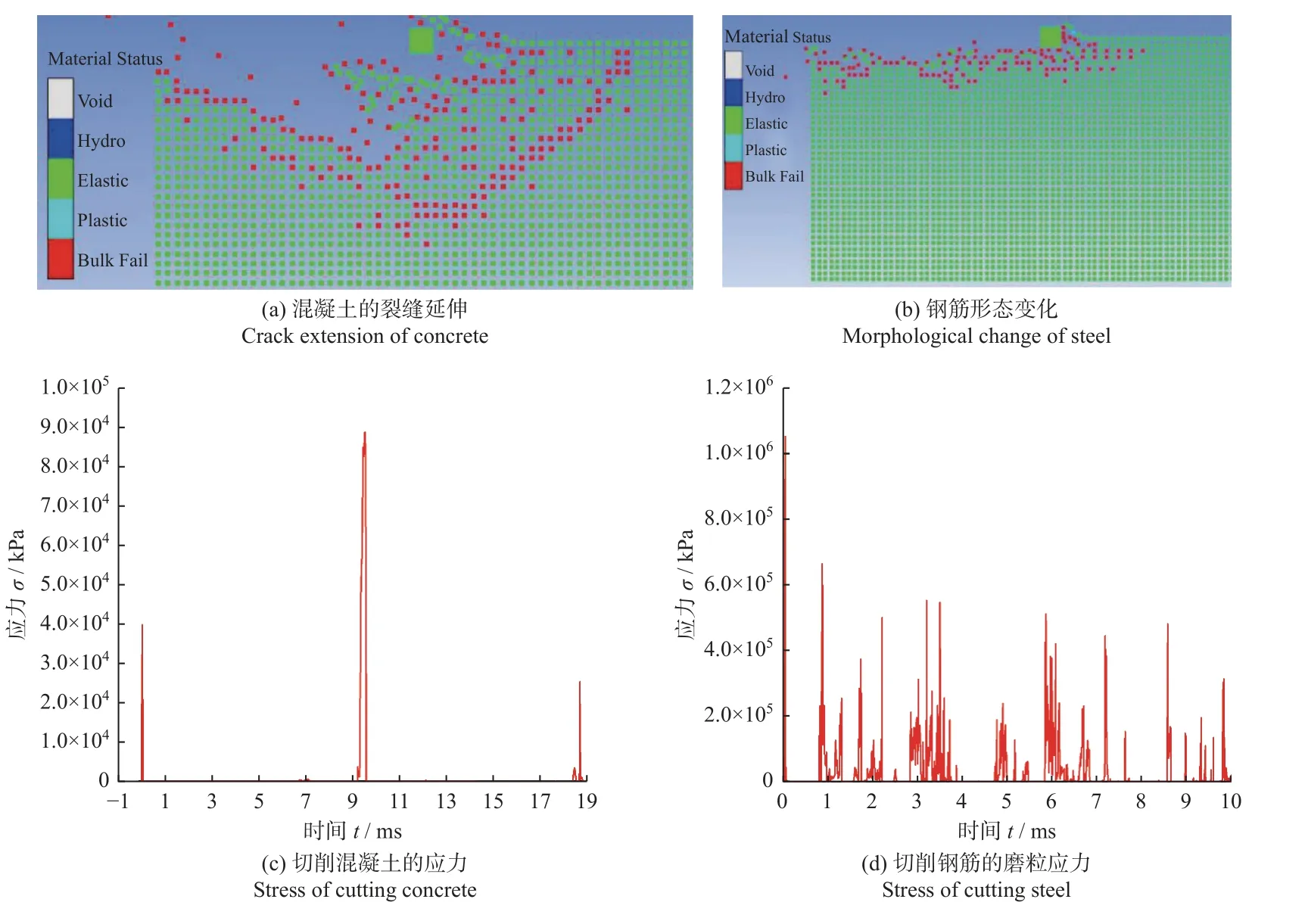
图2 方形磨粒切削混凝土和钢筋的变化Fig.2 Change diagrams of square abrasive particle cutting concrete and steel
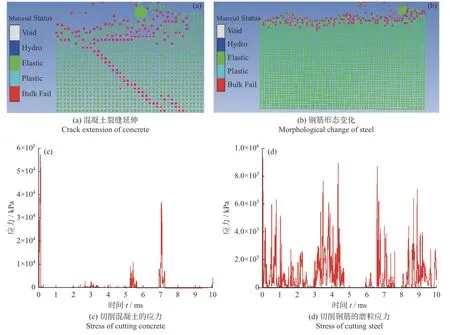
图3 圆形磨粒切削混凝土和钢筋的变化图Fig.3 Change diagrams of circular cutter cutting concrete and steel
图2a所示的混凝土切削过程中的形态变化和图2c所示的方形磨粒切削应力间断变化,表明方形磨粒对混凝土的切削是冲击性切削,混凝土在切削过程中会产生达到磨粒尺寸数十倍的碎屑和贯穿混凝土试样的延展裂缝。在切削过程中,混凝土的破碎分为3 个阶段:(1)磨粒撞击混凝土产生的应力沿其主应力方向延伸,产生主裂纹;(2)在主裂纹延伸的同时产生次生裂纹,其次生裂纹向混凝土试样表面延伸,并产生区域块状碎屑;(3)主裂纹与次生裂纹在磨粒前方产生相对于磨粒尺寸数十倍的破碎区,且该区域内的混凝土结构基本失效,导致磨粒在运动过程中会出现较大的受力真空区。此外,混凝土在切削过程中受到脆性破坏形成不平整切削面,导致实时切削有效面积发生变化,因而产生图2c 中所示的双倍应力峰值。
图2b 和图2d所示的钢筋材料基体形态变化和方形磨粒切削应力变化曲线表明,方形磨粒对钢筋的切削也是间断性的,但在初始切削时会因冲击作用产生显著大于稳定切削应力的峰值。同时,由于钢筋的塑性远大于混凝土,导致在钢筋材料中进行切削时不会产生贯穿裂缝,且形成的碎屑也远小于混凝土碎屑。
图3所示为圆形磨粒切削单一材料时的磨粒应力状态和被切削材料形态变化,其结果与方形磨粒切削时的变化基本一致。圆形磨粒形成的混凝土碎屑尺寸(图3a)明显小于图2a 中的碎屑尺寸(对应方形磨粒),导致圆形磨粒在相同的切削距离内会出现应力峰值数量(图3c)的增多,表明以面接触的方形磨粒相对于点接触的圆形磨粒存在更大的破坏影响区域。在钢筋的切削过程中,2 种磨粒产生的碎屑尺寸(图2b和图3b)大致相同,但圆形磨粒在初始撞击接触时产生的应力峰值(图3d)更低,而在稳定阶段的应力峰值没有明显区别。分析认为,这一现象可归因于2 种磨粒的切削破坏机理差异:方形磨粒在切削材料时主要以剪切破坏为主,而圆形磨粒在切削时同时包含挤压破坏和剪切破坏。圆形磨粒最前端对材料的破坏为剪切破坏;当圆形磨粒的最前端进入材料后,其最前端下方部分同样会以剪切破坏的形式进行,但由于最前端与磨粒下方部分存在高度差,导致磨粒最前端以下部分进行切削时需要对材料产生额外的挤压破坏才能保证碎块的正常形成。相比而言,方形磨粒的面剪切破坏不存在此现象,因此其切削应力峰值低于圆形磨粒条件。
2.2 钢筋混凝土组合切削模拟
图4所示为方形磨粒和圆形磨粒对钢筋混凝土组合进行切削时磨粒的应力变化和基体的形态变化。2种磨粒在切削时都会在产生较大的V 型剪切碎块(图4a 和图4b),并对混凝土块产生整体性的挤压破坏,但两者在碎块产生的临界位置、应力和形式上存在较大区别。钢筋的边界条件由单一材料切削模拟中的刚性边界条件变为具有可变性的混凝土边界,而材料的剪切强度均小于其屈服强度。因此,当磨粒的应力高于钢筋的剪切极限强度和混凝土的体积破坏屈服强度时,就会产生较大的V 型剪切碎片。
对于破坏范围较大的方形磨粒,与单一钢筋材料相比其切削应力峰值(图2c)会出现明显的升高现象(图4c),而圆形磨粒的切削应力(图4d)基本与单一钢筋材料时(图3d)保持一致。方形磨粒切削时产生的应力在初始阶段沿着水平方向,当延伸至临界位置(试样的水平和竖直非限制尺寸相同)后,应力会沿着剪切强度极限面传递。磨粒此时的应力为产生V型碎块的临界应力,且高于钢筋的剪切极限强度,但由于应力累积还未满足产生钢筋碎块的条件,因此切削时不会形成单一的钢筋碎屑而是形成整体的剪切破坏(图4a)。由于圆形磨粒前端的应力集中和破坏形式的限制,其无法在刚接触时产生对钢筋和混凝土整体破碎的应力值,使圆形磨粒形成V 型碎块的位置延后(图4b)。
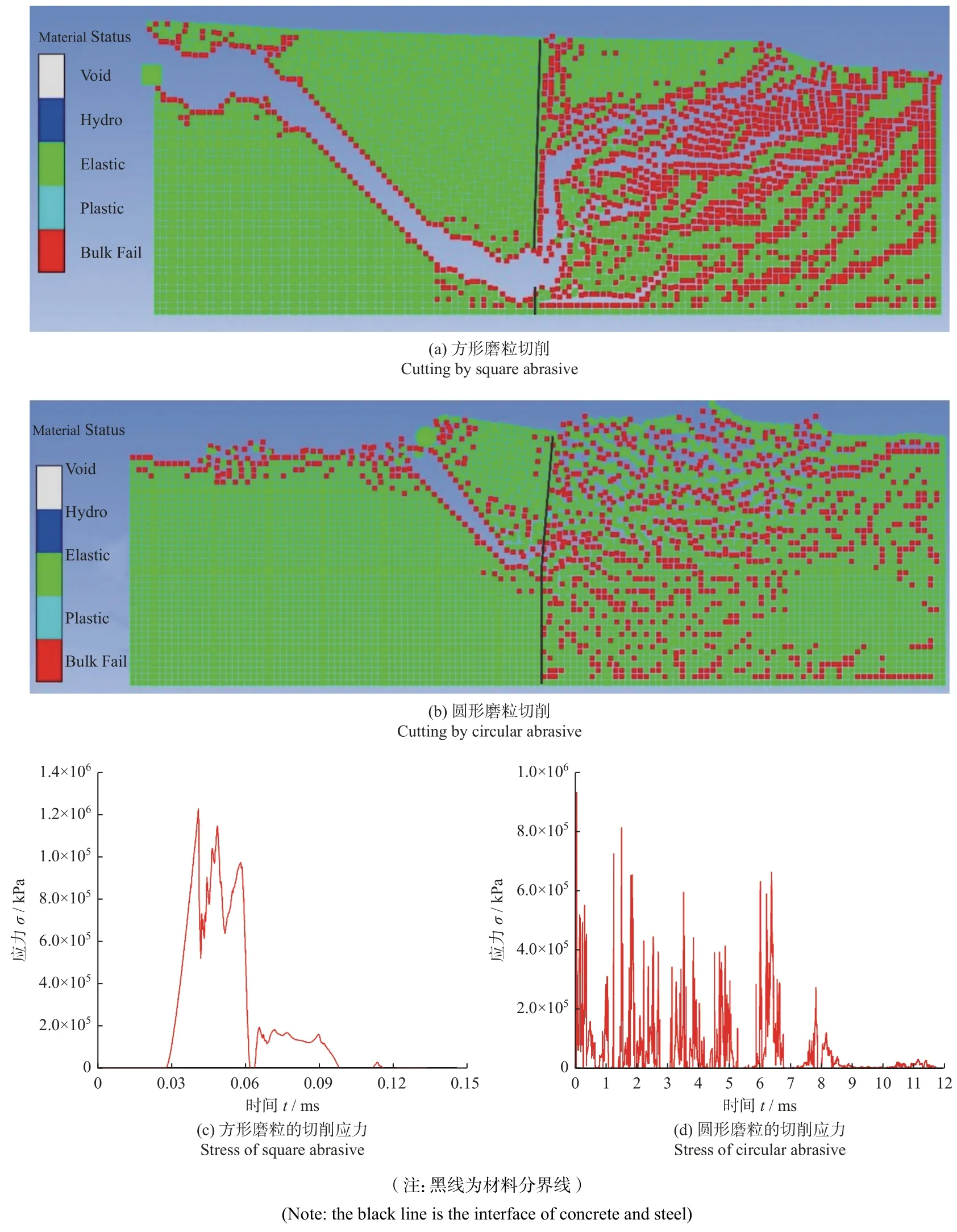
图4 磨粒切削钢筋混凝土组合的变化图Fig.4 Change diagrams of abrasive particle cutting reinforced concrete
2.3 混凝土钢筋组合切削模拟
图5 和图6所示为方形磨粒和圆形磨粒分别对混凝土钢筋组合进行切削时,磨粒的应力和基体的形态变化。方形磨粒和圆形磨粒进行切削时的应力变化曲线(图5b 和图6b)与磨粒在单一材料中的切削应力变化曲线(图2c、图2d、图3c 和图3d)基本保持一致。基体形态变化方面,无论是采用方形磨粒(图5a)还是圆形磨粒(图6a)进行切削过程模拟,都会在2 种材料的交界面处出现垂直的裂缝,促使2 种材料的分离。分析认为,该现象是2 种材料的塑性差异所致。钢筋被切削时会产生一定的塑性变形,且由于钢筋的塑性强于混凝土的塑性,钢筋产生的变形会对界面上的混凝土产生挤压破坏而形成垂直裂纹。
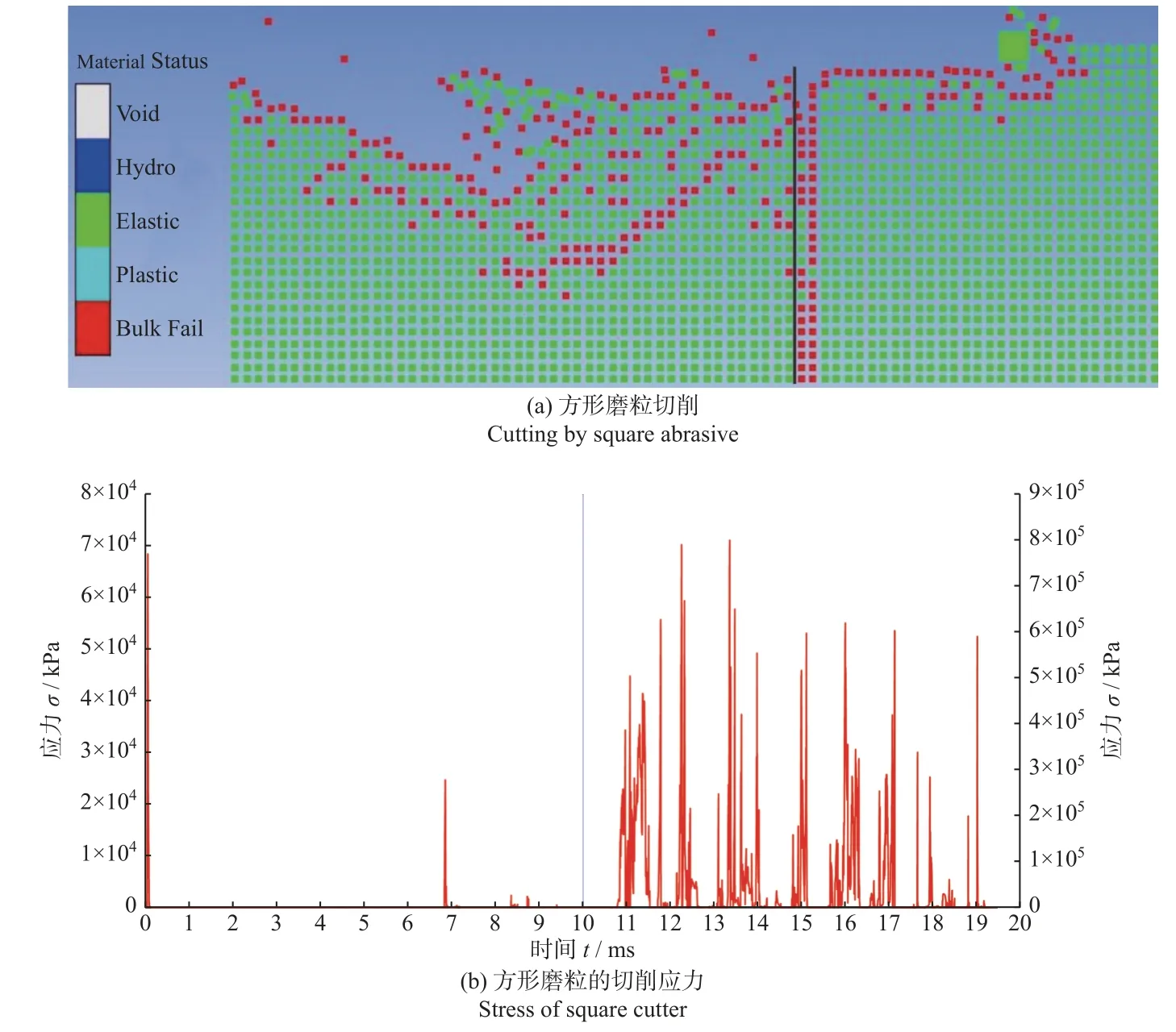
图5 方形磨粒切削混凝土钢筋组合形态变化与切削应力Fig.5 Change diagrams of suqare abrasive cutting reinforced concrete
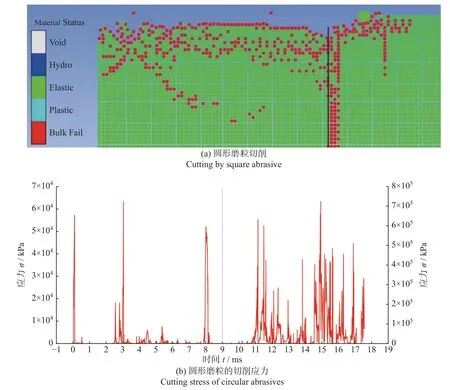
图6 圆形磨粒切削混凝土钢筋组合形态变化与切削应力Fig.6 Change diagrams of circular abrasive cutting reinforced concrete
对比可知,在所有模拟中,混凝土的破裂都是从切割边缘开始,并在磨粒前方延伸,进而形成主裂纹。主裂纹上衍生次生裂纹,并在靠近混凝土表面处延伸,形成碎屑。相比而言,圆形磨粒第二次接触基体材料后,会在磨粒后方一定范围内形成拉伸裂纹。由于磨粒和混凝土之间的弹性模量不匹配,加载时会在混凝土中形成应力集中区域,并在集中应力传播的路径上出现裂缝。当裂缝延伸贯通到表面时形成切屑,而磨粒前方也对应出现受力真空区。
方形磨粒主要的破坏形式为剪切和拉伸破坏,而圆形磨粒的破坏形式为剪切、拉伸和挤压破坏。钢筋为塑性材料,其切屑厚度与磨粒切深一致。切削过程中,切削应力沿切削方向不断发展,在累积损伤到达临界值后,形成断裂切屑。由于被切削对象的屈服强度存在差异,不论是由钢筋切向混凝土所形成的V 型碎块,还是由混凝土切向钢筋形成的结合面裂缝,都表明切削过程中的应力变化会降低材料之间结合面的强度,促使两者的分离。
方形磨粒相比于圆形磨粒,虽然在最开始阶段的撞击应力峰值高,但当其与试样稳定接触后,应力峰值低于圆形磨粒,形成的有效破碎面积也远高于圆形磨粒。总体而言,磨粒形状的差异本质是面切削和点切削的区别,两者在切削应力和有效破坏面积上都表明面切削可获得更好的切削效率,而点切削的平稳性更好。
3 结论
(1)SPH 方法在将材料密度引入本构方程、避免网格退化和畸变的情况下,能够准确有效地模拟切削过程中混凝土内部的裂纹变化以及当裂纹延伸到表面后形成碎屑并分离的行为。
(2)磨粒对混凝土和钢筋进行切削时,磨粒表面上的应力呈不连续分布,表明磨粒在切削过程中是以间断性冲击破坏基体材料。该破坏形式也表明在对非均质脆性材料进行切削磨粒设计时,不仅要考虑磨粒的硬度和耐磨性,也应使其具有一定的抗冲击韧性,防止磨粒被冲击破坏。
(3)切削模拟过程中混凝土与钢筋结合面之间的垂直裂缝表明,对不同脆塑性组合材料进行切削时会出现2 种情况:由高塑性的钢筋切向低塑性低强度的混凝土时会形成较大的剪切破坏,并对混凝土整体形成挤压破坏;由低塑性低强度的混凝土切向高塑性的钢筋时会首先对两者的结合面进行破坏,促使其分离。
(4)方形磨粒以面接触方式破坏基体相较于圆形磨粒的点接触破坏能在更短时间内对更大区域的钢筋混凝土进行破坏,从而获得更高的切削效率。同时,方形磨粒也会受到更大的初始切削应力,表明提高切削效率的同时也需要提高磨粒的自身强度。
