快堆堆芯单排组件抗震计算关键算法研究与验证

周世安,黑宝平,高付海

(中国原子能科学研究院,北京 102413)

对于反应堆及核设施,在强烈的外部载荷如地震作用下确保安全运行是最基本的要求之一。液态金属快堆(LMFR)中包含低压运行的系统以及薄壁柔性组件,这使其在地震作用下受到的影响极其显著。对于快堆堆芯,其地震下的运动主体十分庞大,全堆芯的六角形套管组件多达成百上千根,每根组件与相邻的6根组件均可能发生碰撞,且每时每刻的运动状态都在发生变化,从而导致碰撞的部位也随之变化,同时会受到液体金属冷却剂与组件流固耦合的影响,这使得堆芯抗震问题变得尤为复杂,因此建立针对快堆堆芯的抗震分析方法很有必要。

快堆堆芯的抗震分析方法通常分为设计试验和程序分析,试验数据直观可靠,但开展全堆芯组件抗震试验成本高昂,相比之下,研发专用程序以准确高效地进行全堆芯抗震计算和评价是一种经济可行的方式。国外许多国家已研发出了成熟的快堆堆芯抗震分析软件[1-5],有的软件是专用于堆芯抗震的计算程序,如日本研发的FINAS及REVIAN-3D、印度研发的CORE-SEIS、韩国研发的SAC-CORE和意大利研发的CORALIE及CLASH;有的则是在原有的通用成熟软件中进行了更新,使其具备快堆堆芯抗震计算能力,如法国的CASTEM,美国的COSMOS,俄罗斯的DINARA以及日本的FINDS、SAFA和SALCON。

程序设计采用的计算方法通常分为2种:模态叠加法和直接积分法。模态叠加法可提升计算速度,但忽略了高阶模态的影响;直接积分法则计算速度较慢。使用模态叠加法的程序有COSMOS、FINDS和SAFA等,SAFA还配置了专用于单自由度系统的Nigam时间积分法,更大程度地提高了计算效率。使用直接积分法的程序有CORE-SEIS、SACCORE、FINAS和SALCON等,SALCON在直接积分法的基础上采用GUYAN自由度凝聚方法减少矩阵维度,并通过变时间步长进一步提升计算效率。程序中堆芯组件管脚约束方式通常有3种:固支约束+等效弹簧、简支约束+间隙弹簧,以及固支约束+等效旋转弹簧元。大多数程序都可对管脚底端施加固支或简支约束,并在管脚球形密封处添加等效弹簧以施加间隙等效刚度,而FINDS与FINAS除对底端施加固支约束或简支约束外,还能使用旋转弹簧元来模拟管脚处的运动。碰撞动力方程的常用求解方法有中心差分法、Newmark法和基于Newmark法衍生的Wilson-θ法,其中Newmark法的参数γ和β变化时,算法的显隐式、计算速度和稳定性条件随之改变。本程序取γ=1/2、β=1/4,使Newmark法为平均加速度法,这种参数取法使算法为隐式且无条件稳定,通过这种取法保证求解的稳定性。冷却剂与堆芯组件的流固耦合计算方式有3种:集中附加质量法、均质化方法[6]和有限元计算法[5,7]。大部分程序常用集中附加质量法,该方法可调整组件的1阶固有频率以体现冷却剂对组件的附加作用。

中国原子能科学研究院曾使用ANSYS、FINAS以及CASTEM对快堆堆芯组件进行了初步的单根[8]以及单排组件抗震分析计算[9],但一直没有形成自主开发的堆芯抗震分析专用软件程序。

针对我国在快堆堆芯抗震计算自研专用程序方面的空白,本文研究建立适用于大规模快堆堆芯抗震分析的理论模型,研发能解决地震载荷作用下堆芯组件复杂非线性多点碰撞问题的时间历程关键算法,并从简单的悬臂梁振动理论解到国际原子能机构(IAEA)组织的法国RAPSODIE堆单排19根组件试验结果进行从下到上的逐步验证,完成单排组件情况下地震分析理论的建立与验证,证明算法的正确性和可行性,为后续多排组件乃至全堆芯抗震分析奠定基础。

1 理论模型

快堆堆芯组件在地震动时的动力学方程为:

(1)

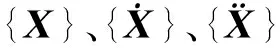
鉴于组件在地震过程中主要表现的行为是水平碰撞且在碰撞中基本没有轴向变形和剪切变形,故将组件简化为欧拉梁,并以此为根据构建初始的质量矩阵与刚度矩阵。

1.1 质量矩阵和刚度矩阵

仅考虑两端受载的情况,则欧拉梁的梁平衡方程为:

(2)

其中:u为梁的挠度,即梁单元节点处垂直于轴线方向的位移;E为梁的弹性模量;I为梁的惯性矩。

通过Hermite插值方程表示的梁形函数与虚位移原理,可推导出梁的单元刚度矩阵和单元质量矩阵,通过对不同参数梁的单元矩阵进行装配最终获得总的质量矩阵和刚度矩阵。为保证计算精度足够高并大幅提升计算效率,本文采用GUYAN缩减法[10]进行相应的自由度缩减。首先需要选定主从自由度,其中主自由度是施加了力、计算边界条件和需要输出结果的所在自由度,其余的则是从自由度。本质上,缩减矩阵是使用主自由度来表示从自由度。对于包含阻尼和外力作用的系统,其动力学方程为:

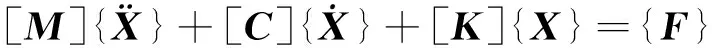
(3)

其中,{F}为受到的外力向量。

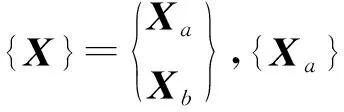
(4)

根据静平衡近似,可得到:

(5)

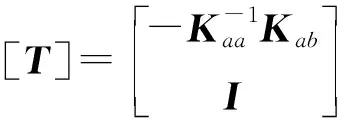
[K][T]{Xb}={F}

(6)

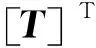
(7)

(8)

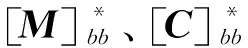
1.2 结构阻尼矩阵

对于地震作用下的堆芯组件,除流固耦合产生的附加阻尼及碰撞时产生的碰撞阻尼,组件结构本身存在结构阻尼,工程上常用Rayleigh阻尼[11]来表示。Rayleigh阻尼可表示为:

[C]=a0[M]+a1[K]

(9)

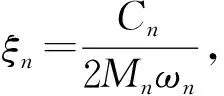
(10)

对于新型结构,通常情况下需通过试验测量获取各阶精确阻尼比和频率。快堆堆芯组件材料一般为不锈钢,但燃料组件和屏蔽组件内部结构材料和工艺设计有所差异,因此二者阻尼比不同。由于快堆堆芯组件为细长梁结构,第1阶和第2阶振型对相邻组件的碰撞行为起主要作用,故在求解堆芯抗震总动力方程的结构阻尼矩阵时,分别选取对应上述振型的第1阶和第2阶固有频率和阻尼比。在确定ω1和ω2及ξ1和ξ2的基础上,若ξ1=ξ2=ξ,则a0和a1可表示为:

(11)

1.3 碰撞刚度及阻尼

通常情况下,快堆堆芯组件的碰撞刚度可通过以下两种方法获取:1) 直接法,通过对真实组件进行碰撞试验直接获取程序所需碰撞刚度;2) 间接法,通过组件壁面的挤压刚度间接计算求得程序所需碰撞刚度。本文采用间接法计算碰撞刚度Kgap,可通过式(12)求得[1]。

(12)

其中,Ket1和Ket2分别为发生碰撞的两根组件的挤压刚度。

挤压刚度可通过对组件施加如图1所示的压力使其发生形变来求得。通过有限元对组件进行建模,两端施加力F,计算出ΔD,便可求出组件的挤压刚度Ket:

(13)

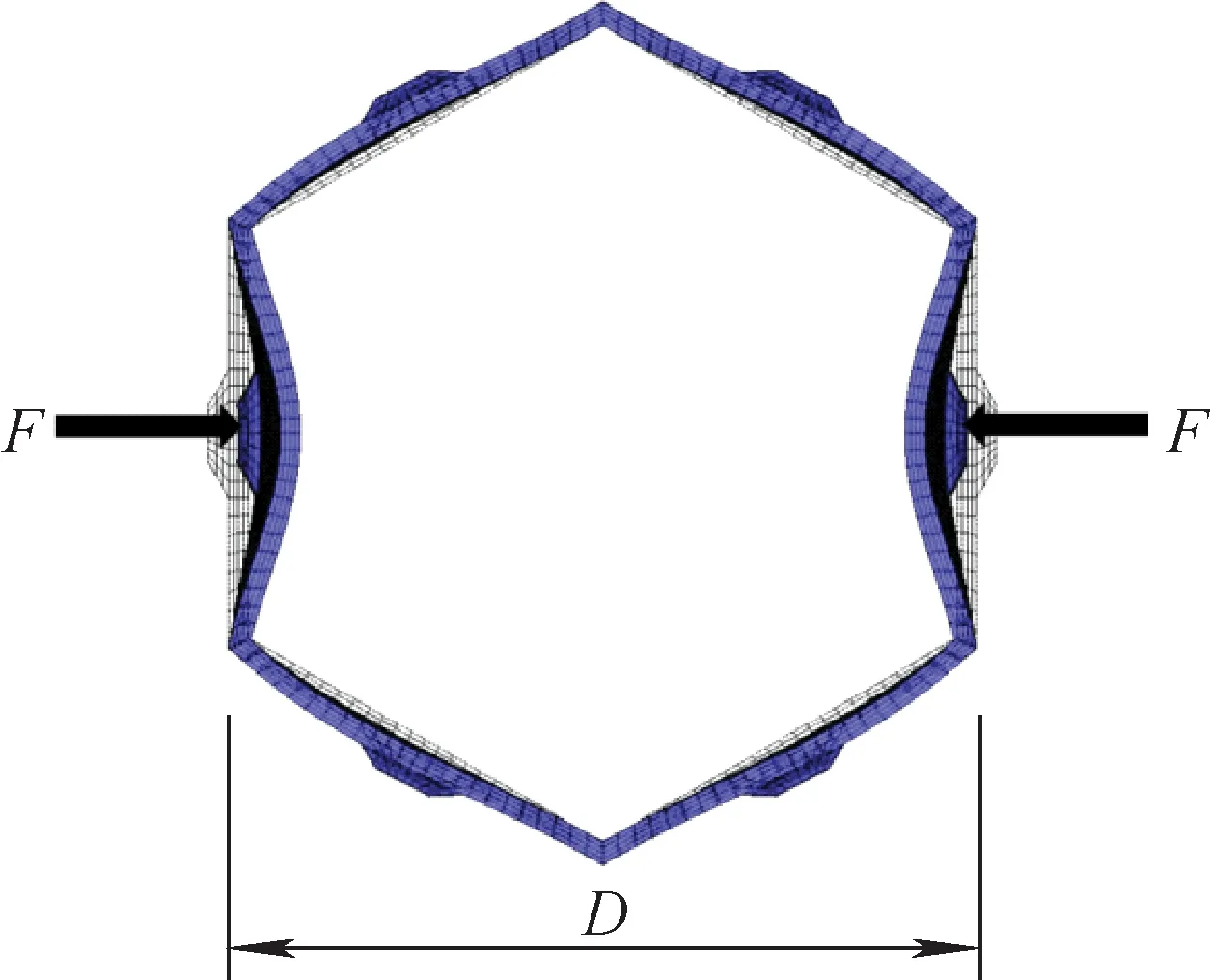
图1 挤压刚度计算示意图Fig.1 Schematic diagram of extrusion stiffness calculation

当发生碰撞的两根组件的结构材料和截面形状一致时,Ket1=Ket2=Ket。根据碰撞刚度Kgap计算得到冲击阻尼Cgap:

(14)

其中,e为材料的弹性系数,对于不锈钢,e一般为0.55。

在单排组件的情况下,组件垫块处节点的位移无需根据几何位置关系进行分解,此时刚度的设置得到相应的简化。当第j根组件受到前后两根组件的冲击时,总刚度矩阵和阻尼矩阵变为如下形式:

(15)

aj-1=cj-1+Pgap

(16)

bj-1=-Pgap

(17)

其中:c为原始总刚度矩阵和阻尼矩阵在碰撞组件处的对应项;Pgap为碰撞产生的冲击刚度或冲击阻尼;a为碰撞对刚度矩阵和阻尼矩阵在对角项上产生的影响;b为碰撞对刚度矩阵和阻尼矩阵在非对角项上产生的影响。

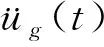
2 基准例题验证

2.1 等截面悬臂梁固有频率验证

对于简单的等截面悬臂梁(图2),其存在固有频率理论解。将梁截面参数输入到研发的自研程序内,计算固有频率并与理论解进行对比,以验证梁单元的构建与装配,以及自由度缩减法则的正确性。

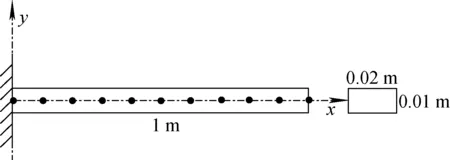
图2 简单等截面悬臂梁示意图Fig.2 Simple uniform cantilever beam

图2所示等截面矩形梁,长为0.02 m、宽为0.01 m、高为1 m。其杨氏模量为2.1×105MPa、密度为7.85×103kg/m3、泊松比为0.3。将该梁分别在ANSYS与自研程序中建模并与理论解进行对比,结果列于表1。对比发现:自研程序计算的前3阶固有频率与理论解和ANSYS的计算结果完全吻合,随着阶数的升高,误差逐渐变大,在前5阶,频率相对误差均小于1%。

2.2 中国实验快堆堆芯燃料组件固有频率验证

真实组件管脚和栅板插座为间隙配合装配。对中国实验快堆(CEFR)堆芯燃料组件进行质量等效与刚度等效,等效参数列于表2。

表1 简单等截面悬臂梁固有频率计算结果对比Table 1 Comparison between theoretical and calculation results of nature frequency in simple uniform cantilever beam example

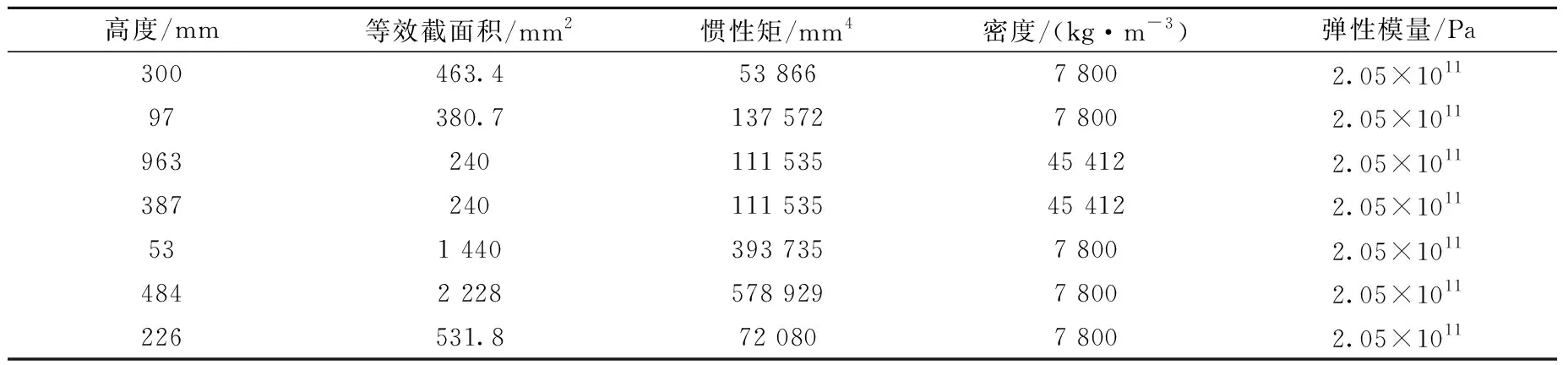
表2 CEFR堆芯燃料组件等效后的梁参数Table 2 CEFR core fuel assembly equivalent beam parameter

组件可等效为变截面梁,在管脚底端设置为简支约束,且在管脚球形密封处设置刚度为8.8×105N·m的等效弹簧[12],将模型参数输入自研程序和ANSYS中计算固有频率并进行对比,结果列于表3。从表3可知,二者吻合较好,最大误差在第3阶处,仅为0.49%。2.1和2.2节中梁的约束条件不同、截面参数不同,因此梁单元的构建和矩阵自由度缩减方式均不同,通过这两个案例可验证组件等效方法的合理性,同时也可验证程序梁单元构建以及GUYAN缩减法的正确性。

表3 CEFR堆芯燃料组件ANSYS与自研程序固有频率计算结果对比Table 3 Comparison between nature frequenciesin CEFR core fuel assembly by ANSYS and code

2.3 CEFR单根组件空气中时程分析验证

在堆芯组件大规模非线性碰撞情况下,ANSYS计算精度低且计算时间长,但单根组件不存在碰撞时其计算结果是具有可信度的。通过单根组件在自研程序和ANSYS中计算结果的对比,可验证时程分析法的正确性。

图3 KOBE波地震输入Fig.3 Kobe earthquake seismic input

针对2.2节中提到的CEFR燃料组件模型,采用ANSYS和自研程序分别进行时程分析计算,其中KOBE波地震输入如图3所示,计算结果对比如图4所示。由图4可知,二者基本吻合,其中ANSYS计算的组件顶点处位移最大值为5.263×10-4m,自研程序计算的组件顶点处位移最大值为5.320×10-4m,二者相对误差为1.08%,由此证明单组件的时程分析法是正确的。

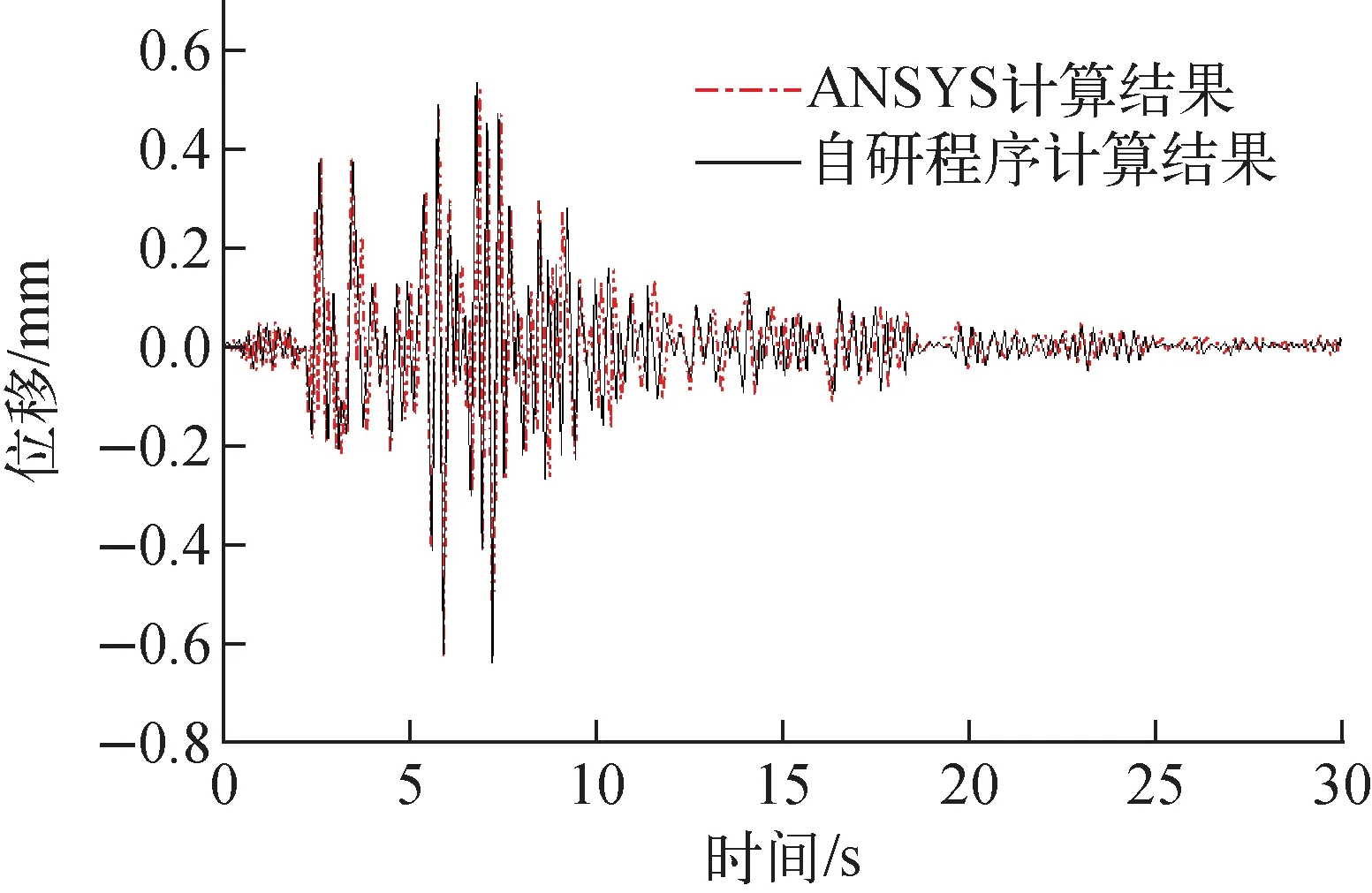
图4 ANSYS与自研程序对CEFR单组件时程分析结果对比Fig.4 Comparison between time historical calculation results calculated by ANSYS and code

2.4 RAPSODIE堆单排19组件空气中时程分析验证

IAEA于1987年到1995年以法国、日本和意大利快堆堆芯抗震试验为基准组织并开展了各成员国快堆堆芯抗震程序对比验证的大型会议活动,试验的组织情况列于表4。

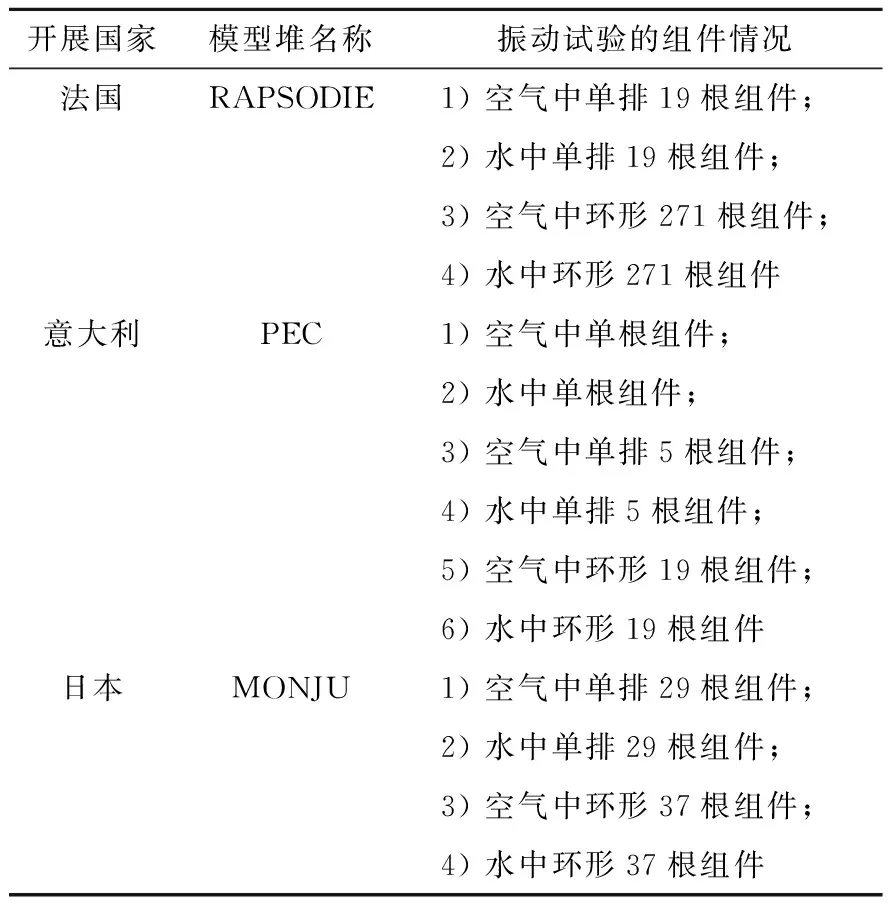
表4 IAEA试验组织情况Table 4 Model reactor and seismic testconducted by IAEA

为验证相邻组件碰撞时碰撞刚度和阻尼设置的正确性,采用表4中法国RAPSODIE堆空气中单排19根组件碰撞试验数据对自研程序进行验证。该试验包含燃料组件(F/A)和屏蔽组件(N/S),排列方式如图5所示。组件上下两个碰撞垫块分别位于1.28 m和0.71 m处,燃料组件的1阶、2阶阻尼比为3%,屏蔽组件的1阶、2阶阻尼比为1%,梁截面参数与试验测得的碰撞刚度和碰撞阻尼参考日本FINDS程序的设置[2]。

在自研程序中,燃料组件与屏蔽组件底端均设置为固定约束,而燃料组件在管脚球形密封处设置一个刚度为6×106N/m的弹簧以等效间隙带来的影响,计算固有频率并与试验结果对比,如表5所列。可发现,第1阶固有频率程序计算结果和试验结果符合良好。试验未给出第2阶和第3阶固有频率。

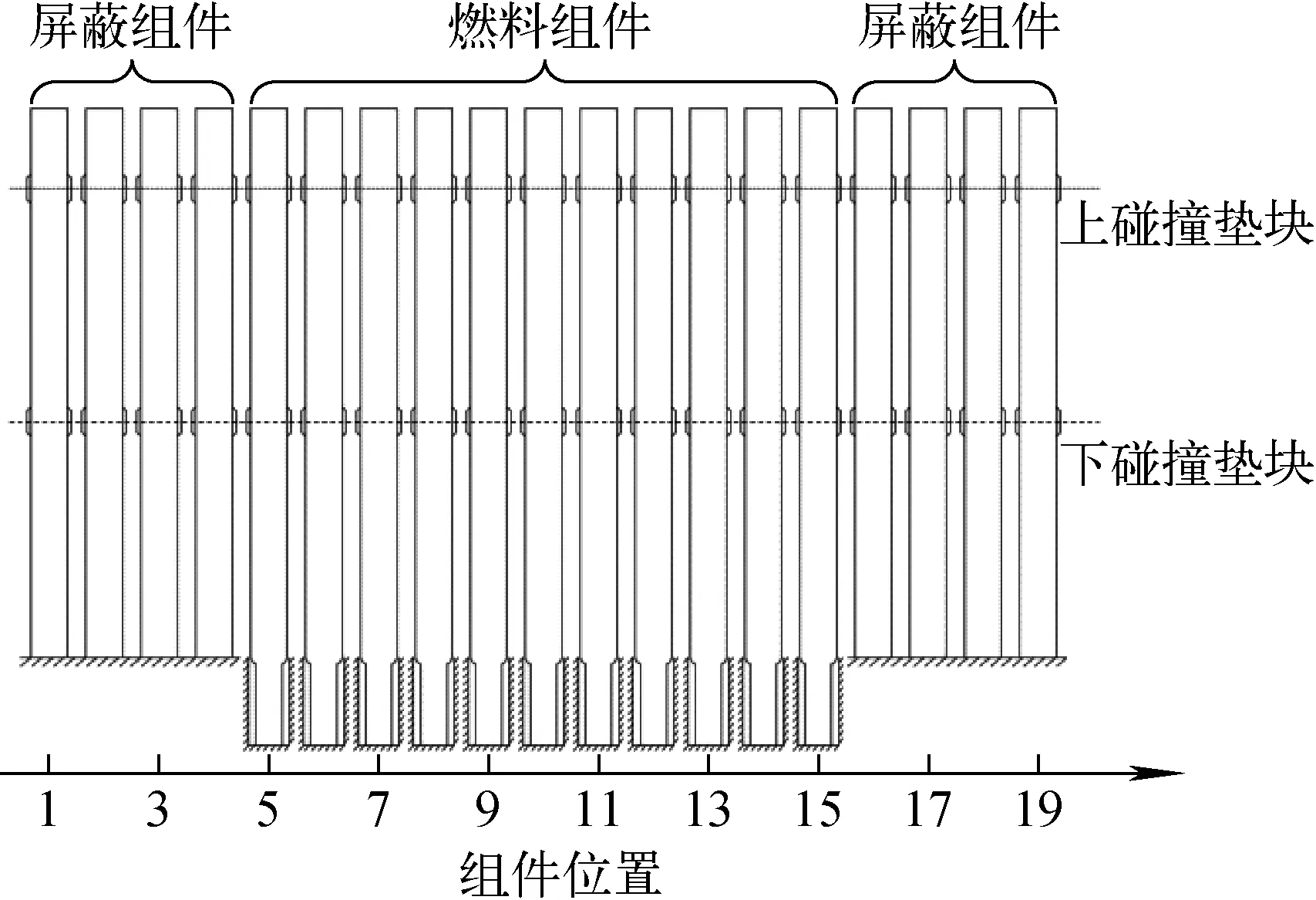
图5 RAPSODIE单排试验排列简图Fig.5 Layout of RAPSODIE reactor in single row assemblies test

表5 程序计算和试验所测固有频率对比Table 5 Comparison between natural frequency results calculated by code and measured from test

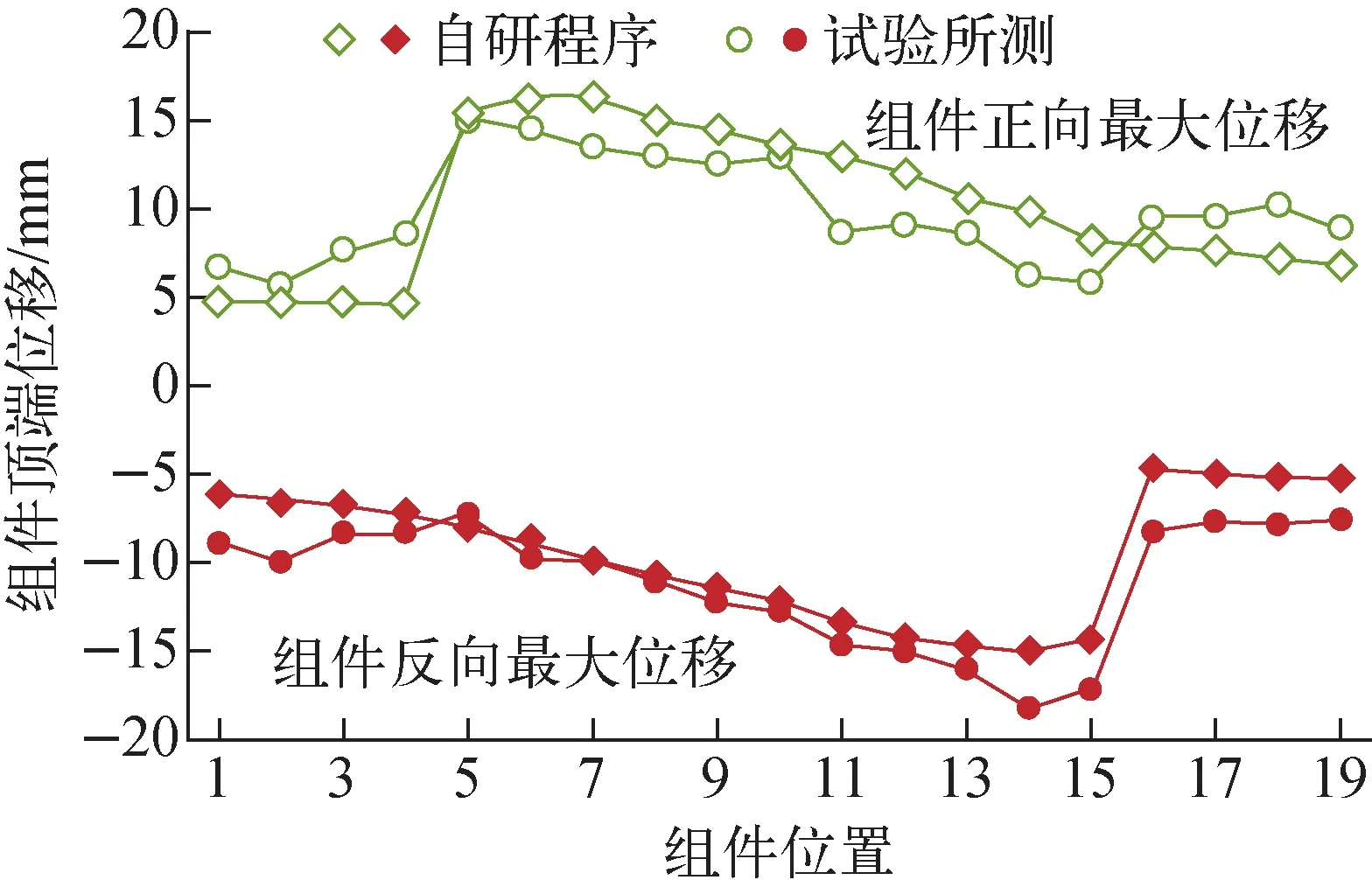
图6 程序计算和试验所测组件最大位移对比Fig.6 Comparison between max assembly displacement calculated by code and measured from test

将水平地震波RAP087[2]输入自研程序,在考虑组件间碰撞的情况下进行时程计算,提取每根组件顶部的最大位移并和试验所测结果作对比,如图6所示。可看出二者计算结果接近,其中燃料组件的最大位移基本吻合,误差主要出现在屏蔽组件上,但堆芯抗震更加关注燃料组件的冲击与变形,因此证明程序时程分析法的计算结果是可靠的。

3 结论

本文在国内外快堆抗震程序开发和试验验证调研的基础上,建立了快堆堆芯抗震理论模型,阐述了堆芯组件等效简化以及碰撞刚度和阻尼处理方法,解决了堆芯组件多点复杂非线性碰撞的关键性问题,选择适用于快堆堆芯组件在地震载荷作用下的隐式Newmark法进行了时程分析计算,提出了快堆单排组件抗震分析理论算法,并将该理论算法进行代码开发。通过从简单悬臂梁到复杂变截面简支梁的固有频率计算,以及单组件和单排多组件的时程分析计算,从下而上逐步验证了本文所建立的抗震模型和算法的正确性。后续将进一步考虑液体对组件运动的流固耦合影响并将二维算法扩展到三维,拓展程序适用范围的同时提高计算精度。