含绕丝棒束低流速时阻力特性的实验研究
2023-05-18周志伟李虹锐薛秀丽曾泽华
周志伟,李虹锐,薛秀丽,曾泽华,刘 瑞,刘 健,罗 锐
(1.中国原子能科学研究院 核工程设计研究所,北京 102413;2.清华大学 能源与动力工程系,北京 100084;3.华北电力大学 动力工程系,河北 保定 071003)
钠冷快堆作为第4代反应堆中技术较为成熟、发展前景较好的快中子堆[1],在极大提高核资源利用率的同时还能够嬗变长衰变期的次锕系核素,降低核废料处理的成本和对环境的威胁,是我国热中子堆-快中子堆-聚变堆三步走核电发展战略的重要环节[2]。如何保证反应堆堆芯的绝对安全是核电技术发展的关键问题,反应堆的非能动安全技术也因此成为各国研究人员关注的热点[3-6]。钠冷快堆的非能动事故余热排出系统,利用堆芯钠流的自然循环,将反应堆紧急停堆后堆芯产生的衰变余热排出,防止堆芯组件超温熔毁,保证了极端事故工况下堆芯的安全。
非能动事故余热排出工况时,钠冷快堆堆芯钠流在自然循环驱动下从栅板联箱进入堆芯组件,将堆芯组件燃料棒的衰变余热带出到热钠池,这个过程中通过堆芯组件钠流的流量决定了钠流对组件燃料棒的冷却功率,而钠流流量的大小则由钠流自然循环时因温度场形成的驱动力和钠流受到的阻力相平衡确定。钠冷快堆事故紧急停堆时,钠流流量减小为额定流量的1%~3%,此时堆芯组件对钠流的摩擦阻力占钠流自然循环所受总阻力的90%以上[7]。因此,研究确定堆芯组件在小流量低流速时的摩擦阻力特性对于钠冷快堆非能动事故余热排出系统的设计和优化具有重要意义。
钠冷快堆的堆芯组件一般设计为绕丝棒束结构[8],由绕丝缠绕的燃料棒正三角排列成正六边形的棒束,绕丝棒束装入正六边形的套管,形成堆芯组件。作为钠冷快堆堆芯热工水力设计的重要参数之一,很多学者对绕丝棒束组件的摩擦阻力进行了实验研究,并给出了一系列的经验关系式[9]。但现有的绕丝棒束组件摩擦阻力实验研究多是对组件在高流速时摩擦阻力的研究,测量了组件内流体流动处于转换区和湍流区的摩擦阻力系数,而对组件在低流速时摩擦阻力的实验研究很少[9-15]。自1967年Rehme第1次测量绕丝棒束组件的摩擦阻力以来,各国研究人员对共计162个绕丝棒束组件的摩擦阻力进行了实验测量,其中仅有35个组件的摩擦阻力实验测量了组件在层流区的摩擦阻力系数,占被测量组件总数的21.6%[16]。同时,上述35个测量了组件层流区摩擦阻力的实验研究,其研究重点也在高流速区域,每个实验层流区的工况点仅有几个,组件层流区摩擦阻力系数的总数据点个数在所有组件摩擦阻力系数数据点个数中的占比小于10%[17]。绕丝棒束组件低流速时摩擦阻力实验数据太少的现状,严重制约了现有绕丝棒束组件摩擦阻力系数经验公式在低流速时的预测精度。因此,更多更详细的绕丝棒束组件低流速时摩擦阻力实验数据,被认为是进一步提升绕丝棒束组件摩擦阻力系数经验公式计算性能的关键[17-18]。
为了测量得到组件在低流速时的摩擦阻力特性,本文搭建有机玻璃材质(PMMA)的37棒绕丝棒束组件摩擦阻力测量实验台,以改进液柱测压方法,准确测量组件在绝热工况Re=200~1 100时的摩擦阻力系数,并与现有绕丝棒束组件摩擦阻力系数经验公式(这些公式计算的也是组件绝热工况时的摩擦阻力系数)的预测结果进行对比。
1 实验系统和数据处理
1.1 摩擦阻力测量实验台
绕丝棒束组件摩擦阻力测量实验台如图1所示,主要包括待测量的37棒绕丝棒束组件、稳压水箱、调节阀、热电阻、测压管面板和称重计量容器等。在绝热流动稳定工况下,组件内流体的流动满足雷诺相似,因此使用去离子水作为测量介质,实验结果整理成雷诺数Re和摩擦阻力系数的形式,这样,测量结果可以根据雷诺相似准则很方便地应用在钠流流体,具体的推导证明过程请参考文献[19]。待测量的37棒绕丝棒束组件使用有机玻璃材质制造,图1展示了组件的结构示意及其几何参数。范大军[19]的实验结果以及Raj等[20]和Chen等[21]的数值模拟结果都证实了绕丝棒束组件内流体的流动具有以绕丝螺距H为周期的周期性,组件不同壁面测量得到的流体在整数倍H轴向距离的摩擦阻力压降相同。因此,待测量组件设置了6个测压截面,相邻测压截面轴向间隔H或7H,每个测压截面在组件入口管所在壁面正对的壁面上布置1个取压孔,即以组件绕丝的起点为起始点,沿组件轴向方向,在组件0.25H、1.25H、2.25H、3.25H、4.25H、11.25H处设置取压孔,共布置6个取压孔。
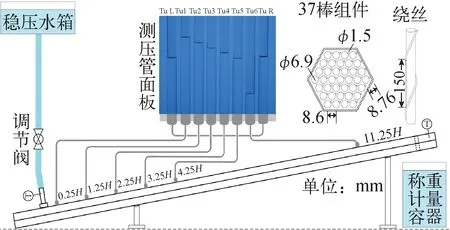
图1 绕丝棒束组件摩擦阻力测量实验台结构示意图Fig.1 Schematic diagram of friction pressure drop measurement loop for wire-wrapped rod bundle assembly
测量组件低流速摩擦阻力时,流过组件水流的体积流量很小,使用体积流量计测量水流的流量误差较大。此外,组件内流体低流速流动时,流体受到的摩擦阻力压降很小,大概只有百帕的量级,已经属于微压测量范围,使用压差变送器测量如此小的摩擦阻力压降,同样会有很大的误差。测量组件低流速摩擦阻力时对流量测量和压差测量的高精度要求,可能是现有组件摩擦阻力实验研究在低流速时实验数据较少、实验数据不确定度较大的主要原因之一。本文为了提高流量测量的精度,未采用体积流量计测量,而是测量了流过组件水流的质量流量,然后使用水流温度对应的水流密度换算得到体积流量;为了提高压差测量的精度,将数字图像技术引入液柱式压力计,使得液柱式压力计0~300 Pa测量范围的测量绝对误差从25 Pa[22]减小到2 Pa以内。同时,实验使用稳压水箱代替水泵给绕丝棒束组件供水,极大减小了摩擦阻力测量时水流流动的不稳定波动。
测压管面板使用匀光板,面板表面固定有机玻璃管作为测压管。引压管为硅胶材质软管,一端连接待测量组件的取压孔,一端连接测压管。取压孔处压力通过引压管传导至测压管,在测压管内形成液柱。为了更准确地确定液柱之间的高度差,使用高分辨率相机对测压管拍照,读取液柱图像中液面的像素坐标,通过像素长度和实际长度的比值进行换算,确定液柱的高度和液柱液面投影的几何形状。0~300 Pa测压范围时,使用液柱图像定位液柱高度和液柱液面投影形状的定位精度约为0.04 mm,相对于肉眼定位液柱高度时约1 mm的定位精度有大幅的提高。在测压管面板左右侧各固定1个测压管Tu L和Tu R,两个测压管底部相连接使Tu L和Tu R测压管内的液柱是完全水平状态,以此来修正测压管面板照片未完全水平、测压管安装未完全竖直等带来的系统误差。得到液柱液面投影的几何形状后,通过液柱液面的形状计算液柱液面产生的表面张力,对液柱液面在空气中的表面张力进行修正,进一步提高压差测量的精度。使用静态测量和等精度测量实验验证了本文使用的压力测量方法和体积流量测量方法的误差,测量结果显示,在0~300 Pa压力范围内,压差测量的相对误差小于1.05%,在300~1 500 Pa压力范围内,压差测量的相对误差小于0.5%;在0~0.4 m3/s范围内,体积流量测量的相对误差小于0.2%,在0.4~2.0 m3/s范围内,体积流量测量的相对误差小于0.6%。
1.2 实验数据处理
实验测量得到通过组件的体积流量qv(m3/s)和各测压管液柱修正后的高度H1~H6(m),则各测压管对应的取压孔之间的摩擦阻力压降由式(1)计算:
Δpij=ρg(Hi-Hj)
(1)
式中:ρ为水流温度对应的水流密度,kg/m3;g为重力加速度,取9.8 m/s2;i、j为测压管对应取压孔的标号;Δpij为两个取压孔之间组件的摩擦阻力压降,Pa。计算得到摩擦阻力压降后,由式(2)计算对应的摩擦阻力系数:
(2)
式中:fij为两个取压孔之间组件的摩擦阻力系数;l为两个取压孔之间的距离,m;De为组件的等效水力直径,De=0.004 055 m;v为组件内水流的流速,m/s,由式qv/s计算,s为组件内的流通面积,s=0.001 189 m2。体积流量qv对应的水流Re由下式计算:
Re=vDe/ϑ
(3)
式中,ϑ为水流温度对应的水的运动黏度,m/s2。
实验时,流过组件前后的水流温度恒定,整个实验过程中因稳压水箱供水泵和水流流动造成的水流温度缓慢升高幅度在0.5 ℃以内,可以忽略温度测量误差、水流密度和运动黏度的误差。组件的几何误差也很小,同样可以忽略。根据误差传播定律,测量得到的组件摩擦阻力系数和Re的标准差可以由式(4)、(5)计算[14]:
(4)
(5)
式中:σf为摩擦阻力系数的标准差;σRe为Re的标准差;σΔpij为摩擦阻力压降的标准差,Pa;σqv为体积流量的标准差,m3/s。本文取2倍标准差作为测量结果的不确定度。
为了将实验测量得到的摩擦阻力系数和现有绕丝棒束组件摩擦阻力系数经验公式的预测值作比较,本文选取了能计算组件在层流区和转换区摩擦阻力系数的BDD公式、MBDD公式、KIR公式、CTS公式和UCTD公式,使用这些公式计算了待测量组件的摩擦阻力系数以进行比较。上述公式的具体计算方法参见文献[9]和[23]。
2 实验结果与讨论
2.1 入口段对棒束摩擦阻力的影响
流体进入绕丝棒束组件后,需要流经一定长度才能成为流动比较稳定的充分发展流动状态,这部分棒束即流体进入组件后的入口段。在组件的入口段,由于流体从入口管进入绕丝棒束流道时流道面积和流动方向的急剧改变,对流体流动形成了剧烈的扰动,表现为流体在入口段流过1个绕丝螺距产生的摩擦阻力压降与流体在充分发展段流过1个绕丝螺距产生的摩擦阻力压降并不相同,即所谓的入口段效应[15]。为了研究入口段对组件摩擦阻力的影响,分别测量了组件在0.25H~1.25H(10De~50De)、1.25H~2.25H(50De~90De)、2.25H~3.25H(90De~130De)位置的摩擦阻力系数,并和组件在4.25H~11.25H(167De~441De,充分发展段)的摩擦阻力系数进行了对比,测量结果如图2所示。
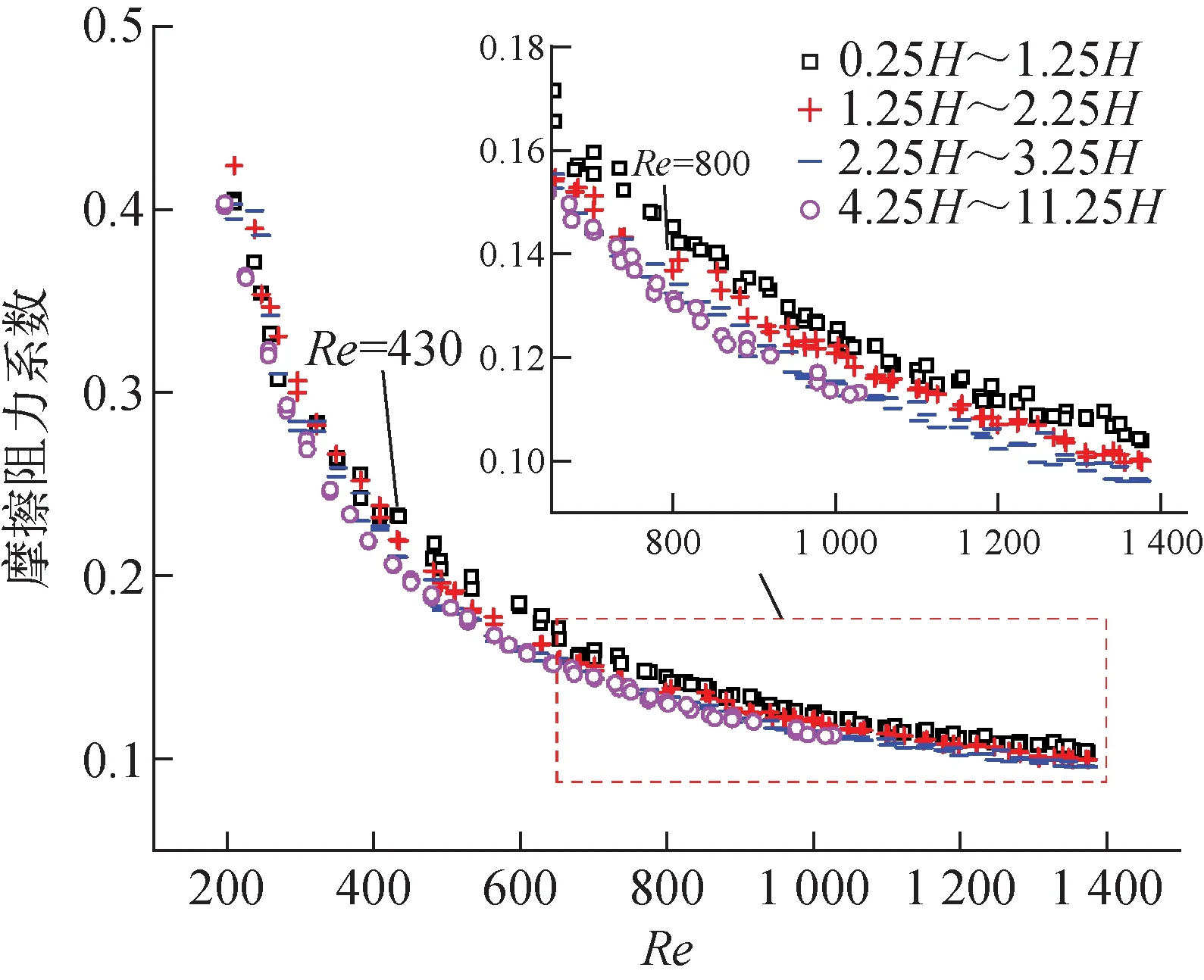
图2 绕丝棒束组件不同绕丝螺距位置的摩擦阻力系数Fig.2 Friction factors of wire-wrapped bundle assembly at different winding pitches of wire
从图2可看到,在整个测量Re范围内,组件2.25H~3.25H和4.25H~11.25H的摩擦阻力系数保持一致,但是0.25H~1.25H和1.25H~2.25H的摩擦阻力系数在不同Re范围内表现出了差异。在Re小于430时,组件不同绕丝螺距的摩擦阻力系数基本一致,Re大于430后,0.25H~1.25H的摩擦阻力系数相较其他绕丝螺距开始偏大,当Re进一步增加,大于800后,1.25H~2.25H的摩擦阻力系数也开始偏大,而在Re大于1 300后,1.25H~2.25H的摩擦阻力系数和2.25H~3.25H的摩擦阻力系数有再度吻合的趋势。图2的测量结果表明,Re较小时,流体的流速低,组件的入口段较短,小于10De,此时10De后的棒束均位于充分发展段,因此不同H的摩擦阻力系数基本保持一致。随着Re的增加,流体的流速增加,组件的入口段长度逐渐增加,在Re大于430时,入口段长度开始大于10De,此时0.25H~1.25H的棒束开始包含部分入口段,摩擦阻力系数相较处于充分发展段的棒束的摩擦阻力系数偏大。同理,在Re大于800时,入口段长度开始大于50De,此时1.25H~2.25H的棒束也开始包含部分入口段,进而摩擦阻力系数增加。在Re大于1 300时,1.25H~2.25H和2.25H~3.25H的摩擦阻力系数出现再度吻合的趋势,可能是因为流体流动中湍流流动增加所致。随着流体流速的增加,流体逐渐从层流开始向湍流过度,流体首先在绕丝棒束流道狭窄处最先产生湍流,流速进一步增加时,产生湍流流动的流体区域随之增加,即产生湍流流动的区域在整个流动区域的占比不断增加[24],而湍流流动需要的入口段长度相比层流流动缩短很多[25],因此随着湍流流动区域占比的增加,减小了入口段长度。综上所述,绕丝棒束组件在低流速时,其入口段长度随着流速的增加而增大,随着流动开始向湍流转变而减小。本文测量的37棒PMMA绕丝棒束组件的入口段长度小于90De。
2.2 棒束的摩擦阻力系数
图3示出了水流流过位于充分发展段的4.25H~11.25H范围棒束组件的摩擦阻力压降,红色误差棒表示测量结果的不确定度。从图3可看出,绕丝棒束的摩擦阻力在特别小流速时(v<0.103 m/s),随着流速的增加线性增加,呈现出层流流动时摩擦阻力和流速关系的特性。随着流速的增加,棒束的摩擦阻力和流速偏离线性关系,摩擦阻力开始随着流速的1.29次方增加,表明组件内流体内部出现了湍流,流体开始从层流流动向湍流流动转变。当流速进一步增加时,流体流动中湍流流动的占比逐步变大,组件的摩擦阻力开始随着流速的1.46次方增加。上述测量结果表明,绕丝棒束组件内部流道几何结构虽然十分狭小复杂,但是在低流速时,组件内流体流动依然表现出和圆管等简单几何结构内部流体流动相一致的摩擦阻力特性。同时,测量结果能捕捉到随流速的增加,组件摩擦阻力压降和流速关系中流速的指数不断增大这一现象,表明测量结果具有足够的精度。

图3 绕丝棒束组件的摩擦阻力压降Fig.3 Friction pressure drop of wire-wrapped bundle assembly
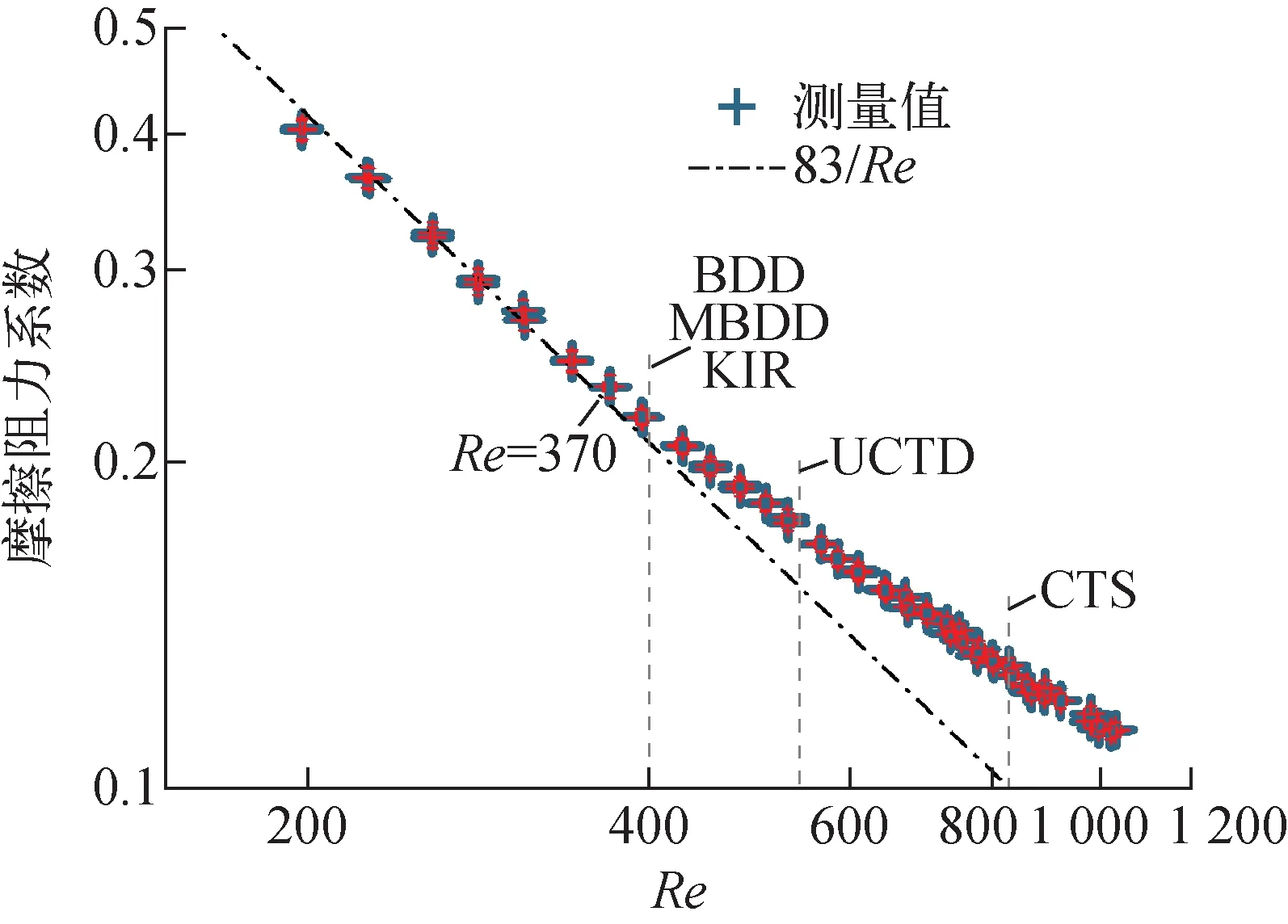
图4 绕丝棒束组件的摩擦阻力系数Fig.4 Friction factor of wire-wrapped bundle assembly
将测量得到的摩擦阻力压降整理成摩擦阻力系数和Re的关系,如图4所示。Re<370时,组件的摩擦阻力系数和Re呈反比关系,随着Re的增加快速下降,组件内流体为层流流动,组件的层流常数(即组件Re和摩擦阻力系数的乘积)为83。Re>370时,组件的摩擦阻力系数开始偏离反比关系,随着Re增加而下降的速度减缓,组件内流体开始从层流向湍流转变[16]。因此,组件从层流向湍流转捩的临界Relt约为370。图中还标注了使用现有绕丝棒束组件摩擦阻力系数经验关系式计算的Relt。BDD、MBDD、KIR 3个经验公式认为组件的Relt与组件几何结构无关,是值为400的常数。CTS和UCTD公式认为组件的Relt是组件P/D的函数,针对本文测量的组件,CTS公式计算的Relt=828,UCTD公式计算的Relt=560。现有公式中,BDD、MBDD、KIR公式对本文测量的37棒组件的Relt计算较准确,而UCTD公式和CTS公式高估了本文测量组件的Relt,CTS公式高估的更多。实际上,UCTD公式正是发现了CT公式(CTS公式是CT公式中的1个)高估了组件的Relt,从而导致其计算组件从层流向湍流转变时的摩擦阻力系数的性能不佳,因此对CT公式进行了更新而得到。但从测量结果来看,虽然UCTD公式减小了Relt,但针对本文测量的组件,UCTD公式对Relt的计算还是存在一定幅度的高估。
2.3 实验值和经验公式计算值的比较
将测量得到的绕丝棒束组件摩擦阻力系数和现有的绕丝棒束组件摩擦阻力系数经验公式的计算值进行了对比,如图5所示。在组件内流体层流流动时(Re<370),5个用来对比的经验公式计算得到组件摩擦阻力系数都比测量得到的实验值偏高,其中BDD、MBDD、KIR公式偏高较多,UCTD和CTS公式偏高较少,偏高了约7%。在流体流动进入层流向湍流的转换区时,UCTD公式的计算值和实验值吻合得很好,BDD、MBDD、KIR公式的计算值相对于实验值依然偏高,而CTS公式因为高估了组件的Relt,导致其在流体流动刚进入转换区时计算值偏低。比较UCTD公式和CTS公式计算值和实验值的一致程度,可发现UCTD在减小Relt后,对流体流动从层流进入到转换区时组件的摩擦阻力预测精度有了很大提高。同时,虽然UCTD公式高估了组件的Relt,但由于其在层流区优异的预测精度,使得其相较BDD、MBDD、KIR 3个公式(这3个公式对Relt预测更准确),对组件在低流速时的摩擦阻力预测精度更高。现有经验公式的计算值较实验值高,除了经验公式的计算误差外,可能也受测量的绕丝棒束组件为PMMA材质的影响,因为相较于不锈钢材质的组件,PMMA材质的表面粗糙度较小。考虑这一因素,UCTD公式在计算真实绕丝棒束组件低流速摩擦阻力系数时,误差会更小。
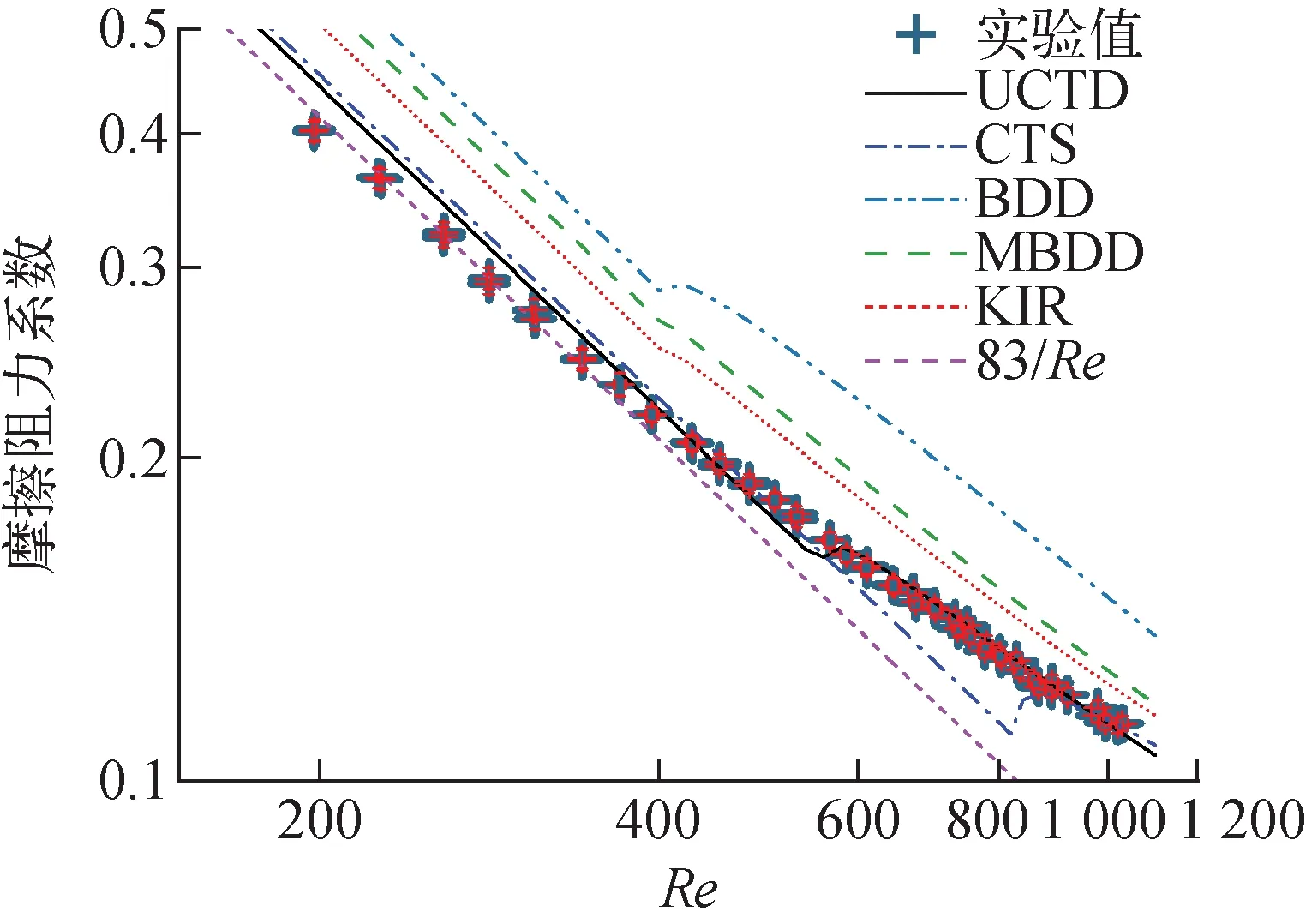
图5 绕丝棒束组件摩擦阻力系数实验值和经验公式计算值的对比Fig.5 Comparison between measured and computed friction factors of wire-wrapped bundle assembly
3 结论
本文准确测量了PMMA材质的37棒绕丝棒束组件在Re=200~1 100时的摩擦阻力系数,并和现有绕丝棒束摩擦阻力系数经验公式的预测结果进行了对比,主要结论如下。
1) 绕丝棒束组件在低流速时,其入口段长度随着流速的增加而增大,随着流动开始向湍流转变而减小。
2) 本文测量组件的Relt=370,现有经验公式中,BDD、MBDD、KIR公式对Relt计算较准确,而UCTD公式和CTS公式高估了该值。
3) 现有的经验公式在计算组件低流速摩擦阻力系数时,UCTD公式的计算值和本文测量组件的实验值最吻合。在流体层流流动时,UCTD公式高估了约7%;在流体进入层流向湍流的转换区时,UCTD公式的计算值和实验值基本一致。
