静默式热管反应堆热工水力特性不确定性分析

韩睿钰,王成龙,郭凯伦,苏光辉,秋穗正,田文喜

(西安交通大学 核科学与技术学院,陕西 西安 710049)

反应堆数值计算能为反应堆的设计及其安全分析提供必须的数据,然而,假设条件、计算模型及方法的不确定性会导致计算结果存在一定的不确定性[1]。完善不确定性分析对反应堆设计分析及其安全评审具有重要意义[2]。

为促进核能系统不确定性分析研究,经济合作与发展组织核能机构(OECD-NEA)成立了专家组以进行不确定性分析建模[3],分别针对轻水堆[4]、高温气冷堆[5]和钠冷快堆[6]进行了不确定性分析研究。Wang等[7]利用DAKOTA耦合RELAP5对棱柱式熔盐冷却高温堆稳态热工水力特性进行了不确定性分析;兰兵等[1]利用DAKOTA耦合外部程序开展了AP1000堆芯关键参数的不确定性分析;王可等[8]针对CPR1000开展了关键参数对事故结果影响的不确定性分析;岳倪娜等[9]基于自主开发的THACS程序,根据国际原子能机构提供的EBR-Ⅱ事故SHRT-17试验数据,对钠冷快堆进行了不确定性分析。

热管反应堆是一种新型核反应堆系统,其利用热管非能动地把堆芯产生的热量导出,具有固有安全性好、结构简单、模块化等优势,在空天、海洋等领域具有广阔的应用前景[10]。

目前,针对热管反应堆的分析主要集中在多物理场耦合方面。Tang等[11]研究了热管反应堆在不同运行条件下的热电耦合特性;Ma等[12]建立了兆瓦级热管反应堆的核-热-力耦合模型;Guo等[13]考虑热管反应堆的中子输运、热传导和热膨胀3个典型物理过程,进行了稳态耦合计算。针对热管反应堆暂无不确定性分析相关研究,有必要尽快开展相关研究为热管反应堆后续研究提供参考,从而促进热管反应堆发展。

本研究以静默式热管反应堆NUSTER单通道为对象,采用基于拉丁超立方方法的开源不确定性分析程序DAKOTA[14]以及热管反应堆单通道热工计算程序HEART,使用统计抽样法进行不确定性分析。

1 抽样方法及系统概述

1.1 拉丁超立方抽样方法

蒙特卡罗抽样和拉丁超立方抽样(LHS)是两种常见的不确定性统计抽样分析方法。当抽样规模较大时,蒙特卡罗抽样方法会出现大量重复抽样值(或近似抽样值),为解决这个问题,McKay等[15]提出了LHS方法,显著提高了抽样效率。

LHS方法规定在每个固定区间仅随机抽取1个样本点。假设对N维对象进行K次抽样,定义P=(pjk)为一个N×K维矩阵,用于储存抽样中间过程的数据,Q=(qjk)为一个N×K维矩阵,用于储存最终抽样结果。则LHS过程[16]如下:将每一维均分为K个区间,然后可重复在每个区间随机抽取N个值,对于第k个子区间,随机抽取后可得到1个集合(p1k,p2k,…,pNk),即为矩阵A的第k列。打乱A中每行的顺序得到的矩阵B表示随机抽样得到的K个样本点,其每列向量即为1个样本点。

1.2 系统概述

本文以静默式热管反应堆NUSTER为研究对象,其固有安全性好、智能与自主控制水平较高、系统简单、能在无换料情况下低噪声工作5年以上,可满足海洋重型UUV的动力需求[7]。

图1为NUSTER堆芯总体设计图,堆芯共有480根燃料棒,燃料芯块分别采用富集度为73%、55%和19.75%的二氧化铀,燃料包壳材料采用钼,上下反射层材料为氧化铍。热管工质选择液态碱金属钾,吸液芯及管壁材料均选用316不锈钢。堆芯可分为109个通道,单个通道的结构设计图如图2所示。具体热工及物理设计参见文献[17-19]。

图1 NUSTER堆芯设计图Fig.1 Design for NUSTER

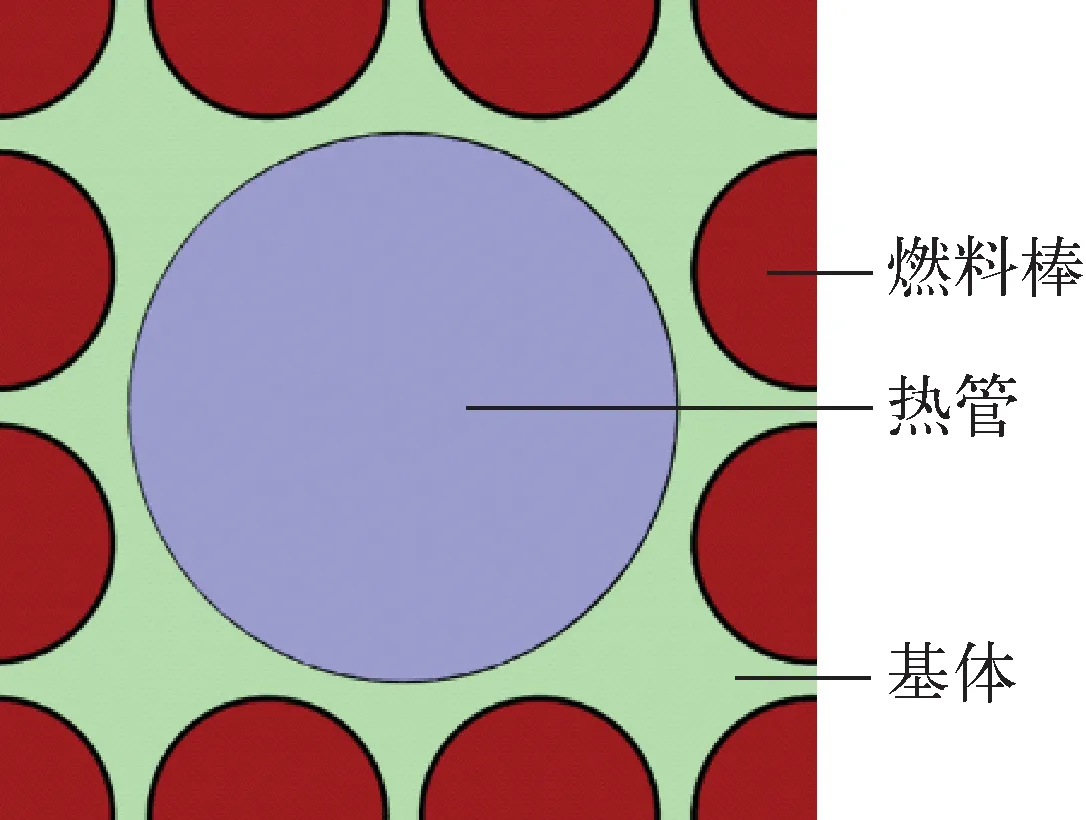
图2 NUSTER单通道设计图Fig.2 Design for single channel of NUSTER

2 不确定分析方法

2.1 分析方法

采用统计抽样法分析静默式热管反应堆的不确定性,统计燃料峰值温度、包壳峰值温度、基体温度、热管蒸发段温度及热管冷凝段温度的分布,分析计算反应堆失效的概率。热管反应堆的不确定性分析流程图如图3所示,具体方法步骤如下:1) 依据现有的热管反应堆设计参数、相关实验数据及分析程序等,确定输入参数的统计特征;2) 利用DAKOTA程序采用LHS方法生成N组输入样本;3) 利用生成的N组输入样本生成HEART程序输入卡片并计算;4) 统计目标参数分布,对输入参数进行不确定性分析。

样本总数的选取与不确定性结果分析中统计时所需的容许概率和置信水平有关,本文采用Wilks关系式[20]确定样本总数:

1-an≥b

(1)

(1-an)-n(1-a)an-1≥b

(2)

式中:n为样本数;a×100%为容许概率;b×100%为置信水平。其中,式(1)适用于单侧容许区间,式(2)适用于双侧容许区间。本文取样遵循95%的容许概率、95%的置信水平原则,根据式(2)可知,选取样本不得少于59组。在保证取样合理的前提下,尽可能节省计算资源,本文共选取样本150组。

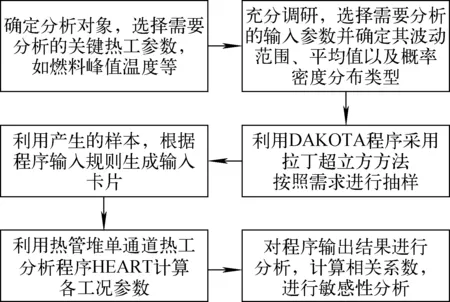
图3 热管反应堆不确定性分析流程图Fig.3 Calculation flowchart for uncertainty analysis of heat pipe cooled reactor

2.2 输入参数选取

采用燃料峰值温度、包壳峰值温度、基体温度、热管蒸发段温度和热管冷凝段温度作为目标参数,为保证热管反应堆安全运行,目标参数温度应低于稳态工况下相应的温度限值。在热管反应堆运行过程中,影响目标参数的因素很多,本文不能一一考虑。目前,热管反应堆大多为概念堆,缺少相关的运行数据,本文在选择输入参数时,主要参考了新型海洋静默式热管反应堆(NUSTER-100)电源系统概念设计[17-19]和美国洛斯阿拉莫斯国家实验室的热管电源系统(HPS)[21]以及在此基础上进行的SAFE-30实验[22]的相关实验数据与计算结果。热管反应堆中的热管以纯导热方式工作,其工作特性与功率有直接关系,此外,还需考虑对导热系数影响较大的重要位置的几何参数。初步分析各因素的重要性后,本文选取可能对目标参数影响最显著的6个输入参数进行分析。各输入参数的概率密度分布采用正态分布,波动范围采用3σ(3倍标准方差)假设,6个输入参数的统计特性列于表1,其中括号内数据为各变量对应的变异系数。

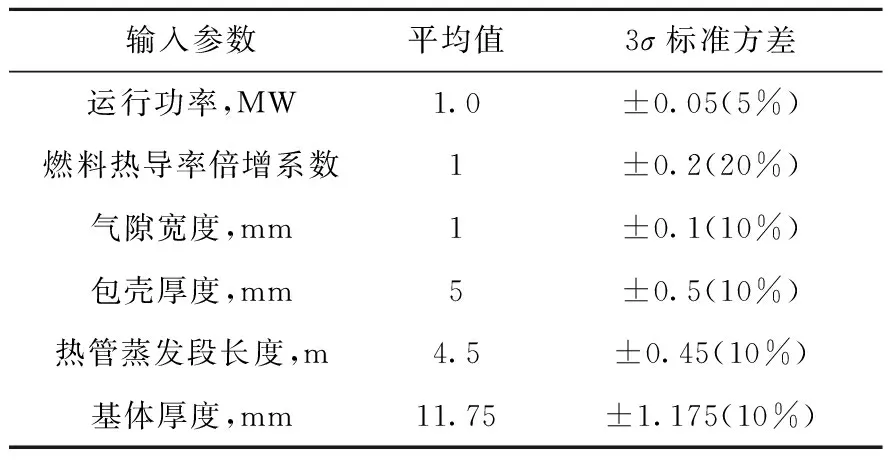
表1 输入参数的统计特性Table 1 Statistical characteristics of input parameter

图4为各输入参数的概率密度分布。可发现,运行功率分布最集中,而燃料热导率分布较均匀。图5为利用DAKOTA程序采用LHS方法抽取的运行功率样本散点图,可见大部分抽样点在±3σ范围内。

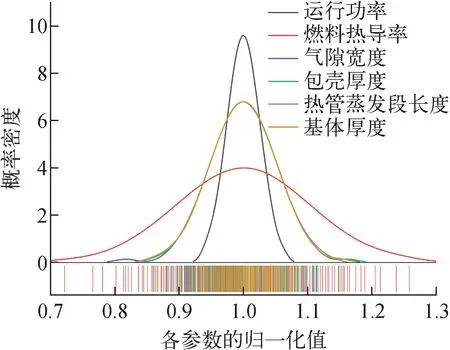
图4 输入参数的概率密度分布Fig.4 Probability density distribution of input parameter

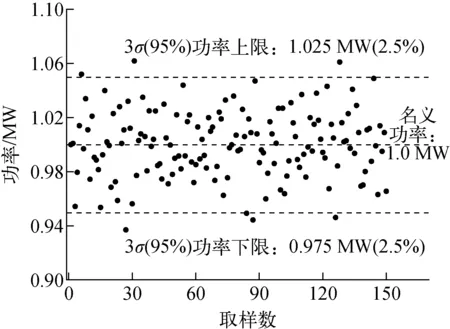
图5 运行功率样本Fig.5 Power sample

3 结果分析

利用HEART程序对热管反应堆单通道稳态情况进行了计算,燃料峰值温度、包壳峰值温度、基体温度、热管蒸发段温度和热管冷凝段温度分别为1 469.38、1 258.35、1 241.61、1 206.51、1 149.31 K。其中,燃料峰值温度限值为3 100.15 K,包壳峰值温度与基体温度限值为2 890.15 K,热管蒸发段与冷凝段温度限值为1 473.15 K,各目标参数的温度均小于相应的温度限值。

3.1 DAKOTA抽样模型验证

采用抽样模拟方法分析不确定性结果是否可信很大程度上取决于随机样本的生成效果,本文选取3组符合正态分布的数组A、B、C对DAKOTA程序抽样结果进行验证,3个数组的期望和标准差列于表2,选取验证模型D=A2+2B-C,将DAKOTA的抽样结果与解析解进行对比,结果列于表3。可发现,当抽样次数为103时,抽样结果期望及标准差与解析解的相对误差分别为0.571%和0.447%,二者非常接近。因此,可认为DAKOTA的抽样结果具有可信度。

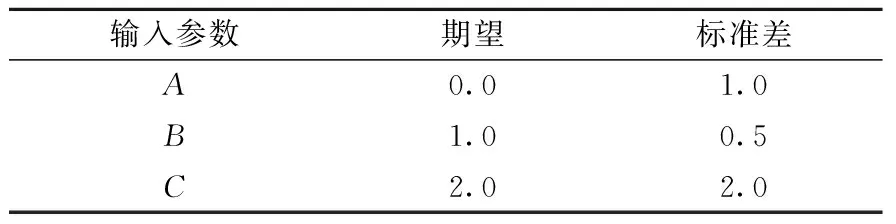
表2 用于验证DAKOTA程序的输入参数Table 2 Input parameter for verifing DAKOTA

表3 解析解与程序抽样结果对比Table 3 Comparison of analytical result with sampling result

3.2 HEART程序验证

HEART[23]是一个热管反应堆单通道热工分析自编程程序,采用Fortran编译。为确保其计算结果的有效性,分别对其关于堆芯及热管的计算结果进行验证。图6、7分别为堆芯轴向及径向功率分布的验证结果,可发现程序计算值与设计值吻合良好。将热管壁面温度的计算结果与实验数据进行对比,如图8所示,二者吻合良好。因此,可认为HEART程序关于热管反应堆堆芯及其中热管的计算结果是有效的。

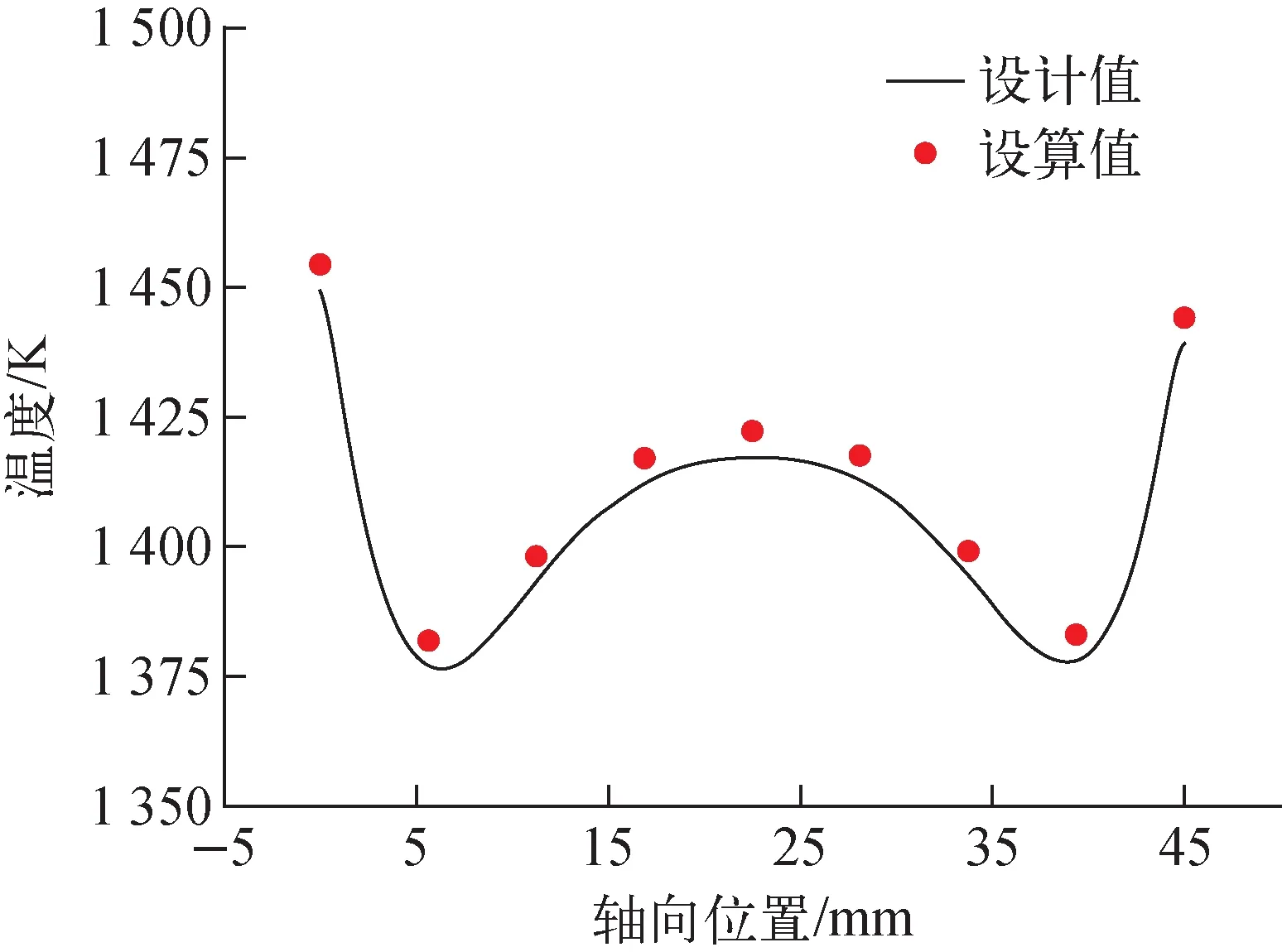
图6 轴向功率分布验证Fig.6 Verification of axial power distribution

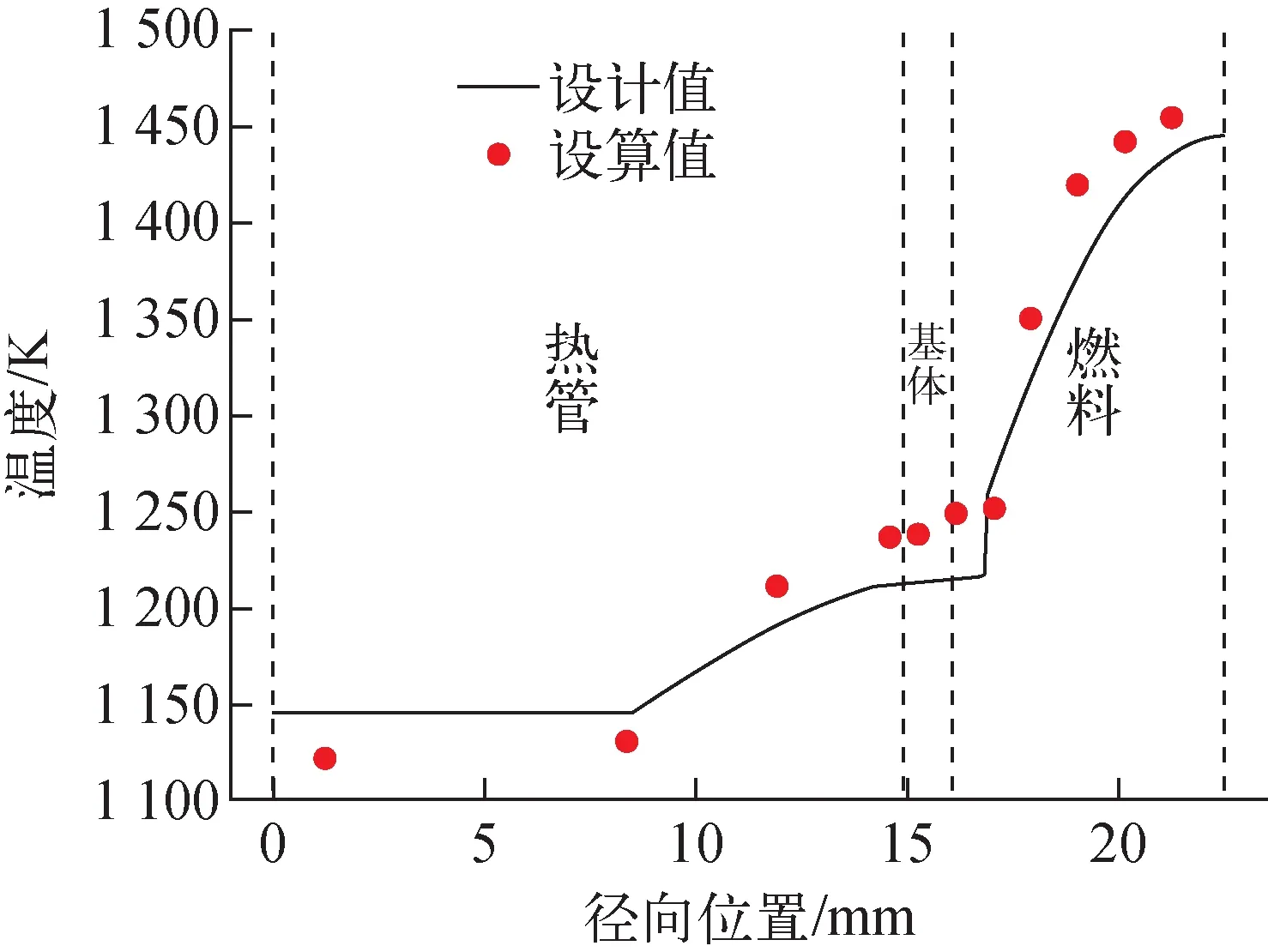
图7 径向功率分布验证Fig.7 Verification of radial power distribution

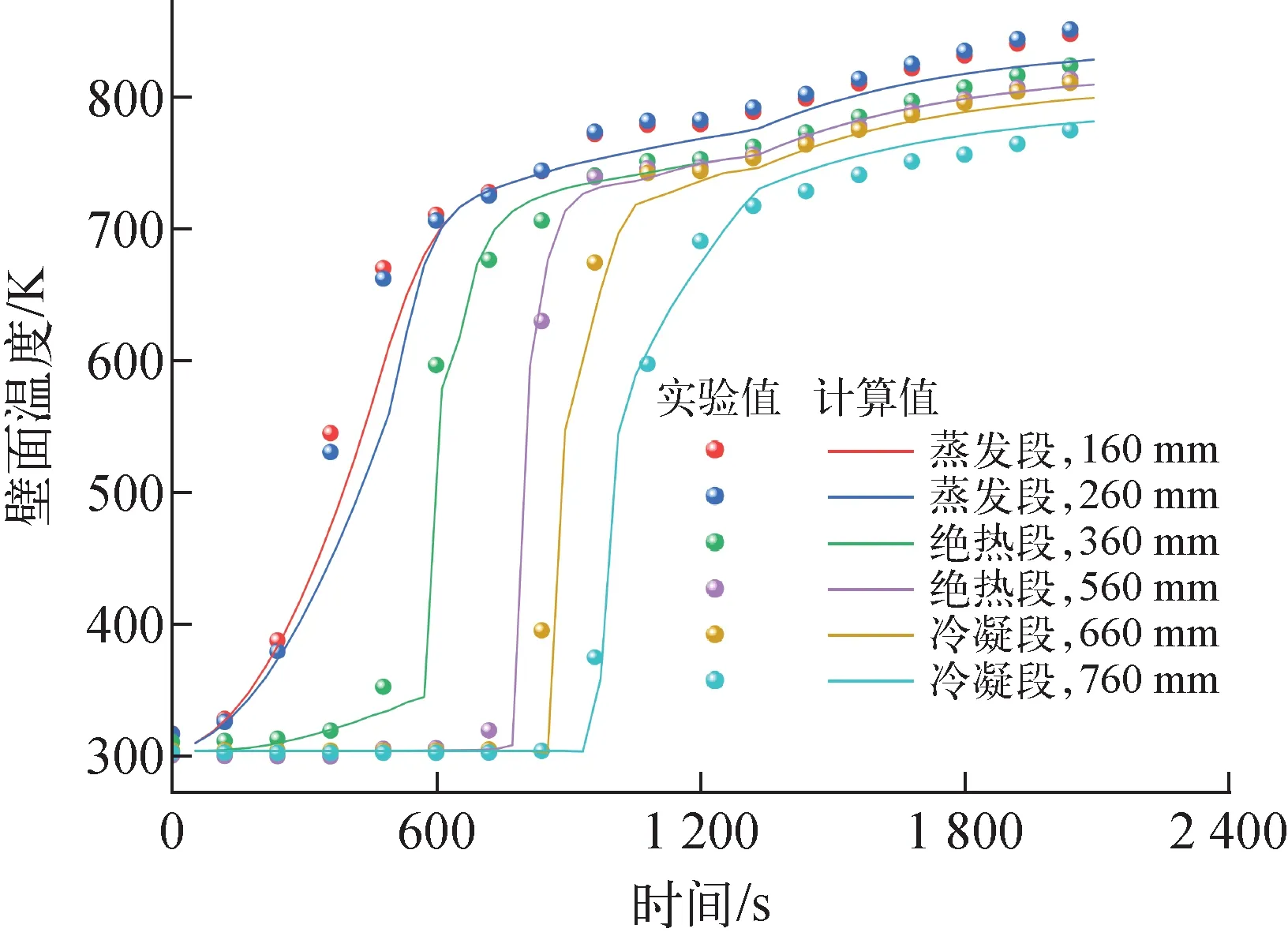
图8 热管壁面温度验证Fig.8 Verification of heat pipe wall temperature

3.3 统计结果分析

图9为HEART计算结果统计直方图,其中曲线为频率密度曲线,满足正态分布。输出结果包括燃料峰值温度、包壳峰值温度、基体温度、热管蒸发段温度和热管冷凝段温度,其中燃料峰值温度、包壳峰值温度和基体温度的结果均远低于其温度限值。热管蒸发段和冷凝段峰值温度的平均值分别为1 216.30 K和1 159.02 K,其中,热管蒸发段温度大部分处于1 075～1 375 K之间,热管冷凝段温度大部分处于1 025～1 325 K之间,均远小于热管管壁材料的温度限值(1 473.15 K),但仍有约0.67%的概率出现超过热管温度限值的情况。因此从热工角度来说,为降低热管失效概率,需要降低各输入参数的不确定性,或对现有热管反应堆的设计进行相应优化。

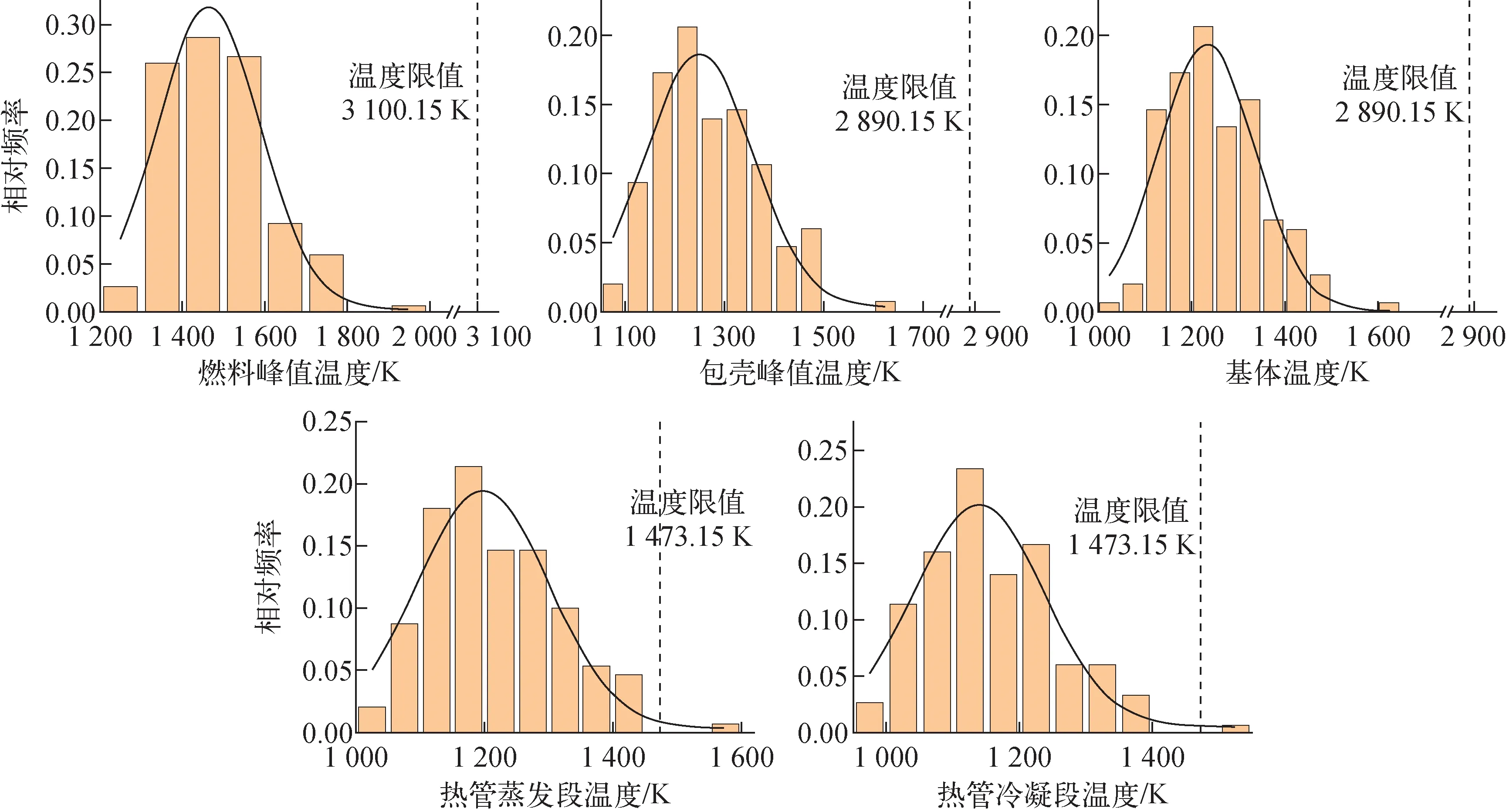
图9 HEART程序计算结果统计Fig.9 Statistic result of HEART

图10为各输入参数的不确定性对热管蒸发段峰值温度的影响,其中P为反应堆功率,λ为燃料热导率,dc为包壳厚度,δ为气隙宽度,l为热管蒸发段长度,dm为基体厚度,下标0表示该变量的参考基准值。从图10可看出,燃料热导率的不确定性与热管蒸发段峰值温度呈现明显的线性负相关,而其余参数的不确定性对热管蒸发段峰值温度的影响并不显著。

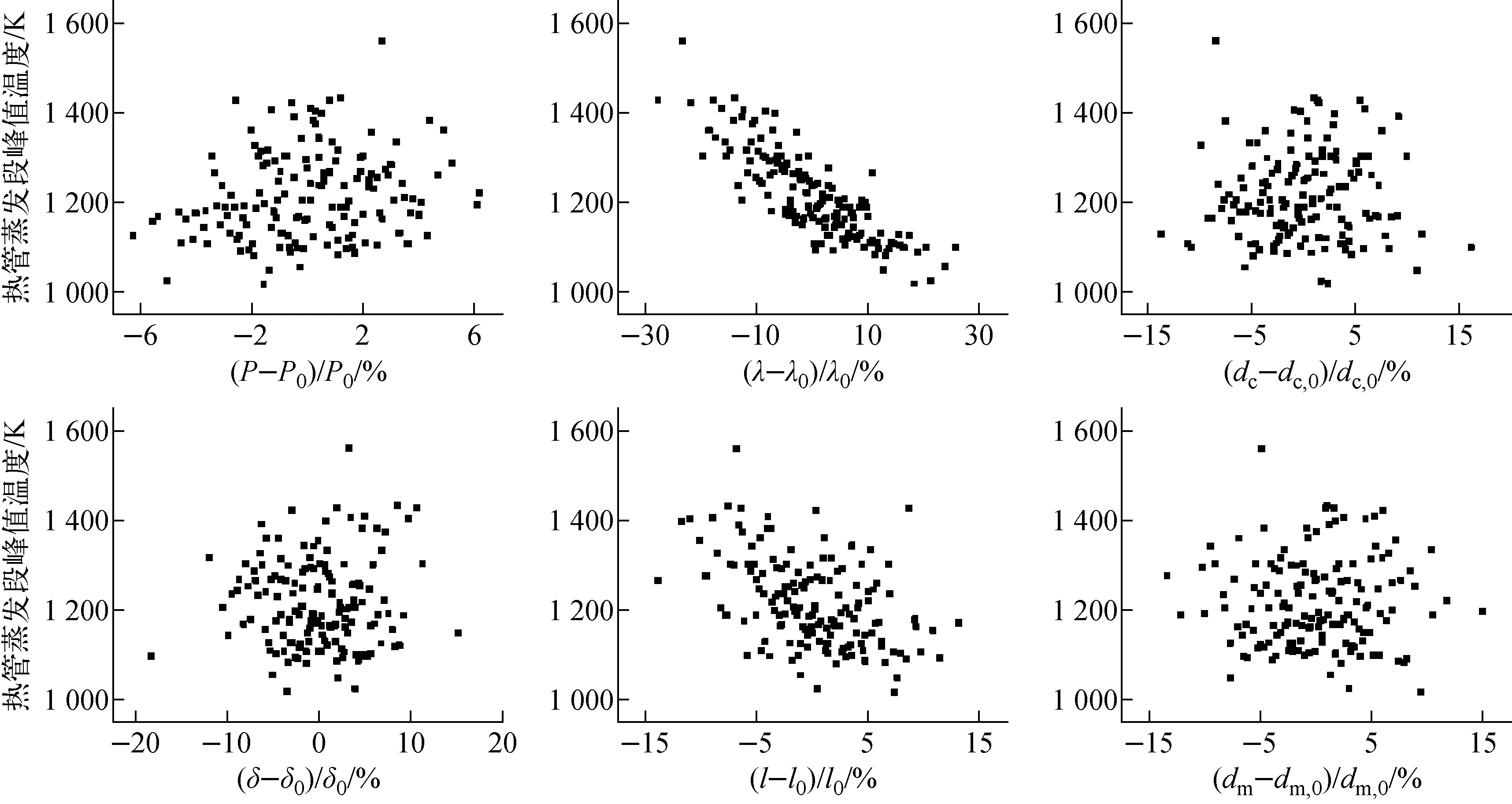
图10 输入参数不确定性对热管蒸发段峰值温度的影响Fig.10 Effect of input parameters’ uncertainty on heat pipe evaporator peak temperature

利用相关系数可对各输入参数的不确定性对热管蒸发段峰值温度的影响进行更准确的量化分析,相关系数计算公式如下:

(3)

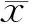
相关系数的取值在-1～+1之间,相关系数为正表示正相关,相关系数为负表示负相关。相关系数的值越接近0,越不相关。根据经验[24]可利用相关系数绝对值的大小对变量的相关程度进行划分,当相关系数绝对值位于0.01～0.29之间时为弱相关,位于0.30～0.69时为中等相关,位于0.70～1.00时为强相关。

图11为各输入变量与热管蒸发段峰值温度的相关系数,反映了各输入变量对热管蒸发段峰值温度的影响程度。可看出,燃料热导率对热管蒸发段峰值温度的影响很强且为负相关,热管蒸发段长度对热管蒸发段峰值温度影响程度中等且为负相关,运行功率与热管蒸发段峰值温度呈正相关且影响较弱,而气隙宽度、包壳厚度和基体厚度对热管蒸发段峰值温度几乎没有影响。

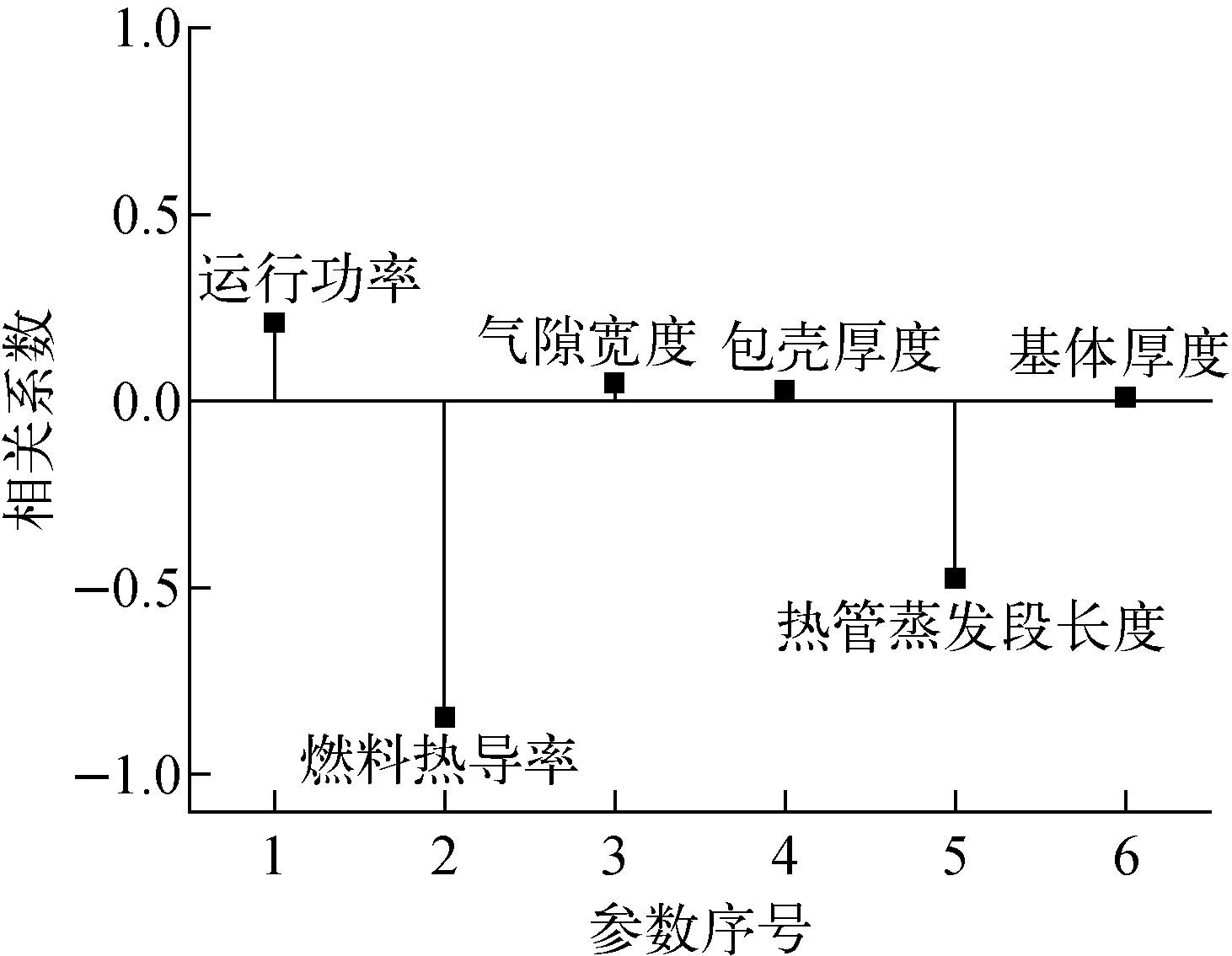
图11 输入参数与热管蒸发段峰值温度的相关性Fig.11 Correlation between input parameter and heat pipe evaporator peak temperature

此外,分析发现,同一输入变量与不同目标参数的相关系数基本相同,即输入变量的不确定性对不同目标参数的影响相同。这是因为与其他反应堆不同,热管反应堆采用固态堆芯设计,堆芯不存在对流换热,在分析堆芯换热时只需考虑导热与辐射换热,且与导热相比辐射换热的影响相对较小,可将热管反应堆堆芯视为一个纯导热模型。因此,上述关于各输入变量对热管蒸发段峰值温度影响的分析可推广到其余4个目标参数。

4 结束语

本文使用统计抽样法对热管反应堆进行了不确定性分析。利用DAKOTA程序采用LHS方法进行抽样,运用热管反应堆单通道热工分析程序进行计算,分别研究了运行功率、燃料热导率、气隙宽度、包壳厚度、热管蒸发段长度以及基体厚度的不确定性对热管反应堆运行的影响。结果表明,热管蒸发段温度和热管冷凝段温度均有0.67%的概率超过热管管壁温度限值1 473.15 K。此外,不确定性分析结果表明,输入变量的不确定性对不同目标参数的影响相同,燃料热导率的不确定性对所选的5个目标参数的影响最为显著。本文可为热管反应堆的进一步优化及后续研究方向提供参考。