双圈图补图的距离谱半径*

李远菁，李 丹，刘 康

(新疆大学数学与系统科学学院，新疆乌鲁木齐 830017)

0 引言

设G=(V(G),E(G)) 是一个简单连通图, 其中V(G) 是图G 的顶点集, E(G) 是图G 的边集.图G 的顶点数定义为n=|V(G)|, 边数定义为m=|E(G)|.图G 的补图为Gc=(V(Gc), E(Gc)), 其中V(Gc)=V(G),E(Gc)={vivj|vivj/∈E(G), ∀vi, vj∈V(G)}.设vi, vj∈V(G), 若vivj∈E(G), 则vi, vj在图G 中相邻, 记作vi～vj; 否则vi, vj在图G 中不相邻, 记作vi≁vj.图G 中与点v 相邻的顶点集称为点v 在图G 中的邻集, 记作NG(v).NG[v]=NG(v)∪{v} 称为点v 在图G 中的闭邻集.dG(v)=|NG(v)| 称为点v 在图G 中的度.点vi和vj之间最短路径的长度称为点vi和点vj在图G 中的距离, 记作dG(vi,vj).图G 中任意两点之间距离的最大值称为图G 的直径,记作diam(G).图G 的邻接矩阵为A(G)=(aij)n×n,其中当vi～vj时, aij=1,否则aij=0.图G 的距离矩阵为D(G)=(dG(vi,vj))n×n.图G 的距离特征多项式为PG(λ)=|λIn-D(G)|.距离矩阵D(G)的特征值集合称为图G 的距离谱, 记λ1(D(G))≥λ2(D(G))≥···≥λn(D(G)) 是图G 的距离谱的一个排序.矩阵M 特征值的模的最大值称为矩阵M 的谱半径.显然, 图G 的距离矩阵D(G) 是非负不可约的, D(G) 的最大特征值就是图G 的距离谱半径, 记作ρ(G).

相对图的距离谱研究, 图的补图的距离谱研究很少.在n 阶树的补图中, Lin 等[7]刻画了距离谱半径分别达到最大和最小的极图, 并且刻画了最小距离特征值分别达到最大和最小的极图; Qin 等[8]在n 阶单圈图的补图中刻画了距离谱半径达到最大的极图, 且给出了直径为3 的单圈图的补图的最小距离特征值达到最大的极图.

本文主要研究n 阶双圈图的补图的距离矩阵,在Bn中不考虑图D3,0,3,D3,0,3u(n-5),θ2,1,2,θ2,2,2和θ2,1,2u(n-4).设G 是一个n 阶连通图且Gc连通,若diam(G)≥4,则D(Gc)=Jn-In+A(G),否则D(Gc)≥Jn-In+A(G).令S={G|G ∈Bn, n ≥7, diam(G)=3 且D(Gc)＞Jn-In+A(G)}, 则S 中共有21 类图, 见图1.

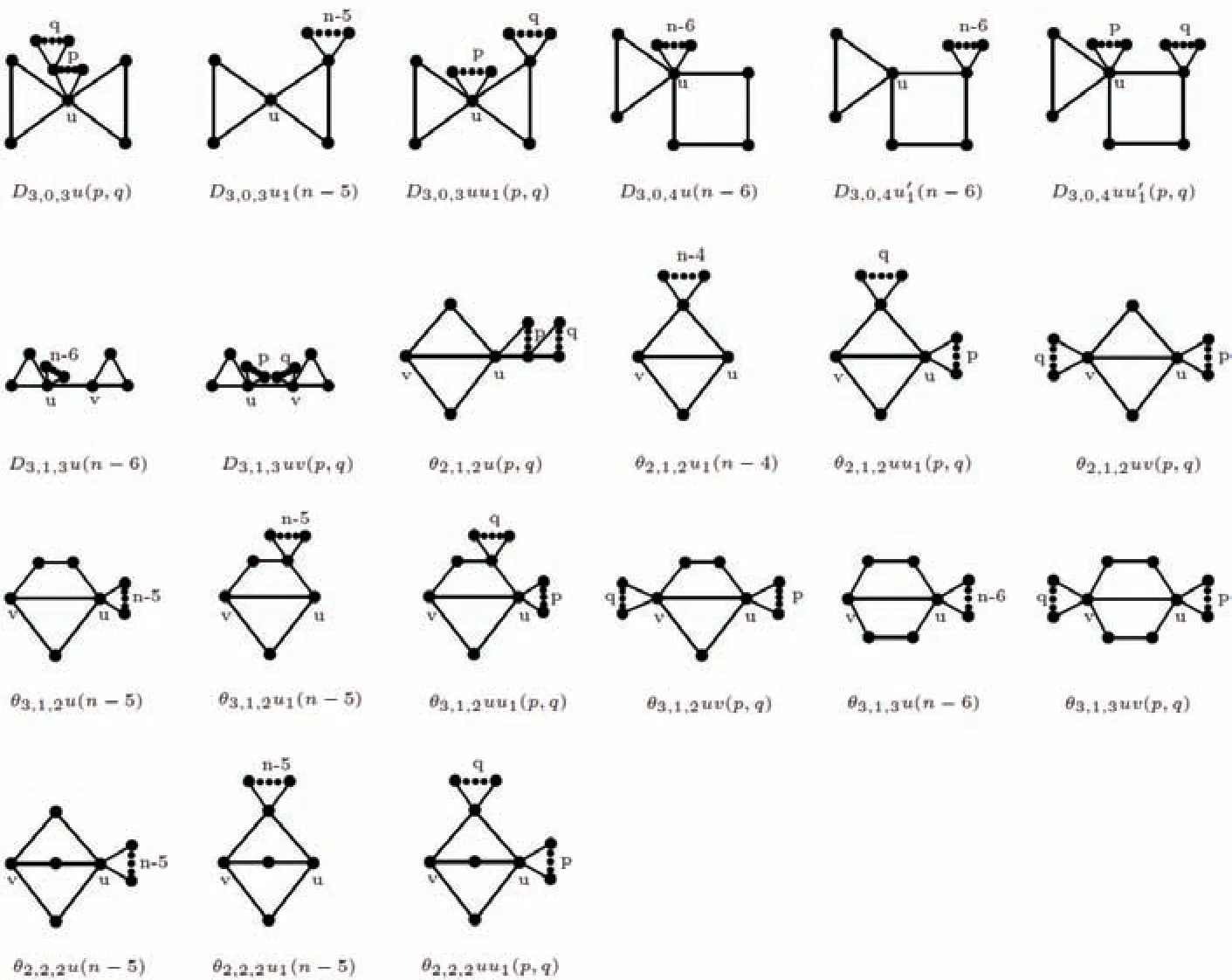
图1 S 中的21 类图

1 预备知识

引理1[9]若M 是n 阶非负不可约矩阵且n ≥2, 那么以下命题成立:

（1）矩阵M 的谱半径ρ(M)≥0 且ρ(M) 是矩阵M 的单根;

（2）矩阵M 有属于特征值ρ(M) 的正特征向量;

（3）矩阵M 的所有非负特征向量都属于特征值ρ(M).

引理2[10]设M=(mij) 是一个n 阶非负矩阵, ρ(M) 是距阵M 的谱半径, Ri(M) 表示矩阵M 第i 行的行和.则

如果M 是不可约矩阵, 那么等号成立当且仅当R1(M)=R2(M)=···=Rn(M).在本节中, 将给出两种图变换来帮助完成本文.

引理3[8](图变换1) 设图G 是一个连通图, uv 是图G 的一条非悬挂割边.设图G1是通过收缩图G 的边uv 为一点u 并使点u 与点v 连接成悬挂边得到的图, 如图2 所示, 则ρ(Gc1)＞ρ(Gc).

图2 图G 和图G1

2 主要结果

引理5 设图G ∈Dn(Dn∩S), X 是属于ρ(Gc) 的Perron 向量.对于任意的正整数n ≥7, 必然存在G′∈Θn, 若图G′c是连通图, 则ρ(G′c)＞ρ(Gc).

情形5 h ≥4, k ≥2, l=1.对图G 圈上的任意两点运用图变换2, 通过比较这两点对应于ρ(Gc) 的Perron向量中分量的大小, 将分量较小的点连接的邻边去掉并使分量较大的点与这些邻点相连, 不断进行上述的图变换, 最终可得图G3∈Θ2,1,2(情形1 中的图) 或图G4∈Θ2,2,2(情形2 中的图) 或图G5∈Θ3,1,2(情形3 中的图)或图G6∈Θ3,1,3(情形4 中的图).由引理4 可知结论成立.

情形6 h ≥3, k ≥2, l=2.不断对图G 进行与情形5 类似的图变换, 最终可得图G7∈Θ2,1,2(情形1 中的图) 或图G8∈Θ2,2,2(情形2 中的图) 或图G9∈Θ3,1,2(情形3 中的图) 或图G10∈Θ3,1,3(情形4 中的图).由引理4 可知结论成立.

情形7 h ≥k ≥l ≥3.不断对图G 进行与情形5 类似的图变换, 最终可得图G11∈Θ2,1,2(情形1 中的图) 或图G12∈Θ2,2,2(情形2 中的图) 或图G13∈Θ3,1,2(情形3 中的图) 或图G14∈Θ3,1,3(情形4 中的图).由引理4可知结论成立.

综上所述, 必然存在图G′′∈S, 使得ρ(G′′c)＞ρ(Gc).

引理7 对于任意正整数n ≥6, p, q.则ρ(θc2,1,2uv(p,q))＞ρ(θc2,1,2u(p,q)).

证明令S2=Nθ2,1,2u(p,q)(u′){u}.设X 是属于ρ(θc2,1,2u(p,q)) 的Perron 向量, 若xv≥xu′, 则

其中