基于CEEMDAN-VMD-LSTM的超高频金融时间序列预测

闫勇志 沐年国

摘  要： 对超高频金融数据的预测，模态分解降低了数据的噪声，提高了数据预测精度。据此提出了自适应噪声的完整集合经验模态分解（CEEMDAN）与变分模态分解（VMD）相结合的二次分解模型。先将期货日度行情数据通过CEEMDAN一次分解，并通过样本熵将分解后的序列整合成高频、低频和趋势序列；再将高频和低频序列分别进行VMD分解，然后将各个IMF分量通过LSTM网络预测，最终整合各个预测结果。模型各项指标均好于一次分解。

关键词： 超高频金融数据； CEEMDAN； VMD； 二次分解

中图分类号：TP391          文献标识码：A     文章编号：1006-8228（2023）05-102-07

UHF financial time series predicting based on CEEMDAN-VMD-LSTM

Yan Yongzhi， Mu Nianguo

（Business School， University of Shanghai for Science & Technology， Shanghai 200093， China）

Abstract： For the prediction of UHF financial data， modal decomposition reduces the noise of data and improves the accuracy of data prediction. Accordingly， a quadratic decomposition model combining the complete ensemble empirical mode decomposition for adaptive noise （CEEMDAN） and variational mode decomposition （VMD） is proposed. Firstly， the daily market data of futures are decomposed by CEEMDAN， and the decomposed series are integrated into high-frequency， low-frequency and trend series by sample entropy. Then， the high-frequency and low-frequency series are decomposed by VMD respectively， and each IMF component is predicted by LSTM network. Finally， the prediction results are integrated. Compared with CEEMDAN decomposition and VMD decomposition， each index of the proposed model is better.

Key words： UHF financial data; CEEMDAN; VMD; quadratic decomposition

0 引言

超高頻金融数据是根据市场上的每一笔交易来进行采集，时间间隔不固定，具有非平稳、非线性以及高度复杂的特征[1]。如何准确掌握日内超高频数据是量化投资领域的重大课题之一。

金融高频数据的预测主要方法是通过神经网络进行预测，Hajiabotorabi等[2]采用基于B样条小波多分辨率改进DWT-RNN模型，结果表明，BS3-RNN预测模型比使用其他小波或神经网络模型具有更好的预测能力，但是RNN模型有梯度消失问题，因此Bukhari等[3]提出了ARFIMA-LSTM模型，不仅最小化了波动性问题，而且克服了神经网络的过拟合问题。

金融高频数据含有大量噪声，诸多学者采用小波降噪法对金融数据进行处理。Huang[4]提出了经验模态分解方法，引入复杂数据集的瞬时频率，消除了表示非线性和非平稳信号的杂散谐波的需要。Afolabi et al[5]利用EMD方法结合LSTM神经网络对苹果公司股价进行预测；但是EMD会造成模态混叠的问题，Huang and Wu[6]提出了一种基于集成经验模式分解（EEMD）的算法，有效遏制EMD模态混合问题，Yeh等[7]提出互补集合经验模式分解（CEEMD）克服了EEMD重构误差大、分解完备性差的问题。Torres[8]提出自适应噪声的完整集合经验模态分解（CEEMDAN）固有模态分量中残留噪声更少，有效减少重构误差，分解效率最高。冯晓天[9]年提出CEEMDAN-SSA-LSTM方法，基于1分钟收盘价高频数据的CEEMDAN-SSA-LSTM模型是预测效果最好的模型。

Konstantin Dragomiretskiy[10]提出一种变分模态分解（VMD）方法，一种自适应、非完全递归的非线性分解方法，可以实现分解模态的同时提取，有效地将时间序列中混入的高斯白噪声分离，实现信号的降噪处理。史心怡[11]改进类经验模态分解-LSTM-Adaboost组合模型对股市波动率预测研究，结果表明VMD的分解精度优于EEMD。

近年很多学者考虑二次分解技术，以求提高模型的预测精度，程文辉等[12]提出二次分解与LSTM的金融时间序列预测算法，将VMD和EEMD相结合，将VMD分解后的残余分量二次处理，结果表明，二次分解算法有效提升模型的预测能力。何荣辉[13]年提出多元预测模型对短期风电功率进行预测研究，通过CEEMDAN一次分解后，将波动大的IMF分量进行VMD分解，二次分解后的预测结果好于对比模型。唐莉[14]提出混合分解集成模型对碳排放权价格进行研究，首先通过CEEMDAN对序列进行一次分解，然后通过计算IMF模糊熵值，将模糊熵值大的分量进行VMD分解，结果表明二次分解好于其他模型。Feite Zhou等[15]总结了两个基本的CEEMDAN-LSTM框架，并提出了一种与VMD相结合的混合框架对碳价格进行预测研究，结果表明，二次分解技术能够提高一次分解的预测精度。

综上所述，对非平稳、非线性的时间序列数据，基于CEEMDAN和VMD的二次分解方法具有较好的预测效果。因此本文提出CEEMDAN-VMD-LSTM对超高频金融数据进行研究，主要贡献有：

⑴ 通过样本熵重构高频序列和低频序列，对两个序列分别进行VMD分解，充分利用CEEMDAN和VMD分解，并且对比单变量回归和多变量回归结果，结果表明对高频和低频序列都进行二次分解后，单变量回归模型略好；

⑵ 期货行情数据，即超高频数据的研究较少，本文提出的预测方法，为期货量化交易，提出了新的方向。

1 研究方法

1.1 CEEMDAN

具有自适应噪声的完全集成经验模态分解（CEEMDAN）是由EMD、EEMD和CEEMD发展而来的。定义[EMDn·]为应用 EMD 算法产生的第[n]个阶段的模态分量，CEEMDAN算法产生的第[n]个模态分量记为[IMFn]该算法的实现过程如下：

（a） 将待分解的信号[ft]添加[ n]次均值为0的高斯白噪声序列，构造共[n]次实验的待分解序列[fit]。

[fit=f（t）+ε0ωi（t），i=（1，2，...，n）]  ⑴

其中，[ε0]为信噪比，[ωi（t）]为第i次添加的白噪声序列

（b） 对每一个[fit]应用EMD算法进行分解，得到第一个模态分量（IMF）及第一个唯一残余分量[r1（t）]：

[IMF1（t）=1ni=1nIMFi1（t）=1nEMD1（fi（t））]

[r1（t）=f（t）-IMF1（t）]  ⑵

（c） 将分解后得到的残余分量添加噪声继续应用 EMD进行分解。

[IMFk（t）=1ni=1nEMD1（rk-1（t）+εk-1EMDk-1（ωi（t））），k=2，3...，n]

[rk（t）=rk-1（t）-IMFk（t）]  ⑶

（d） 最后，当残差不超过两个极值点且不能继续分解时，终止CEEMDAN算法。此时，残差趋势明显而直接，原始信号序列被分解为n个模态分量和残差项[R（t）]：

[ft=k=1nIMFkt+Rt] ⑷

1.2 样本熵

样本熵可以评价时间序列数据的系统复杂度，是对近似熵的改进。以和的对数计算，以减少近似熵误差。与近似熵相比，样本熵的计算不依赖于数据长度，具有更好的一致性。一般来说，序列的样本熵越大，表示序列越复杂。

（a） 设[n]为数据点总数，[m]为待比较序列的长度，则向量[xmi]可表示为：

[xmi=xi，x（i+1），..，x（i+m-1），i=1..，n-m+1] ⑸

（b） 定义（a）中两个向量之间的距离为

[dmxm（i），xm（j）=max[xm（i+k）-xm（j+k）]，0≤k≤m-1] ⑹

（c） 给定阈值r，统计[dmxm（i），xm（j）≤r]的个数记为[νm]，增加维度至[m+1]，统计[dm+1xm+1（i），xm+1（j）≤r]的个数记为[ωm+1]。

（d） 确定匹配点的概率，[Bmr]为[m]维概率，[Amr]为m+1维概率：

[Bmr=1n-mi=1n-mvmin-m+1Amr=1n-mi=1n-mwm+1in-m+1]   ⑺

（e） 样本熵定义为[S（m，r）]：

[Sm，r=limn→∞（-lnAmrBmr）] ⑻

当n为有限值时，样本熵可用以下公式估计：

[Sm，r，n=-lnAmrBmr] ⑼

1.3 VMD

VMD是一种信号分解方法，在得到分解分量的过程中，通过迭代搜索变分模型的最优解，确定各分量的中心频率和有限带宽，从而自适应地实现信号的频域划分和各分量的有效分离。VMD将每个分量的估计带宽之和最小化，并使用交替方向乘子法提取相应的中心频率。

VMD的核心思想是构建和求解变分问题。需求解的约束变分优化问题如式：

[minuk，wkk∥?t（δt+jπt）*ukte-jwkt∥22]   ⑽

[s.t.k=1Kuk（t）=f（t）] ⑾

其中，[uk]输入信号分解后第k个模态函数，[wk]为中心频率，[K]为需分解的模态数量[δt]为单位脉冲函数，[f（t）]为原始信号。

（a） 为了解决优化问题，引入拉格朗日乘数和二阶惩罚因子[α]，然后将约束变分问题转化为无约束变分问题，得到增广拉格朗日表达式：

[Luk，wk，λ=αk∥?t（δt+jπt）*ukte-jwkt∥22]

[+∥f（t）-kuk（t）∥22+λt，f（t）-kuk（t）] ⑿

（b） 利用交替方向乘子法計算鞍点即原问题最优解，求解[uk]、[wk]和[λ]

[un+1kw=f（w）-i≠kui（w）+λw/21+2αw-wk2]  ⒀

其中，[un+1kw]、[uiw]、[fw]、[λw]是[un+1kw]、[uiw]、[fw]、[λw]的傅里叶变换。

（c） 更新[wk]

[wn+1k=0∞w|un+1k（w）|2dw0∞|un+1k（w）|2dw] ⒁

（d） 更新[λ]

[λn+1（w）=λn（w）+τf（w）-kun+1k（w）] ⒂

其中，[τ]为噪声的容忍度。

重复上述步骤直到满足迭代条件。

1.4 LSTM

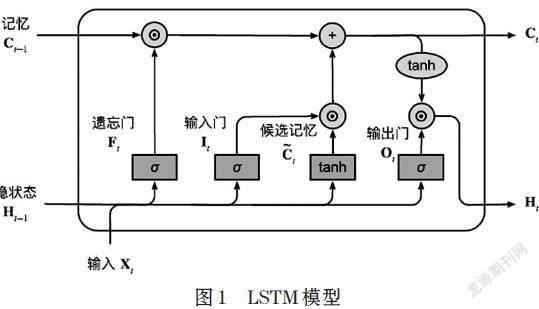
LSTM模型在图像数据处理中，其主要可以缓解梯度消失和梯度爆炸，模型由三部分组成，如图1所示，分别为输入门、遗忘门和输出门。

LSTM模型的数学表达如公式⒃：

[It=σ（XtWit+Ht-1Whi+bi）Ft=σ（XtWxf+Ht-1Whf+bf）Ot=σ（XtWxo+Ht-1Who+bo）Ct=tanh（XtWxc+Ht-1Whc+bc）Ct=Ft⊙Ct-1+It⊙CtHt=Ot⊙tanh（Ct）] ⒃

其中，[Ht-1]为前一步时间隐状态，[Wxi]等为权重，[bi]等為偏置项，[Ct]为输出

2 数据处理

2.1 数据采集

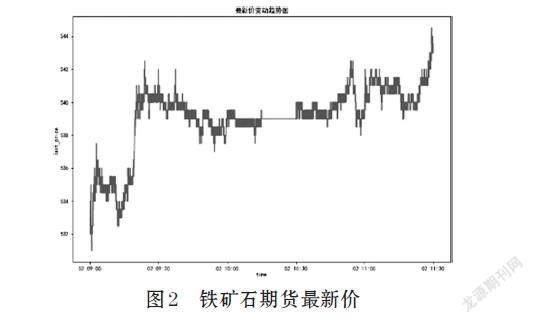
文章选取大连商品交易所，铁矿石主力期货，2018年1月2日9：00-11：30的最新价作为研究对象。9：00-11：30共有15684个数据。最新价变动趋势如图2所示。

2.2 数据分析

2.2.1 平稳性检验

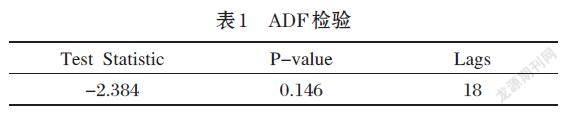
通过Python 中Statsmodels模块中的函数，使用增强的Dickey-Fuller（ADF）测试来测试数据的平稳性，如表1所示p值为0.146大于0.05，因此接受原假设，认为数据是非平稳序列。

2.2.2 自相关检验

LB（Ljung-Box）统计量检验序列自相关性，p值为0小于0.05，拒绝原假设，表明数据具有很强的自相关性。

使用Statsmodels模块计算自相关函数（ACF）和偏自相关函数，如图3所示， PACF显著拖尾性，显示了最新价的自相关关系。

2.2.3 正态性检验

JB（Jarque-Bera）统计量检验序列正态性，偏度为-1.25，峰度为1.229，p值为0小于0.05，拒绝原假设，序列不服从正态分布。

3 模型建立

3.1 模型评价指标

本文采用均方根误差RMSE、R Squared、平均绝对误差MAE、平均绝对百分比误差MAPE以及准确率作为评价指标。RMSE、MSE、和MAPE反应了预测值和真实值得偏差，数值越小模型拟合越优；R Squared和准确率反应了模型的拟合优度，数值越接近1，拟合效果越好。计算公式如下

[RMSE=1Ni=1Nyi-yi2] ⒄

[R2=1-i=0myi-yi2i=0myi-yi2]   ⒅

[MAE=1Ni=1N|yi-yi|]   ⒆

[MAPE=1Ni=1N|yi-yiyi|*100%] ⒇

对于准确率（ACC）的计算，铁矿石主力期货数据最小变动单位为0.5，且数据仅有一位小数；将预测的数据与真实数据做差，如果两者之差的绝对值小于等于0.25，则认为预测值与真实值相等。

3.2 CEEMDAN分解与样本熵

基于第1章的数学理论，本文使用PyEMD信号模块中的CEEMDAN函数对铁矿石主力期货1月2日上午最新价数据进行分解。图4（a）显示了13个IMF从上到下的分解结果。横轴表示最新价的时间序列号，纵轴表示单位为元的每个部分的价值。序列的频率和复杂性逐渐降低，变化模式比原始序列更直观，整体价格趋势也更明显。

Python中sampen模块使用样本熵来度量每个IMF的复杂性。基于Wang等[16]人的研究，整合具有相似样本熵值的IMF可以适当减少计算量，增加建模速度，减少过拟合。在图4（b）中无论m和r的取值如何，第二个和第三个IMF分量的样本熵值均高于其他分量所对应的值，这代表了一种复杂的、易变的模式；同时第6-13个IMF分量，复杂性波动性很小。因此，这13个IMF可以集成为三个新的合作固有模式函数（Co-IMF）：高频序列Co-IMF0（IMF1-2）、低频序列Co-IMF1（IMF0、IMF3-4）和趋势序列Co-IMF2（IMF5-12）。这三个Co-IMF的变化模式相对规则且直接，这便于进一步提取每个IMF的波动特征并训练预测模型。在实际的建模过程中选取m=1，r=0.1参数进行建模，聚类过程如图4（c）所示。

3.3 VMD分解

为了准确预测高频序列，本文利用二次分解方法对高频序列进行进一步分解。参考Li等[17]人的文献，使用一种称为变分模态分解（VMD）的信号分解方法。

避免数据分解出现欠分解和过分解，需要确定序列分解的[K]值，令[K=2，3，...，13]分别进行分解，计算中心频率，每个[K]值对应的最后频率随K值增加，中心频率逐渐平稳，因此选取[K=10]作为VMD模型分解的参数，其他参数使用默认参数。

由于EMD、EEMD和CEEMDAN都来自EMD，使用它们来重新分解高频序列不能获得良好的结果。如表2所示，对于高频序列数据（Co-IMF0）VMD分解后进行预测的结果RMSE、MAE和MAPE指标均好于CEEMDAN分解和不分解。表明二次分解采用VMD分解能够将复杂数据分解，模型能够取得较好的效果。

3.4 CEEMDAN-VMD-LSTM

根据3.2节和3.3节的分析，设计一个CEEMDAN-VMD-LSTM模型对期货日度高频最新价进行预测。具体步骤如下：

⑴ 数据处理后进行CEEMDAN分解，得到若干IMF分量。

⑵ 计算⑴中的IMF分量的样本熵，聚类整合成高频序列Co-IMF0、低频序列Co-IMF1和趋势序列Co-IMF2。

⑶ 将高频序列Co-IMF0进行VMD分解，并通过LSTM模型预测

⑷ 将低频序列Co-IMF1进行VMD分解，并通过LSTM模型预测

⑸ 將趋势序列Co-IMF2直接通过LSTM模型预测。

⑹ 整合三个预测的序列，并分析相关指标。

4 实验

4.1 参数设置

铁矿石主力期货序列数据包含15684个样本点，将10：45-11：30数据作为测试集，9：00-10：45数据作为训练集，即2/3数据用于训练，1/3数据用于测试。时间步长选取10，即选取10个数据预测下一时刻数据。

4.2 对比模型

为了验证模型的可行性，选取六种模型对比：

模型1（LSTM）：将期货数据序列直接通过LSTM神经网络预测。

模型2（EMD-LSTM）：将期货序列进行EMD分解后，每个IMF分量分别通过LSTM网络预测，最终整合各个分量。

模型3（CEEMDAN-LSTM）：将期货序列进行CEEMDAN分解后，每个IMF分量分别通过LSTM网络预测，最终整合各个分量。

模型4（VMD-LSTM）：将期货序列进行VMD分解后，每个IMF分量分别通过LSTM网络预测，最终整合各个分量。

模型5（CEEMDAN-VMD-LSTM多变量）：将期货序列数据，通过CEEMDAN一次分解后，采用样本熵聚类，整合成高频、低频和趋势序列，然后对高频和低频序列进行VMD分解，将分解后的序列通过LSTM网络，多变量回归，最后将各个预测值相加。

模型6（CEEMDAN-VMD-LSTM单变量）：将期货序列数据，通过CEEMDAN一次分解后，采用样本熵聚类，整合成高频、低频和趋势序列，然后对高频和低频序列进行VMD分解，将每个IMF分量分别通过LSTM网络预测，最后将各个预测值相加。

4.3 实验结果分析

由于深度学习的预测具有一定的随机性，因此将各个模型预测10次，对指标取均值再对模型进行相应的评价，能够增加模型的可信度。

6个模型分别预测10次，各个指标取均值的结果如表3所示，图5将四个指标做了可视化展示。

如表3和图5所示，模型2通过EMD分解解决了数据不平稳的因素，各项指标均优于模型1，R2值高3.94%，RMSE值低8.28%，MAE值低5.14%，MAPE值低0.96%，ACC值高11.22%。

模型3通过CEEMDAN分解，解决了EMD分解中的模态混叠问题，各项指标均优于模型2，R2值高1.36%，RMSE值低4.42%，MAE值低4.01%，MAPE值低0.75%，ACC值高5.11%。

模型4引入VMD分解，VMD分解能够更好的分解非平稳、非线性以及复杂的数据，各项指标均好于模型3，R2值高1.47%，RMSE值低5.79%，MAE值低4.88%，MAPE值低0.88%，ACC值高3.01%。

模型6先通过CEEMDAN分解数据，再根据样本熵重构，重构后的序列再通过VMD分解，最后接LSTM网络预测，模型充分利用了CEEMDAN和VMD分解的特点，各项指标均好于模型4，其中 R2值高0.32%，RMSE值低2.1%，MAE值低1.58%，MAPE值低0.3%，ACC值高3.1%，进一步说明CEEMDAN-VMD-LSTM模型好于一次分解的EMD、CEEMDAN以及VMD模型。

5 结束语

本文提出一种基于CEEMDAN的二次分解方法，通过样本熵重构CEEMDAN分解后的序列，复杂序列通过VMD分解后，将各个分量分别通过LSTM模型预测，最终将预测结果整合。通过实验分析和模型对比，可以得出以下结论。

⑴ CEEMDAN-VMD-LSTM模型处理期货日度高频数据，具有更高的准确率，能够跟踪期货tick数据的趋势以及变化。

⑵ VMD模型处理非线性、非平稳以及复杂的数据，表现得比EMD系列更好，因此将重构的数据通过VMD模型分解，提高了模型的准确度。

未来的工作可以将期货量化研究、比如期货做市模型、高频交易等相联系。

参考文献（References）：

[1] 田聪.基于改进型EMD-LSTM的高频金融时间序列预测[D].

硕士，江西财经大学，2021

[2] Zeinab Hajiabotorabi，Aliyeh Kazemi，Faramarz Famil

Samavati，Farid Mohammad Maalek Ghaini. Improving DWT-RNN model via B-spline wavelet multiresolution to forecast a high-frequency time series[J]. Expert Systems With Applications，2019，138（C）

[3] Bukhari A H， Raja M A Z， Sulaiman M， et al. Fractional

neuro-sequential ARFIMA-LSTM for financial market forecasting[J].Ieee Access，2020，8： 71326-71338

[4] Norden E. Huang，Zheng Shen，Steven R. Long，Manli C.

Wu，Hsing H. Shih，Quanan Zheng，Nai-Chyuan Yen，Chi Chao Tung，Henry H. Liu. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings： Mathematical， Physical and Engineering Sciences，1998，454（1971）

[5] Noemi Nava，T. Di Matteo，Tomaso Aste. Anomalous

volatility scaling in high frequency financial data[J]. Physica A： Statistical Mechanics and its Applications，2016，447

[6] Wu Z， Huang N E. Ensemble empirical mode decomposi-

tion： a noise-assisted data analysis method[J].Advances in adaptive data analysis，2009（1）：1-41

[7] Yeh J R， Shieh J S， Huang N E. Complementary ensemble

empirical mode decomposition：A novel noise enhanced data analysis method[J]. Advances in adaptive data analysis，2010（2）：135-156

[8] Torres M E， Colominas M A， Schlotthauer G， et al. A

complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE international conference on acoustics， speech and signal processing （ICASSP）.IEEE，2011：4144-4147

[9] 馮晓天.基于CEEMDAN-SSA-LSTM的高频股票价格预

测研究[D].硕士，江西财经大学，2022

[10] Konstantin D， Zosso D. Two-dimensional variational

mode decomposition[C]//Energy Minimization Methods in Computer Vision and Pattern Recognition，2015，8932：197-208

[11] 史心怡.基于改进类经验模态分解-LSTM-Adaboost组

合模型对股市波动率预测研究[D].硕士，上海师范大学，2022

[12] 程文辉，车文刚.基于二次分解与LSTM的金融时间序列

预测算法研究[J].重庆邮电大学学报（自然科学版），2022，34（4）：638-645

[13] 何荣辉.基于多元预测模型的短期风电功率预测研究[D].

硕士，广西大学，2022

[14] 唐莉.基于混合分解集成模型的碳排放权价格的实证研究[D].

硕士，山东大学，2021

[15] Zhou Feite，Huang Zhehao，Zhang Changhong. Carbon

price forecasting based on CEEMDAN and LSTM[J]. Applied Energy，2022，311

[16] Wang Jujie，Sun Xin，Cheng Qian，Cui Quan. An

innovative random forest-based nonlinear ensemble paradigm of improved feature extraction and deep learning for carbon price forecasting[J]. Science of The Total Environment，2020，762（prepublish）

[17] Li Hongtao，Jin Feng，Sun Shaolong，Li Yongwu. A new

secondary decomposition ensemble learning approach for carbon price forecasting[J].Knowledge-Based Systems，2021，214（prepublish）