基于注意力机制的多级监督人群计数算法

王勇杰 王少坤 朱姜华 张晓宇

摘要：针对人群计数问题，提出了一种基于卷积神经网络的人群计数网络，该网络由主干网和多级监督分支结构组成，在主干网络的多个阶段引入注意力机制学习不同尺度的人群特征。算法采用VGG16模型的前13层作为主干网，并且加入膨胀卷积网络结构，融合图像中的多尺度人群特征，解决多尺度人群计数问题，从而生成高质量的密度图。同时，在3个不同尺度的分支结构中引入注意力机制，在损失函数中加入不同尺度的注意力损失，从而使整个网络聚焦图像中的人群区域。算法在4个主要的数据集上进行了测试，算法结果优于最近其他的方法。

关键词：人群计数；卷积神经网络；注意力机制；多级监督

中图分类号：TP391.4文献标志码：A文章编号：1008-1739（2023）06-67-6

0引言

人群计数技术可以获得图像或视频中的人群准确数量，可以用于安全监控和行为建模。在广场、景区等公共场所，人群计数的结果对一系列社会治安问题的预警具有重要作用[1-2]。因此，人群计数问题已经成为视频行人检测和分析的重要组成部分。根据分析结果，不仅可以知道图像中的总人数，还可以知道图像中人群的分布情况，从而可以有效防止一些潜在危险事件的发生。

较早的人群计数方法一般采用基于检测的方式，利用行人检测窗口[3]对图片中的行人进行检测，从而获得行人总数。过程中，为了解决图像中存在的遮挡问题，进一步提出了基于回归的方法[4]。这种方法的主要思想是学习行人特征与行人总数之间的映射关系。随着深度学习技术的快速发展，基于人群密度估计的方法被广泛应用于人群计数任务中。

本文也采用基于密度估计的方法，在算法模型中引入多尺度行人特征和注意力机制，有效提升了人群检测准确率。

1基于人群密度估计的方法

采用人群密度估计的方式能够很好地处理图像中的遮挡和行人头部尺度变化等问题。由于卷积神经网络强大的特征学习能力，同样被研究人员用在人群密度估计的研究任务当中，并且取得了很大的进步。人群密度估计方法如图1所示。

由于图像中不同位置的人表现出不同的大小和尺寸，为了解决行人的尺度变化问题，许多研究人员已经做了大量的人群计数研究工作，这些方法包括多分支结构[5]、显式网络集合[6]、多尺度卷积网络[7]、注意机制[8]或特殊结构[9]等，这些方法都取得了显著的效果。然而，这些方法的实现通常需要复杂的结构和复杂的训练过程。

本文提出了一种由主干网和多分支结构组成的人群密度估计网络，并引入注意力机制。网络主干使用VGG16模型的前3个最大池化层。每个池化层之前增加多分支结构，利用膨胀卷积提取不同感受野的特征。同时在训练过程中，还将多分辨率注意力图产生的多尺度损失加入到损失函数中。

2本文算法

本文算法的核心是在模型训练过程中引入更多的监督，使整个网络聚焦于图像中的人群区域，从而降低图像中的背景噪声影响，网络模型利用膨脹卷积和注意力机制来生成多尺度的注意力图。最后，网络模型将主干网络不同阶段的多尺度特征融合在一起，生成最终的密度图，回归总人群数。

2.1网络结构

网络模型结构如图2所示。

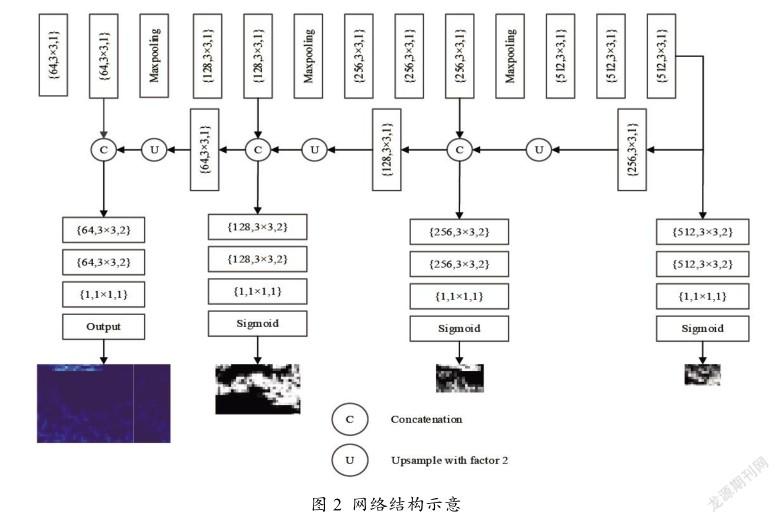
图2中的卷积层用通道数/内核大小×内核大小/膨胀率表示，C表示级联操作，U表示上采样操作。网络模型结构采用VGG16模型的一部分作为主干网络，即采用只有3×3卷积核的单主干网络用作特征提取器。由于主干网络中的卷积核尺寸较小，因此整个网络模型计算量较小，收敛速度较快。网络模型的融合特征分别来自主干网络的4个卷积层：Conv1-2、Conv2-2、Conv3-3和Conv4-3。主干网络VGG16模型有5个最大池化层，最大池化层可以通过降低图像分辨率来减少计算量。但是为了避免特征图太小，网络模型只保留前3个最大池层。网络模型为了得到充足的图像特征，网络将低层到高层的图像特征进行融合，得到最终的密度图。网络模型使用了来自ImageNet的预先训练过的VGG16模型参数，并根据人群图像进行了微调。由于预训练模型在许多具有挑战性的数据集上表现出良好的性能，因此选择了这种策略，并通过实验结果验证了模型的训练效果。

网络模型的多分支结构用来生成多尺度的注意力图，每个分支中采用膨胀卷积扩大卷积感受野，从而提取不同尺度的图像特征。膨胀卷积可以获得比正常卷积更大的感受野，并利用正常卷积进一步得到特征图。多分支结构利用多尺度信息从局部到全局降低图像的背景噪声。多分支结构的输出是注意力图。在训练过程中，采用不同分辨率的注意力图（原始输入图像分辨率的1/4、1/16、1/64）对网络进行多尺度监督。

多分支结构的末尾通过Sigmoid激活函数将融合后的特征图生成注意力图。Sigmoid激活函数可以从特征图中给出0或1的值，从而将图像背景区域和人群头部区域用注意力图区分。因此，多分支结构中的注意力图给出了融合特征图中的头部概率区域。在融合特征图中，头部的可能性区域设置为1，背景的可能性区域设置为0。在整个网络模型训练过程中，注意力图用于调整网络模型的焦点。

与以前的方法不同，很多模型算法中有太多的池化层，导致最终生成的密度图分辨率太小。过多的池化层虽然可以加速模型的计算过程和防止过拟合，还能使模型提取更高层的特征信息，但在降低分辨率的过程中会丢失一些空间信息。因此模型使用上采样操作将密度图的大小恢复到原始输入的大小，从而增加更多的图像细节信息。此外，在每一次级联操作之前，采用膨胀卷积从局部到全局得到图像中的前景（人群区域），然后利用前景和真值密度图计算注意力损失。由于从高层次提取的特征比从低层次提取的特征更具鉴别能力，因此模型对由高层次特征生成的密度图赋予了更高的权重。

因此，该模型的整个流程是：将输入图像输入到模型中，通过主干网络进行特征提取获得特征图。将获取的特征图通过多分支结构得到级联的特征图，同时利用注意力机制生成多尺度的注意力图，在网络模型的多个阶段进行监督。由于批训练和批归一化可以稳定训练过程，加速模型损失收敛，所以在每个卷积层之后都应用了批归一化。除了最后一层，模型在每个卷积层之后添加ReLU激活操作。

2.2密度图

2.5参数训练

在训练过程中，为了避免数据冗余，只从输入图像的任意位置随机裁剪固定大小。根据不同的数据集，裁剪的尺寸大小是不同的。裁剪后的图像以概率0.5随机水平翻转，并用概率为0.3的参数0.5～1.5进行伽玛对比度变换，达到数据增强的目的。由于UCF-QRNF数据集中的图像分辨率很高，将这些数据集中的所有图像调整为1 024 pixel×768 pixel。如上所述，真值注意力图的分辨率大小调整为原始图像的1/4、1/16、1/64。

对于网络模型的主干网络，使用来自ImageNet的预先训练的模型来初始化。模型的其他卷积层用高斯函数初始化，标准差为0.01。算法模型使用具有固定学习率1×10-4的Adam来优化网络。批量大小设置为4，采用英伟达RTX 2080TI的GPU来加速计算过程。算法模型采用的软件框架是Pytorch 1.1.0。

3实验

算法模型已经在4个公开的具有挑战性的数据集（ShanghaiTech、UCF-QRNF、WorldExpo10和UCF_CC_50）上进行了大量实验，实验结果证明了算法模型的有效性。

3.1评价标准

3.2数据集

3.2.1 ShanghaiTech数据集

该数据集由文献[5]提出，共包含1 198幅图像，分为两部分：PartA和PartB。PartA包含的482张图片都来自互联网，其中300张用于训练，182张用于测试。PartB包含的716张图像都来自上海街头的监控，其中400张用于训练，316张用于测试。在训练过程中，PartA数据集中的图像裁剪大小为300 pixel×300 pixel，PartB中图像的裁剪大小为512 pixel×512 pixel。

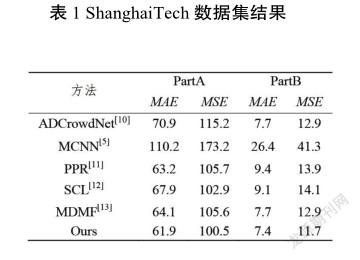
将算法模型的实验结果与其他最近的方法进行了比较。如表1所示，算法模型的实验结果是所有比较方法中最好的。与排名第二的模型相比，模型的实验结果使PartA的MAE提高了1.3，PartB的MAE提高了0.3，PartB的MSE提高了1.2。

3.2.2 UCF_CC_50数据集

该数据集包含50幅图像，由文献[19]提出的。由于数据集中的图像数量较少，且图像中人群分布不均匀，因此该数据集具有很大的挑战性。由于图像数量较少，采用了5折交叉验证的方法来评估算法模型。在训练过程中，此数据集中的图像裁剪大小为300 pixel×300 pixel。

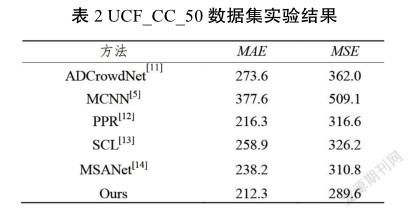
实验结果如表2所示。从表2可以看出，在MAE和MSE方面，本算法模型取得了最好的实验结果。与排名第二的模型相比，该方法的MAE提高了25.9，MSE提高了21.2。

3.2.3 WorldExpo10数据集

文献[7]提出了包括199 923标签头在内的2010年世博会数据集。数据集中的所有图像都来自真实的世博场景。该数据集的3 980幅图像用于训练，其余图像分为5个场景，每个场景120幅图像用于测试。同时，该数据集还提供了ROI区域，因此实验中的所有训练和测试都是在ROI区域进行的。在训练过程中，由于数据集中的图像大小相同，该数据集中的裁剪大小就是图像的原始大小。

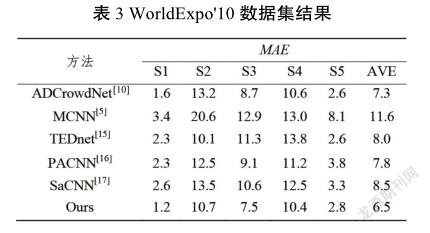
表3顯示了本模型算法和其他最近网络模型的对比结果，在5个测试场景中的3个场景中获得了最低MAE（越低越好），并且在所有5个场景中获得了最低的平均MAE。与第二排序法相比，该方法的MAE降低了0.8%。

3.2.4 UCF-QRNF數据集

这个包含1 535幅图像的数据集是由文献[20]提出的。该数据集中的1 201幅图像用于训练模型，其余图像用于测试模型。此数据集中的所有图像也来自互联网。与其他数据集相比，该数据集中的图像更为稠密，图像中的背景更接近实际场景，对网络应用具有更大的现实意义。如上所述，此数据集中的图像大小调整为1 024 pixel×768 pixel，以加快计算速度。在训练过程中，此数据集中的图像裁剪大小为512 pixel×512 pixel。

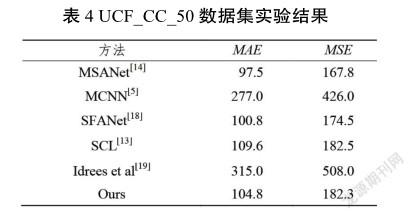
实验结果如表4所示，从表4可以看出，模型在这个数据集上并没有得到最好的结果，只得到了第三名，但是结果非常接近最优结果的值。与最佳网络相比，模型在MAE上高出7.3，在MSE上高出14.5。

3.3消融实验

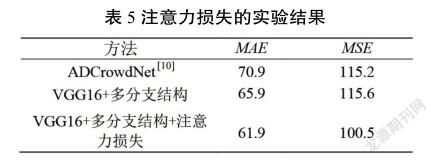
在这一部分中，注意力图损失的有效性在ShanghaiTech数据集上得到验证。在实验中，只使用VGG16主干和多分支结构来训练模型，因此损失函数没有注意力图损失，结果如表5所示。与最近的其他方法相比，无注意力图损失网络的结果在该数据集的性能上也取得了显著的进步。实验结果表明，注意力损失对结果有很大的影响。

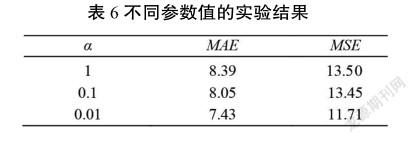
同时，还讨论了损失函数中不同参数对最终结果的影响。在ShanghaiTech PartB数据集上尝试了3个不同数量级的参数，结果如表6所示。当设置为0.01时，结果最好。

4结束语

针对人群计数问题，提出了一种新的基于卷积神经网络的模型来处理图像中人头尺度变化和背景噪声。该模型利用VGG16主干网不同阶段的多尺度特征生成密度图。在主干网络的多个阶段引入膨胀卷积，融合多尺度特征图，利用Sigmoid函数生成注意力图。利用多尺度的注意力图，模型可以更好地确定头部的位置，生成高质量的密度图。实验结果表明，该模型比现有的方法具有更好的性能。

在进一步的研究过程中，将考虑图像中存在的恶略自然天气和光照变化等环境因素，提高算法在实际环境中的鲁棒性。

参考文献

[1]钮嘉铭，杨宇.基于CNN的人群计数与密度估计研究综述[J].软件导刊， 2021， 20（8）：247-252.

[2]向飞宇，张秀伟.基于卷积神经网络的人群计数算法研究[J].计算机技术与发展， 2021， 31（7）：42-46.

[3] DOLLAR P， WOJEK C， SCHIELE B， et al. Pedestrian Detection： An Evaluation of the State of the Art[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2012， 34（4）：743-761.

[4] CHAN A B， VASCONCELOS N. Bayesian Poisson Regression for Crowd Counting[C]// 2019 IEEE 12th International Conference on Computer Vision. Kyoto： IEEE， 2009：545-551.

[5] ZHANG Y Y， ZHOU D S， CHEN S Q， et al. Single-image Crowd Counting via Multi-column Convolutional Neural Network[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas：IEEE， 2016：589-597.

[6] ZHANG L，SHI Z，CHENG M， et al. Nonlinear Regression via Deep Negative Correlation Learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2021， 43（3）： 982-998.

[7] ZHANG C， LI H S， WANG X G， et al. Cross-scene Crowd Counting via Deep Convolutional Neural Networks[C]// 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston： IEEE， 2015： 833-841.

[8] GUO D， LI K， ZHA Z J， et al. Dadnet： Dilated-attentiondeformable ConVent for Crowd Counting[C]// Proceedings of the 27th ACM International Conference on Multimedia. Nice： ACM， 2019：1823-1832.

[9] SAM D B， SURYA S， BABU R V. Switching Convolutional Neural Network for Crowd Counting[C]// 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu： IEEE， 2017： 5744-5752.

[10] LIU N，LONG Y，ZOU C， et al. ADCrowdNet： An Attention-injective Deformable Convolutional Network for Crowd Understanding[C]// 2019 IEEE Conference on Computer Vision and Pattern Recognition. Long Beach： IEEE， 2019： 3320-3229.

[11] CHEN X Y， BIN Y R， GAO C X， et al. Relevant Region Prediction for Crowd Counting[J]. Neurocomputing， 2020， 407： 399-408.

[12] WANG S Z， LU Y， ZHOU T F， et al. SCLNet： Spatial Context Learning Network for Congested Crowd Counting[J]. Neurocomputing， 2020， 404：227-239.

[13] WANG Y J， ZHANG W， LIU Y Y， et al. Multi-density Map Fusion Network for Crowd Counting[J]. Neurocomputing， 2020， 397：31-38.

[14] VARIOR R R， SHUAI B， TIGHE J， et al. Scale-aware Attention Network for Crowd Counting[J/OL]. （2019-01-17）[2022-10-13]. https：//arxiv.org/abs/1901.06026.

[15] JIANG X L， XIAO Z H， ZHANG B C， et al. Crowd Counting and Density Estimation by Trellis Encoder-Decoder Networks[C]// 2019 IEEE Conference on Computer Vision and Pattern Recognition. Long Beach： IEEE， 2019： 6126-6135.

[16] SHI M J， YANG Z H， XU C， et al. Revisiting Perspective Information for Efficient Crowd Counting[C]// 2019 IEEE Conference on Computer Vision and Pattern Recognition. Long Beach： IEEE， 2019：7271-7280.

[17] ZHANG L， SHI M J， CHEN Q B. Crowd Counting via Scale-adaptive Convolutional Neural Network[C]// IEEE Winter Conference on Applications of Computer Vision. Lake Tahoe： IEEE， 2018：1113-1121.

[18] ZHU L， ZHAO Z J， LU C， et al. Dual Path Multi-scale Fusion Networks with Attention for Crowd Counting[J/OL].（2019-02-04） [2022-10-13]. https：//arxiv.org/abs/1902.01115.

[19] IDREES H.， SALEEMI I. SEIBERT C， et al. Multi-source Multi-scale Counting in Extremely Dense Crowd Images[C] // 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland： IEEE， 2013：2547-2554.

[20] IDREES H， TAYYAB M， ATHREY K， et al. Composition Loss for Counting， Density Map Estimation and Localization in Dense Crowds[C]// European Conference on Computer Vision. Munich： Springer， 2018：544-559.