多阶段人口增长动力学模型分析

马春艳，李晓红，武力兵

（辽宁科技大学 理学院，辽宁 鞍山 114051）

我国是一个人口大国，自新中国成立以来，我国相继出台多项政策调控人口增长［1］。2020 年我国第七次人口普查结果显示，2020 年成为自新中国成立以来新生儿数量以及出生率最低的一年［2］。2021 年，国家出台三孩政策及相关生育配套支持措施［3］。

随着政策与经济、科学技术等带来的变化，人们的生育意愿逐渐变化［4］，为此，国内学者对人口生育率和生育意愿作了大量研究。陈卫［5］利用第七次人口普查数据分析国内生育政策对生育率的影响，发现女性婚育年龄的延迟具有压低生育率的作用。马芸芸［6］通过建立泊松回归模型得出结论，女性的生育意愿不仅受政策影响，城乡之间的生育意愿也存在较大的差别，同时住房、工作、经济压力会明显降低生育意愿。受教育程度越高，所在地区教育体系越完善，则越容易提高育龄人口的生育意愿。柳如眉等［7］利用时间序列数据进行多元回归分析，结果显示，生育率的变化与城乡收入水平变化呈正相关，育儿成本对城乡生育率的提高起负面作用。何兴邦［8］提到，跨地域农民工定居意愿的增加，即城市融入是导致农民工生育意愿下降的重要因素。蔡昉［9］指出，三胎政策的实行降低了“三育成本”（即生育、养育和教育的成本），从而对生育意愿的提升具有显著的正向影响。

随着生育意愿的逐年下降，预测人口总量对制定经济与资源配置相关政策、完善社会发展战略和建立社会保障体系等方面具有积极的参考意义［10-11］。人口预测有多种方法，如微分方程模型、灰色预测模型、线性时间序列模型、BP（Back propagation）神经网络预测模型、Logistic 增长模型、Malthus模型等［12］。由于人口发展过程是一个动态过程，可以用动力学方程描述。张娟等［13］通过建立人口动力学模型预测人口总量。Gurtin［14-15］在假定人口扩散的两种方式条件下，构建与年龄有关的人口扩散积分模型，并将人口扩散模型转化为偏微分方程组，得到了模型解存在的充分条件。Jäger 等［16］曾提出Boltzmann 型人口动力学方程，其中Boltzmann 方程含有碰撞算子，是分布函数所满足的一类微分方程。Arlottil 等［17-18］研究广义的Boltzmann 型人口动力学方程。Kang 等［19］研究具有非局部扩散和非局部边界条件的年龄结构种群模型的一些基本理论，应用Krasnoselskii不动点定理得到非平凡稳态的存在性，分析了平衡态的稳定性。Huo 等［20］研究一类年龄结构的反应扩散对流种群模型，考虑非线性死亡率和出生率，证明了系统稳态的存在性。Christoph等［21］针对含有非线性死亡和出生过程的年龄结构扩散种群模型，研究线性化稳定性原理。

人口发展一方面是自然选择，另一方面也受国家政策影响。国家政策直接影响生育意愿，但针对生育意愿对人口总量的定量研究成果较少。本文首先建立多阶段人口增长动力学模型，进而以此模型为约束条件，以实际数据与计算数据误差平方和为性能指标，建立最优控制模型，并利用粒子群算法结合全国1987～1999年人口数据确定模型中部分参数的最优解；其次利用2000～2020年的数据验证模型的可靠性，并通过误差分析总结生育率对人口总量的重要影响；最后在生育率中引入生育意愿参数，通过调整生育意愿参数，利用实际数据分析生育意愿对总人口增长趋势的影响。

1 人口增长动力学模型

为方便研究问题，本文根据人口增长实际特性，假设：各年龄段的转化率或成熟率在相当长的时间内视为常数；不考虑双胞胎及以上情况；不考虑国际迁移情况。

本文中所用参数符号及含义详见表1。

表1 本文所用参数符号及含义Tab.1 Symbol and meaning of parameters in this paper

1.1 人口增长动力学模型

设育龄人口各阶段人口数为Ni(i=1,2,3,4)，一旦生育就转移到下一个阶段，没有再生育的人口将其保留在本阶段，直至转移至老年人口阶段N5。不考虑生育双胞胎及以上等情况，模型中一位新生儿的降生伴随夫妻两位育龄人口转移至下一个阶段。图1 直观展示了各阶段人口之间的流动转化情况。

图1 各阶段之间人口转移图Fig.1 Population transfer diagram among each stages

基于上述假设和相关建模机理，得到如下人口增长动力学模型

其中，N0(t),…,N5(t)分别表示第t年儿童、各阶段育龄人口和老年人口，与等式右端N0,…,N5含义完全相同。将式（1）左端记N(t)=[N0(t),…,N5(t)]T，k=(k0,k1,k2.k3,k4)，则式（1）可写成如下向量形式

微分方程组（2）是线性微分方程组，满足微分方程解的存在唯一性定理。

定理1 微分方程组（2）存在连续依赖于初值和参数的唯一解。

1.2 人口增长动力学模型最优解

由于模型中各年龄段的转化率和成熟率k=(k0,k1,k2.k3,k4)无法通过统计数据获得，相关文献中也没有可参考的具体取值，本文以此为控制变量，以式（2）为约束条件，以各阶段实际与计算人口差的平方和为性能指标，得到最优控制模型（P）

式中：S0(t)、S1(t)、S2(t)分别为各年份实际儿童、育龄人口和老年人口。

定理2 最优控制模型（P）是一个线性二次型问题，有最优解。

各年份儿童人口N0、老年人口N5及儿童、老年人口的死亡率可通过统计年鉴查询，但无法查询到各阶段的育龄人口数据与死亡率。因此在计算时，假定在初始年份每个育龄阶段人口数相等，取为育龄总人口数据的平均值，即N1(0)=N2(0)=N3(0)=N4(0) ，各阶段育龄人口死亡率相同，即d1=d2=d3=d4。以1987 年为初始年，相关数据如表2 所示，其中生育率、死亡率等参数采用文献［13］中数据，均列于表2 中。考虑从1987 年到1999年共计13年的人口数据，即T=13。

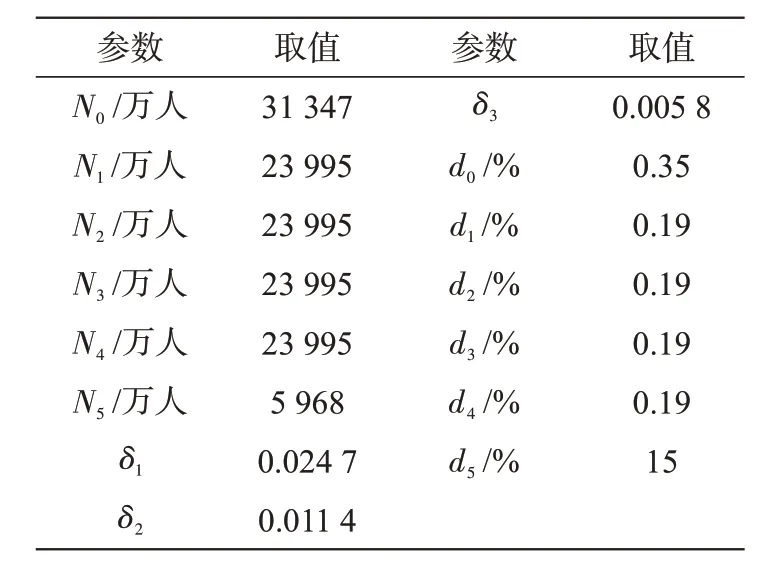
表2 1987年相关参数取值Tab.2 Related parameter values in 1987

采用粒子群算法，迭代100 次，计算得到适应值曲线，见图2。适应值在迭代65 次以后逐渐稳定，最优适应值为Jmin=1.139 8×109，最优参数k=［0.024 9，0.021 1，0.021 3，0.021 8，0.021 0］。因人口数值较大，且最优控制模型（P）的性能指标为平方和形式，故适应值较大。

图2 最优控制模型P的适应值曲线Fig.2 Adaptation value curve of optimal control model P

1.3 人口增长动力学模型验证与误差分析

1.3.1 人口增长动力学模型验证 选取2000年～2012 年各阶段人口数据进行模型验证。以2000年为初始年，相关参数来自文献［13］，详见表3。采用粒子群算法，计算2000～2012年人口总量的预测值及相对误差，详见图3。

表3 2000年相关参数取值Tab.3 Related parameter values in 2000

图3 2000年～2012年人口总量预测值及误差Fig.3 Errors and total population predicted values in 2000～2012

2000～2006 年的人口总量预测误差均小于0.1%，2007～2012 相对误差逐年变大。这与2006年国家实行单独二胎政策有关，从2007 年开始各阶段的生育率比2000 年有所提高，表明国家二胎政策有效提高了生育率。最大相对误差出现在2012年，为1.41%，这说明模型比较可靠。

1.3.2 人口增长动力学模型误差分析 为进一步探究国家政策对生育率的影响，继续对2013～2020年数据进行误差分析。

从2013年开始国家统计局公布各年龄段育龄人口数量，可以根据一胎、二胎及三胎新生儿数量计算各阶段育龄人口的生育率，如图4所示。

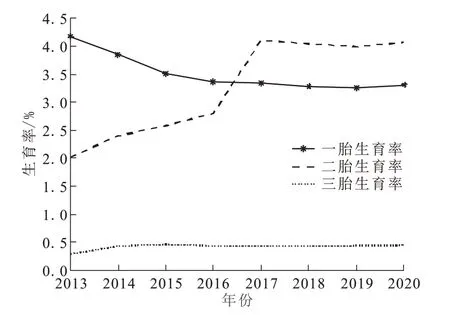
图4 2013年～2020年各阶段育龄人口生育率Fig.4 Fertility rate of population of childbearing age in 2013 ～2020

2013～2016 年、2017～2020 年各阶段育龄人口相应生育率均比较稳定，而在2017 年二胎生育率明显增加，且达到近年来最高。因此，本文将2013～2020 年分为两个阶段：2013～2016 年为单独二胎时期，2017～2020 年为全面放开二胎时期。以2013 年数据为初始值，详见表4，利用粒子群算法计算2013～2020年间的人口总量预测值及误差，结果如图5所示。

表4 2013年相关参数取值Tab.4 Related parameter values in 2013

图5 2013年～2020年人口总量预测值与误差Fig.5 Errors and total population predicted values in 2013～2020

人口预测最大相对误差0.247 68%，出现在2017年，低于2012年的最大误差1.41%，一方面说明模型可靠，同时也与2016 年国家全面开放二胎政策吻合。

现以2017 年数据为初始值，详见表5，计算2018～2020年人口总量及误差，结果见图6。

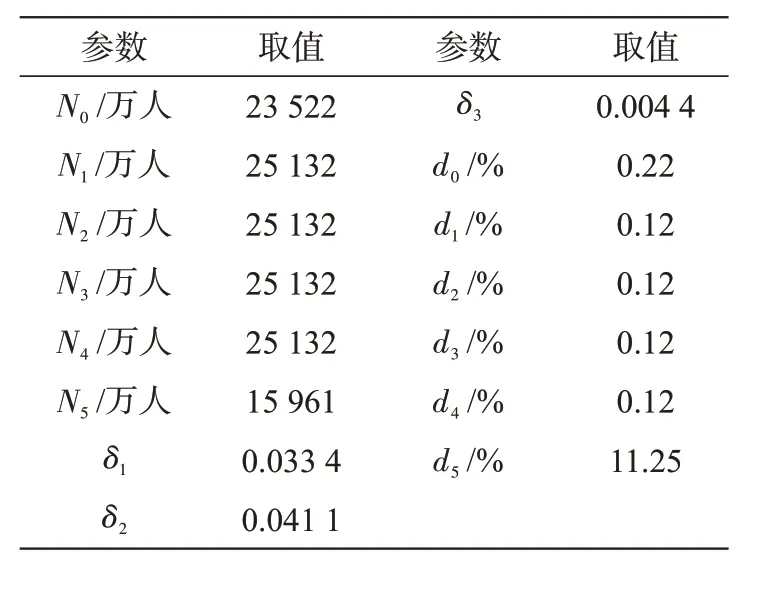
表5 2017年相关参数取值Tab.5 Related parameter values in 2017

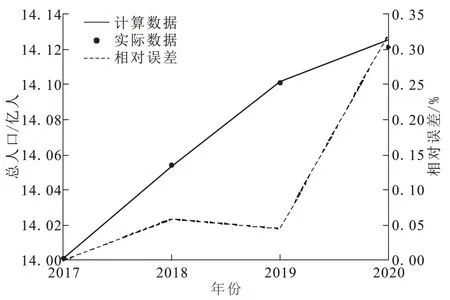
图6 2017年～2020年人口总量预测值与误差Fig.6 Errors and total population predicted values in 2017～2020

2017～2020 年间最高误差0.032%，均明显低于用2013 年和2000 年数据为初始值得到的误差。这表明生育率直接影响人口数量。

2 生育意愿对人口发展趋势的影响

2016 年国家全面放开二胎后，2017 年二胎生育率明显增加，之后稳中略有下降，而一胎生育率持续下降。不难看出，国家政策带动的是生育意愿，进而提高生育率。生育意愿在生育率中扮演着重要角色。本文将生育率看作自然生育率与生育意愿参数之积，分别讨论一胎、二胎、三胎生育意愿参数对人口总量的影响。

2.1 生育率的构成因素

自然生育率即为各阶段育龄人口生育的概率，将自然生育率记为λ=(λ1,λ2,λ3)，并假设其在各阶段生育时间间隔所表示的区间内服从正态分布。其中λ1表示15 岁到生育第一胎时间间隔的倒数，本文假定生育第一胎的年龄在18～30 岁之间，时间间隔为3～15年，因此λ1取值范围为［1/15，1/3］。λ2表示生育第一胎到生育第二胎的时间间隔的倒数，一般间隔时间通常为4～8 年，则λ2取值范围为［1/8，1/4］。λ3表示生育第二胎到生育第三胎及以上的时间间隔的倒数，一般间隔时间通常为2～5 年，则其取值范围为［1/5，1/2］。自然生育率在对应的范围内取随机数。

记生育意愿参数为μ=(μ1,μ2,μ3) ，分别表示一、二、三胎的生育意愿，在（0，1）之间取值。考虑到生育意愿完全是个人主观行为，因此对于生育意愿不做任何限制。由此，各阶段生育率

2.2 生育意愿对人口发展趋势的影响

为直观展示生育意愿参数对人口总量的影响，本文以2020年的数据（表6）为式（2）的初始值，通过调整各阶段生育意愿参数，计算未来人口数量，预测人口发展趋势。通过比较不同参数下人口发展趋势，确定生育意愿参数对人口发展的影响。

表6 2020年参数取值Tab.6 Related parameter values in 2020

首先采用2020 年的生育率，利用式（4）计算2020 年各阶段人口生育意愿参数，结果详见表7。通过模型（2）得到未来一些年份人口总量，如图7所示。

表7 2020年生育率参数Tab.7 Fertility rate parameters in 2020

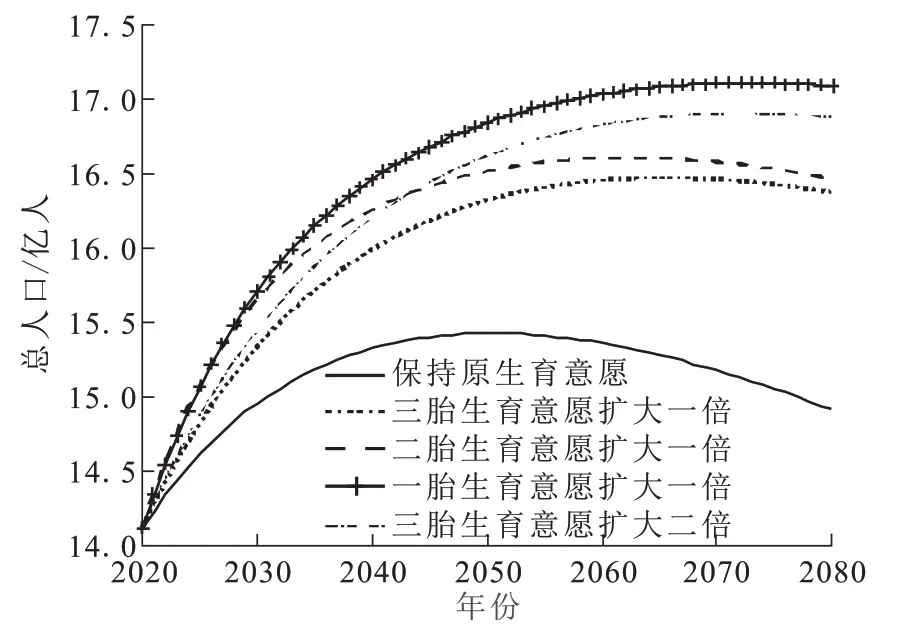
图7 调整生育意愿后人口发展曲线Fig.7 Population growth curve after adjusting fertility intention

按照2020 年的生育率，预计在2050 年人口总数达到峰值，之后逐步走低。很多专家已意识到这个问题，国家也出台了全面开放三胎的生育政策。

下面分别将一、二、三胎生育意愿参数扩大1倍，三胎生育意愿扩大2 倍，在这四种情况下计算人口总量，并绘制人口发展曲线，如图7 所示。将生育意愿调整后的人口峰值及年份列于表8中。

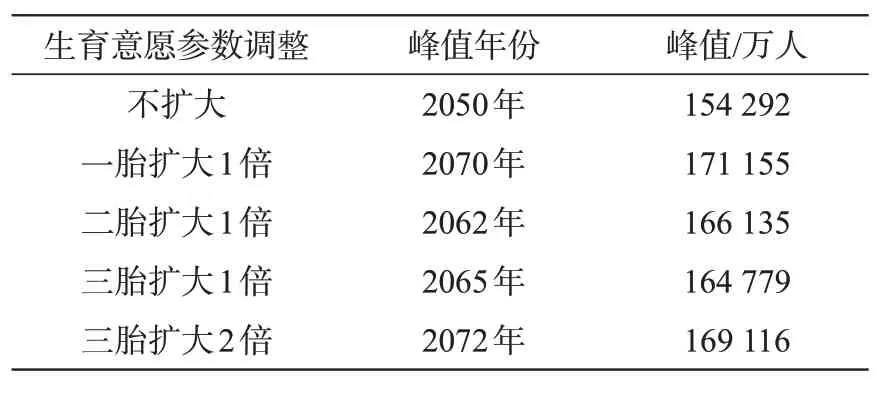
表8 调整生育意愿后人口峰值比较Tab.8 Comparison of population peak after adjusting fertility intention

与采用2020 年生育率相比，提高各阶段生育意愿后，人口总量均有显著提升，人口峰值到达的时间延后5～20年。而且，扩大一胎生育意愿对人口的效果明显优于扩大二、三胎生育意愿的情形，不仅延迟了到达人口峰值的时间，人口峰值也达到了更高的水平。同时还可以发现，一胎生育意愿参数扩大1倍与三胎生育意愿参数扩大2倍，人口峰值到达的时间均在2070 年左右，而一胎生育意愿参数扩大1倍预测的人口峰值更高。因此，在提高人口数量，遏制人口出生率持续走低的工作中，重点在于提升一胎生育意愿，可以达到事半功倍的效果。

3 结 论

本文建立多阶段人口增长动力学模型，估计各阶段之间的转化率，采用误差分析验证模型正确性的同时，也表明生育率对人口总量的巨大影响，展示了国家政策对生育率的直接影响。在生育率中引入生育意愿参数，分别调整生育意愿，预测人口未来发展趋势。提升一胎、二胎、三胎生育意愿，均可显著提升人口总量，不同程度地延后人口峰值到达的时间；提升一胎生育意愿的效果明显优于提升二、三胎生育意愿效果。