调频加网对于全息再现图像的影响

解文博，王庆

调频加网对于全息再现图像的影响

解文博，王庆

（齐鲁工业大学，济南 250353）

对全息图进行加网处理，实现计算全息图的二值化，将计算全息图应用于印刷领域。本文设计计算全息图进行调频加网的整体方案，讨论不同的加网算法对计算全息再现图像的质量影响。首先，对3幅不同类型的灰度图片进行计算全息编码得到全息图；然后利用误差扩散算法和抖动算法对全息图进行调频加网获得二值化全息图；之后通过光场重建得到全息再现图像。对全息再现图像进行峰值信噪比和结构相似性数据比较发现，误差扩散算法更适用于计算全息二值化处理，抖动加网使计算全息图产生周期性图案，导致再现全息图产生混频现象，全息再现图像的质量下降。加网导致全息图再现质量下降，误差扩散算法可以得到较好的再现像，适用于全息图的二值化处理；与此同时，抖动算法会产生混频现象，因此抖动算法并不适用于全息图二值化处理。

计算全息；相位恢复算法；数字加网；误差扩散算法；抖动算法

随着图像处理、桌面排版、广告、装潢设计等领域对输出图像质量的要求日益提升，图像处理的技术伴随着新时代计算机的发展而不断的升级更新，与此同时印刷输出的图像也随之更加逼真。因为全息图像同时记录了振幅和相位信息，所以全息技术再现出的图像更加生动，具备了物体所有光学信息，为再现三维立体图像提供了前提条件。随着计算机技术和微电子技术迅速发展，给计算全息术的发展创造了条件。全息成像技术是盖伯（Gabor）在1948年提出[1]，之后，激光技术的成熟，彻底解决了普通照明再现全息技术时间和空间相干性差的这一实际应用难题。1965年，Kozma等[2]首次制作出了第1张计算全息图，计算全息技术有效摆脱了光学全息技术硬件要求较高的壁垒，为全息技术的理论研究创造了条件。计算全息的主要特点是可以灵活地进行编码，以再现一个物体的全息图像。因此，后来出现了许多编码方法，如罗曼编码、四阶迂回相位编码、三阶迂回相位编码等，为计算全息的发展奠定了基础。1967年Lohmann等[3]首次将快速傅里叶变换（简称FFT）应用到计算全息中，使得计算速度迅速加快，为计算全息的普及奠定了基础。近年来，科研工作者们对计算全息的编码有了更加深入的研究，将GS算法、误差扩散算法、深度学习等方法引入计算全息技术中，使计算全息再现图像的速度更快并且再现图像的质量更佳[4-6]。由于计算全息编码的不断优化，计算全息技术逐渐成熟，使得计算全息技术在很多领域得到了应用，如动态计算全息术、彩色全息术、计算全息术运算技术、计算全息图数字再现及制作、计算全息光学加密技术、计算全息编码技术、计算全息三维显示技术等方面[7-9]。

计算全息再现图像依据其全光学信息载体的优势，必将成为未来数字图像的主要载体。虽然全息技术在众多领域得到应用，但计算全息技术在印刷领域的应用相对较少。有研究学者利用全息编码实现防伪印刷，而以全息图作为原稿实现加网印刷的研究几乎空白。全息图的印刷实现首先需要解决的是图像的二值化问题。众所周知，印刷图像是通过网点来再现图像的，而目前印刷图像的网点实现主要通过照排机或直接制版机（Computer to Plate, CTP）在胶片或印版进行二值化激光曝光完成。二值化曝光实现印刷用网点可分为调幅网点和调频网点两大类。其中，调频加网主要的方法有抖动法、误差扩散法、迭代法等[10-11]。因此，计算全息图的加网即计算全息图的二值化处理。本文将计算全息图实现调频加网后，对所生成的网点全息图进行全息再现，旨在模拟加网方式对全息图印刷再现后的图像质量影响，探讨全息图印刷的理论可行性。

1 全息再现图像的加网计算

1.1 加网全息图再现实验方案

本文旨在研究计算全息图在印刷中的应用问题，设计了全息图的加网实验，并利用加网后的全息图进行原图像再现，最终利用信噪比等客观图像评价参数对计算全息图在加网后的图像质量进行评价。本次实验分为3个阶段：计算全息图的生成、计算全息图的加网、加网全息图的再现以及相应的质量评价。具体流程如图1所示，第1阶段计算全息图制作过程分为三部分：首先，对原稿进行离散化采样；其次，根据菲涅耳衍射理论计算原稿光波以及参考光波到达记录单元（Charge-Coupled Device，CCD）的物光波复振幅分布；最后，通过全息编码模拟振幅型计算全息图在CCD上的复振幅分布，该复振幅分布为原稿的全息干涉条纹图而非原稿本身。第2阶段为全息图的加网过程，本文采用4种误差扩散法和3种抖动法进行调频加网。第3阶段为加网全息图的再现过程，将加网后的全息图利用一次快速傅里叶（1–FFT）重建，以及虚拟数字全息图和四次傅里叶运算（Virtual Digital Hologram 4FFT，VDH4FFT）模拟干涉条纹全息图对原稿的再现效果[12]；然后对再现效果进行客观质量评价，从而探讨调频加网对全息再现图像的影响。

1.2 全息图制作

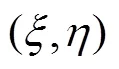
图1 实验流程

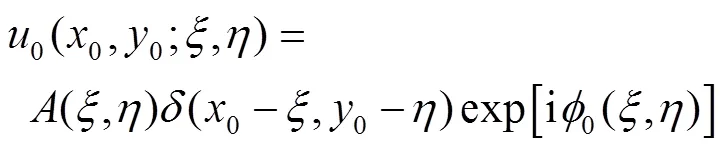
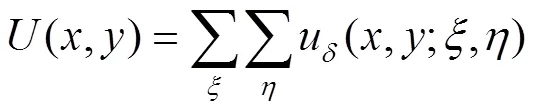
根据全息衍射理论，假设参考光波为均匀的球面波且参考光位于(,, −r)，则参考光波的复振幅为：

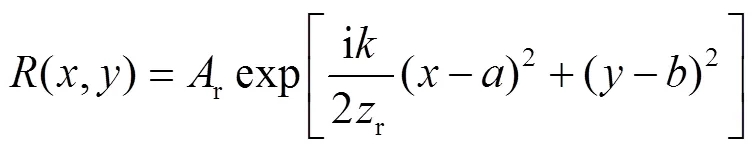
式中：A为参考光振幅，将物光与参考光干涉得到CCD平面上的干涉场强度为：

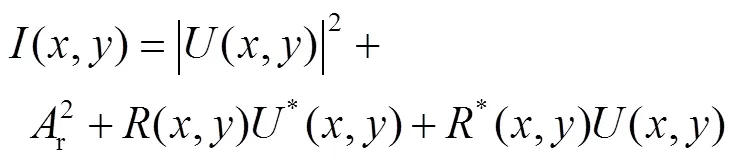
根据式（1）—（5）设置本实验所用的相关参数：波长=532 nm；衍射距离0=1 000 mm；取样数=1 024并且本文采用的实验原稿来自于数字图像库Image Processing Place和USC–SIPI，具体图像如图2中a、b、c所示。所选图像分别代表不同场景，且图片线条清晰。由于1–FFT重建光场图需要被二次重建，为了便于二次重建时选择二次重建图像的中心，分别将3幅实验原稿图像的中心用黑点做标注，其中图2c为彩色图像，实验前转换成灰度图像。具体模拟计算步骤如下：首先，对3幅实验原稿进行一次快速傅里叶变换及快速卷积算法（S–FFT算法）[14]，从而得到物光场到达CCD的复振幅；之后，通过物光场到达CCD的复振幅与参考光的复振幅相加，并且进行全息编码得到计算全息图，具体如图2d、e、f所示。

图2中的d、e、f为计算全息图，计算全息图上的干涉条纹模拟记录了图片上的相位和振幅信息，该干涉条纹在肉眼条件下并不能判定图像特征，因此图像质量只能通过全息图再现后进行评价。

1.3 全息图的加网

本文使用调频加网中的4种不同的误差扩散算法（Stucki、Burkes、Floyd–Steinberg、Jarris–Judice–Ninke（JJN））和3种不同的抖动算法（Bayer、Halftone、Screw）分别对3幅计算全息图进行加网[15]。所得结果如图3所示。

图2 实验图像及其计算全息图

图3 调频加网计算全息图

图3中每行代表不同类型图片的加网全息图，每列代表不同的调频加网算法，并且每张计算全息图的左下角为其放大图。由于全息干涉条纹图借助人眼很难观察出图像内有用信息，因此对比加网前后的计算全息图很难察觉出具体变化。但从图3中还是可以很明显地发现经过误差扩散法和抖动法加网后的计算全息干涉条纹图具有明显的差异，即经3种抖动法加网后计算全息图具有明显的周期性图案，这种周期性变化是因为抖动矩阵一般用8×8的矩阵，当其中的矩阵对应像素计算结束后，下一个矩阵中的像素会按照相同的抖动矩阵继续计算。经4种误差扩散法加网后计算全息图并没有表现出明显的周期性图案，这是因为误差扩散法是通过滤波器将每个点的误差扩散到其他相邻像素点上，因此加网后图像不会产生明显的周期性变化。综上发现，加网过程造成了干涉全息图的图文变化，因此必定会影响再现后的图像质量，而加网导致全息图像产生周期性图案的现象会对后续全息图再现产生更加严重的影响。

1.4 加网全息图的再现

在1–FFT的光场重建平面上选择需要再现的图像，通过衍射逆运算得到与重建图像的物理尺寸相同的模拟数字全息图，运用角谱衍射理论计算得到到达像平面的衍射场，之后得到二次重建后的计算全息再现图像，如图5所示。从图5中可以看出，非加网再现图较原图有明显的质量差别，这是因为计算全息系统不能充分地记录物光场的高频信息，所以再现图像比原图像的质量差。其次，每张加网后重建的图像上都有不同程度的散斑结构，这是因为计算全息图是将物体表面视为非光学光滑的散射面做出的。误差扩散法和抖动法对再现图像的质量表现出明显差别。3种抖动算法的二次重建像依然可以看到有零级像，因此，传统的抖动法在全息图的二值化过程中并不适用。对4种误差扩散法而言，二次重建像没有零级像干扰，很好地实现再现像分离，适用于全息图的二值化。Floyd–Steinbery的二次重建像质量效果最差，图像边缘再现不清晰，这可能是因为Floyd–Steinbery算法所用到的滤波器的构造比较简单。Stucki、Burkes、JJN算法的滤波器在传统滤波器上进行改进，将1个像素点上的误差扩散到更多的像素点上，因此再现图像质量较好，图像边缘更清晰，可以实现全息图的二值化处理。综上发现，加网确实对全息再现质量产生明显影响。本文所用的误差扩散算法适用于全息图的二值化处理，不同误差扩散算法对计算全息再现像的影响不同，而传统抖动法由于产生的周期性图案而造成再现图像的混频现象，无法应用于全息图的二值化。

图4 调频加网计算全息图1–FFT重建

2 加网全息再现图质量评价

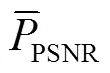
表1 调频加网全息再现图的质量评价参数

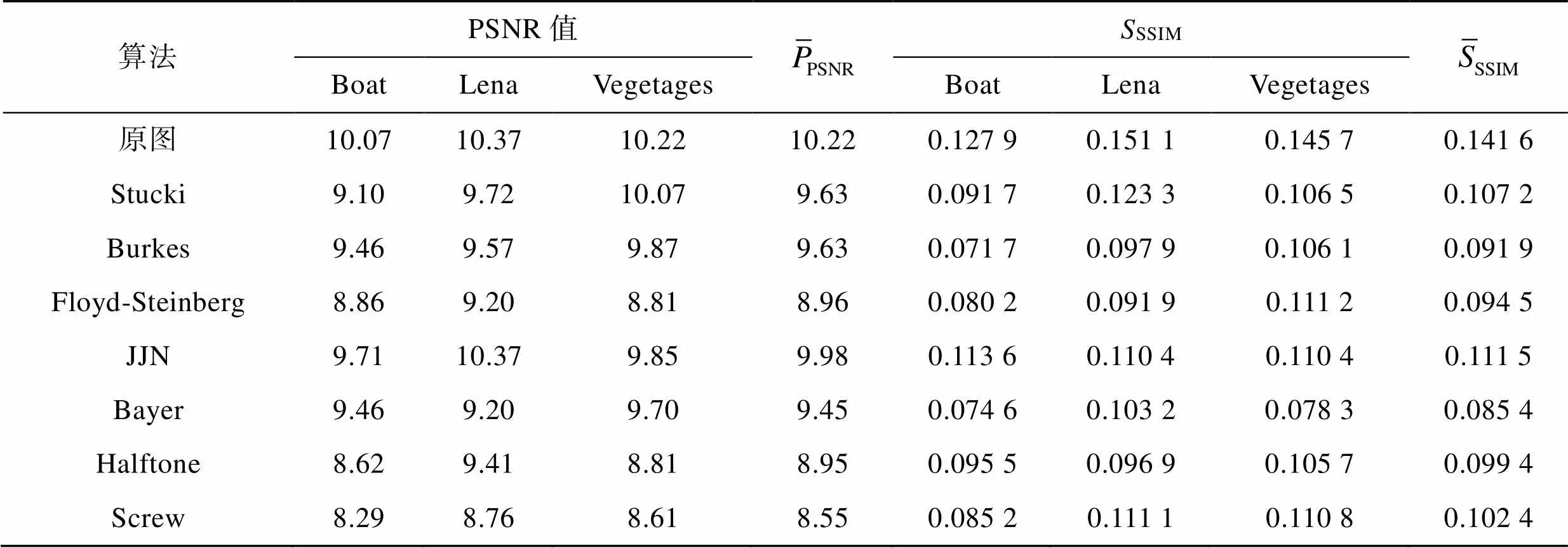
Tab.1 Quality evaluation parameters of FM screened holographic reproduction images

3 结语

计算全息技术记录物体的相位和振幅信息，可以完整地再现原始物体，是一种真正的三维显示技术，并且计算全息技术的灵活性和可重复性具有广泛的应用前景。若要将全息图应用在印刷领域中，则必须要对全息图进行数字加网处理，使其成为二值化全息图。本文旨在研究全息图二值化后再现图像的可行性以及各类调频加网对全息再现后图像质量的影响。本次实验结果表明，在传统调频加网方法中，因为误差扩散法实现全息图二值化过程中不产生明显的周期性图案，所以可模拟出原稿影像，而抖动法使图像产生明显的周期图案，产生混频，全息再现失败。并且，本次实验中的全部加网算法对全息再现质量影响较为明显，新技术的开发可为计算全息图在印刷领域的应用提供更为可靠的理论依据。

[1] GABOR D. A New Microscopic Principle[J]. Nature, 1948, 161(4098): 777.

[2] KOZMA A, KELLY D L. Spatial Filtering for Detection of Signals Submerged in Noise[J]. Applied Optics, 1965, 4(4): 465-73.

[3] LOHMANN A W, PARIS D P. Binary Fraunhofer Holograms, Generated by Computer[J]. Applied Optics, 1967, 6(10): 1739-1749.

[4] REN Z, SO K H, LAM E Y. Fringe Pattern Improvement and Super-Resolution Using Deep Learning in Digital Holography[J]. IEEE Transactions on Industrial Informatics, 2019, 11(15): 1-9.

[5] JIAO S, ZHANG D, ZHANG C, et al. Complex-Amplitude Holographic Projection with a Digital Micromirror Device (DMD) and Error Diffusion Algorithm[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2020, 26(5): 1-8.

[6] ISHII Y, SHIMOBABA T, BLINDER D, et al. Optimization of Phase-Only Holograms Calculated with Scaled Diffraction Calculation through Deep Neural Networks[J]. Applied Physics B, 2022, 128(2): 1-11.

[7] 王晓蓉. 计算全息技术应用及其发展趋势综述[J]. 激光杂志, 2016, 37(6): 20-24.

WANG Xiao-rong. Overview for the Application and Development Tendency of Computer Generated Holography[J]. Laser Journal, 2016, 37(6): 20-24.

[8] BELAID S, HATTAY J, MACHHOUT M. A New Concept for Lossless Compression and Transmission of Inline Digital Holograms[J]. Tele-Holography, 2022, 1: 3.

[9] SHI Liang, LI Bei-chen, KIM C, et al. Towards Real-Time Photorealistic 3D Holography with Deep Neural Networks[J]. Nature, 2021, 591(7849): 234-239.

[10] 王海文, 李杰, 万晓霞, 等. 多光谱打印的变频调幅加网设计方案研究[J]. 光学技术, 2016, 42(3): 220-224.

WANG Hai-wen, LI Jie, WAN Xiao-xia, et al. Design Plan Research of Variable Frequency Amplitude Modulation Screening for Multispectral Printing[J]. Optical Technique, 2016, 42(3): 220-224.

[11] 韩雪莹, 王琪, 葛乃馨. 基于调频的相位调制潜像防伪方法[J]. 光学学报, 2019, 39(8): 0805001.

HAN Xue-ying, WANG Qi, GE Nai-xin. Anti-Counterfeiting Method of Phase-Modulated Latent Images Based on Frequency Modulation[J]. Acta Optica Sinica, 2019, 39(8): 0805001.

[12] 吴湾. 数字全息波前重建算法研究[D].武汉: 武汉纺织大学, 2020: 30-48.

WU Wan. Research on Digital Holographic Wavefront Reconstruction Algorithm[D]. Wuhan: Wuhan Textile University, 2020: 30-48.

[13] 戚康男, 秦克城. 统计光学导论[M]. 天津: 南开大学出版社, 1987: 207-257.

QI Kang-nan, QIN Ke-cheng. Introduction to Statistical Optics[M]. Tianjin: Nankai University Press, 1987: 207-257.

[14] 李俊昌, 宋庆和, PICART Pascal, 等. 离轴数字全息波前重建算法讨论[J]. 中国激光, 2014, 41(2): 81-89.

LI Jun-chang, SONG Qing-he, PASCAL P, et al. Discussion of Wavefront Reconstruction Algorithm of Off-Axis Digital Holography[J]. Chinese Journal of Lasers, 2014, 41(2): 81-89.

[15] 何可丁. 误差扩散法数字加网的优化与分析[D].济南: 齐鲁工业大学, 2021: 15-26.

HE Ke-ding. Optimization and Analysis of Error Diffusion Method for Digital Addition Network[D]. Jinan: Qilu University of Technology, 2021: 15-26.

[16] HORÉ A, ZIOU D. Image Quality Metrics: PSNR vs. SSIM; Proceedings of the 20th International Conference on Pattern Recognition[C]// ICPR 2010, Istanbul, Turkey, 2010.

Effect of Frequency Modulation Screening on Quality of Holographic Reproduction Image

XIE Wen-bo, WANG Qing

(Qilu University of Technology, Jinan 250353, China)

The work aims to screen the hologram to realize the binarization of the computational hologram and apply the computational hologram to the printing field. An overall scheme of frequency modulation screening for computational hologram was designed and the effects of different screening algorithms on the quality of holographic reproduction image were discussed. Firstly, three types of grayscale images were holographically encoded to obtain holograms and then these holograms were subject to frequency modulation screening to gain binarized holograms by the error diffusion and dithering algorithms. Finally, the binarized holograms were transformed holographic reproduction images by means of light field. According to the comparison between the peak signal-to-noise ratio (PSNR) and the structure similarity index measure (SSIM) data of holographic reproduction images, the error diffusion algorithm was more suitable for computing holographic binarization and the dithering screening caused periodic patterns on the holograms, which resulted in frequency mixing phenomena on the holographic reproduction images,so the quality of the holographic reproduction images was reduced. Screening degrades the quality of holographic reproduction images. The error diffusion algorithm has better reproduction images and is suitable for hologram binarization. Furthermore, the dithering algorithm produces frequency mixing, so it is not suitable for hologram binarization.

computational holography; phase recovery algorithm; digital screening; error diffusion algorithm; dithering algorithm

TS801.8

A

1001-3563(2023)09-0282-07

10.19554/j.cnki.1001-3563.2023.09.034

2022−06−03

解文博（1998—），女，硕士生，主攻轻工技术与工程。

王庆（1978—），男，博士，副教授，主要研究方向色彩学。

责任编辑：曾钰婵