地震动强度参数相关性对地震滑坡危险性影响分析
2023-05-12刘同同杨玉萍李朝阳
刘同同,杨玉萍,李朝阳,程 印
(1.西南交通大学 土木工程学院,四川 成都 610031;2.四川省公路规划勘察设计研究院有限公司,四川 成都 610041)
0 引言
几十年以来,多起滑坡事件证明地震引起的滑坡是最具影响的地震灾害之一。例如,在2008年汶川地震期间,15000起地震引发的滑坡、落石和泥石流事件使死亡人数增加了2000人[1]。在众多的滑坡评估方法中,通常使用Newmark位移预测模型来预测可能发生的滑坡位移。Newmark位移预测模型是NEWMARK[2]于1965年首次提出的基于均值地震动强度参数(IMs)的预测模型,随着 GIS技术的不断创新和发展,该方法被国内外学者大量的应用于地震滑坡危险性评估研究中[3-8]。IMs的相关性在空间分布的基础设施系统的地震灾害分析中很重要[9]。例如,评估建筑组合的风险通常需要多个周期的谱加速度(SA)场[10],还需要考虑IMs的相关性。研究证实:IMs的相关性对地震损失估计的影响可能是显著的,特别是对总体损失估计的不确定性程度而言[9,11]。对于地震滑坡而言,考虑IMs的相关性也是非常有必要的。然而,在地震滑坡危险性评估中,多采用IMs的均值预测滑坡永久位移,其不确定性中的相关性往往被忽略,将会导致出现不真实的地震动特征,最终可能造成预测结果与实际结果相差甚远。
近年来,各种预测滑坡位移经验模型已建议将IMs和Newmark累积位移模型联系起来[12-15]。其中:峰值地面速度(PGA)、峰值地面加速度(PGA)和阿里亚斯强度(Ia)等常用IMs的均值作为模型输入,用于评估区域分布的地震边坡稳定性[16-17]。SAYGILI等[13]利用传统非线性拟合方法,将IMs作为输入参数预测滑坡永久位移;WANG等[15]利用在非参数方式处理综合数据集方面通常具有优越能力的机器学习方法(XGBoost),提出一种基于多地震动参数的机器学习框架预测滑坡永久位移。然而,现有的Newmark永久位移模型将IMs均值作为输入,并不能很好地准确预测位移以及评估地震滑坡危险性。为了更加准确的预测和评估,需要考虑IMs输入的随机性和不确定性。在这过程中,对IMs的相关性的考虑至关重要。因此,有必要研究IMs相关性特征对地震滑坡危险性分析结果的影响,以及在不同工况和因素下影响的差异和变化规律。
本文将基于Newmark永久位移算法,利用全概率地震滑坡危险性分析方法,研究在不同临界屈服加速度ac、永久位移模型、场地条件和断层距情况下,是否考虑IMs对地震滑坡危险性结果的影响大小和变化规律,为合理进行滑坡防护提供理论依据和参考。
1 全概率地震滑坡危险性分析
本文根据刘甲美等[7]和李雪婧等[18]对临界加速度的选取原则,选取三种不同的临界屈服加速度ac,分别为:0.02、0.1和0.3 g,反映边坡的地震滑坡易发程度从大到小;选取3种永久位移模型,分别为:2种传统Newmark位移预测模型和1种基于机器学习的Newmark位移预测模型;美国NEHRP(National Earthquake Hazards Reduction Program)规范中,根据VS30(地表下30 m内土层的平均剪切波速度)范围对场地进行了分类,该分类方法在世界范围内被广泛应用。SEYHAN等[19]根据该场地类别分类的VS30范围以及NGA-West2数据库中实测VS30值,提出了各类场地类别的VS30代表值。本文采用了该代表值研究三类场地类别的影响,分别是:VS30=913(m/s)(B类场地)、VS30=489(m/s)(C类场地)和VS30=266(m/s)(D类场地);同时选取3种断层距,分别是10、30和60 km,代表近中远三种不同场地距离。分析对比IMs相关性在上述不同因素下对地震滑坡危险性结果的影响。
全概率地震滑坡位移危险性分析旨在绘制滑坡永久位移危险曲线,而非某个指定危险地面运动水平估算单一位移值[13]。与地震动强度危险性水平类似,滑坡永久位移年超越率曲线对应不同的危险性水平,将地面运动危险曲线与位移预测模型及其给定ac值的变化进行卷积来计算:
(1)
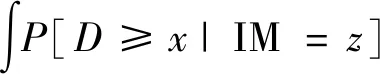
当涉及更复杂的因素,如多种地震动衰减关系、复合地震活动模型以及多参数的不确定性时,由于无法直接进行解析表达,更复杂和全面的分析方法将会受到限制。使用蒙特卡罗模拟(Monte Carlo)实际的概率分布来拟合每个具有不确定性的变量,产生一系列的合成地震事件可以直观体现由于地震发生导致的灾害情况。
蒙特卡罗方法也称统计模拟方法,基于概率与统计理论,通过随机数或伪随机数使用电子计算机来进行随机模拟或抽样,以此来获取问题近似解[20]。每次随机试验结果都可能有所区别,但当试验次数趋向于无穷时,估计值无限趋向于真实值。
基于公式(1),该研究采用蒙特卡罗模拟的方法计算概率滑坡危险性,其步骤如下:确定模拟次数和模拟的统计周期;通过进行蒙特卡罗模拟地震发生的泊松过程,确定地震发生的震级和断层距从而形成地震目录;通过地震动预测方程(GMPEs)计算不同地震场景的IMs预测均值;考虑IMs相关性对残差进行修正,模拟出具有相关特征的抽样残差;计算均值和残差之和,得到具有相关性的IMs;将计算出的IMs带入滑坡永久位移预测模型,计算具有随机性的地震滑坡永久位移值D,通过下式求出滑坡永久位移D超过特定位移值x的年平均超越率:
(2)
不同的超越率对应不同的危险性水平,可针对具体边坡情况得到相对应的滑坡风险位移值来进行设计指导工作。以下第2和3节将介绍生成地震目录的具体实现方法和过程。
2 地震目录生成
地震目录是地震活动性研究和地震危险性分析最为重要的资料。本文进行地震目录生成时,为简化计算,仅考虑由断层产生的地震,并通过模拟产生地震的数量、震级大小和震源位置来确定地震目录。
2.1 地震数量生成
假设地震的发生遵循泊松分布,在[0,t]这段时间内,发生k次m0级以上的地震的概率为[21]:
(3)
式中:v0为m0级以上地震的年平均发生率。对上式进行求和,得到地震发生(次数大于等于1次)的概率分布函数为:
(4)
对上式进行随机抽取一个[0,1]之间的随机数,作为概率分布函数值,再根据给定年发生率和时间t,就完成一次该时段地震发生k次的模拟,重复这样的过程最终能得到指定年限内的地震数量。
2.2 震级大小的生成
模拟产生的震级大小由震级-频度关系决定。震级-频度关系是指某个地区地震时间发生的次数(频率)与地震震级之间的关系。假设N为某地区某段时间内发生地震事件震级大于等于m的次数,则N与m之间近似存在对数线性关系:
lgN(m)=a-bm(m0≤m≤mu)
(5)
式中:a和b分别为反映地震活动水平和大小地震比例关系的常数。b值的选取取决于该地区介质强度与地应力大小,地应力高的地区,b值也高,反之亦然。m0为震级下限,通常取4~4.75;mu为震级上限。在本文中选取矩震级上限为8,矩震级下限为4。根据式(5),地震事件的震级分布可以转换为指数分布:
N(m)=eα-βm
(6)
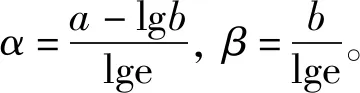
(7)
其概率密度函数为:
(8)
2.3 震源的确定
地震的发生是一个能量释放的过程,不同面积的断层破裂释放能量大小与发生地震事件的震级大小有关。假设地震发生时,断层破裂面积为矩形,且矩形质心在断层平面位置上服从均匀分布,通过断层破裂面积与地震震级的经验关系即可确立地震的震源。断层破裂优先满足断层宽度,再计算破裂长度。其中:走滑断层破裂面积与震级关系如下:
lg(A)=0.9MW-3.42
(9)
式中:MW为矩震级,A为走滑断层破裂面积。
郭增建等[22]提出了由构造分段求震级的方法,建立了震级与断层长度的关系式:
Ms=3.3+2.1lgL
(10)
式中:Ms为面波震级,L为地表破裂长度。
面波震级和矩震级转换通过以下公式计算:
MW=0.844MS+0.951
(11)
采用式(10)-式(11),使用2.2节所得到的矩震级MW通过转换为面波震级MS,计算断层破裂长度L值。若发生Ms=8.0级地震,则地表破裂长度为173 km。参考上述值,本文假设某一的走滑断层倾角为90°,总长度为170 km,断层外有三个边坡场地,与断层的垂直距离分别为10、30和60 km,如图1所示。考虑近远断层距离对滑坡地震风险的影响,故设置三个断层距位置来进行研究。同时考虑不同场地类别对滑坡风险的影响。
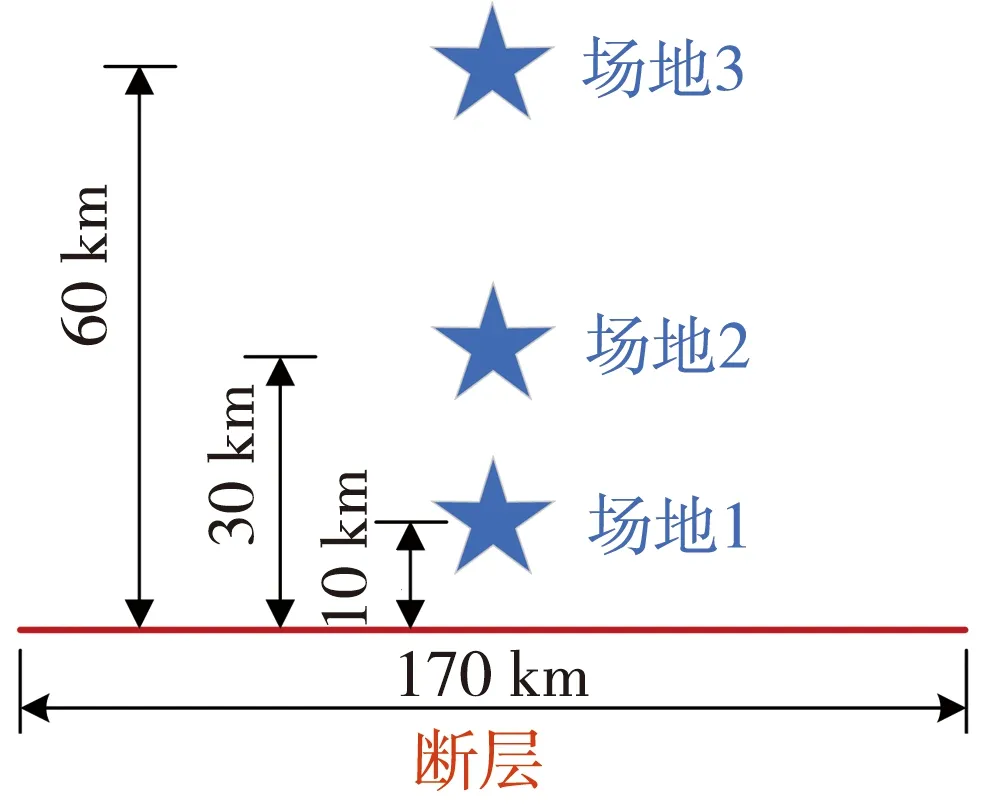
图1 断层与边坡示意图Fig. 1 Schematic diagram of the fault and slopes
3 地震目录生成结果
采用蒙特卡罗进行地震模拟,对其进行周期为100 a,次数为50 000次的地震模拟,一共产生1 732 809次Mw=4.0级以上地震,其震级与断层距分布见图2。由图2可得:对于三个断层距场地,频度最高的断层距分别位于30~35 km、40~50 km和60~70 km。由于假设整条断层中发生地震时,破裂中心点位置服从均匀分布,断层距为10 km时与断层的垂直距离与断层长度相比相差很大,同时发生地震时的大多数震级为断层破裂长度并不长的小震级,所以对于近场而言,实际频度最高的断层距并不是10 km以内。随着场地与断层垂直距离的增加,频度最高的断层距区间也向着垂直距离靠近。

图2 震级与震距(断层距Rrup)分布图Fig. 2 Distribution of magnitude and distance
如图3所示,从模拟出的地震事件中筛选出震级(Mw)大于6.5级的事件,可以看出对于三个断层距而言大震级事件的断层距频次最高的分别是10、30和60 km,与场地到断层的垂直距离相符合。
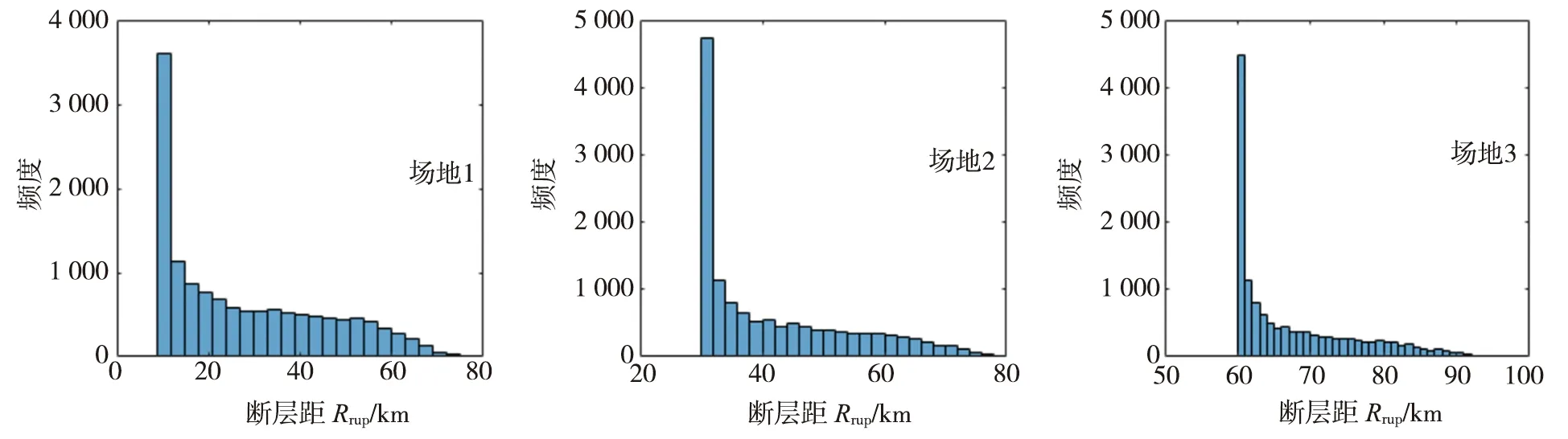
图3 三个断层距Mw>6.5的断层距分布Fig. 3 Rupture distance distribution of three epicenters with Mw>6.5
4 Newmark位移预测模型
本文通过选取传统方法非线性拟合得到的Newmark位移预测模型和基于机器学习的Newmark位移预测模型,探究IMs相关性对基于两种不同类型预测模型的危险性结果的影响差异。
4.1 传统的Newmark位移预测模型
由于SAYGILI等[13]模型(简称“SR08模型”)在预测Newmark位移时考虑了相同的预测变量方面很受欢迎,因此我们以SR08模型作为传统模型的代表。SR08 (PGA,PGV,Ia)模型表达公式如下:

(12)
(13)
式中:D=Newmark位移(cm);PGA、PGV、Ia和ac的单位分别是g、cm/s、m/s和g。
为了进行比较,本文采用 WANG等[15]根据最新的NGA-West2数据对SR08模型更新之后的模型。在之后本文中称“SR08_up模型”,表达形式如下:
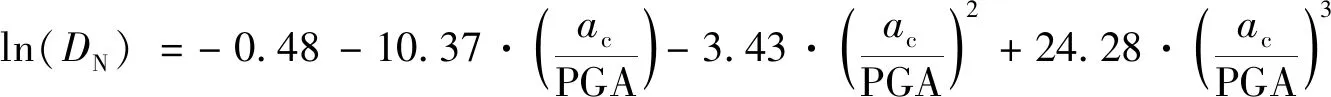
(14)
(15)
式中:D=Newmark位移(cm);PGA、PGV、Ia和ac的单位分别是g、cm/s、m/s和g。
4.2 基于机器学习的Newmark位移预测模型
WANG等[15]基于深度学习和Newmark位移提出的预测模型(简称“XGB模型”),该模型在位移预测方面具有良好的泛化能力,并通过优化超参数防止数据过拟合。所开发的数据驱动的Newmark位移预测模型能够更好地满足充分性和效率标准,与传统经验模型相比,其产生的标准偏差也小得多,并对模型在概率地震边坡位移危险性分析中的应用进行了论证。XGB模型的残差表达式如下:
(16)
5 危险性结果对比分析
在第3节通过蒙特卡罗方法得到的地震目录,其中包括震级、断层距、断层类型和边坡条件场地等地震信息。基于模拟的地震目录中的参数,利用CAMPBELL等[23]提出的GMPEs(CB14)计算出PGA、PGV和Ia三个IMs的均值及方差。再根据IMs的方差和IMs之间的相关系数,通过蒙特卡罗模拟生成具有相关性特征的IMs的残差,加上利用GMPE计算出的IMs的均值,得出具有空间相关性的IMs模拟值,将其作为三种模型(SR08、SR08_up和XGB)的输入。通过对比相同年平均超越率下的滑坡永久位移,分析是否考虑IMs的相关性造成的差异。
IMs的相关性是指IMs之间的关联程度,用相关性系数表示IMs相关性强弱。一般采用Pearson线性相关系数表示IMs的相关性。BRADLEY[24-25]利用NGA-West1数据库中的1 842条地震动数据,使用GMPEs和Pearson线性相关系数来确定相关性,建立了PGA、PGV和Ia等IMs的经验线性相关系数计算方程。本文中使用了该参考文献中相关性系数中值:IMs的自相关系数为1,PGA和PGV的相关系数为0.733,PGA和Ia的相关系数为0.83,Ia和PGV的相关系数为0.74。
5.1 不同临界屈服加速度ac
将IMs(PGA、PGV和Ia)和ac值分别带入SR08、SR08_up和XGB模型中,计算滑坡永久位移,根据式(1)即可得到三种断层距和三种场地类别下的地震滑坡危险性。如图4所示为SR08_up模型,C类场地下不同ac下地震滑坡危险性曲线。
图4(a)、图4(b)和图4(c)分别对应近中远三种距离场地。图4(a)中:ac=0.02 g时实线和虚线相互重合,ac=0.1 g时,在重现期为4 975 a(50 a超越率为1%)时,考虑IMs相关性的位移是81.26 cm,不考虑时位移是47.40 cm;ac=0.3 g时,在重现期为4 975 a时,考虑IMs相关性的位移是9.14 cm,不考虑时位移是3.35 cm。可见:随着ac的增大,IMs相关性对滑坡危险性影响增加。图4显示:随着ac值的增加,危险性曲线呈现逐渐往x轴偏移的现象。图4(c)中:ac=0.3 g时没有曲线,是因为模型预测对于远场且处于良好地质条件的边坡(临界加速度值为0.3 g),滑坡位移预测值几乎都小于1 cm,使得曲线不在所示坐标范围内。
对比图4(a)和图4(b)ac=0.02 g时,是否考虑IMs相关性对其滑坡危险性影响不大;当在近场时,ac=0.3 g时,在重现期为100 000 a(1 000 a 超越率为1%)时,考虑IMs相关性的位移是104.50 cm,不考虑时位移是27.30 cm;当在中场时,ac=0.3 g时,在重现期为100 000 a时,考虑IMs相关性的位移是7.68 cm,不考虑时位移是小于1.00 cm。所以,在ac=0.3 g时,随着断层距的增加,考虑IMs相关性的影响在增大。在进行危险性评估时不考虑IMs相关性会低估其危险性,极有可能造成滑坡风险隐患。
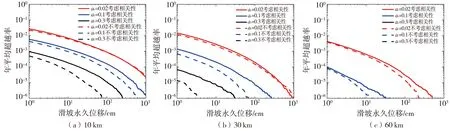
图4 断层距为(a)10 km、(b)30 km和(c)60 km时不同ac地震滑坡危险性曲线Fig. 4 Seismic landslide hazard curves of different ac when the fault distance is (a)10 km,(b)30 km and (c)60 km (solid line means considering correlation,dashed line means not considering correlation)
5.2 不同永久位移模型
为了研究在不同永久位移预模型下考虑IMs相关性的差异影响,选择SR08、SR08_up和XGB三种模型。图5表示在ac=0.1 g和C类场地情况下,基于三种预测模型是否考虑IMs相关性计算出的地震滑坡危险性曲线。根据图5(a)在近场时,SR08、SR08_up和XGB模型在高风险水平时考虑IMs相关性结果差异较大,SR08和SR08_up模型预测位移值偏高;而根据图5 (b),SR08、SR08_up和XGB模型在高风险水平时考虑IMs相关性差异变小。若重现期为100 000 a,当在近场时,XGB模型考虑IMs相关性的位移是298.50 cm,不考虑时位移是213.95 cm;当在中场时,考虑IMs相关性的位移是78.00 cm,不考虑时位移是34.00 cm,相差大于2倍。所以当断层距增大,如果不考虑IMs相关性进行危险性评估时低估其危险性,极有可能造成滑坡风险隐患。同时,图5(b)和图5(c)也可以发现:当断层距增大,实线和虚线对于不同模型基本重合,是否考虑IMs相关性对不同模型之间差异较小。

图5 断层距为(a)10 km、(b)30 km和(c)60 km时不同模型地震滑坡危险性曲线Fig. 5 Seismic landslide hazard curves of different models when the fault distance is (a)10 km,(b)30 km and (c)60 km (solid line means considering correlation,dashed line means not considering correlation)
5.3 不同场地类别
为研究是否考虑IMs相关性在不同场地类别条件下的影响规律,我们选取B、C和D三类场地类别。图6(a)、图6(b)和图6(c)分别表示在ac=0.1 g和三类场地情况下,分别为近、中和远场时是否考虑IMs相关性对不同场地类别的影响。对比图6(a)、图6(b)和图6(c)可以发现:若重现期为100 000 a,近场B类场地考虑IMs相关性的位移是198.20 cm,不考虑时位移是124.30 cm;当远场时,B类场地考虑IMs相关性的位移是是8.35 cm,不考虑时位移是2.00 cm,相差约4倍。所以当断层距增大,IMs相关性对场地的影响增大。在同样风险水平情况下,D类场地的预测位移值最大是因为土体具有放大效应。如果不考虑IMs相关性进行危险性评估时低估其危险性极,有可能造成滑坡风险隐患。
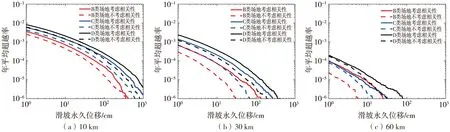
图6 断层距为(a)10 km、(b)30 km和(c)60 km时不同场地类别地震滑坡危险性曲线Fig. 6 Seismic landslide hazard curves of different site types when the fault distance is (a)10 km,(b)30 km and (c)60 km (solid line means considering correlation,dashed line means not considering correlation)
5.4 不同断层距
为研究是否考虑IMs相关性在不同断层距条件下地震滑坡危险性的影响规律,选取10、30和60 km三种断层距,代表近、中和远三种场地距离。取在ac=0.1和SR08_up模型下不同断层距地震滑坡概率危险性曲线,如图7所示。图7(a)、图7(b)和图7(c)分别是对应B、C和D三类场地类别。在C类场地下,若重现期为100 000 a,近场时,考虑IMs相关性的位移是490.55 cm,不考虑时位移是282.13 cm ;当为远场时,考虑IMs相关性的位移是6.65 cm,不考虑时位移是4.67 cm。可见:断层距越大,IMs相关性的影响越小。对同一种场地类别,随着断层距的增加,滑坡永久位移在降低。对比图7(a)、图7(b)和图7(c)可以发现C类和D类场地下考虑IMs相关性对不同断层距的影响相似。在不同场地类别条件下,如果在进行危险性评估时不考虑IMs相关性对断层距的影响会低估其预测位移值和地震滑坡危险性。
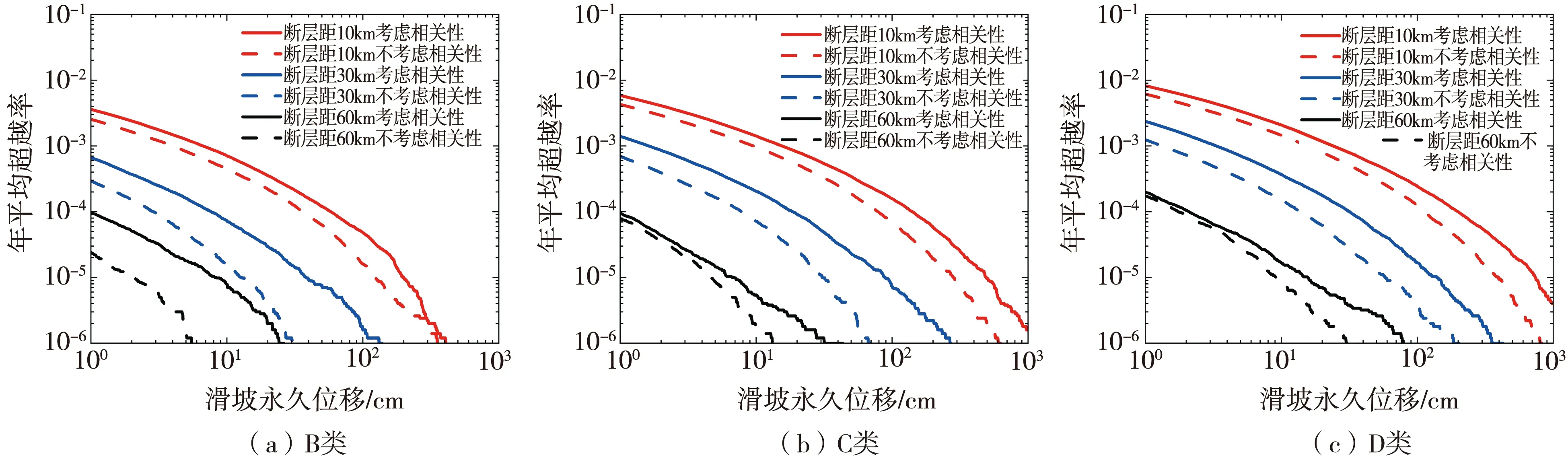
图7 场地类别为(a)B类、(b)C类和(c)D类时不同断层距地震滑坡危险性曲线Fig. 7 The seismic landslide hazard curves of different fault distances when the site type is (a) type B,(b) type C and (c) type D
6 结论
本文基于地震滑坡危险性的全概率分析方法,结合蒙特卡罗模拟,研究在不同临界屈服加速度ac、永久位移预测模型、场地类别和断层距情况下,是否考虑IMs相关性对地震滑坡危险性评估的影响规律,为更加准确预测滑坡位移来降低滑坡风险以及为滑坡防护措施提供理论依据和参考。总的来说,对不同ac、永久位移模型、场地类别和断层距,在进行滑坡危险性分析时,不考虑IMs相关性会造成预测位移值偏小,地震滑坡危险性预估偏低。具体主要结论如下:
1) 不同临界屈服加速度ac:当ac较小,如ac=0.02 g,且为近中场时,可以忽略IMs相关性对地震滑坡危险性的影响;当ac较大时,如ac=0.3 g,随着断层距的增加,相关性对危险性的影响在增大;当ac与断层距同时增大时,IMs相关性对滑坡危险性的影响也在增加。
2) 不同永久位移预测模型:若考虑IMs的相关性,SR08和SR08_up位移预测模型在近场的高风险水平的永久位移值将会偏高;在中场时,高风险水平的永久位移值与观测位移值的绝对误差将会减小;随着断层距的增加,对于不同模型考虑相关性造成的绝对误差数值基本一致。
3) 不同场地类别与断层距:在近中场时,B类场地的危险性水平比C和D类场的地低,但随着断层距的增加,IMs相关性对不同场地类别带来的影响增大。在各类场地上,断层距越大,IMs相关性的影响越大。在各类场地相同风险水平下,由于D类场地具有放大效应,该类场地上的边坡滑坡位移值最大。
