粘弹性人工边界单元及地震动输入方法比较研究
2023-05-12景立平陆新宇齐文浩
王 展,景立平,3,陆新宇,齐文浩
(1.中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080;2.地震灾害防治应急管理部重点实验室,黑龙江 哈尔滨 150080;3.防灾科技学院,河北 三河 065201)
0 引言
近场波动一般是复杂介质中三维非线性问题,通常采用数值计算方法求解。发展近场波动数值模拟技术的目标是在保证数值精度和数值稳定性的条件下不断提高计算效率。作为近场波动问题的重要组成部分,人工边界理论及技术是实现这一目标的必经之路。人工边界需要模拟无限域对计算区域的作用,使两者对计算区域的作用一致,保证散射波透过人工边界或者被人工边界吸收而不会反射回计算区域。常用的人工边界主要有:粘性边界、透射边界[4]、无限元边界[5]、粘弹性边界和自由度绑定边界[7,24]等。DEEKS等[6]1994年推导了柱坐标系下剪切波和膨胀波波动方程,建立了平面应变边界条件。随后,刘晶波等[3]给出了粘弹性边界的一种外源荷载输入方法[13],建立了三维粘弹性人工边界。赵密[22]通过远场平面波的格林函数解,考虑无衰波和衰减波混合并加以推广,得出了粘弹性边界的广义表达形式。刘晶波等[1,23]提出了一致粘弹性边界的概念,并在此基础上提出了一致粘弹性边界单元,这种边界单元和粘弹性边界有相同的模拟精度。刘晶波等[2]2018年提出了一种基于子结构的外源地震动输入方法,弥补了粘弹性边界单元无法有效输入外源荷载的问题。
数值模拟技术发展的同时,还应考虑到使用者的应用方便。粘弹性因为其明显的优点被很多人接受,但是粘弹性边界在实际操作中需要在每个边界节点上施加两个(三维为三个)相互垂直并联的弹簧阻尼元件,并且弹簧阻尼元件的参数与土层材料的参数和节点对应的面积有关,这意味着对于非均网格计算模型,需要逐个单元进行复杂的大量计算,不利于推广使用。同时,地震动输入方法是能否得到合理数值解答的关键。现在主流的地震动输入方式是波动法[8],虽然模拟精度较高,但是需要在每一时步计算每个边界节点的集中力,并判断集中力的作用方向,操作复杂且繁琐。
本文引用了一致粘弹性边界的概念,对与粘弹性边界有相同计算精度的粘弹性边界单元进行了推导,这种边界只需要将单元向外延伸一定宽度,并且赋予其和相邻内部单元材料相关的属性即可。同时采用刘晶波提出的一种基于局部人工边界的子结构的地震动输入方法,避免繁琐的边界节点力的计算和方向判断,且适用于各种应力型局部人工边界。对于外延宽度的取值,李述涛等[11]对于粘弹性边界单元计算稳定性做了讨论,给出了侧边子系统和角点子系统的稳定条件,可通过此稳定条件确定小变形下的边界单元宽度。基于此,本文考虑大变形时粘弹性边界单元的适用性,以底边界输入位移幅值umax和边界单元宽度b的比值ε=umax/b为参数考虑此影响。数值算例表明:当ε≤0.1时,计算结果误差较小,并以脉冲输入的散射场作为算例进行了验证。
1 一致粘弹性人工边界
1.1 粘弹性边界理论
粘弹性边界是在人工边界上施加并联弹簧元件和阻尼元件,用来模拟无限域对有限计算区域的作用。其中弹簧元件和阻尼元件的参数是根据空间柱面波或球面波理论解确定。
粘弹性人工边界的弹簧系数KB和阻尼系数CB分别为:
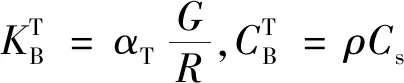
(1)
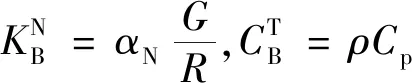
(2)
式中:G表示介质的剪切模量,R表示加载点到人工边界的距离,ρ表示介质的质量密度,Cs和Cp分别表示介质的剪切波速和压缩波速,αT和αN分别表示切向和法向弹簧的修正系数,其取值参考刘晶波推荐值,见表1。
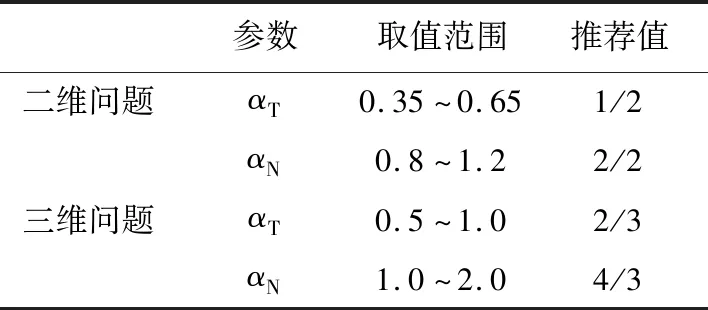
表1 弹簧修正系数取值Table 1 Spring correction factor
1.2 二维一致粘弹性边界
用有限单元法对模型进行空间离散化时,粘弹性人工边界也随之离散,如果将组成粘弹性边界的弹簧阻尼元件看作一个单元,其形函数若与内部单元相同,认为这样离散后的边界为一致粘弹性边界。
为了推导一致粘弹性边界的刚度矩阵和阻尼矩阵,将内部单元与粘弹性边界相邻的一条边视作杆件单元,i和j表示单元的两个节点,2L表示杆长。此时,认为最外侧杆单元的形函数和由弹簧阻尼元件组成边界的形函数相同。
(3)
假设法向和切向有相同的形函数,杆件单元的形函数矩阵为:
(4)
边界上分布的弹簧的弹性刚度矩阵为:
(5)
根据虚功方程δW外=δW变,注意到不同于一般的单元,连续分布弹簧的所接受的总虚变形功等于所有弹簧变形功之和,连续分布弹簧接受总虚功为:
(6)
外力所做的总虚功为:
(7)
由δW外=δW变,将式(6),(7)带入可得:
(8)
式(6)、式(7)和式(8)中:δδB为虚位移,S和p(x)分别表示内部单元作用在边界单元节点上的力和作用在边界单元内部的分布力。
由单元刚度方程得:
(9)
然后将式(4)和式(5)带入式(9)中,得到二维一致粘弹性人工边界单元的单元刚度矩阵:
(10)
将上面推导过程中的弹簧力用阻尼力替代,使用和上面推导完全相同的方法即可以得到二维一致粘弹性人工边界单元的阻尼矩阵:
(11)
2 等效二维一致粘弹性边界单元
2.1 等效二维一致粘弹性边界单元刚度矩阵
考虑到实际应用的方便,寻求一种常用的实体单元等效代替连续分布的弹簧阻尼元件,为实体单元赋予相应的阻尼和弹性模量,实现和连续分布的弹簧阻尼元件相同的作用,因为这种边界单元与内部单元有相同的形函数,所以认为是一致粘弹性边界单元。采用二维有限元最常用的四节点矩形单元,来实现这一想法。如图2所示为四节点矩形人工边界单元。
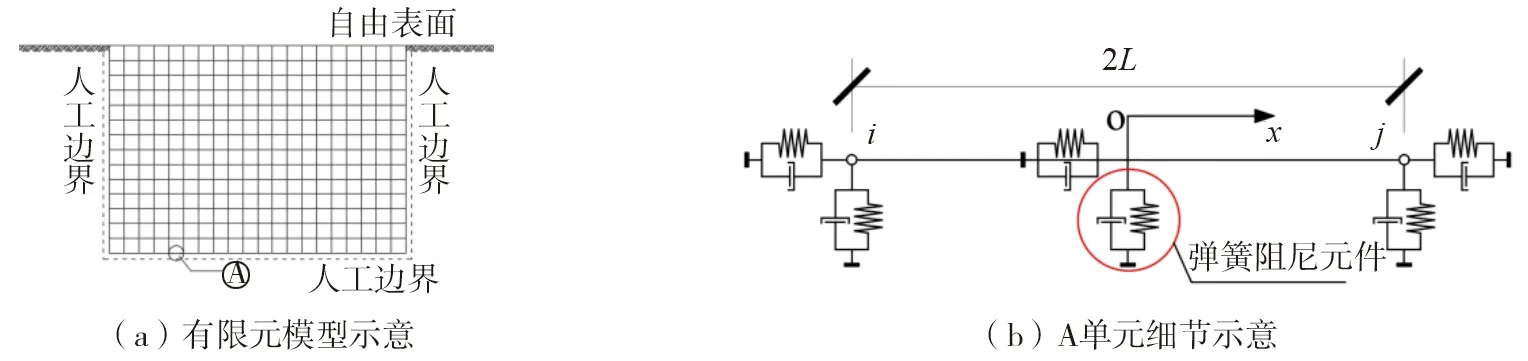
图1 二维一致粘弹性边界单元示意图Fig. 1 Schematic diagram of two-dimensional uniform viscoelastic boundary element

图2 矩形边界单元Fig. 2 Rectangular boundary element
令:
(12)
根据有限单元法基本原理[10],推导平面应变时等效刚度矩阵如下:
(13)
为了将四节点矩形单元和一致粘弹性边界单元联系起来,当b趋于0时,可以将式(13)写成如下形式:
(14)
上飘“~”表示等效参数。其中:E表示弹性模量,μ表示泊松比。对比式(14)和式(10),两矩阵完全相等,应该有下式成立:
(15)
由式(15)、式(1)和式(2)可推得边界单元的等效弹性模量和等效剪切模量为:
(16)

2.2 等效二维一致粘弹性边界单元阻尼矩阵
假设等效二维一致粘弹性边界单元阻尼矩阵和刚度矩阵成正比,即:
[Ce]B=β[Ke]B
(17)
其中:
(18)
将式(1)、式(2)、式(10)、式(11)和式(18)代入式(17),可得:
(19)
2.3 边界验证算例
由于边界单元无法分开施加切向阻尼和法向阻尼,本算例中切向和法向阻尼系数采用表2中几种不同的组合,进行计算比较,并和远置边界、粘弹性边界和粘性边界计算结果进行对比。计算工况见表2。

表2 工况表Table 2 Table of working condition
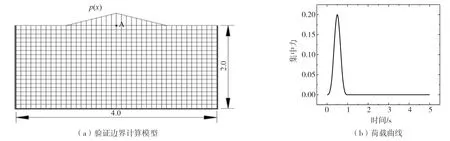
图3 验证边界模型及荷载曲线Fig. 3 Calculation model of verifying boundary and Loading curve

图4 不同边界计算结果对比Fig. 4 Comparison of calculation results of different boundaries
(20)
3 基于子结构的地震动输入方法
局部人工边界主要特征是时空解耦,即一个边界节点在某一时刻的运动仅与其相邻节点在相邻时刻的运动有关,而与其他节点和其他时刻无关。基于这个特征,刘晶波等[2]提出了一种适用于各类应力型局部人工边界的地震动输入方法,通过在包含人工边界的子结构模型中输入节点位移或加速度,经过局部子结构动力分析即可获得相应节点的等效荷载。这种方法可以避免繁琐复杂的边界节点应力的计算。具体实现步骤见图5。

图5 子结构法施加地震荷载流程图Fig. 5 Flow chart of applying seismic load by substructure method
4 不同人工边界和地震动输入方法组合的对比
4.1 自由场脉冲荷载输入
为了验证人工边界单元和地震动输入方法的模拟效果,数值试验如下。计算输入为底部垂直入射的SV位移脉冲,如图6(b)所示,脉冲持时0.2 s,幅值为0.1 m,计算时长1 s。有限元模型如图6(a)所示,模型尺寸为40 m×30 m,网格尺寸为1 m×1 m,介质密度为2 500 kg/m3,泊松比为0.25,剪切波速为200 m/s,杨氏模量为2.5×108Pa。计算工况见表3。

表3 不同的边界条件地震动输入方法Table 3 Ground motion input methods of different boundary condition

图6 自由场计算模型及输入位移曲线Fig. 6 Calculation model of free field and Displacement curve

计算结果如图7所示。工况3.1与工况3.2计算所得结果和理论值的拟合度最高。工况3.3同样能够得到较为精确的结果,但是总体精度比工况3.1与3.2得到的结果精度低,这是因为粘弹性边界单元在推导时假设了单元宽度较小并且阻尼系数使用切向和法向阻尼系数的平均值。虽然经学者研究[9],粘弹性边界单元具有较好的鲁棒性,但是并不能完全吸收外行波,少量的反射波仍会引起一点误差。工况3.4采用粘性边界加子结构法,在于说明其他的人工边界同样适用子结构方法输入荷载,由于将输入时程基线调零,并且位移脉冲频率适中,可以很大程度地减小粘性边界的漂移现象;工况3.5作为近似人工边界,在模拟自由场时能够获得较高的精度。

图7 自由场不同点水平位移时程图Fig. 7 Time history of horizontal displacement at different points in free field
4.2 输入幅值与边界单元尺寸比值的影响
由于粘弹性边界单元实质上和普通的有限单元别无二致,当应变较大时,材料的非线性往往不能忽略,并且在进行动力分析时,考虑计算区域内单元材料的非线性经常是必要的,在同一分析步中计算的边界单元也必须考虑过大的应变引起的非线性可能导致的计算误差。考虑大应变可能引起的非线性,再进行有限元模型如图6(a)所示的算例,仅改变输入位移脉冲的幅值,模型材料参数与4.1节相同。以输入位移幅值umax和粘弹性边界单元宽度b的比值ε=umax/b为控制边界变形的参数,分别计算了ε为0.01、0.02、0.05、0.1、0.2和0.5时BE两点的水平方向的位移反应,计算结果如图8所示。结果表明:当ε>0.1时,BE两点的计算结果出现了较大的偏差,并且与理论结果相差较大,当ε≤0.1时,BE两点位移符合理论解答。表4给出了计算结果与理论结果的差值。误差使用式(21)表示。
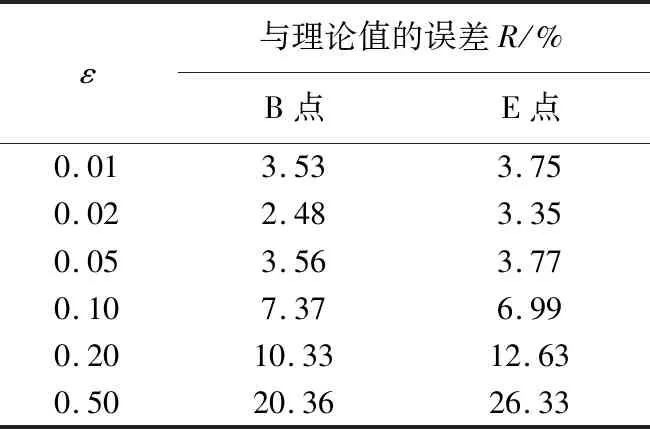
表4 BE两点计算结果与理论值的误差Table 4 The errors of the points BE between numerical results and theoretical values
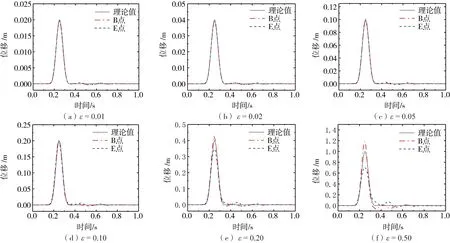
图8 粘弹性边界单元不同ε时模型BE两点水平位移Fig. 8 Horizontal displacement of the model at points B and E with different ε
(21)
综上所述,说明粘弹性边界单元的应变对其模拟结果有一定影响,当其应变较大时,计算结果出现明显偏差。建议人为控制ε≤0.1,可以获得可信度更高的数值模拟结果。
4.3 散射场脉冲荷载输入
建立如图9所示的散射场模型,验证几种人工边界及地震动输入方式的组合用于散射场时的计算精度。模型材料的参数和输入的位移脉冲和3.2节完全相同,模型尺寸如图9所示,计算工况见表3,计算结果如图10所示。从工况3.1、工况3.2和工况3.3计算结果分析,可以得到和3.2节基本相同的结论,说明粘弹性边界和粘弹性边界单元都有较好的适用性,应用于自由场和散射场时都能得到精确结果。工况3.1与工况3.2和远置边界解的拟合度最高,与3.2节自由场算例的不同之处在于:(a)工况3.4出现了明显的漂移现象,这是因为工况3.4采用的粘性边界,只考虑了对外行波的吸收,可能出现模型整体最终受力平衡时,最终速度不为0的情况,这将导致模型整体沿着最终速度的方向一直运动。(b) 工况3.5出现明显震荡,原因在于自由度绑定边界只有在侧边界掠入射的情况下才能有较高的模拟精度,由于不能保证全部散射波到达侧边界时均与侧边界法线成90°夹角,所以计算结果出现较大偏差。
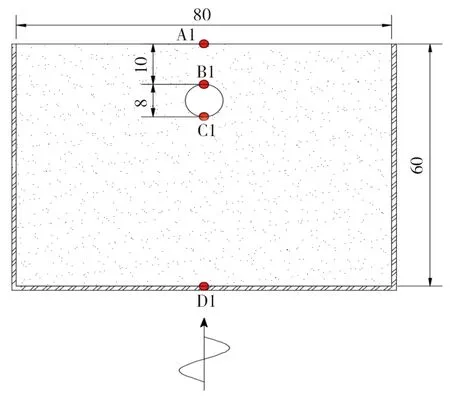
图9 散射场计算模型Fig. 9 Computational model of scattering field
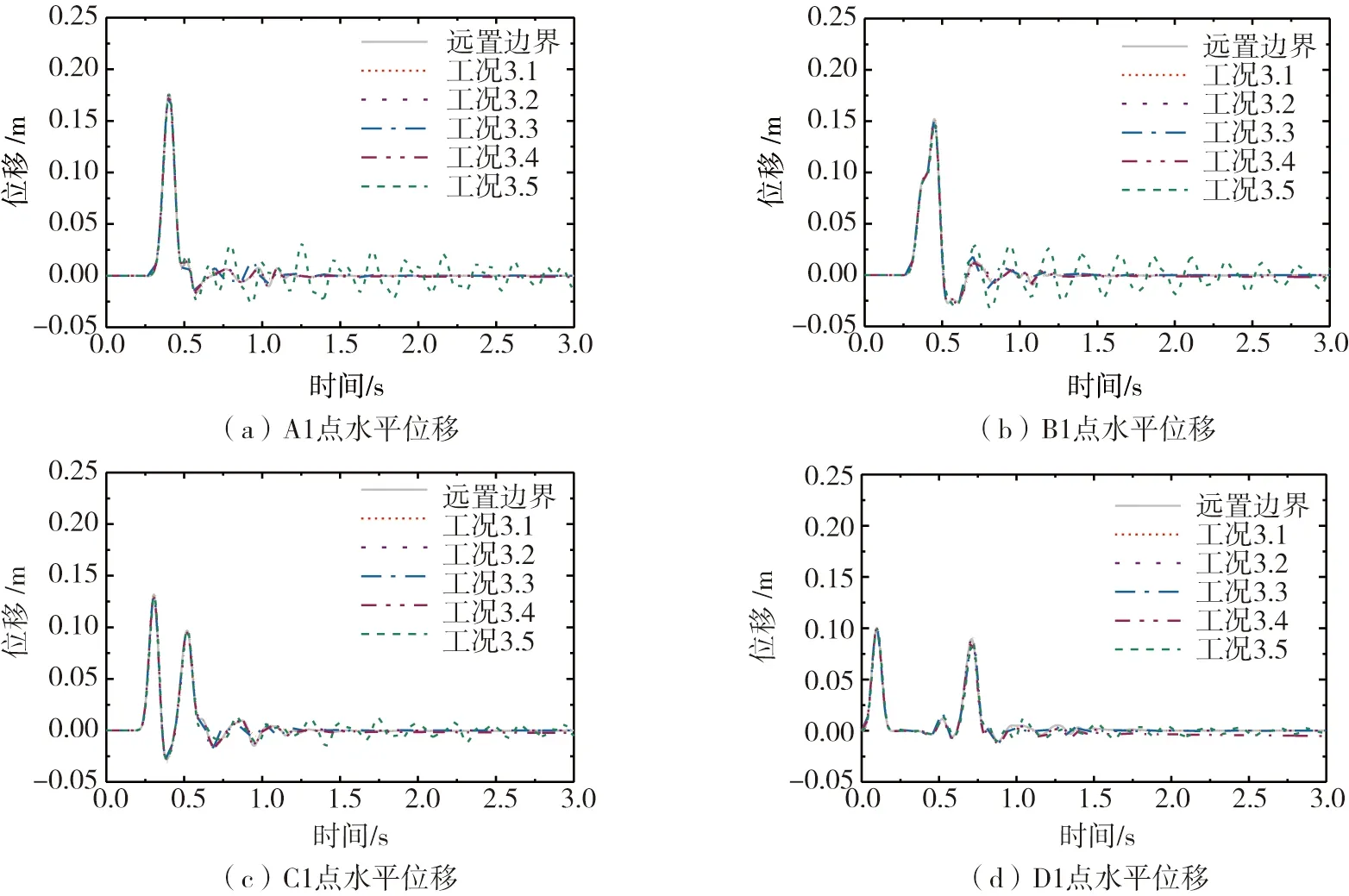
图10 散射场不同节点水平位移时程Fig. 10 Time history of horizontal displacement at different points in scattering field
5 结论
1)粘弹性边界概念清晰,地震动输入子结构法节点力计算准确,两者组合计算精度最高,但是在节点施加弹簧阻尼元件时操作复杂,前处理工作量大。
2)粘弹性边界单元和子结构输入组合模拟精度与集中粘弹性边界和子结构输入组合接近,虽然推导粘弹性边界单元时进行了一些假设,但对实际计算精度并没有很大影响,且有前处理更加简单方便的优点。
3)使用粘弹性边界单元时,边界单元的应变对计算结果有一定影响,建议人为控制ε≤0.1,否则计算结果会产生较大偏差。
4)粘性边界在输入地震动频率合适且输入时程基线校正时,在自由场计算中能得到比较可靠的结果,并且在ABAQUS中容易实现。但是应用于散射场中时,由于散射波的作用,会出现难以预估的漂移现象。
5)侧边界使用自由度绑定边界时可以精确模拟自由场垂直入射情形,但是对于散射场计算(工况3.5)精度较低,建议在计算散射场时谨慎使用。
