光纤线包固化残余应变应力与变形数值模拟
2023-05-12王宇东马保吉孟晓彤
杨 帆,王宇东,马保吉,孟晓彤
(1 西安现代控制技术研究所,陕西 西安 710065;2 西安工业大学兵器科学与技术学院,陕西 西安 710012)
0 引言
光纤传输图像制导技术具有命中精度高、抗干扰性能强、能够实现人在回路的闭环制导等优点,是精确制导武器的重点发展方向。光纤线包是指按照一定的排列规则将制导光纤精确缠绕在线轴上形成的纺锤形实体,用于实现制导武器与作战平台之间数据双向传输。为了保证光纤在缠绕、存储、运输中的稳定以及在使用时高速有序释放,在光纤线匝和层间涂覆粘结剂并进行固化工艺处理,粘结剂的固化提高了线包稳定性。但由于线包材料的力学特性和热特性差异,厚度方向几何尺寸较大,固化时线包表面与内部产生了由不均匀热膨胀造成的热应力[1],同时固化过程中粘结剂由液态变为固态也产生体积收缩变形及由此产生的应力。不均匀热应力和固化收缩应力使线包出现裂缝、光纤挤出和跨线点滑移等缺陷[2-3],导致光纤释放出现断纤、脱匝、缠结等放线失败风险增加。预测和控制固化工艺产生的残余应力和变形具有重要意义。由于光纤尺寸、材料和结构特殊性,测量线包内部应力和变形分布以及由此产生的几何缺陷很困难。徐振华[4]曾通过X射线扫描方法检测线包内部缺陷,但由于线包材料对X射线吸收率存在较大差异,分辨率很难保证。杨在友[5]用工业CT机对线包层状结构进行检测,结果显示CT机对于线包层状结构的区分度不敏感。
光纤线包内部结构与固化过程在一定程度上与纤维增强树脂基复合材料热压成型层合板固化过程有相似之处,数值模拟技术在层合板成型残余应力和变形预测的成功经验[6],为线包固化残余应力和变形预测提供了一种手段。由于缠绕层数较大,既有光纤之间的线接触,也有粘结剂与光纤的面接触,还有粘结剂和光纤与线轴之间的接触,准确建立数值模拟的几何模型及离散化难度较大。 同时线包固化过程涉及热传导、粘结剂交联反应、固化收缩、热膨胀、固化变形等相互耦合的物化作用,并且其材料具有粘弹性效应和时变特性,使得其数学模型建立和耦合求解需要进一步研究[7]。
针对上述问题,文中在分析线包材料时变特性和粘弹性效应基础上,建立了包括热膨胀和化学反应效应的线包残余应力广义MAXWELL本构模型。采用热-化学反应-结构间接耦合方式,利用ANSYS APDL技术对线包固化工艺中残余应力和变形进行了数值模拟,并对固化温度、降温速率以及线包缠绕层数对固化变形的影响进行了分析,为光纤线包固化工艺的确定和优化提供了一种有效方法。
1 线包固化残余应力应变模型
线包在固化过程中会发生3种方式的应变:1)线包中光纤和粘结剂硅橡胶由于温度分布不均匀引起的热应变;2)粘结剂硅橡胶化学体积收缩应变;3)由于线包与线轴材料不匹配而在固化过程中引起的线包与线轴的接触应变。
为对线包固化完成之后的残余应力进行模拟,要建立线包固化残余应力应变模型。
1.1 热应变
增量步内的线包内部热应变可表示为:
εkl,t=αiΔT
(1)
式中:i=1,2,3;αi为线包3个等效材料方向上的热膨胀系数,可通过细观力学混合率公式计算得到[8]:
(2)
式中:α1为线包沿光纤缠绕方向上热膨胀系数;α1f为平行于光纤缠绕方向光纤热膨胀系数;E1f为平行于光纤缠绕方向光纤模量;Vf为线包中光纤所占体积分数;αm为粘结剂硅橡胶热膨胀系数;Em为粘结剂硅橡胶模量。
对于线包轴向热膨胀系数,如果将光纤等效为各向同性材料,则可以表示为:
α2=αfVf+(1+vm)αmVm
(3)
式中:α2为线包轴向热膨胀系数;αf为各向同性光纤的热膨胀系数;vm为粘结剂硅橡胶的泊松比。
如果将光纤等效为横观各向异性材料,线包横向热膨胀系数可表示为:
(4)
式中:α1f和α2f分别为横观各向同性光纤平行于光纤方向和垂直于光纤方向的热膨胀系数。
1.2 收缩应变
假设一个粘结剂硅橡胶单元,其长、宽、高的体积尺寸分别为l1,l2,l3,固化反应完成后,3个方向上的体积尺寸变化量分别为Δl1,Δl2,Δl3,则这个硅橡胶单元的体积变化量ΔV为:
ΔV=Δl1l2l3+l1Δl2l3+l1l2Δl3+Δl1Δl2l3+
l1Δl2Δl3+Δl1l2Δl3+Δl1Δl2Δl3
(5)
体积变化量与原体积比值即为粘结剂体积收缩率Δv,其表达式为:
Δv=ε1+ε2+ε3+ε1ε2+ε1ε3+ε2ε3+ε1ε2ε3
(6)
因为粘结剂硅橡胶作为一种各向同性材料,3个主要材料方向上收缩和应变量都相等,则粘结剂硅橡胶各向同性收缩,其应变量可表示为[9]:
(7)
固化过程中,硅橡胶的体积变化率与固化程度和固化完成后总体积变化率Vsh有关,即:
Δv=Δα·Vsh
(8)
因此粘结剂硅橡胶的收缩应变εm,c为:
(9)
同计算线包热膨胀系数的原理相似,线包的化学收缩应变为:
(10)
ε2,c=ε3,c=(εm,c+vmεm,c)(1-Vf)-(vm(1-Vf))ε1
(11)
线包热化学应变方程通过对热应变与化学应变之间的求和公式计算得到:
εkl,tc=εkl,t+εkl,c
(12)
式中:εkl,t为热应变;εkl,c为化学应变。
1.3 固化残余应力模型
由于粘结剂硅橡胶的热物理材料特性和力学材料特性会随着其固化程度和温度的变化历程而发生变化,所以固化残余应力应变是固化程度和温度的函数。考虑复合材料成型过程中的黏弹性效应,采用广义MAXWELL黏弹性本构模型,本构方程式为[9]:
(13)
式中:σij为线包的应力分量;εkl为线包的总应变;εkl,tc为线包的化学收缩应变;Qij为材料刚度系数;i,j=1,2,3。
粘弹性本构方程的增量形式为[10]:
Δσi,t+Δt=QijΔεj,t+Δt+Δσi,r
(14)
利用广义MAXWELL模型结合Prony级数,Qij可表示为[10]:
(15)
式中:Wm为第m个MAXWELL单元的权重因子;τm为第m个MAXWELL单元松弛时间;Qij,∞和Qij,0分别为平衡刚度和初始刚度;ξ为缩减时间。
而Δσi,r可表示为:
(16)
由于光纤缠绕方向都是沿着线轴周向,垂直于光纤缠绕方向的截面上光纤和粘结剂规则分布,光纤线包的结构和横观各向同性复合材料结构相同,因此可以按照横观各项同性细观力学理论对线包的弹性常数来计算线包的刚度矩阵及其元素[10]:
(17)
(18)
式中:E,G,v分别为弹性模量、剪切模量以及泊松比;下标m,f表示粘结剂和光纤;下标1,2,3表示方向。
模型中温度和固化度可由固化过程中的热传导方程和固化反应速率方程求解获得。
2 固化过程材料物性参数时变特性
从前述数学模型可以看出:线包残余应力和残余应变取决于复合材料各组分的物理特性,而线包固化过程为一个从液态到固态转变过程,伴随着固化反应进行,物性参数会逐渐发生变化。因此,需要明确光纤和粘结剂物性参数随时间的变化规律。
2.1 粘结剂模量
硅橡胶粘结剂的杨氏模量变化可表示为[11]:
(19)
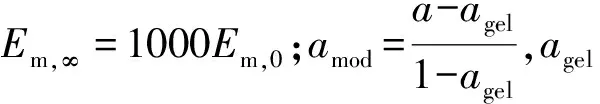
2.2 热传导率
根据细观力学横观各向同性材料混合率公式得到平行于光纤缠绕方向的热导率ky[11]:
ky=Vfkf+(1-Vf)km
(20)
垂直光纤缠绕方向截面两个方向热导率kx和kz为:
(21)
式中:B=2(km/kf-1),kf为光纤热传导系数,kf=0.742+9.02×10-4T;km为粘结剂热传导系数,km=0.0418(3.85+(0.035T-0.41)α)。
2.3 线包等效密度
线包等效密度可表示为:
ρ=Vfρf+(1-Vf)ρm
(22)
式中:Vf,ρf,ρm分别为光纤体积分数、光纤密度、粘结剂的密度。
2.4 热膨胀系数和比热容
粘结剂密度随固化度变化为[9]:
(23)
由复合材料细观力学理论可得线包等效比热容:
(24)
式中:Cm和Cf分别为粘结剂和增强纤维的比热容。
粘结剂比热容Cm可表示为[9]:
Cm=4.184(0.468+5.975×10-4T-1.141α)
(25)
碳纤维比热容可表示为:
Cm=1.390+4.50×10-3T
(26)
粘结剂固化过程中会经历粘流态、橡胶态和玻璃态3个状态,其热膨胀系数可表示为:
(27)
式中:αm,l,αm,r,αm,g分别为粘结剂在粘流态、橡胶态和玻璃态的热膨胀系数。
3 线包固化变形数值模拟方法
3.1 热、化学和结构模型的耦合求解
用ANSYS APDL对间接热-结构耦合方式进行瞬态求解。通过耦合求解热传导方程和固化动力学方程得到线包内部温度和固化度分布以及历程,计算出线包固化过程中粘结剂和光纤的热应变以及收缩应变。考虑温度和固化度的线包材料本构方程计算残余应力与变形。同时线轴在固化工艺温度下产生热应变,线包和线轴产生接触应变,因此残余应变与接触应变构成了线包总应变。应力求解如图1所示。
由于粘结剂固化的材料属性随温度和固化程度变化而变化,需要耦合热传导和固化动力学模型算出实时材料属性,选择适当时间步长对热物理材料属性和力学材料属性进行更新,在每个时间步长内进行热-结构间接耦合。固化过程热-结构间接耦合瞬态求解流程如图2所示。

图1 线包固化残余应力求解关系图Fig.1 Diagram of solving residual stress of cable package curing
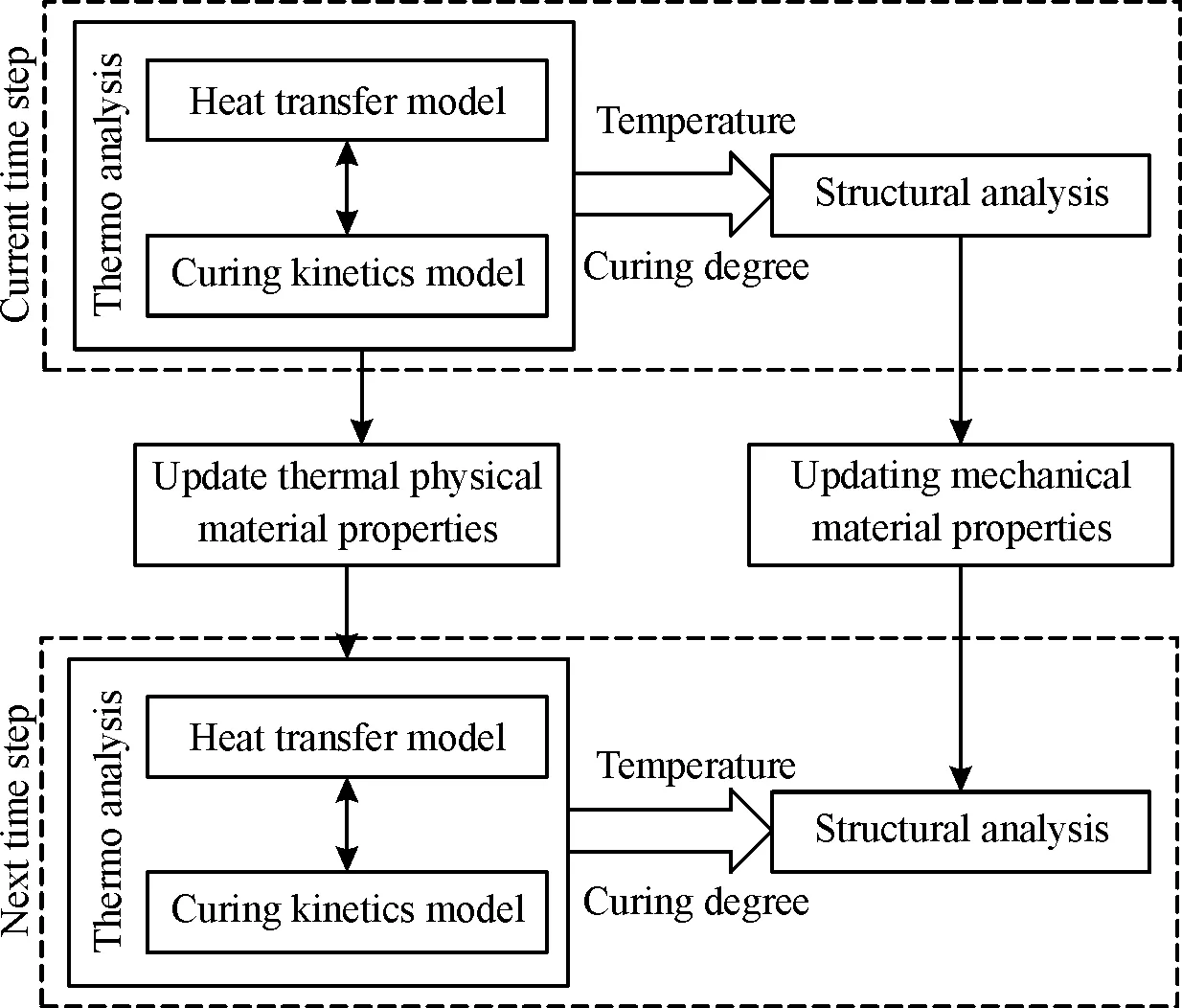
图2 固化过程热-结构间接耦合瞬态求解流程Fig.2 Transient solution flow of heat-structure indirect coupling of curing process
3.2 有限元模型与材料参数
几何模型由实体简化而成,线轴内径103 mm,线轴壁厚5 mm,线轴长度256 mm,初始匝数622,两边退匝数2,缠绕层数70。选三维八节点六面体单元 SOLID70进行热分析,采用扫略网格划分方法进行网格划分。三维有限元模型如图3所示。
线包结构材料特性和粘结剂固化动力学参数以及边界条件与文献[12]相同。

图3 线包三维有限元模型Fig.3 Three-dimensional finite element model of cable package
3.3 有限元模型的求解
固化过程与温度和时间有关,采用瞬态热求解器进行求解。由于线包线轴存在接触以及结构参数的非线性特征,采用非线性求解器求解,过程为:
1)对仿真实体进行有限元建模;
2)施加结构温度边界条件并进行热分析;
3)存贮线包温度分布和固化度分析结果;
4)结构分析前处理,更新线包结构材料参数;
5)读取热分析结果并施加到结构各节点上;
6)对线包结构进行结构力学求解,获得线包应力、应变及变形。
4 数值模拟结果及讨论
4.1 线包固化过程中变形与残余应力分布
图4为线包轴向收缩应变随固化度和时间变化的情况。粘结剂硅橡胶在高温作用下产生固化反应,从而发生化学交联收缩现象,线包内部产生固化收缩应力。在固化初始阶段,虽然粘结剂硅橡胶已有一定程度收缩,但由于此时还处于流体状态,模量极小,几乎无法传递应力,因此初始阶段收缩应变很小。当变为固态后,收缩应变随固化度提高逐渐变大,固化结束后收缩应变将不再发生变化。
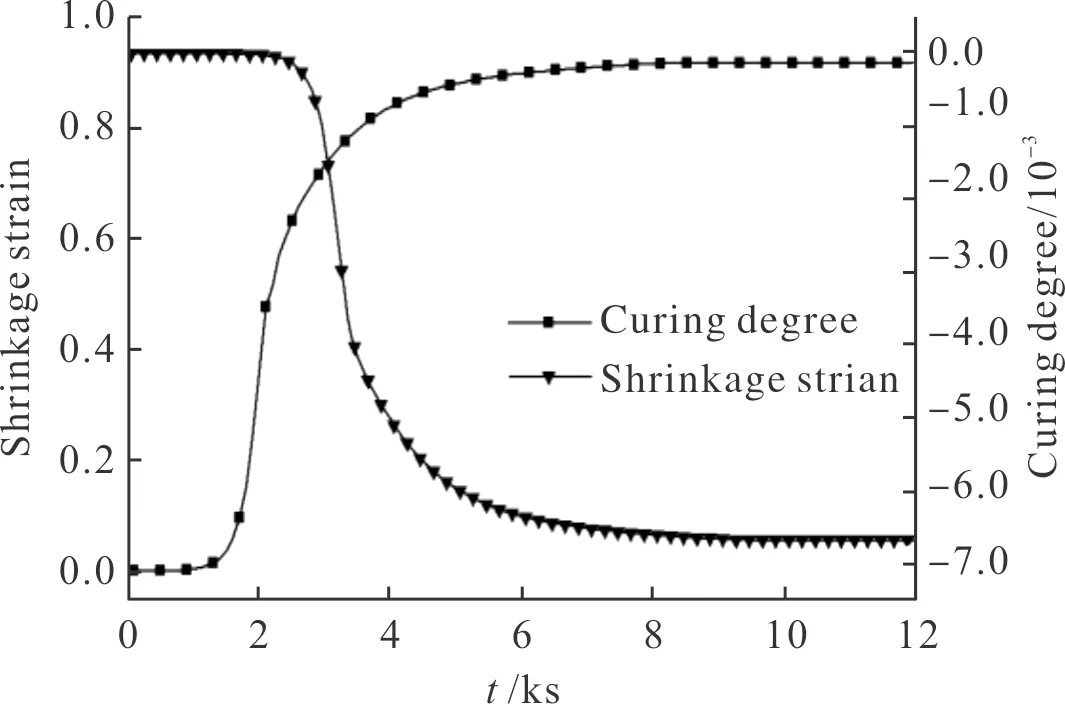
图4 线包轴向收缩应变变化曲线Fig.4 Shrinkage strain curve perpendicular to winding direction
粘结剂硅橡胶虽是匀质材料,理论上任何方向上的收缩量都相同,但平行于光纤缠绕方向上光纤有较高弹性模量,且粘结剂体积分数很小,因此线包平行于光纤缠绕方向收缩应变很小,可忽略。光纤释放时粘结应力主要来自垂直于光纤缠绕方向,因此研究这个方向的固化收缩应变十分必要。
光纤线包收缩应变分布如图5所示,收缩应变最大值0.006 813与最小值0.006 678相差很小,收缩应变均匀分布在整个线包内,收缩应变主要取决于收缩率,因此固化收缩应变均匀分布在线包内。

图5 线包收缩应变分布云图Fig.5 Cloud atlas of shrinkage strain distribution
图6为线包A,B,C三个位置点Von-Mises应力随时间变化曲线,C点位于线包与线轴接触位置,由于铝线轴热膨胀系数比光纤材料大很多,因此在固化高温作用下,线轴会发生更加剧烈热变形,而光纤紧密缠绕在线轴上,并涂有粘结剂,线轴应变会传递到线包上,因此线包与线轴接触初始缠绕层会产生更大应变。固化速率较快时出现拐点,是粘结剂化学收缩较为迅速的时刻,当固化收缩应变短时间大于热应变时出现拐点,温度继续升高后热应变值大于收缩应变值,总应变值便会继续升高。
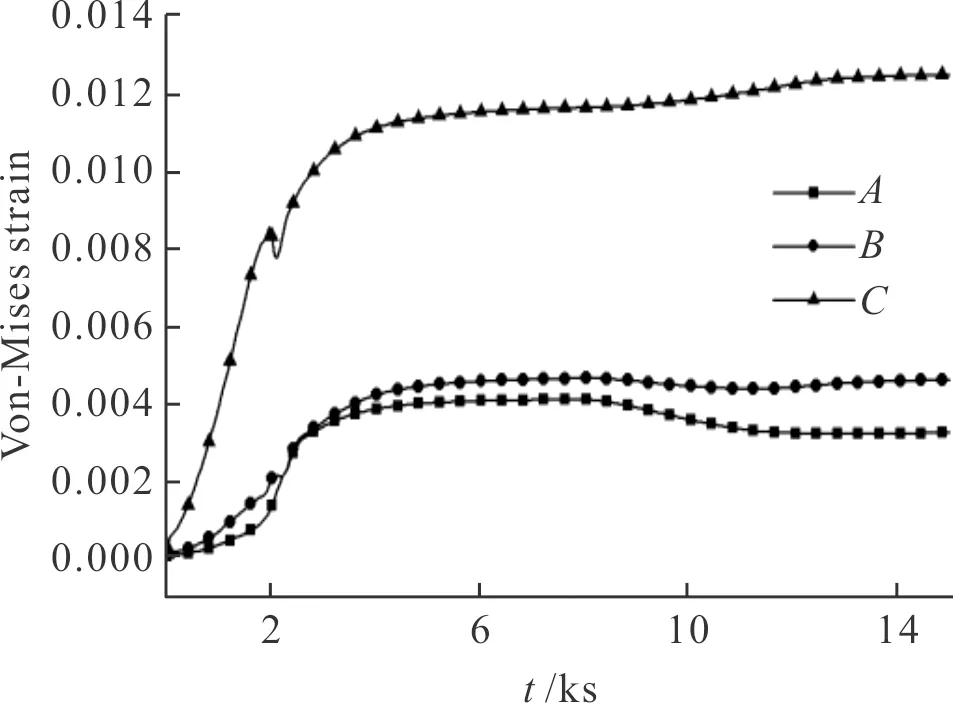
图6 线包关键位置等效应变的随时间变化曲线Fig.6 The curve of equivalent strain at the critical position of cable package with time

图7 结果数据读取点Fig.7 Result data read point
线包整体等效应变分布如图8,等效应变最大值分布在两端跨匝区域,跨匝是让光纤换向缠绕压在下层两匝光纤凹槽里,又不会将下层光纤挤压离开原来位置。跨匝区域抵抗热应力能力小,更易产生应变。光纤在张力作用下紧密缠绕在线轴周向上,线包在周向是闭合环形结构,为了防止在释放时被拉断,光纤具有极高抗拉强度和模量,因此线包沿径向和周向应变会很小。相反,沿线包轴向没有约束和闭合结构,在热应力和收缩应力作用下,应变从线包中间位置沿着线包轴线向两边发展。

图8 线包整体等效应变分布云图Fig.8 Cloud atlas of equivalent strain distribution
固化完成后线包内部正应力分布云图如图9所示,垂直于线包缠绕方向的截面上材料属性各向同性,从图9(a)、图9(b)看出,线包径向和轴向正应力分布情况相似,线包与线轴接触部位应力最集中,主要原因有3个:1)固化时粘结剂迅速释放反应热不能及时扩散,导致线包内部温度差值变大,产生较大热应变;2)线包和线轴材料不匹配,在温度变化时出现不同的热膨胀,线轴与线包相互力作用产生较大应力;3)冷却阶段线包表面和中心位置出现较大的温度梯度,导致应力急剧变大。
线包环向正应力如图9(c)所示,可以看出,线轴及线包与线轴接触部位环向应力为正,且向外渐变为负,这是因为在仿真过程中定义材料沿光纤缠绕方向单元坐标系方向与整体柱坐标Y轴方向相反,即正值为压应力,而负值为拉应力。出现图9(c)中线包与线轴接触部位为环向压应力而向外逐渐为拉应力的原因主要有:沿光纤缠绕方向即环向,线包材料热膨胀系数比线轴材料小,在热应力作用下线轴和线包都会向外膨胀,而线轴膨胀量要大一些;线包材料沿光纤缠绕方向模量要比线轴材料稍大一点,这样就会导致线包与线轴接触部位出现压应力,线包外层出现拉应力。
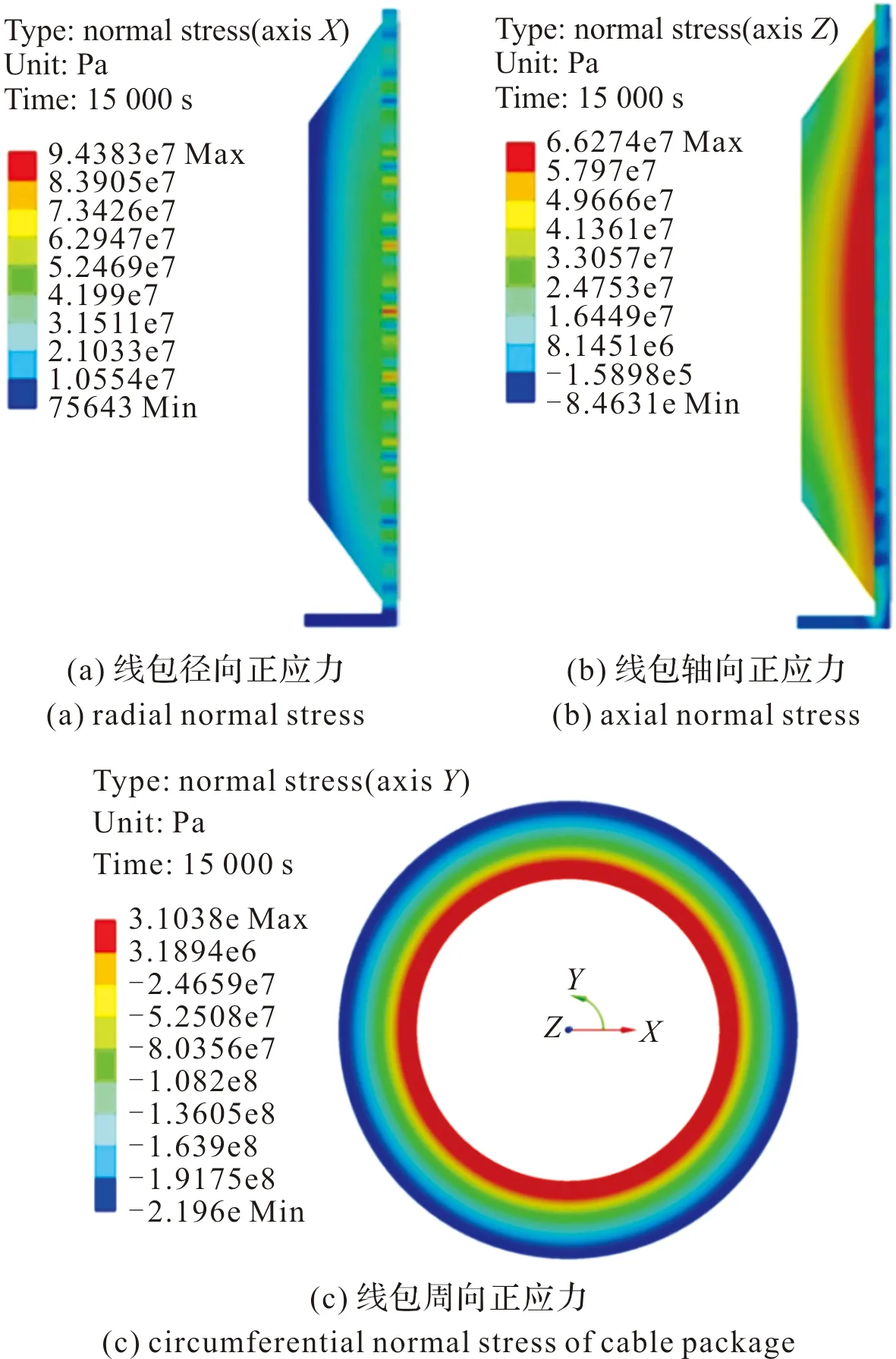
图9 固化完成后线包内部正应力分布云图Fig.9 Cloud atlas of normal stress distribution inside cable package after curing
4.2 固化温度对线包变形的影响
选择固化温度为135 ℃、145 ℃、155 ℃、165 ℃、175 ℃来研究温度对线包变形的影响,升温速率为5 ℃/min,135 min完成固化,之后降温到25 ℃。
图10为最大固化变形量随温度变化曲线,可以看出,变形随着温度升高而增大。

图10 最大固化变形量随固化温度变化曲线Fig.10 Curve of maximum curing deformation with curing temperature
验证了固化温度对固化均匀性的影响,温度提高使线包表面与内部温度梯度变大,空间上热膨胀量出现更大的梯度变化。较大的温度梯度使梯度方向上线包的力学性能和粘结剂固化收缩不一致。曲线斜率随固化温度升高变大,温度对变形的影响程度随固化温度升高更加显著。
4.3 不同缠绕层数的固化变形分析
光纤缠绕层数是指光纤依次从底层开始以纺锤体形状向上缠绕的层数,缠绕层数多少与光纤总长度、导弹外形尺寸、线轴直径、光纤直径有关。但层数优化设计时未考虑线包固化工艺特性。厚度较大的线包固化热量传递到线包中心更加缓慢,这将导致线包更加不均匀的温度和固化度分布。
选层数为50,60,70,80,90的线包,在相同固化工艺下进行固化变形仿真,结果如图11。随着线包缠绕层数变大,等效残余应力变大,但是线包最大变形量却随着厚度增大而变小。以二氧化硅和硅橡胶为主要材料线包的热传导系数比较低,粘结剂固化反应放热量与固化温度传导热量会使得线包在厚度方向产生较大温度梯度,导致较大固化度梯度,缠绕层数越大,径向厚度越大,温度和固化度梯度就会越大。不均匀固化度和温度是导致固化残余应力与固化变形主要原因。线包厚度变大,抗弯截面系数会变大,在相差不是很大弯矩的作用下,线包缠绕层数越大,线包的形变量反而会变小。

图11 层数影响线包固化最大形变和等效应力曲线Fig.12 Maximum deformation and equivalent stress curves of cable package with different winding layers
5 结论
考虑光纤线包材料在固化过程的粘弹性效应和时变特性,建立了描述固化过程中线包变形和残余应力的数学模型,采用间接耦合有限元方法对线包固化过程中变形和残余应力进行了数值模拟,分析了固化温度、降温速率和线包缠绕层数对固化变形和残余应力的影响,主要结论如下:
1)在固化初始阶段,热化学收缩是线包变形的主导因素,随着粘结剂的固化程度增大而增大,且变化较大;完全固化后,线包变形随时间变化很小。
2)由于铝合金线轴的热膨胀比线包复合材料大得多,固化结束后靠近线轴的初始缠绕层应变较大;由于光纤缠绕退匝而形成的线包两端厚度减小,沿轴向呈现出由中间向两端逐渐变大的应变分布特征;线包内部都存在明显不均匀的残余应力。
3)固化变形会随着固化温度升高而增大,随着线包缠绕层数变大,线包等效残余应力在变大,但线包最大变形量却随着线包厚度的增大而变小。
