移动机器人优先采样D3QN路径规划方法研究

袁 帅,张莉莉,顾琦然,张 凤,吕佳琪

1(沈阳建筑大学 信息与控制工程学院,沈阳 110168) 2(中国科学院 沈阳自动化研究所,沈阳 110016)

1 引 言

路径规划是指机器人可以在不碰撞的情况下从初始位置移动到目标位置规划最优路径.传统的路径方法是将路径规划问题转化为搜索或最优问题,其缺点是较为依赖先验知识,实时性和灵活性不高,并不适用未知环境.强化学习基于马尔可夫决策过程(Markov Decision Process,MDP),通过与环境不断交互学习和训练的方式,规划出移动机器人的实时路径.将深度学习(Deep Learning,DL)和强化学习(Deep Learning,DL)各自的优势相结合就是深度强化学习(Deep Reinforcement Learning,DRL),其中深度学习对高维状态空间进行特征提取,与环境不断交互,强化学习对移动机器人的决策控制,既满足机器人的移动要求又解决大规模环境下的规划问题,且DRL已逐渐成为实现室内机器人路径规划的方案之一[1].

深度强化学习最初在游戏仿真领域应用,后来逐渐应用于机器人导航、调度与优化等领域,被认为是人工智能(Artificial General Intelligence,AGI)的重要方向之一.DeepMind于2013年提出了深度Q网络(DeepQ-Network,DQN),将CNN与Q-learning结合提出端到端的控制策略模型,在Atari 游戏中进行完美验证[2].2015年再次提出Nature DQN 算法,因出色的表现奠定其地位,深度强化学习的研究热潮正式开始[3].

在移动机器人路径规划领域应用最为广泛的深度强化学习算法是DQN算法.传统的DQN算法存在以下问题:1)过估计问题,即动作选择和计算Q值采用同一网络模型参数,导致选择过高的估计值,获取不太精确的Q值函数,出现过多的无效迭代训练过程,降低训练速度;2)样本利用率低,即在回放经验池中进行重采样数据训练,原本的随机采样机制会导致训练样本种类比较单一,进而导致移动机器人对环境探索率较低,易获取局部最优解,降低训练速度.

针对以上问题,很多学者提出了各种基于DQN的改进算法.文献[4]提出了基于动态融合目标的DTDQN方法,将DQN与Sarsa算法的思想结合,有效地解决了值函数过估计问题,提高训练速度.文献[5]提出了利用原始图像获取最优动作,解决了过估计问题,保证机器人能够避障到达目标位置;文献[6]提出一个更正函数对评价函数进行改进,使得最优Q值与非最优Q值的差异增大,减少过估计的影响;文献[7]提出一种探索噪音的EN-DQN方法,加入改进的LSTM单元,该算法大大提高了机器人的训练速度;文献[8]基于DDQN方法,利用压缩的全局环境地图与代理附近的裁剪但未压缩的局部地图相结合,该算法提高了训练速度.文献[9]提出一种动态实时融合的DDQN方法,通过先验知识和调整权重进行网络参数训练,减少过估计来保证所选策略最优.文献[10]提出动态目标 DTDDQN的算法,将 DDQN与平均 DQN 算法相结合,改进网络参数,解决了过估计的问题.

对于样本利用较低的问题,文献[11]将深度图像作为输入,将继承特征的导航策略迁移到未知环境中,提高样本利用率;文献[12]提出了样本存储的DQN方法,利用回放池存储网络数据来解决采样效率低的问题,并通过仿真环境和真实环境分析验证了算法的有效性;文献[13]提出二次主动采样方法,从序列累积回报和TD-error两部分选择样本,用两次采样得到的样本训练获取最优策略;文献[14]提出了状态值再利用的RSV-Dueling DQN方法,将奖励值标准化后再与 Dueling-DQN 得到的Q值进行结合,提高了样本利用率.文献[15]提出一种改进NDQN方法,加入了差值增长概念,利用改正函数提高样本利用率;文献[16]提出了一种改进的DQN算法,创建一个体验价值评价网络,利用并行结构增大对其他点的探索,提高样本的利用率.文献[17]提出一种结合LSTM强化学习路径规划算法.以环境图像作为输入,利用自动编码器对环境图像特征降维,降低了模型的复杂程度,提高了算法稳定性.上述对DQN算法的改进在一定程度上提高了算法性能,但是依然存在因样本数据过大而导致收敛速度过慢的问题.

针对以上问题,本文提出D3QN-PER端到端模型的路径规划方法.首先,在模型感知端上加入LSTM,将障碍物状态向量输入到 LSTM 网络,采用遗忘门选择障碍物的关键信息;然后,采用优先经验回放机制,抽取有利的样本进行训练.最后验证算法,通过Gym-breakout游戏测试进行初步测验,再采用Ros-Gazebo平台设置3个不同复杂程度的仿真环境依次进行训练,分别对D3QN-PER、D3QN、DDQN、DQN这4种算法进行比较,实验结果表明D3QN-PER算法与其他3种方法相比,收敛速度和到达目标点成功率P均得到大幅度提升,可证明该方法在未知环境中可以更好地获取最优路径,对未知环境的路径规划具有一定研究意义.

2 深度强化学习方法

2.1 Double DQN

DRL 是一种通用性的感知与控制系统.Q-learning的更新公式为:

(1)

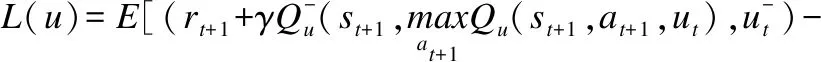
(2)

2.2 Dueling DQN

机器人通过观测获得环境数据,将环境数据作为输入数据,先通过神经网络对数据进行分析,在当前网络中输出最大Q值,目标网络中输出最优动作Q值,因为重复计算最优动作的Q值,易产生奖励偏置问题(reward-bias),因此利用Dueling DQN[19]的思想,引入竞争网络,分别平衡当前网络和目标网络中动作对Q值的影响,去除奖励偏差,最后输出每个动作的Q值,竞争网络Q值计算公式如下:

Q(s,a;θ,ϑ,β)=νη(fξ(s))+

(3)

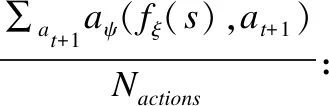
3 D3QN-PER算法

本文采用基于D3QN-PER的路径规划算法.如图1所示为D3QN-PER模型结构.

如图2移动机器人路径规划流程所示.将激光传感器收集障碍物So送入模型感知端的LSTM中提取障碍物特征,转换同维度的向量和机器人状态Sr输入至D3QN-PER网络中,计算Q值得到当前动作A,并根据获取的奖励R评估动作A的好坏.机器人进入下一个状态,并将当前数(s,s′,a,r)存储到缓存回放池中,通过小批量数据进行优先重要性采样训练,循环迭代更新网络参数,直至训练完成,通过不断循环以上过程,以累积奖励值reward最大化为目标,直至得到最优动作值函数Q*(s,a)对应的最优动作.

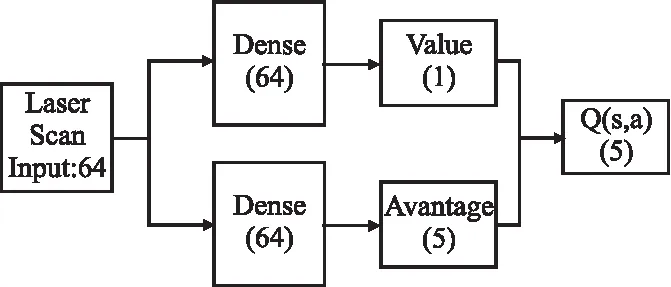
图1 D3QN-PER模型结构Fig.1 D3QN-PER model structure diagram

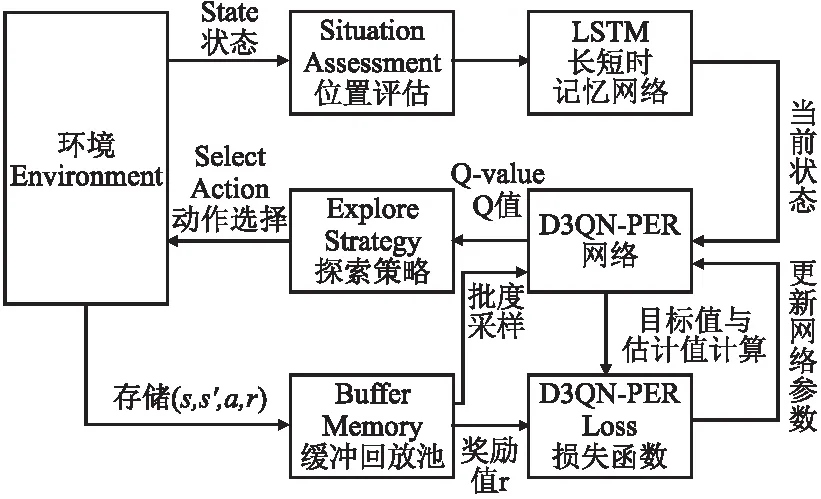
图2 移动机器人路径规划流程Fig.2 Flow chart of mobile robot path planning

3.1 长短时记忆网络

强化学习可视为无后效性的马尔可夫过程,即系统的当前状态只与前一时刻状态有关,而与更早的状态无关.长短时记忆网络(Long Short Term, LSTM)是一种循环网络结构,使机器人具有长期记忆功能,接受任意长度的序列输出固定大小向量.如图3 LSTM处理模型图所示,因此把障碍物信息So看作是一个输入序列,在每一个决策步骤中,将每一个障碍物状态S输入一个LSTM单元,LSTM最初处于空状态,接受So1经过遗忘门提取关键信息,存储在h1,依此类推.当移动机器人的障碍物信息So被输入时,使用h存储相关信息,并舍弃不太重要的部分.在输入所有障碍物的状态信息后,可以将存储在LSTM状态信息的维度转换为统一维度的状态向量So,用于之后的决策控制.障碍物状态So作为输入数据,经过LSTM网络处理后,得到统一大小的障碍物状态So,再和移动机器人自身状态Sr结合,输送到D3QN网络的输入端,经过全连接层等处理,最后输出状态空间和离散动作空间组成的动作值函数Q(s,a).

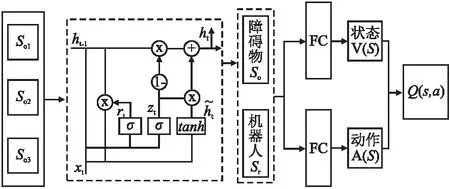
图3 LSTM处理模型图Fig.3 LSTM processing model diagram

图3中的虚线部分是LSTM的内部结构.LSTM利用3个“门”机制决定信息的去留.丢弃的信息由遗忘门确定,读取上一个LSTM单元的输出ht-1和当前LSTM单元的输入xt,通过sigmoid激活函数过滤的信息输出到ft.输入门存放过滤后的新信息,sigmoid函数更新信息it;输出门利用tanh激活函数输出候选值向量mt;新信息it×mt加上历史状态的细胞ct-1×ft完成细胞更新.输出门输出ht值,首先sigmoid函数输出ot,再与tanh函数输出的ct相乘,输出ht.LSTM各单元门的工作原理如式(4)～式(7)所示:

zt=σ(Wz·[ht-1,xt])

(4)

rt=σ(Wr·[ht-1,xt])

(5)

(6)

(7)

3.2 优先经验回放机制

由于使用均匀采样方法无法区分样本的重要性,经验回放池的内存有限,造成采样低效性.因此对学习帮助的数据增加采样频率,学习无帮助的数据减少采样频率,提高学习效率.本文提出基于时间差分误差(TD-error)改进的优先经验回放机制.时间差分误差计算如公式如下:

(8)

εj是DQN网络中的时间差分误差,将最近的时间差分误差绝对值作为历史经验轨迹进行采样的概率P,时间差分误差越大,预测精度的上升空间就越大,表明基于该样本的学习能够获得更好的提升效果,其优先级P应越高.

(9)

当α决定使用优先级,α=0是均匀随机采样.基于比例优先级采样的公式如下,其中参数σ防止出现缓存采样记忆单元概率为0的情况.

Pj=|εj|+σ

(10)

基于均匀采样公式如式(11)所示,一般转移样本的重要性与样本采样的概率,即超参数ω决定概率分布情况.

(11)

(12)

ωi为转移样本i的权重,β用于调节偏差程度.该机制通过调节权重ω的大小保证优先更新重要性高的转移样本,以一定概率更新重要性较低的转移样本同时保证样本的多样性,提高网络的训练效率.

4 实验结果及分析

4.1 基本环境

强化学习最初利用游戏仿真验证其学习性能.因此,本文搭建Gym平台中breakout游戏环境.对DQN、DDQN、D3QN、D3QN-PER方法分别比较,验证其学习性能.配置是TensorflowGPU1.15、Python3.6、OpenCV4.5等.

4.1.1 breakout游戏环境

在游戏环境中,挡板在屏幕范围内可以向左或右移动.其中累积消除的砖块越多,分数越高,即代表算法的学习性能越好.

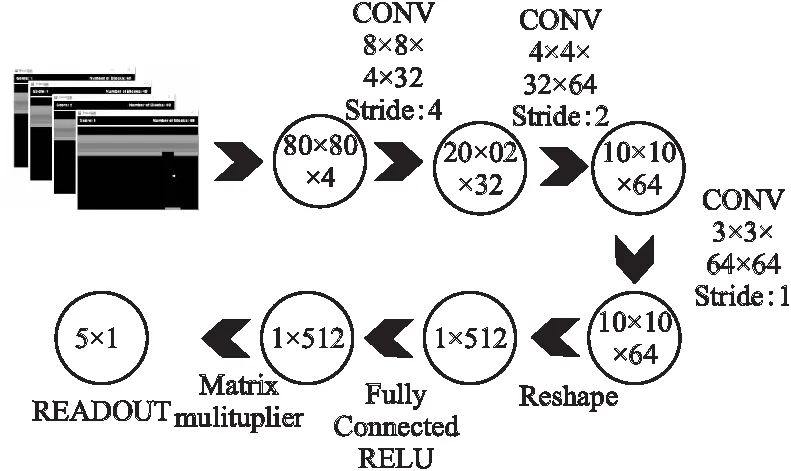
图4 卷积神经网络图Fig.4 Convolutional neural network diagram

如图4卷积神经网络图,首先将预处理后连续4帧的80×80的灰度图像作为神经网络的输入,感知游戏环境的动态性,经过3层卷积层处理输出10×10×64的特征张量,经过reshape成为1×512的一维向量,经过全连接层最终输出5个神经元即输出值的大小对应不同动作的Q值.

4.1.2 结果与分析

如图5所示,可以看出D3QN-PER方法与其余3种算法相比,收敛速度较快.如图 6所示,可以看出D3QN-PER的AverageScore明显高过其余3种方法,其AverageScore是DQN算法的2倍.一般来说,收敛速度越快,其对应机器人在更少迭代次数学习性能越好;平均累积奖励值越多,其对应机器人到达目标点的次数越多;因此,表明D3QN-PER算法具有更好的学习能力,能更快更好地在未知环境中获取最优路径.

图5 Breakout游戏仿真平均损失函数值Fig.5 Breakout game simulation average loss function value

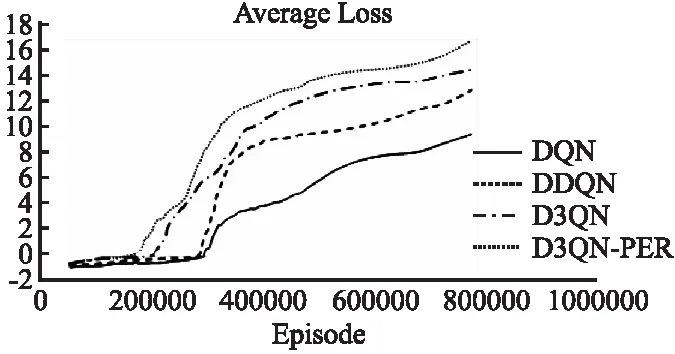
图6 Breakout游戏仿真平均奖励值Fig.6 Breakout game simulation average reward value

评价指标是平均累积奖励AverageScore,平均损失函数值AverageLoss.实验参数在表1中给出.

(13)

(14)

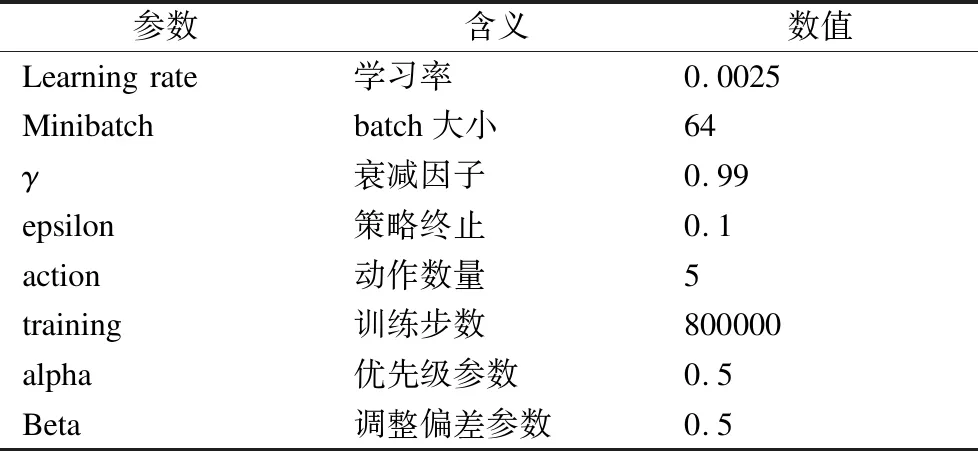
表1 Breakout游戏仿真实验参数

4.2 仿真实验

仿真实验:因为深度强化学习需要大量训练数据,实际实验中可能对硬件设备有损坏,因此大多数采用仿真环境训练的.本文使用稀疏激光测距结果作为输入,以减少机器人在仿真世界和现实之间的可观察差异.

实验环境为TensorFlow框架,Python3.6,Gazebo7.0,使用Turtlebot3 burger双轮机器人在ROS-Gazebo搭建仿真环境中进行训练.Turtlebot3 burger 机器人根据在移动过程中获得实时位置,通过与实时位置的距离判断当前状态,将激光传感器收集到坐标数据作为输入,输出相应动作,通过激光测距传感器来实现路径规划.设置的动作空间包括5个动作:向前移动,向右或向右转动,向左或向左转动.

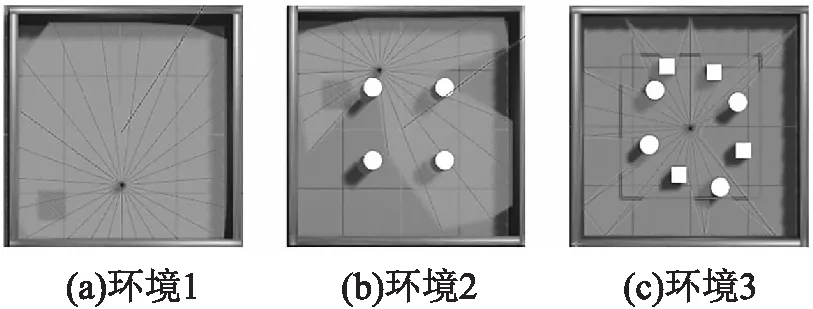
图7 仿真环境1-3Fig.7 Simulation environment 1-3

首先构建了3个复杂程度不同的室内环境进行训练,验证D3QN-PER和DQN、DDQN、D3QN4种算法的性能.如图7所示,3个不同仿真实验环境,环境的复杂程度依次递增,实验环境1有四面墙封闭无障碍物的环境,首先移动机器人进行训练,让其具备到达目标点和躲避墙壁障碍的能力.实验环境2是在环境1的基础上加入4个位置相对规律的圆柱体障碍物,训练机器人具备躲避静态障碍物的能力.实验环境3是在环境2的基础上增加4个的正方体障碍物,这些障碍物分布密集且没有规律,加大了移动机器人路径规划的难度,可以进一步验证算法性能.本实验中使用机器人是Turtlebot3中burger双轮机器人,使用稀疏24维的激光测距结果和相对目标位置来完成路径规划任务,而不会发生碰撞.在每次回合更新时,目标位置在整个区域内随机初始化,并且与障碍物的位置不相同.

D3QN-PER 方法参数设置如表 2所示,其中探索因子ε范围在(0.1,1)线性递减.神经网络中采用均方根的随机梯度下降方法更新参数,每次从回放池中抽mini-batch=64的样本更新网络.

表2 仿真环境1-3实验参数Table 2 Simulation environment 1-3 experimental parameters

奖励值函数设置如下所示:

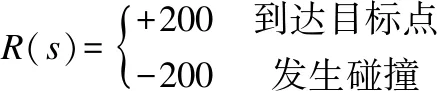
(15)

奖励函数设置包括正负奖励,目标点设置为单位为1的红色正方形,安全距离阈值为0.2m,移动机器人在安全距离阈值范围到达目标位置,可认定是到达目标位置,获取正向奖励值+200,一直训练直至超时或发生碰撞,进入下一回合;障碍物设置为尺寸统一的圆柱体、正方体,及可拟作为实际环境中墙壁的四面正方形板,碰撞检测阈值为0.4m,移动机器人在碰撞检测阈值范围内碰撞障碍物,可认定移动机器人发生碰撞,获取负向奖励值-200,本回合结束,进入下一回合继续训练,直至所有回合数训练完成.

结果和分析如下所示:

1)仿真环境1仿真分析

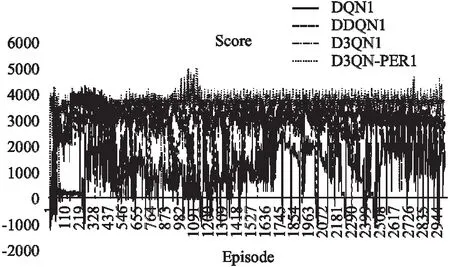
图8 仿真环境1累积奖励值Fig.8 Simulation environment 1 cumulative reward value

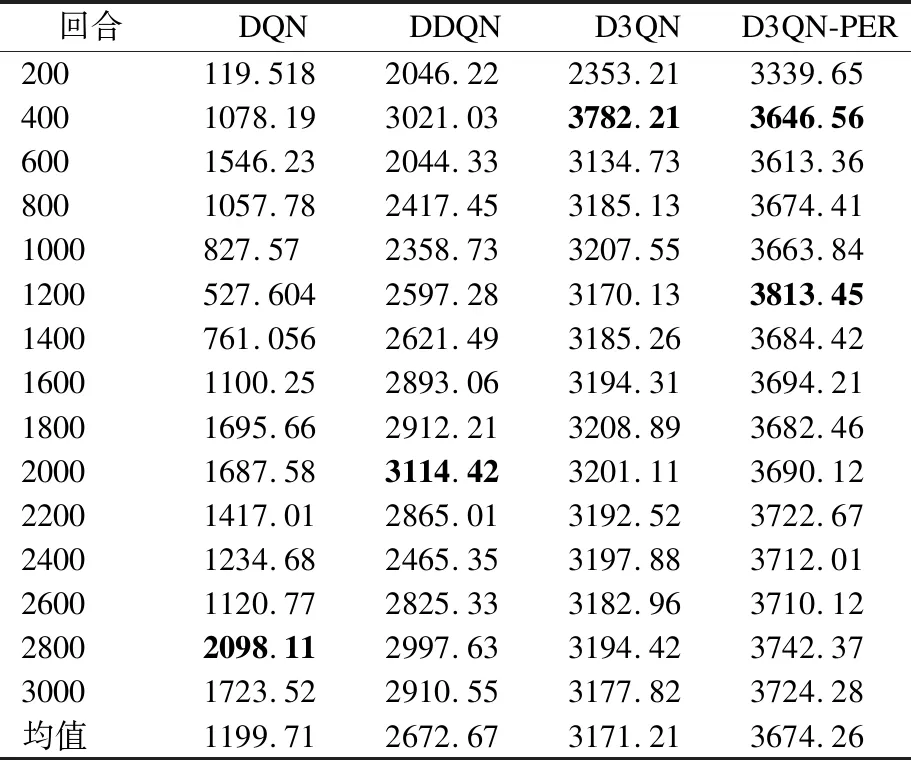
表3 仿真环境1的平均累积奖励值Table 3 Average cumulative reward value of simulation environment 1

图8展示的是DQN、DDQN、D3QN、D3QN-PER这4种算法的累积奖励值图,可以明显看出,D3QN-PER的累积奖励值比较稳定,而DQN、DDQN、D3QN算法的波动性较大,尤其DQN算法波动频繁.

在表3中,看出4种算法平均累积奖励值在3000次回合中均为正数,且稳定变化,DQN算法在2600～2800回合为最高值2098.11,DDQN算法在1800～2000回合为最高值3114.42;D3QN算法在200～400回合为最高值3782.21;D3QN-PER在1001～1200回合为最高值3813.45,是 DQN 算法平均累积奖赏值的1.8倍,这表示 D3QN-PER 方法在较少的迭代次数就完成了移动机器人在仿真环境1中路径规划的训练.

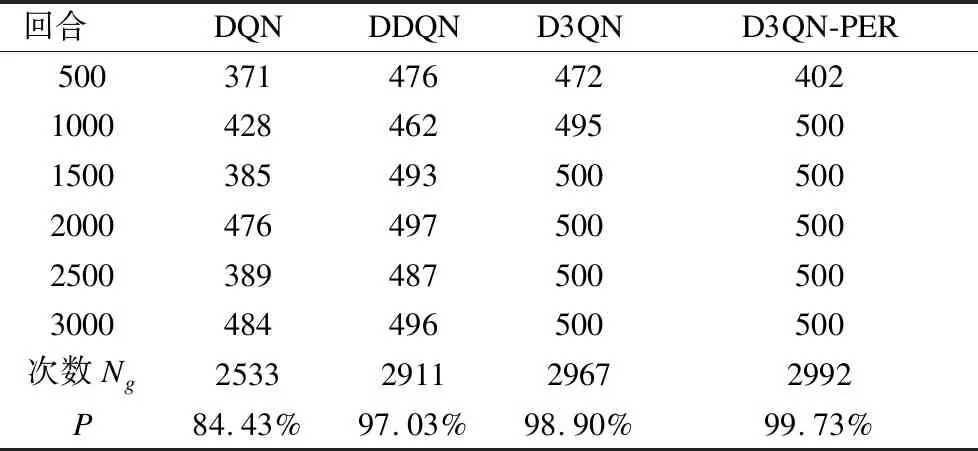
表4 仿真环境1到达目标点次数Table 4 Simulation environment 1 number of times to reach the target point

一般移动机器人进行训练时,获取正向奖赏值越多,对应在路径规划过程中,代表能成功避开障碍物到达更多目标点次数越多,其获取的路径越接近于最优.将到达目标点的成功率P作为一个验证指标.

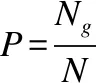
(16)

Ng:3000回合中成功到达目标点次数

N:代表总的训练回合次数,即N=3000

如表4所示,可以明显看出D3QN-PER算法成功到达目标点次数最多,为2992次,并且D3QN-PER 方法的到达目标点的成功率P比 DQN 算法提高了1.2倍多.

2)环境2的对比实验数据图

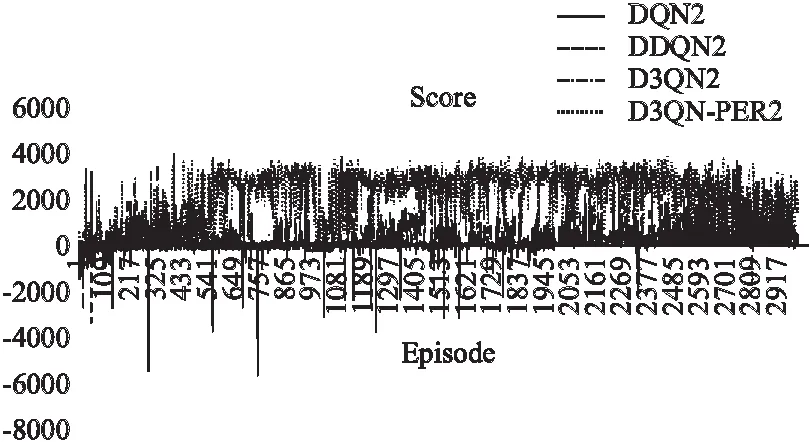
图9 仿真环境2累积奖励值Fig.9 Simulation environment 2 cumulative reward value

从图9中可以看出,DQN算法的累积奖励值在正负值波动,其余3种算法的累积奖励值在正值范围波动,且它们的累积奖励值呈逐渐上升趋势.

如表5中所示,明显看出DQN算法在前期出现负值,后期出现正值,在2400～2600回合为最高值113.12;DDQN算法偶尔出现负值,在2800～3000回合为最高值219.27;D3QN算法全部为正值,且在1400～1600回合为最高值749.51,与DQN、DDQN算法相比,训练效果大大提升;而D3QN-PER算法不仅全部为正值,且最高值远远大于D3QN回合最高值,说明D3QN-PER效果比D3QN效果更加稳定,这表示D3QN-PER方法通过较少的迭代次数就完成了移动机器人在仿真环境2中路径规划的训练.

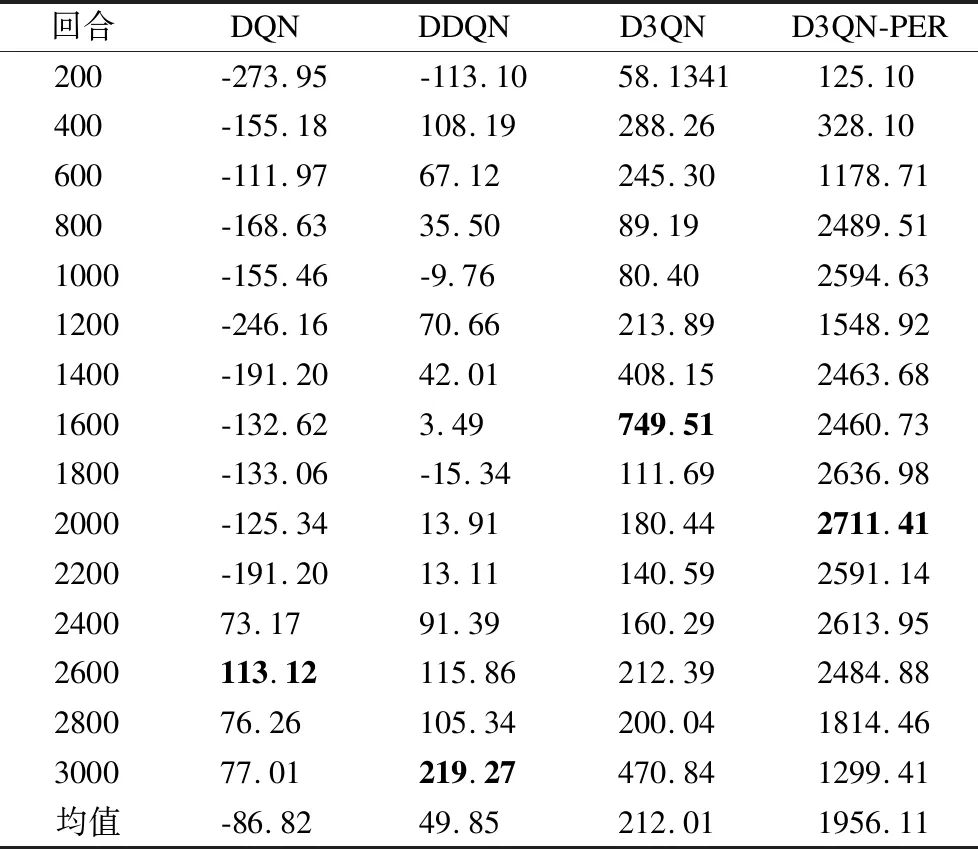
表5 仿真环境2的平均累积奖励值Table 5 Average cumulative reward value of simulation environment 2

如表6所示,和仿真环境1的数据对比,明显看出DQN、DDQN、D3QN、D3QN-PER这4种算法的成功到达目标点次数Ng差距很大,其中D3QN-PER算法成功到达目标点次数为2112次,DQN算法成功到达目标点次数为142,DDQN算法成功到达目标点次数为472,D3QN算法成功到达目标点次数为1150,D3QN-PER算法的成功率P比 DQN 算法提高了15倍多,可证明D3QN-PER 算法在仿真环境2中训练效果最佳,即能在仿真环境2中获取最优路径.

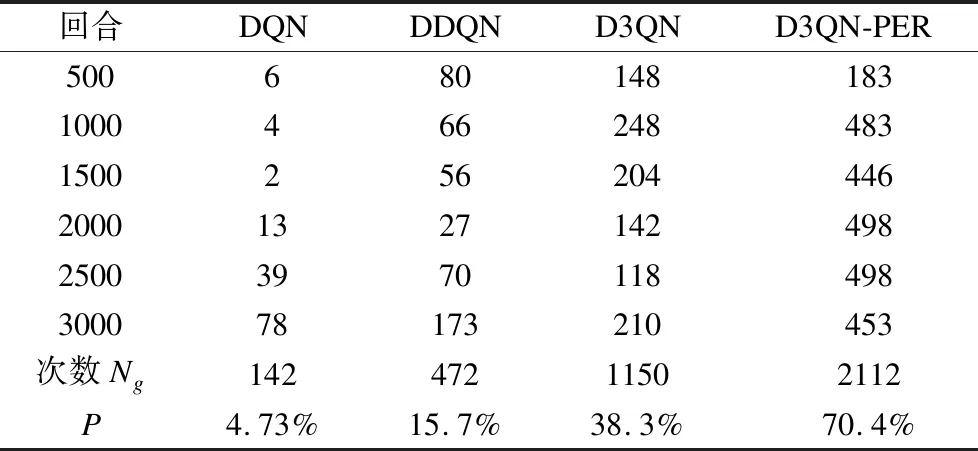
表6 仿真环境2 到达目标点次数

3)环境3仿真分析

图10 仿真环境3 累积奖励值Fig.10 Simulation environment 3 cumulative reward value

从图10中可以看出,DQN、DDQN算法的累积奖励值在负值范围波动,而D3QN、D3QN-PER算法均在正值范围内波动,而且D3QN-PER算法的累积奖励值呈大幅度上升趋势.

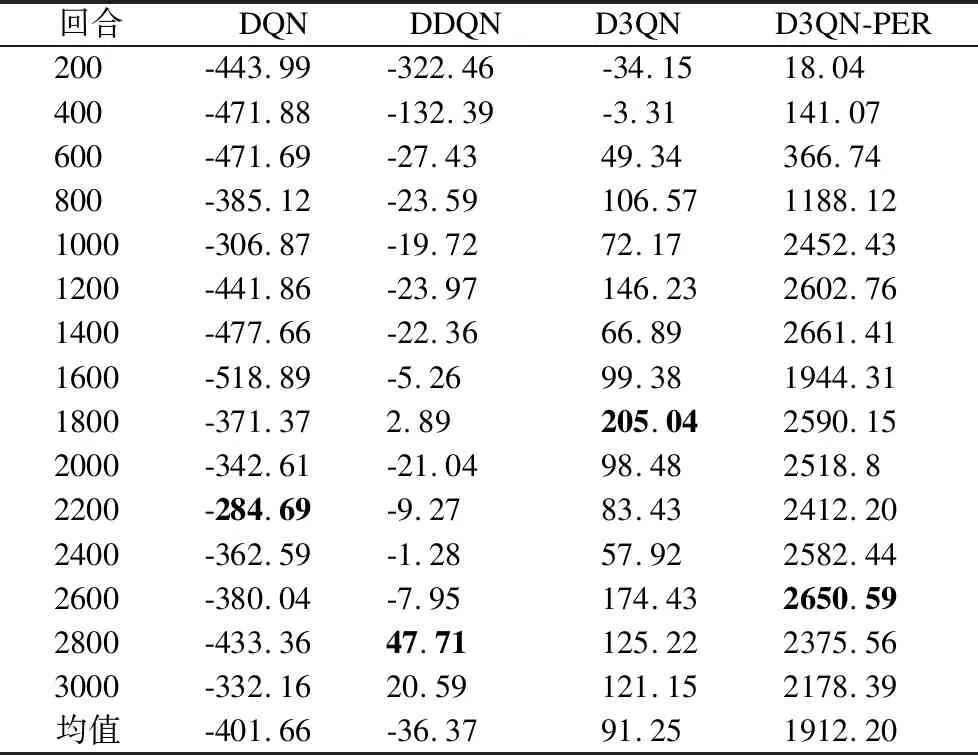
表7 仿真环境3 的平均累积奖励值

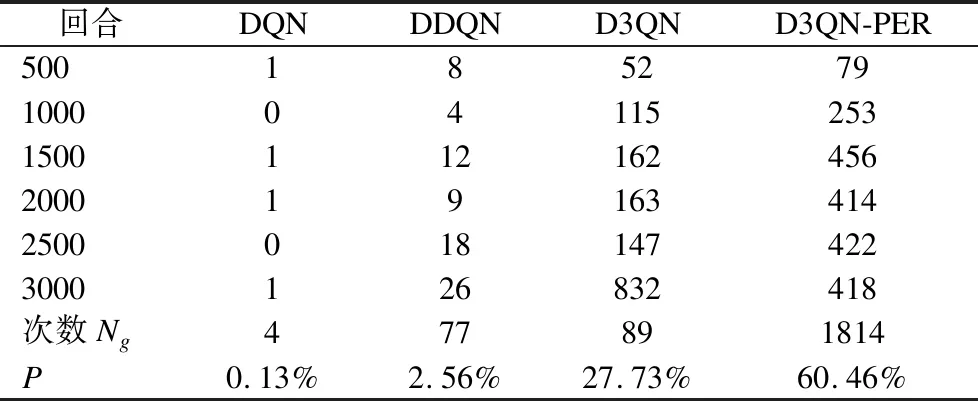
表8 仿真环境3到达目标点次数

如表7中所示,明显看出DQN的平均累积奖赏值均为负值,说明机器人没有成功到达目标点位置无法获取最优路径;DDQN算法只在2601～2800回合为最高值,值为47.71,其余大部分为负值;D3QN在早期出现负值,后期出现正值,在1601～1800回合为最高值205.04,与DQN、DDQN算法相比,训练效果大大提升,依旧会发生碰撞;D3QN-PER均为正值,在2401～2600回合为最高值2650.59,因为DQN、DDQN算法在3000回合的总平均累积奖励值均为负值,说明DQN和DDQN算法对于复杂度较高的仿真环境3并不适用,D3QN算法效果也不如D3QN-PER的效果稳定,这表示 D3QN-PER 方法通过较少的迭代次数就完成了移动机器人在仿真环境3中路径规划的训练.

在表8中,可以明显看出D3QN-PER算法在3000次回合中成功到达目标点次数最多,累积次数为1814次,其到达目标点的成功率P远远高于其余方法.

对上述结果分析,仿真环境情况越复杂,D3QN-PER算法效果越明显,移动机器人所需要的训练时间更少,提高了移动机器人的学习性能.

5 结 论

本文针对未知的室内场景,在传统DQN算法的基础上,提出了D3QN-PER模型.D3QN-PER模型利用D3QN模型解决如何获取精确Q值的问题;使用 LSTM处理激光传感器信息,使模型具有提取和记忆障碍信息功能.动作和奖励的历史信息被当作Q值网络的输入,提供更完整环境的信息.利用稀疏激光测距作为输入,减小仿真环境与现实之间的差异,训练后的模型适用于真实环境中的机器人,从而提高了移动机器人自主决策和自主学习的能力.通过Gym中Breakout游戏验证D3QN-PER的学习性能,然后通过Ros-Gazebo搭建3个复杂程度不同仿真环境,从简单到复杂依次对DQN、DDQN、D3QN、D3QN-PER进行路径规划的训练,实验结果表明,对于简单的仿真环境1,4种算法学习性能相差不大;对于难度增加的仿真环境2,D3QN-PER算法的学习性能相当于传统DQN算法的2倍;对于最为复杂的仿真环境3,D3QN-PER算法的学习性能,远远高于其余3种算法,D3QN-PER 方法明显提高了移动机器人的学习速度,同时验证了该方法对不同环境的适应性,该方法对于移动机器人在未知环境的路径规划比经典的DQN算法更有效、更稳定.