基于碳循环优化算法的船舶航路规划方法

宋冬宇 陈顺怀 罗 亮 郑 龙 杨 达

(武汉理工大学船海与动力工程学院1) 武汉 430063) (高性能船舶技术教育部重点实验室2) 武汉 430063)

0 引 言

船舶智能航路规划是船舶实现智能化航行的关键技术之一[1].船舶智能航路规划的主要任务是根据船舶航行时所经过的水域环境情况,按照一定的策略自动寻找一条或多条从起点到终点的可航行路线.目前,国内外学者基于不同的环境建模方法采用各异的智能优化算法对船舶智能航线规划问题进行相关探索.文献[2]基于海图栅格模型将船舶路径规划转化为多目标优化问题应用改进NSGA-III算法求解得到多条可航路线.文献[3]将势场合力与距离信息结合改进了传统蚁群算法的启发函数,并通过仿真实验证明了改进蚁群算法能够提高船舶航行路径的全局搜索能力.文献[4]将遗传算法与非线性规划方法相结合提出混合遗传算法针对不同会遇态势下船舶路径规划问题进行了有效的求解.文献[5]结合人工势场思想改进通航环境模型,提出A*改进搜索步长及搜索方向限制解决风电场区风机维护船舶路径规划问题.综上所述,智能优化算法用于解决路径规划问题是船舶智能航行路径规划的研究方向,由于传统优化算法有过早收敛,容易陷入局部最优,难以兼顾多个优化目标的缺点,因此需要对传统算法进行改进或探索新的优化算法.

碳循环智能优化算法(carbon cycle optimization algorithm,CCA)是一种模拟碳元素在生物圈与大气圈中交换循环的智能优化算法,该算法具有全局搜索能力强、收敛速度快的优点,在解决小范围多目标优化问题时有一定的优势.文中通过几何图法进行环境建模采用一维编码方式,考虑航行安全性、路线平滑程度和航行总距离,结合碳循环优化算法解决船舶智能航行路径规划问题,并通过仿真实验验证了本文方法的可行性.

1 问题描述及模型建立

1.1 船舶路径规划问题描述

船舶全局航行路径规划问题是在环境信息已知的条件下寻找到可航行的路线.在进行规划时一般仅考虑静态障碍物,包括大陆、岛屿、岩石等位置固定不动的障碍物.静态障碍物信息可在进行航行规划前读取海图数据获取.

在船舶路径规划过程中需要对路径搜索问题设定优化目标.路径平滑程度与船舶操纵性相关,船舶在航行时进行大角度转弯时会造成船体倾斜影响船体稳定性同时转路径不平滑也会造成航行时间增加.航行总距离关系燃料消耗和碳排放对船舶航行成本和绿色性有重要影响.因此,将航行安全性,路线平滑程度和航行总距离作为优化目标对船舶路径搜索问题进行求解.

1.2 通航环境模型建立

环境建模采用最多的方法为栅格法及几何图法,栅格图法建模时障碍物的表达依赖于栅格的大小,栅格过大不能准确表达障碍物信息,栅格过小会增加搜索时间不利于大范围水域的路径规划.因此,环境建模时采用几何图法将障碍物抽象表示为几何图形,采用几何图法建模时会导致航线紧挨障碍物边界,然而船舶在紧挨障碍物行驶时往往吃水不能达到航行要求并且船舶本身具有一定的体积在紧挨障碍物行驶时容易发生碰撞,因此需要对障碍物进行膨胀化处理.障碍物表达示意图见图1.

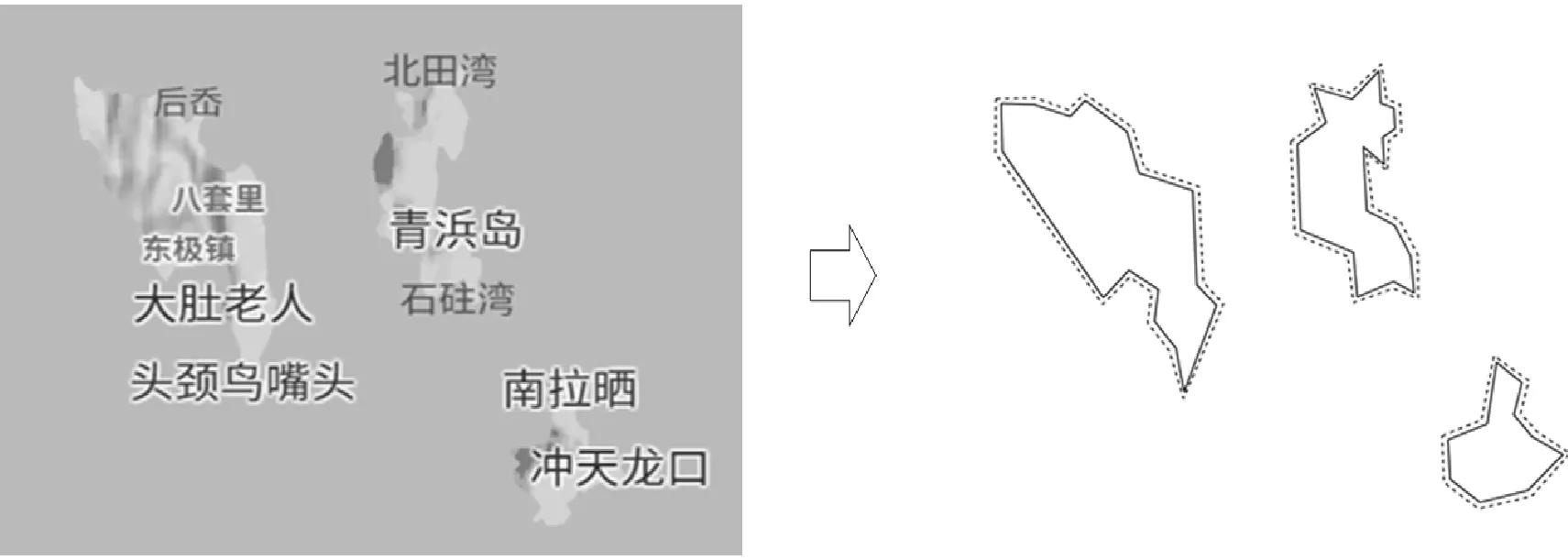
图1 障碍物表达

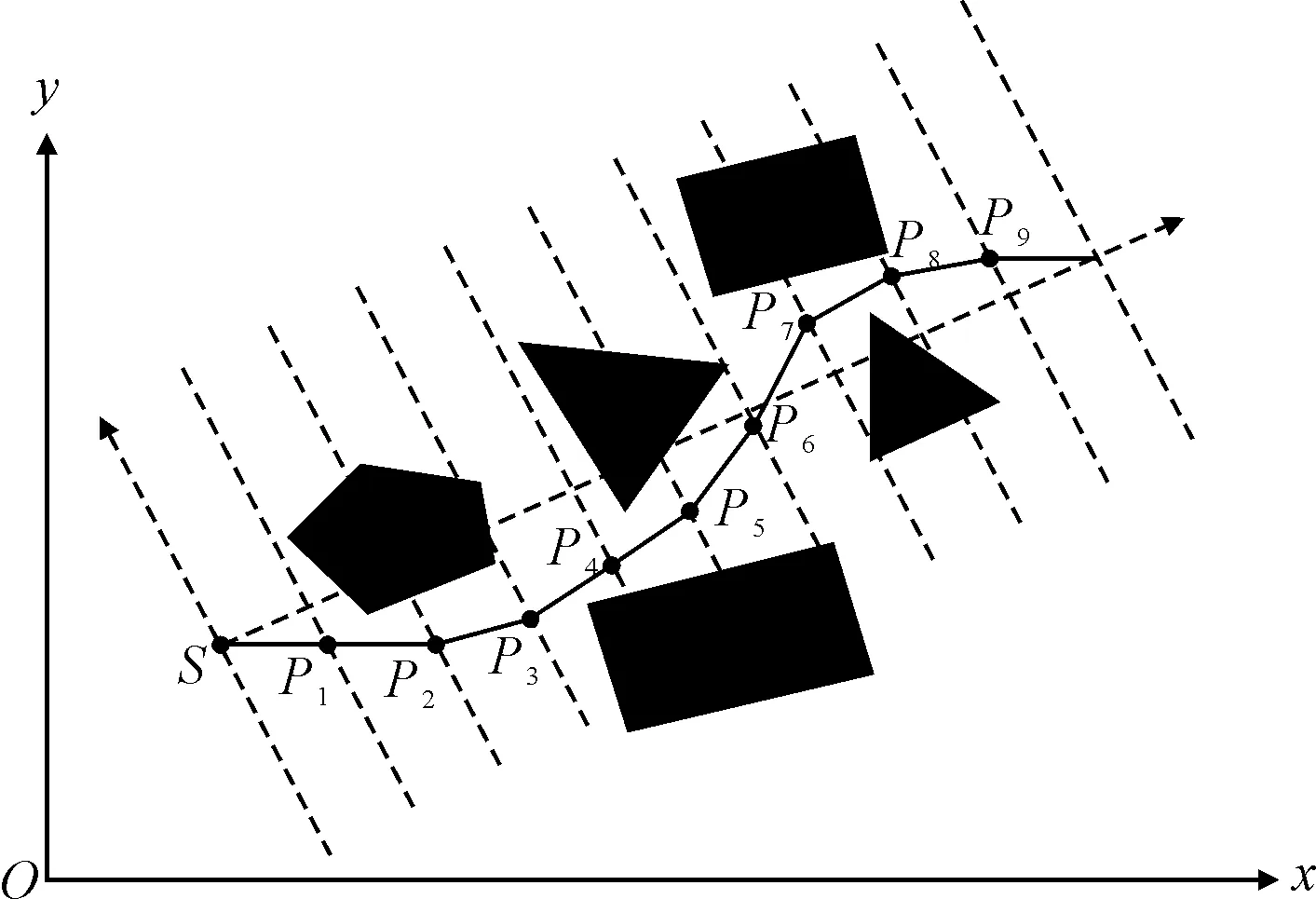
图2 路径编码方式

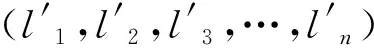
路径点集编码时需要将障碍物边界点坐标以及起点终点坐标进行转换,转换公式为

(1)

式中:(x,y),(x′,y′)分为任意Pi在原始坐标系O-xy和新坐标系O-x′y′下的坐标;θ为坐标轴x与直线SG之间的夹角,由x轴转向直线SG,逆时针方向为正;(xs,ys)为起点S在原始坐标系O-xy下的坐标.在新坐标系下优化得到路径途径点集后需通过式(2)反变化到初始坐标系下的坐标.

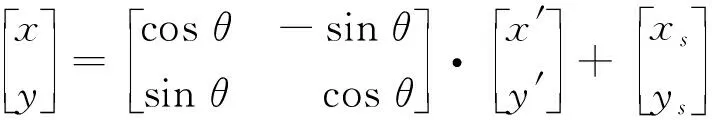
(2)

1.3 路径搜索模型建立

考虑航行安全性、路线平滑程度和航行总距离三个优化目标.优化目标函数设定为

minf(R)=w1×Safety(R)+w2×

Smoothness(R)+w3×Length(R)

(3)

式中:w1,w2,w3为权值;Safety(R)为规划路径的安全程度;Smoothness(R)为规划路径的平滑程度;Length(R)为规划路径的长度,分别定义为

(4)

式中:Penal为惩罚值;Collision(PiPi+1)为航段PiPi+1与障碍物的碰撞次数

(5)

φ(Pi)=π-

(6)

式中:φ(Pi)为船舶在该途径点处的转向角度;d(PiPi+1)为路径点PiPi+1间的欧式距离.

(7)

2 碳循环优化算法及其性能分析

2.1 碳循环优化算法

碳循环是碳元素在地球的岩石圈、岩石圈、水圈和大气圈中交换的现象,并随着地球的运动不断循环.在碳循环算法中,模拟了生物圈和大气圈之间碳元素的循环,示意图见图3.

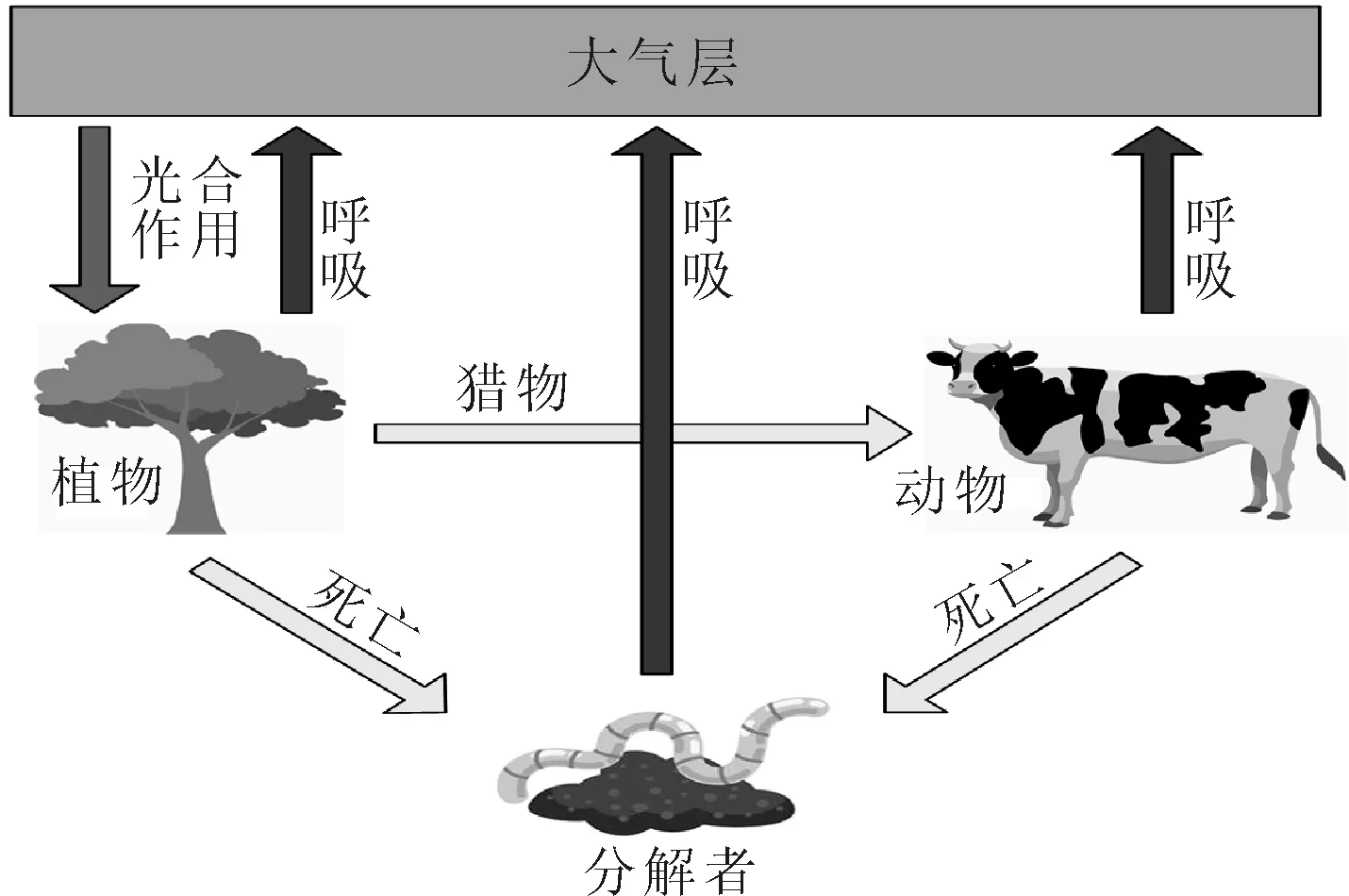
图3 碳循环过程

根据碳循环过程将优化算法主要分为五个阶段:动植物呼吸、动物捕食、动植物死亡、微生物分解以及植物光合作用.

2.1.1动植物呼吸

在碳循环过程开始时,碳元素以含碳有机物的形式存在于动植物体内,其中部分含碳有机物被用于动植物呼吸作用.动植物通过呼吸作用中的逐步反应将这部分含碳有机物分解为体积更小,结构更简单的含碳无机物(主要为二氧化碳)释放到大气中,大气中的碳元素位置分布具有随机性.该过程的数学模型为

(8)

(9)

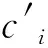
2.1.2动物捕食

在碳循环算法中,将动物捕食阶段根据碳元素的转移过程进行简化,在该阶段只考虑动植物之间的捕食过程不考虑动物间的捕食过程.在呼吸阶段植物中部分碳元素由于呼吸作用由含碳有机物转化为二氧化碳回到大气圈中,在动物捕食阶段,剩余以含碳机物形式存在于植物中碳元素将通过动物捕食行为部分转移到动物体内以含碳有机物的形式继续存在.该过程的数学模型为

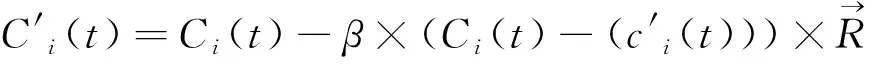
(10)

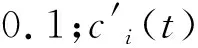
2.1.3动植物死亡

在碳循环过程中,动植物死亡的过程可视为将体内含碳有机物向分解者转移的过程.同时,动植物死亡与时间直接相关,因此随着算法循环迭代碳元素的转移会发生改变.

(11)

(12)

(13)

式中:maxt为最大迭代次数;tnow为当前迭代次数;f为控制系数,一般设为1.5,随着迭代次数的增加γ从f线性下降到0.

2.1.4微生物分解

在动植物死亡后,体内留存的含碳有机物通过微生物的分解作用被分解为二氧化碳并将其释放到大气圈中,该过程使得生物圈中的碳元素重新回到大气圈中.分解过程数学模型为

(14)

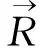
2.1.5植物光合作用

大气中的碳元素主要通过植物进行光合过程进入生物圈,在现实生活中通常希望植物吸收更多的二氧化碳优化环境质量.植物通常贴近地表,在吸收大气中二氧化碳时通常选择靠近自身位置的二氧化碳分子,因此通过评价函数找出适应度更好即更靠近自身位置的碳元素进行光合作用.该过程使得大气圈中碳元素进入到生物圈中.其数学模型为

(15)

在碳循环算法中,植物光合作用时对大气中的二氧化碳分子应用适应度函数进行评估,选择适应度最好即位置最靠近自身的二氧化碳分子作为植物光合作用合成含碳有机物的原料.

2.2 算法测试实验

2.2.1测试实验一

在实验一中使用的测试函数在表1中提供,相对应的函数图像见图4,所有函数的维度均为30.将碳循环算法的结果与四种典型的优化算法进行了比较,这四种算法分别是PSO算法,GA算法,GWO算法和ALO算法,PSO和GA的结果通过Matlab 2019a中的PSO和GA工具箱进行计算.本实验中使用的ALO和GWO算法的源代码下载于http://www.alimirjalili.com/ALO.html 和http://www.alimir-jalili.com/GWO.html.对于PSO、GA、ALO和GWO,种群规模为30,最大运算次数为1 000;对于CCA,碳元素规模大小等于30,最大迭代次数为1 000.所有考虑的算法在每个基准函数上独立运行30次.统计结果(ave和std)见表2.

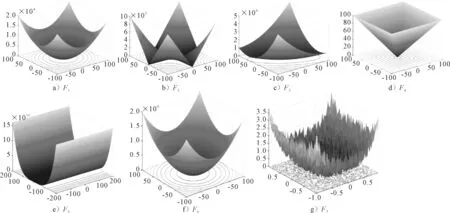
图4 单峰测试函数对应的函数图像

表1 单峰基础测试函数

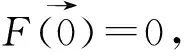
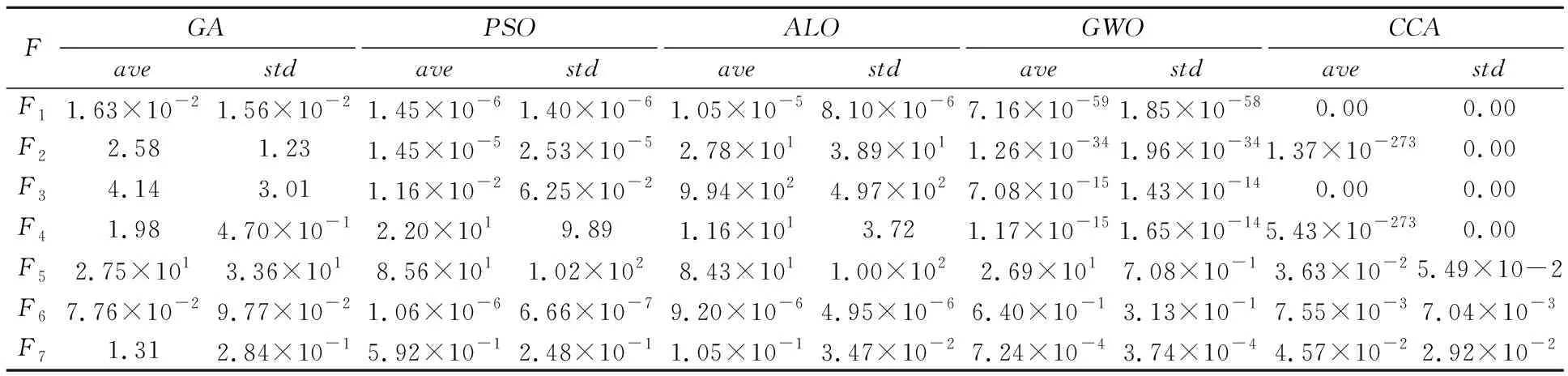
表2 单峰基准函数优化结果比较(30维)

图5中展示了收敛曲线,由图5可知:碳循环优化算法在单峰基准函数上比其他算法具有更高的收敛速度.在迭代的初始阶段,碳循环优化算法能够更快速地向最优值区域进行收敛.该算法在计算上是可用于解决优化问题的.

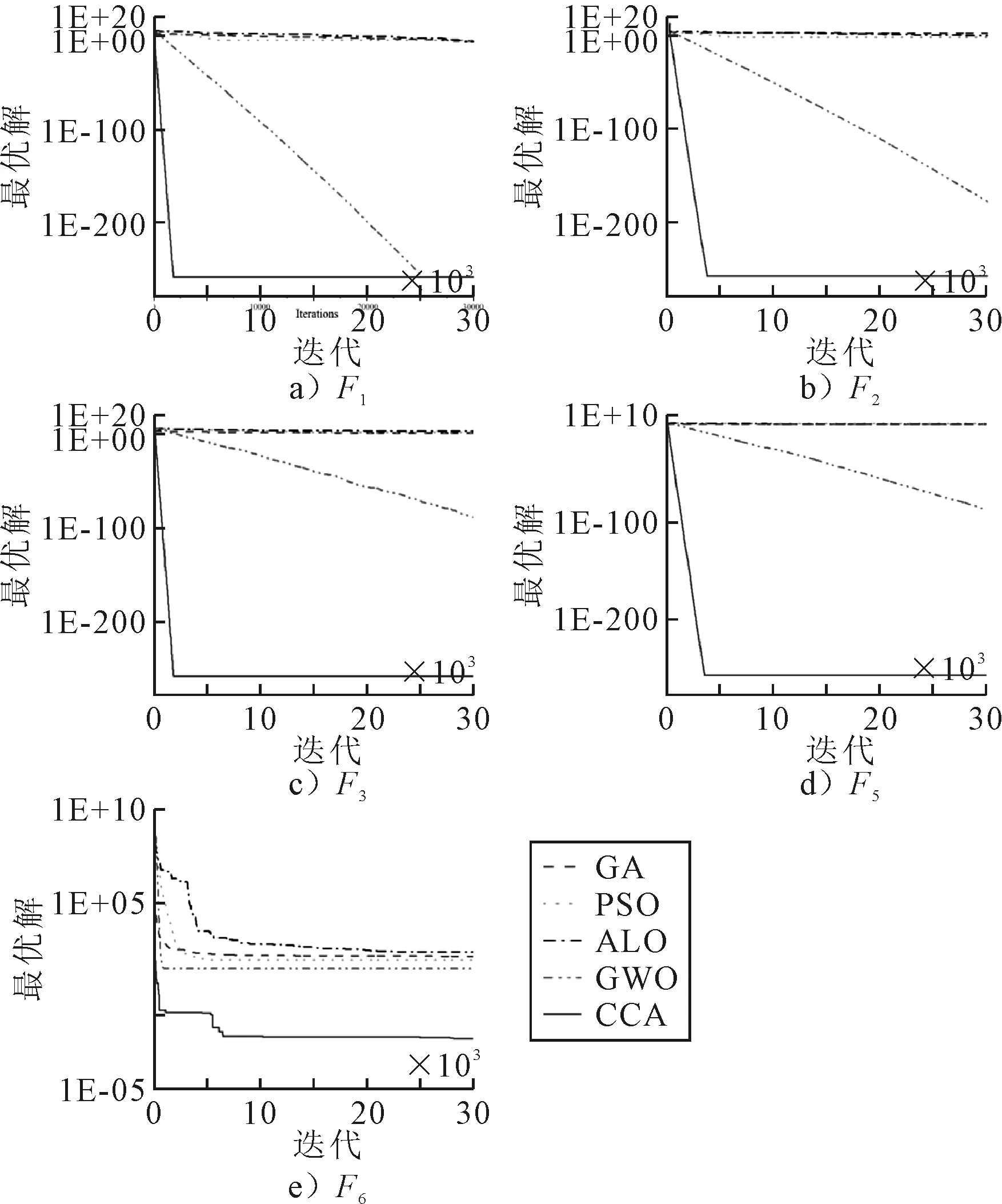
图5 对一些单峰基准测试函数CCA和其他算法的收敛性分析

2.2.2测试实验二

在实验2中,考虑了六个维度为30的多峰测试函数,并与实验1中使用的四种算法(PSO、GSA、GWO和ALO)进行了比较.这些函数的函数图像对应于图6,具体的函数表达式对应表3.总体种群规模和最大迭代次数与实验1中的相同.表4为30次独立运行的平均实验结果,图7为基准函数F9、F10和F11的收敛曲线.

图7 对一些多峰基准测试函数CCA和其他算法的收敛性分析

表3 多峰基础测试函数

由图6可知:多峰函数有许多局部最优解,这些局部最优解的数量随着函数维数的增加呈指数增长.由表4可知:除了F8函数外,CCA算法的性能优于所有算法.该算法可以避免局部最优,并在多模态基准函数上提供许多有竞争力的结果.

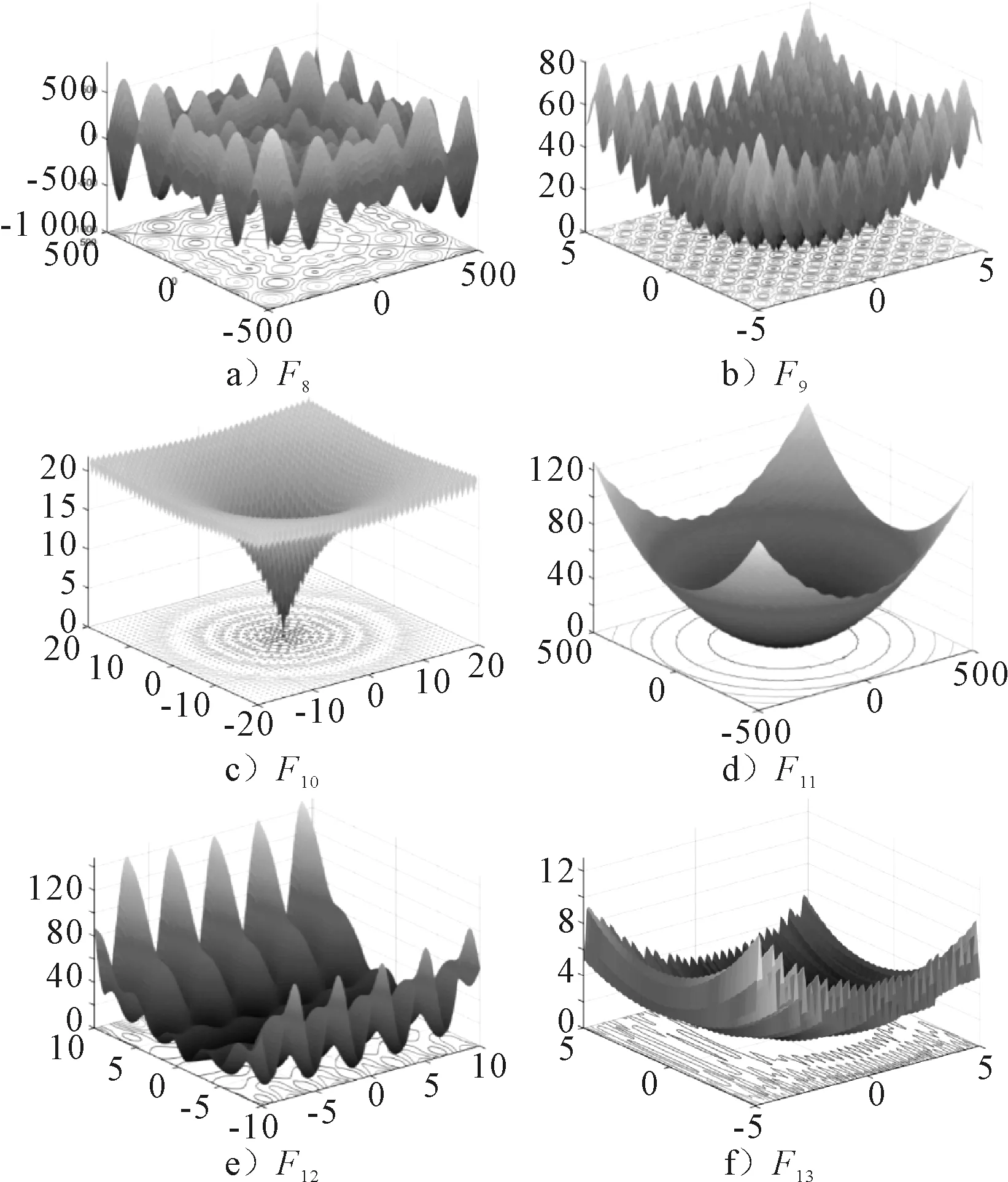
图6 多峰测试函数对应的函数图像

由上可知:CCA算法的效果比较显著.从收敛曲线的角度来看,CCA总是在测试函数中快速向最优解移动.这可以与算法进行比较.

3 船舶航行路径规划流程

碳循环优化算法的船舶航行路径规划流程图见图8.

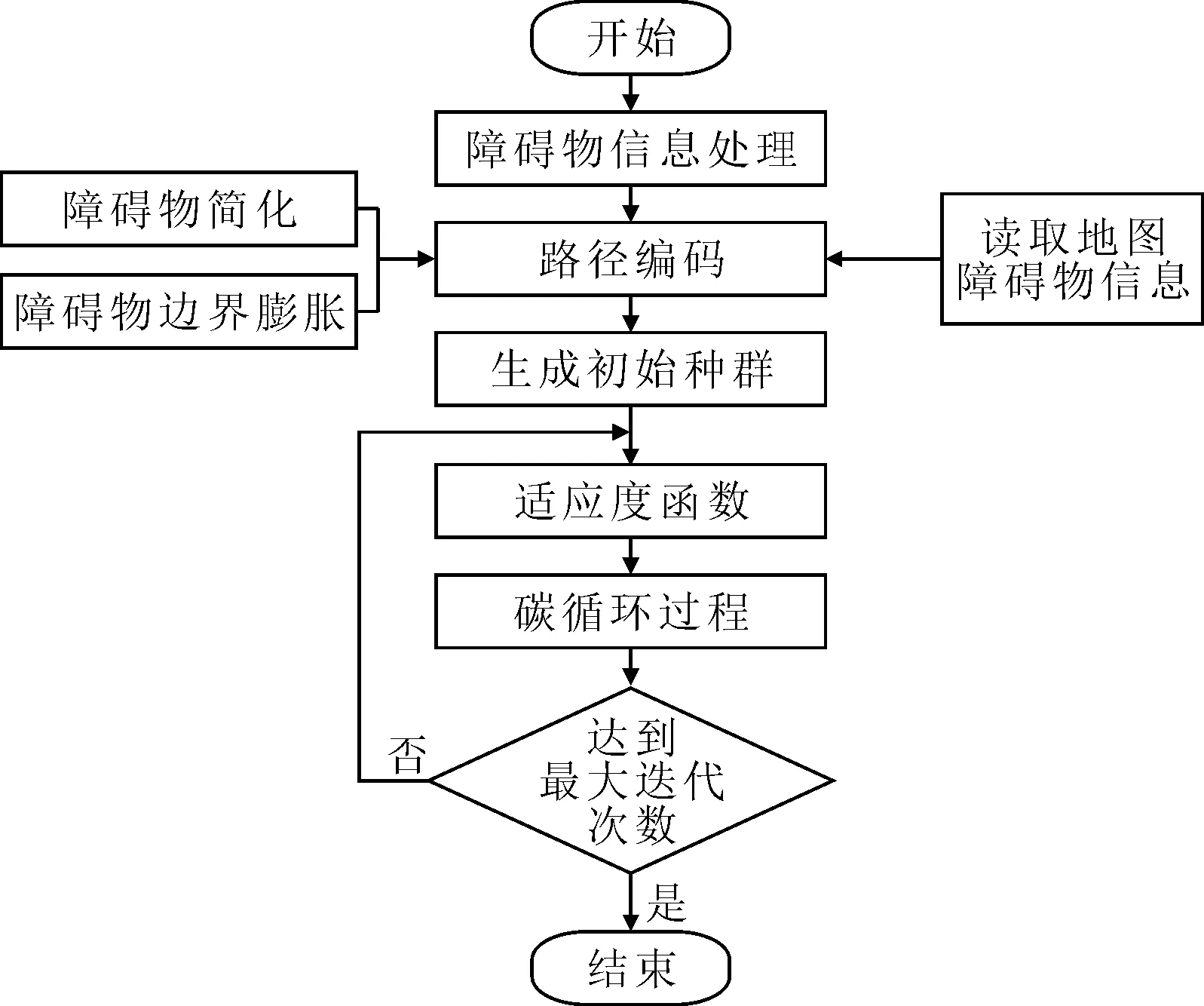
图8 技术路线图

4 仿真验证及分析

选取舟山附近水域岛屿较多的复杂水域环境构建环境模型,所选水域见图9.

图9 舟山水域地图

通过提取海图数据得到障碍物边界信息,将多边形边界根据船长进行膨胀处理.经过简化及膨胀处理后该水域的环境模型见图10.

图10 几何图法生成障碍物模型

基于构建好的环境模型,分别选取遗传算法(GA),基于膜系统的扩散算法(DAPS),鲸群优化算法(WOA)与文中的碳循环优化算法(CCA)在相同的仿真环境下进行结果对比,DAPS为武汉理工大学高性能船舶技术教育部重点实验室汪皓开发的一种群智能优化算法[6-7].四种算法种群数量设为50,最大迭代次数设为200.规划得到的路径见图11.该结果为在不同算法中运行30次的平均结果.表5 为应用四种算法所生成的规划航行路径在安全性,航行距离及适航性的数据.

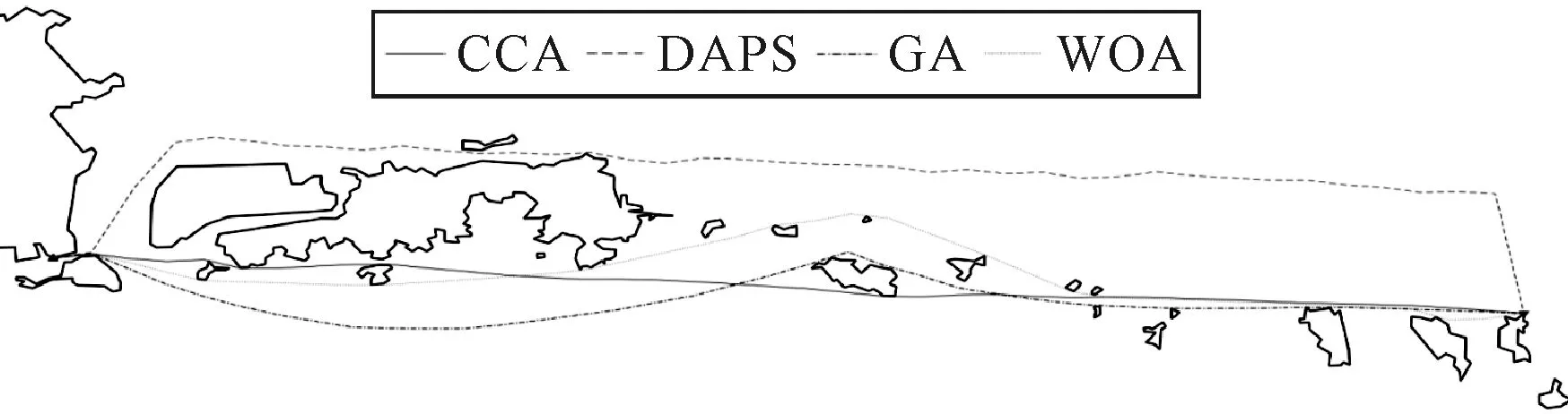
图11 四种算法生成的规划路径

表5 算法结果对比

在环境建模时,对障碍物进行了膨胀,因此四种算法生成的航行路径均与障碍物有一定的安全距离都能满足安全航行的需求[8-9].根据地图测距,起点至终点的直线距离为47 km,碳循环优化算法生成的航行路径总距离为47.5 km,相比其它算法优化效果提高2.1%以上,同时所生成的路径无较大转角船舶沿规划航线航行时更容易操纵.通过上述分析表明,本文基于碳循环优化算法可以正确的、满足多种要求的自动生成船舶航行路径且求解得到的路径更优.

5 结 束 语

本文提出一种基于碳循环优化算法的船舶智能航行路径规划方法,说明了方法的基本思想、设计内容以及实现过程,并且通过仿真实验证明该方法可以满足多个准则下自动生成满足约束的船舶航行路径,而且得到的规划方案效果较传统规划方法.另外,本文研究尚有不足,如没有考虑更多航行影响因素(如风、浪、流、能见度等)达到更符合真实航行环境的航行路径规划效果,后续有待进一步研究.