高速公路避险车道平面参数可靠性设计

张 航 刘 洋

(武汉理工大学交通与物流工程学院 武汉 430063)

0 引 言

山区高速公路连续长大下坡路段是影响高速公路总体安全水平的主要隐患,也是一直以来交通安全保障研究的重点.根据多年实践证明,避险车道对降低山区高速公路交通事故的频率和严重程度有较好的效果.

刘攀等[1]基于集料颗粒流模型进行仿真模拟,结合实际试验结果,确定了避险车道铺设厚度、长度等设计技术参数.徐建国等[2]提出新型气囊式避险车道,运用有限元分析软件ABAQUS/Explicit进行模拟,证明了其可行性.宋灿灿等[3]对避险车道驶出角度及引道长度、全宽型服务车道设置位置、辅助车道、左转和右转圆曲线处流出角度进行了研究,通过驾驶模拟分析了避险车道的各个指标,得出了各参数的建议范围.孟志豪[4]通过分析避险车道的设计理念及过程,给出了避险车道的具体位置、技术要点和其余设施的设计方法.以上研究在避险车道设计以规范值等确定性设计方法为主,相应的参数、指标变化对预期安全效果的影响不够明确,这种确定性的分析方法在某些情况下不能为驾驶人提供足够的行车安全保障,因此引入结构工程可靠度理论,考虑变量的随机性和不确定性,将原有设计方法中的“确定性”转变为“不确定性”,通过可靠度或失效概率来直观地衡量道路安全性,更加符合实际情况.

可靠度理论在道路工程领域应用广泛.Navin[5]将可靠度引入公路设计领域,用于指导路线几何设计.张航等[6]运用可靠度理论对高速公路平曲线超高进行设计.唐宗鑫等[7]利用可靠度方法计算加速车道长度.王路等[8]基于可靠度计算高速公路临界坡长.可靠性设计思想能考虑现实世界的离散性、不确定性,设计结果更为合理．因此,在道路设计领域,可靠性设计思想和方法正在逐步推广应用.文中将避险车道的主要平面设计参数的相关影响因素研究与可靠度理论结合,进行可靠性分析,将其平面设计参数指标安全程度量化,有利于推广可靠度在道路工程领域的应用,提高道路安全性.

1 避险车道

避险车道一般设置于连续长陡下坡的坡中段或坡底段,主要由引道、制动坡床、救援服务车道、相关的交通标志标线、护栏等交通安全设施和照明与监控报警系统等其他附属设施组成,其结构组成见图1.

2 平面设计参数可靠性分析

2.1 可靠度基本概念

可靠度是指工程结构在规定的时间和条件下,完成预期指标、取得预期结果的概率.此概率即为可靠概率Ps,而与之对应的为失效概率Pf,Ps+Pf=1,即将可靠度理论引入到避险车道设计中,使得车辆能安全驶入避险车道并安全减速停车的概率为Ps,反之为Pf,将避险车道驶入角超过安全值和引道长度小于安全值与失效状态相对应,并计算出失效概率以表示设计值中超出安全范围部分可能存在的安全隐患.

2.2 构造可靠度功能函数

1) 驶入角可靠度功能函数 制动失效车辆能安全驶入避险车道的驶入角,记为αR;设计避险车道所提供的驶入角,记为αS.当αR>αS,可认为设计值处于失效状态,此时设计存在安全隐患.因此,可靠性功能函数可设为

Z=g(αR,αS)=αR-αS

(1)

2) 引道长度可靠度功能函数 制动失效车辆进入避险车道后,驾驶员有足够时间进行调整的引道长度,记为LR;设计避险车道所提供的引道长度,记为LS.当设计引道长度小于安全引道长度时,可认为设计值处于失效状态,此时设计存在安全隐患.因此,可靠性功能函数可设为

Z=g(LR,LS)=LS-LR

(2)

2.3 构造计算模型

2.3.1驶入角计算模型

车辆从离开主线行驶至进入避险车道引道的过程中,车辆转过的角度为驶入角,设计中常取为分流处主线最右侧车道(切线)与避险车道引道之间的夹角.避险车道分为左转平曲线、右转平曲线和直线三种,本文选取主线为右转平曲线类作为研究对象,见图2.

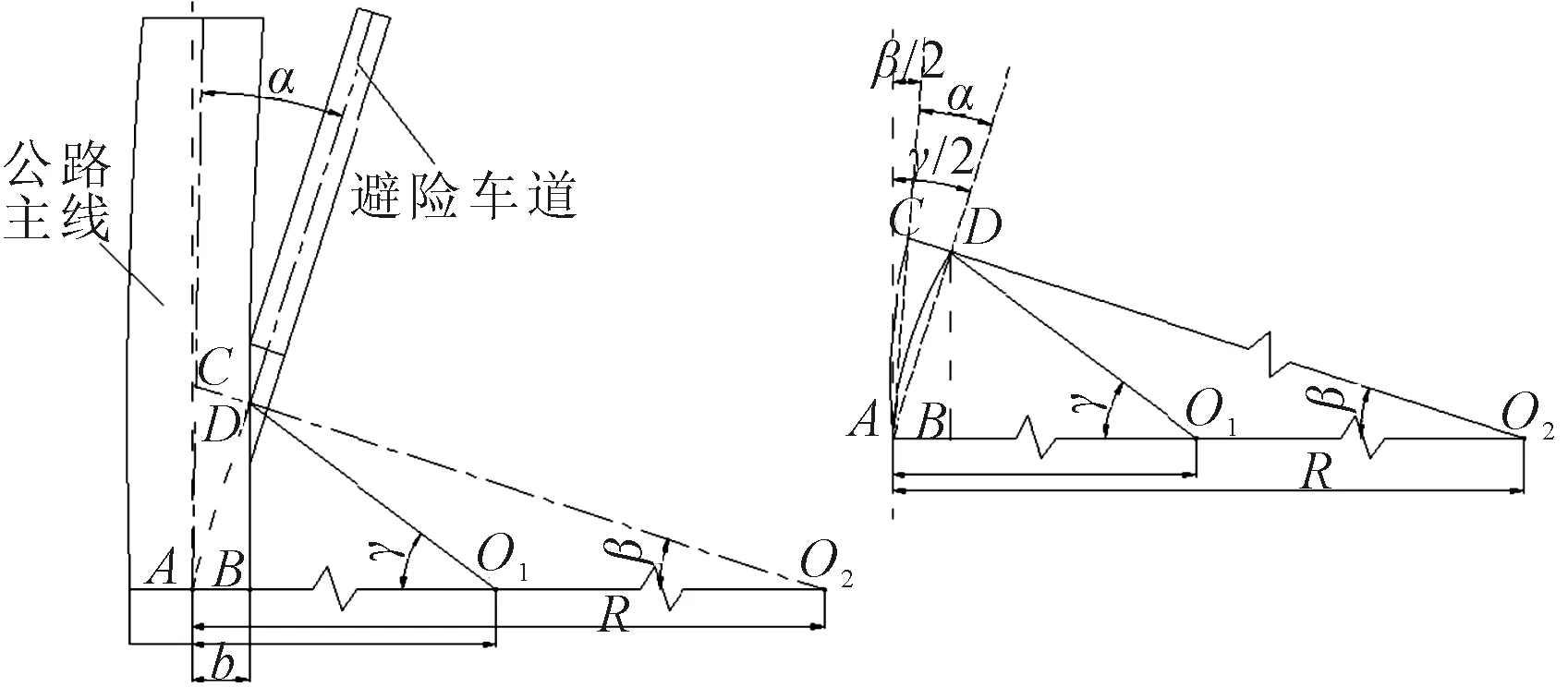
图2 主线为右转曲线时避险车道驶入角计算示意图

(3)

当汽车在曲线上行驶时受到离心力的作用,需避免发生横向滑移或横向倾覆,一般有先发生横向滑移后发生倾覆,防止横向滑移则有

(4)

因此,将不发生横向滑移的极限半径R作为车辆转向行车轨迹半径r代入式(3)可得:

(5)

式中:αmax为避险车道驶入角最大安全值,(°);v入为失控车辆在避险车道入口的驶入速度,km/h;φh为横向附着系数,一般φh=(0.6～0.7)φ,取最不利状态下即路面为潮湿的沥青混凝土路面,此时φ为0.4,φh为0.24;ih为路拱横坡(一般取2%).

2.3.2引道长度计算模型

避险车道引道连接着公路主线与制动坡床,其作用是保障制动失效车辆能顺利驶出主线进入避险车道,是十分重要的衔接过渡段.引道长度为

(6)

式中:Lmin为避险车道引道最小安全长度,m ;t1为驾驶员反应时间,s;t2为车辆对驾驶员操作响应时间,s;v入为失控车辆在避险车道入口的驶入速度,km/h.对于现代车辆,t1远大于t2,因此t1+t2近似取为t1.

2.4 影响变量分析

2.4.1车辆驶入避险车道速度v入

阎莹等[9]对多个选定断面得到的车速数据进行随机抽样,并结合P-P概率分布图和单样本K-S检验法进行多种常见分布的检验,得出高速公路断面运行速度总体分布服从正态分布,同时可以得出制动失效车辆驶入避险车道速度v入也近似服从正态分布.据此选取多个不同地区和不同主线设计速度(120,100,80 km/h)的位于直线或大半径平曲线路段的高速公路避险车道进行调查,对所选避险车道入口处的大型车驶入车速进行测量,利用统计分析软件SPSS进行单样本K-S检验,结果见表1.

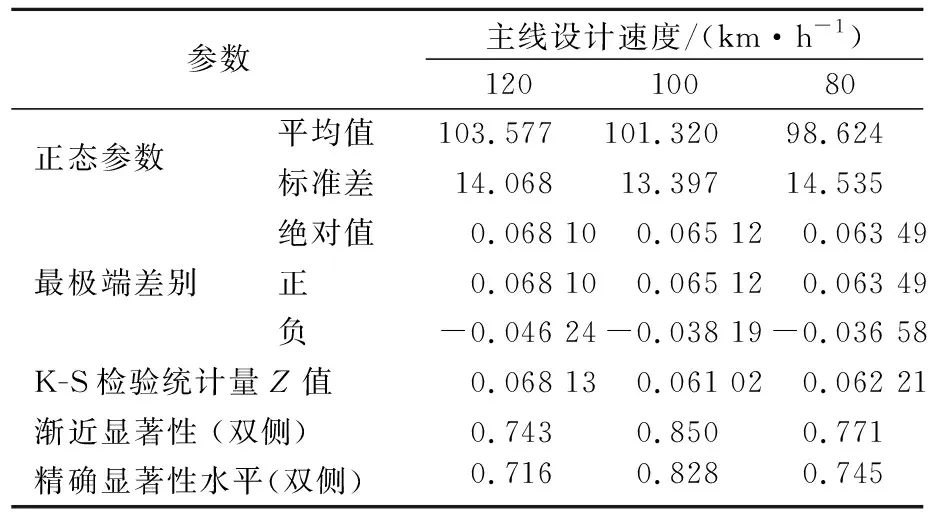
表1 高速公路避险车道大型车驶入车速速度K-S检验结果

从K-S检验结果可以看出,主线设计速度为120,100,80 km/h所对应的统计值精确显著性水平分别为0.716、0.828、0.745,均大于95%的置信度水平代表值0.05,则所观测样本的总体即大型车避险车道驶入车速的分布服从正态分布.

2.4.2主线车辆行驶半径R

林雨等[10]对车辆在双车道公路弯道的行车轨迹半径进行研究,通过实地测量试验得出各观测断面处的行车轨迹侧向偏移量,得出行车轨迹侧向偏移量近似呈正态分布,则可近似认为车辆实际转弯半径也服从正态分布.研究中行车轨迹侧向偏移量的正态分布参数与半径设计值的关系,计算出不同主线设计速度下的极限最小半径所对应的实际转弯半径的正态分布参数,结果见表2.

表2 车辆实际转弯半径正态分布参数

2.4.3驾驶员反应时间t1

驾驶员的反应时间近似服从正态分布或对数正态分布,总结见表3.

表3 不同因素的反应时间分布参数比较

取最不利情况下的反应时间,其服从正态分布,其均值为1.51 s,标准差为0.39 s.

3 可靠度功能函数求解

3.1 驶入角

文献[11]规定避险车道与主线的夹角宜小于5°,则设计驶入角αS取为5°,根据驶入角可靠度功能函数式(1)及已建立的驶入角计算模型,采用表1～2的变量分布参数值v入和R,通过验算点法进行迭代计算,取允许误差ε=10-3,得出的可靠概率Ps与失效概率Pf结果见表4.

由表4可知:经过多次迭代计算直至验算点之差小于允许误差ε=10-3后,所得相应的可靠度概率和失效概率等值已满足精度需求,依此可进行可靠度分析.

表4 驶入角可靠度计算结果

3.2 引道长度

文献[11]规定避险车道引道长度不宜小于70 m,则设计引道长度LS取为70 m,根据引道可靠度功能函数式(2),采用表1和表3中的变量v入和t1分布参数值,通过蒙特卡罗法进行求解.具体步骤如下.

步骤1确定抽样模拟过程所得样本容量,即抽样次数取为N=10 000.

步骤2利用Matlab等计算机软件对失控车辆驶入避险车道速度v入、反应时间t1抽样模拟.其中,v入的值来源于根据表1中对应的均值和标准差进行正态分布抽样模拟产生的随机数;t1的值来源于根据表3中对应的均值和标准差进行正态分布抽样模拟产生的随机数,其服从正态分布,其均值为1.51 s,标准差为0.39 s.

步骤3抽样模拟得出v入、t1的值后,将其带入功能函数式(2)算.

步骤4若某次抽样模拟后功能函数式中Z≥0,则定义此次抽样为一次可靠抽样,同理定义Z<0时为一次失效抽样.

步骤5重复上述步骤2～4,直至抽样次数大于10 000次.

步骤6统计所有的可靠抽样与失效抽样次数,其与总体样本容量的比值即为蒙特卡罗法得出的可靠概率与失效概率.

可靠概率Ps与失效概率Pf结果见表5.

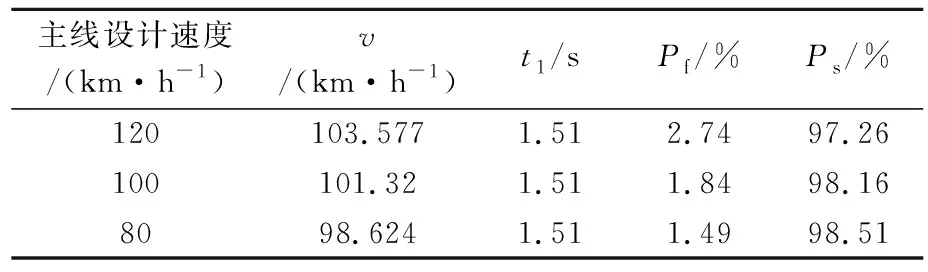
表5 引道长度可靠度计算结果

4 计算结果分析

现行的道路设计标准与规范中,未对避险车道各设计参数的可靠度作出明确规定.当设计取值处于失效状态时,可认为与结构的失效状态相近,参考文献[12]中对高速公路路面结构目标可靠度的规定来确定高速公路避险车道的可靠概率和失效概率,不同安全等级对应的可靠概率与失效概率见表6.

表6 不同安全等级对应的可靠概率与失效概率

由上节中对主线设计速度为120,100,80 km/h的避险车道驶入角可靠度计算结果,当αS=5°时,可靠概率分别为41.67%、42.92%和42.37%,均小于95%,不满足要求.造成不满足要求的原因可能为:一是避险车道驶入角计算模型式(1)更符合制动失效车辆驶入避险车道时的实际情况,比规范固定值5°更安全.二是考虑了随机变量参数的分布与不利组合情况,避险车道驶入速度v入和车辆主线行车轨迹半径R并不总为设计值,具有离散性的特点.利用可靠度功能函数计算时,考虑到了驶入角影响参数的各种不利组合,得出的可靠概率值更能反映实际情况.

当LS=70 m时,可靠概率分别为97.26%、98.16%和98.51%,均大于95%,均满足要求.分别根据避险车道驶入角和引道长度可靠度功能函数可以计算出满足目标可靠概率95%的驶入角最大安全设计值和引道长度推荐取值见表7～8.

表7 驶入角最大安全设计值与推荐选用值

表8 引道长度最小安全设计值与推荐选用值

5 工程实例

高速公路项目一全长123.7 km,主线设计速度为80 km/h.项目一中连续下坡路段长度为16.9 km,平均坡度为-2.9%,最大纵坡坡度为-4.2%,在坡中段和坡底段共设置4条避险车道,其序号分别为1、2、3、4.

高速公路项目二全长102.2 km,主线设计速度为100 km/h.项目二中连续下坡路段长度为7.3 km,平均坡度为-3.2%,最大纵坡坡度为-3.8%,在坡底段设置2条避险车道,其序号分别为5和6.

从相关部门调查结果可得两条高速公路6条避险车道发生的事故,表9细列出了6条避险车道2019—2021全年的事故次数汇总.

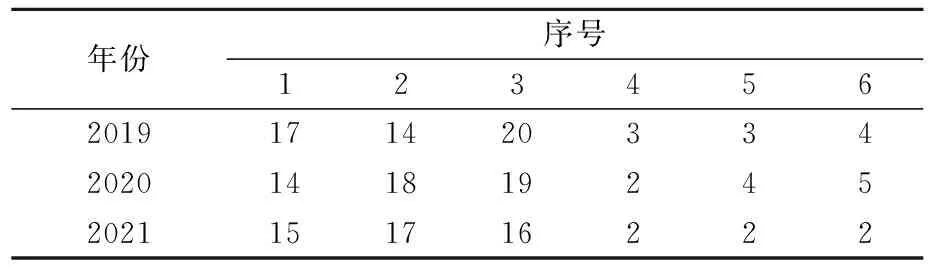
表9 2019—2021全年的事故次数汇总

由表9可知:第1、2、3条避险车道相比于其他三条避险车道发生事故次数更多,说明其设计参数方面有一定问题,其避险车道具有较大安全隐患.

根据这6条避险车道的设计资料,对其驶入角和引道长度进行统计,得出结果见表10.

表10 避险车道驶入角与引道长度统计表

根据规范设计驶入角αS=5°和设计引道长度LS=70 m可得,4、5、6条避险车道驶入角和引道长度设计值均满足规范,第1条避险车道的驶入角和引道长度的设计值均不满足规范,第2、3条避险车道只有驶入角不满足规范.

针对表10中各避险车道驶入角和引道长度数据,对每个避险车道的设计参数实际取值进行可靠性分析,利用一次二阶矩法计算得出其失效概率,计算结果见表11～12.

由表11可知:1、2、3号避险车道驶入角设计值的失效概率分别为61.5%、81.6%、61.5%,均大于5%,不满可靠性要求,具有安全隐患,与表9中的事故次数实际情况相符,应对其设计做出调整,即1、2、3号避险车道的驶入角设计值均应调整为不大于4.4°.4、5、6号避险车道驶入角设计值的失效概率分别为<0.1%、<0.1%、3.6%,均小于5%,满足可靠性要求.由表12可知:6条避险车道引道长度设计值的失效概率均小于5%,满足可靠性要求,出于节省材料经费考虑,可取对应的引道长度建议值.

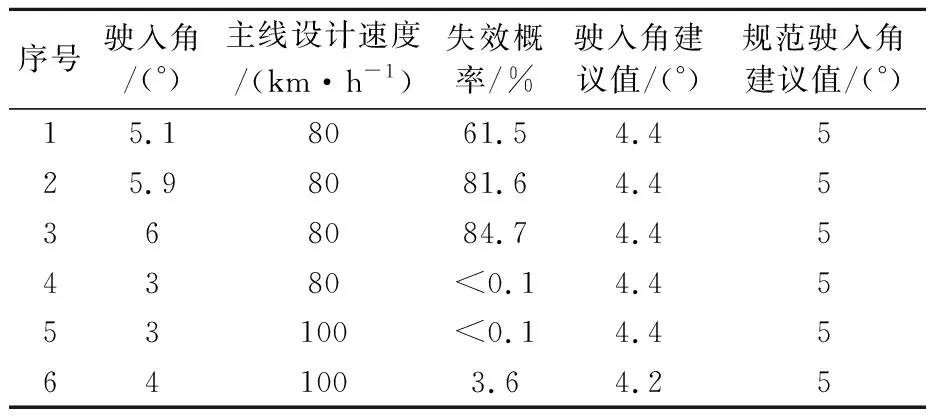
表11 车道驶入角失效概率计算结果

6 结 论

1) 结合相关研究对避险车道的设置情况和主要结构与功能进行分析,以避险车道的两个平面设计参数:驶入角和引道长度作为研究对象,根据几何约束分别确定计算模型,得出与避险车道驶入角和引道长度相应的影响因素.

2) 将结构工程可靠度理论应用于道路设计领域,根据计算模型建立了驶入角和引道长度的可靠度功能函数.分析相关的影响变量“驶入速度、车辆主线行车轨迹半径、驾驶员反应时间”的分布情况及其参数,采用验算点法和蒙特卡罗法进行可靠度求解,分析驶入角和引道长度设计值的失效概率.得到高速公路三种主线设计速度120、100、80 km/h下,驶入角可靠概率分别为41.67%、42.92%和42.37%,安全可靠程度不足;引道长度可靠概率分别为97.26%、98.16%和98.51%,满足预期安全可靠程度.

3) 采用可靠性设计方法进行避险车道平面设计,以高速公路路面结构的目标可靠度为预期安全目标,计算得到三种主线设计速度120、100、80 km/h时具有95%可靠概率的驶入角和引道长度建议取值,计算结果为:主线设计速度为120 km/h的高速公路最大安全驶入角建议值为4°,最小安全引道长度建议值为65 m;主线设计速度为100 km/h的高速公路最大安全驶入角建议值为4.2°,最小安全引道长度建议值为64 m;主线设计速度为120 km/h的高速公路最大安全驶入角建议值为4.4°,最小安全引道长度建议值为63 m.