基于时空图卷积网络的城市交通流预测模型
2023-05-12路佳玲魏志成
路佳玲 魏志成 田 多
(河北师范大学计算机与网络空间安全学院1) 石家庄 050024) (河北师范大学河北省网络与信息安全重点实验室2) 石家庄 050024)
0 引 言
近年来,国内智能交通系统(intelligent transportation system, ITS)发展迅速,交通预测作为ITS的重要内容,正在受到学者们的广泛关注.准确的交通流量预测可以提高城市居民出行效率,加强城市交通管理水平.
交通流量的预测方法主要分为模型驱动和数据驱动两大类.模型驱动方法由于模型固定,预测结果通常会不尽人意,因此人们已将预测的重点转变为数据驱动方法[1-2].数据驱动方法包括统计分析模型和机器学习模型两大类.历史平均模型(historical average, HA)和自回归综合移动平均模型[3](autoregressive integrated moving average, ARIMA)是统计分析模型的经典方法,算法简单,易于实现.然而这种模型会受到时间序列平稳性假设的限制,因此无法有效的预测具有高度非线性和复杂性特征的交通数据.常用的机器学习方法包括K近邻、随机森林、支持向量回归(support vector regression, SVR)等,与统计分析模型相比,机器学习模型通常可以达到较好的预测效果.
机器学习模型通常架构浅易,在处理大规模、高复杂度的数据时,会显得稍有不足.面对高度非线性和复杂性的交通数据,深度学习方法展现出巨大的优势.Ma等[4]采用长短期记忆网络(long short-term memory, LSTM)进行交通速度预测.Zhang等[5]结合天气条件数据,采用门控循环单元(gate recurrent unit, GRU)预测城市交通流.Vijayalakshmi等[6]基于注意力机制,使用卷积神经网络(convolutional neural network, CNN)和LSTM进行交通流预测.
交通数据包含了空间信息,具有非欧几里得的拓扑结构[7].然而传统的深度学习方法无法很好的处理非欧几里得数据.近年来,图卷积神经网络[8-9](graph convolutional network, GCN)越来越多的被用于交通预测任务中.GCN将一组节点及节点间关系构成的图作为输入,从而提取出节点间的空间关联性.Yu等[10]提出了时空图卷积网络(spatio-temporal graph convolutional network, STGCN)预测交通速度.Guo等[11]使用注意力机制并结合GCN和标准二维卷积预测交通流.Zhao等[12]结合GCN和GRU进行交通预测.
现有的基于GCN的交通流预测模型通常将研究重点放在网络层的结构上,而忽略了邻接矩阵的构建.在图卷积网络中,邻接矩阵的质量对网络性能的好坏有很大的影响.文中提出一种预测城市交通流的多因子图构建时空图卷积网络(multi-factor graph construction spatio-temporal graph convolutional network, MFGC-STGCN),从节点间交互交通流数量、交互时间代价、流出交通流相似度三个角度出发,构造更精确的邻接矩阵.并用实例验证了模型的预测性能.
1 交通流预测问题定义
将交通网络定义为无向图G=(V,E,A),其中V为节点集;E为边集;A∈RN×N为图G的加权邻接矩阵.文中将研究区域栅格化为N个地块,对应于V中的N个节点.每个节点记录了地块的交通流量.
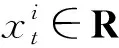
2 MFGC-STGCN交通流预测模型
2.1 模型框架
针对城市的复杂交通流,文中提出了MFGC-STGCN模型进行交通流预测任务.此模型从时间和空间两个维度提取交通流的时空特征,从而提高预测精度.MFGC-STGCN模型结构见图1.模型由两个模块组成,一个是构建加权邻接矩阵的模块,一个是图卷积网络模块.利用交通数据计算节点之间的关联,得到图的加权邻接矩阵A,并将其作为空间卷积层的输入.空间卷积层基于GCN提取空间特征,时间卷积层基于门控线性单元(gated linear units, GLU)提取时间特征.其间还通过一维卷积层再次提取时间特征,在时间轴上进行降维.
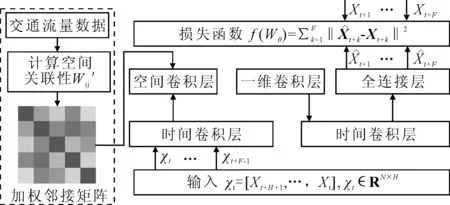
图1 MFGC-STGCN结构框架
(1)
2.2 交通数据图表示
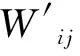
w2×Pearson(Oi,Oj)
(2)
(3)
设w1=w2=0.5.

(4)
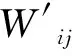
2.3 时间卷积层
时间卷积层使用GLU提取城市交通流的时间动态特征.模型共有两个时间卷积层,以第一个为例,结构见图2.Xl∈RN×H×Cin为第一个时间卷积层的输入;Cin为输入通道数,第一个时间卷积层的Cin=1.Xl+1∈RN×(H-Kt1+1)×Cout为第一个时间卷积层的输出,也是空间卷积层的输入;Cout为输出通道数.对Xl进行一维卷积,卷积核Γ∈RKt1×Cin×2Cout,得到输出Xl′∈RN×(H-Kt1+1)×2Cout.将Xl′分为相同大小的两部分,一部分使用残差连接,另一部分使用sigmoid函数进行激活.然后计算两部分输出的Hadamard乘积,从而得到第一个时间卷积层最终的输出Xl+1.
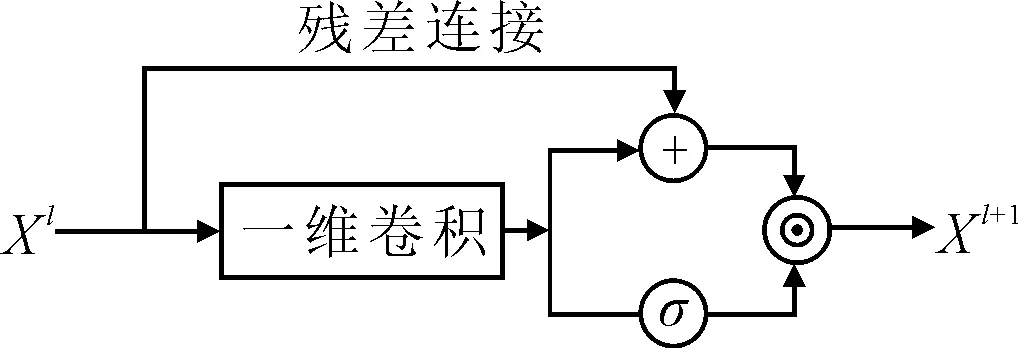
图2 时间卷积层结构
第二个时间卷积层的输入为Xl+3∈RN×(H-Kt1-Kc+2)×Cin,输出为Xl+4∈RN×(H-Kt1-Kc-Kt2+3)×Cout.Kc为一维卷积层的卷积核宽度,Kt2为第二个时间卷积层的卷积核宽度,H-Kt1-Kc-Kt2+3=1.
2.4 空间卷积层
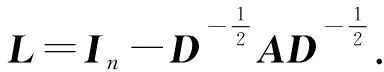
gθ*Gx=UgθUTx
(5)
式中:卷积核gθ=diag(θ),参数θ∈RN;*G为图卷积操作;UTx为信号x的图傅里叶变换.
当图规模较大时,对L进行特征分解的计算量大,因此引入切比雪夫多项式.
(6)

空间卷积层在第一个时间卷积层之后,首先将第一个时间卷积层的输出Xl+1和邻接矩阵A输入至空间卷积层.空间卷积层的输入为Xl+1∈RN×(H-Kt1+1)×Cin,其中Cin为空间卷积层的输入通道数,也等于第一个时间卷积层的输出通道数.空间卷积层同样采用了残差连接.将输入Xl+1经过切比雪夫图卷积得到的结果与输入Xl+1相加,然后经过ReLU激活函数,得到输出Xl+2∈RN×(H-Kt1+1)×Cout.
2.5 一维卷积层
一维卷积层在空间卷积层之后.它再次提取时间特征,对数据在时间轴上进行降维.一维卷积层的输入经过卷积核宽度为Kc的卷积操作,时间步由H-Kt1+1变为H-Kt1-Kc+2.最后使用Dropout正则化防止过拟合.Dropout正则化是深度学习领域最受欢迎的正则化技术,它会在迭代过程中以一定的概率随机选择神经元使其失活,从而降低神经元之间的依赖性.
3 实验与评估
3.1 数据准备
使用2018年3月石家庄二环范围的网约车OD数据作为数据集.在对原始数据进行预处理后,每一条记录包括上车位置和下车位置(经度和纬度)、上车时间和下车时间6个字段.将研究区域栅格化为340个地块,以15 min为时间间隔,地块流量定义为地块内上车量与下车量之和.选取历史数据的前70%作为训练集,其余为验证集和测试集.此外,对实验数据进行了z-score归一化.
3.2 参数设置
MFGC-STGCN模型除第一层的输入通道数和最后一层的输出通道数为1,其余通道数均设置为64.σ设置为0.3,H设置为12,K、Kt1、Kc均设置为3,Kt2设置为8.模型训练的批次大小为32,优化器为AdamW.学习率初始值为0.001,并随着训练过程不断衰减.
3.3 评价指标
使用平均绝对误差(mean absolute error, MAE)和均方根误差(root mean square error, RMSE)评价模型性能.两个指标为
(7)
(8)
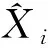
3.4 实验结果与分析
将文中的模型MFGC-STGCN与HA、FNN、LSTM、GRU、STGCN等模型进行对比,见表1.由表1可知:MFGC-STGCN在所有模型中表现出最佳的预测效果.传统的统计分析模型HA由于无法分析复杂的交通数据,预测效果最差.基于深度学习方法的模型预测结果均优于HA.结合了GCN的STGCN和MFGC-STGCN优于深度学习模型.其中MFGC-STGCN的MAE较STGCN降低了0.223,RMSE降低了0.309.
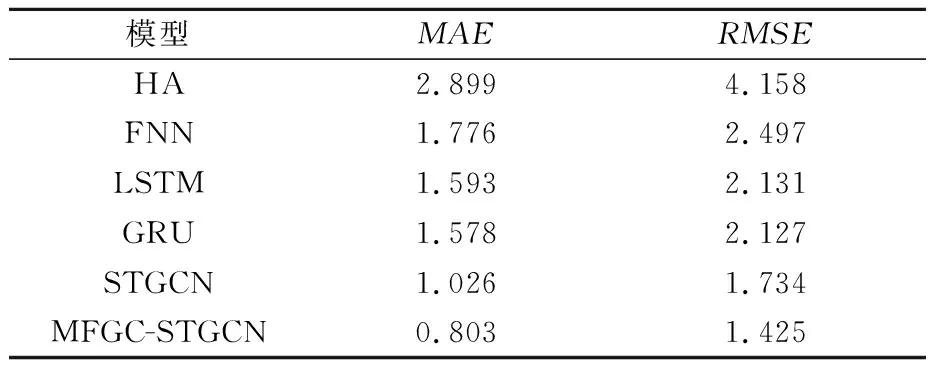
表1 不同模型预测性能对比
选取五个流量较大的地块,对它们不同时间段平均流量的预测结果进行可视化,见图3.由图3可知:MFGC-STGCN和STGCN模型的拟合程度较好.其中,文中算法MFGC-STGCN的拟合效果最好,预测值和真实值误差最小.LSTM、GRU、FNN的拟合效果相对较差.特别是FNN,在流量较低的时间段,预测值普遍比真实值偏高,在流量较高的时间段,预测值普遍比真实值偏低.
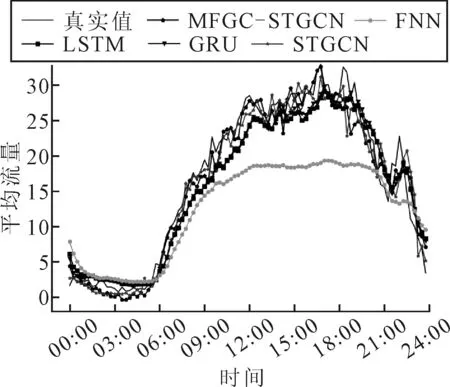
图3 不同模型预测效果可视化
图4为MFGC-STGCN和STGCN模型的预测误差.预测误差指在对应时间点所有地块预测值与真实值的绝对误差之和,文中对纵轴进行了归一化.由图4可知:在绝大部分时间点中,MFGC-STGCN的误差明显小于STGCN.图5为随着训练轮次增加,测试集MAE的变化曲线.MFGC-STGCN和STGCN的MAE初始值接近,但相比之下MFGC-STGCN的收敛速度更快.在40~100轮次,MFGC-STGCN的MAE下降迅速.所有试验在Windows操作系统(Intel(R) Core(TM) i5-6500 CPU @ 3.20 GHz)上运行.与STGCN相比MFGC-STGCN训练速度更快,MFGC-STGCN训练1个epoch大约需要51 s,STGCN训练1个epoch大约需要95 s.

图4 不同模型的预测误差可视化
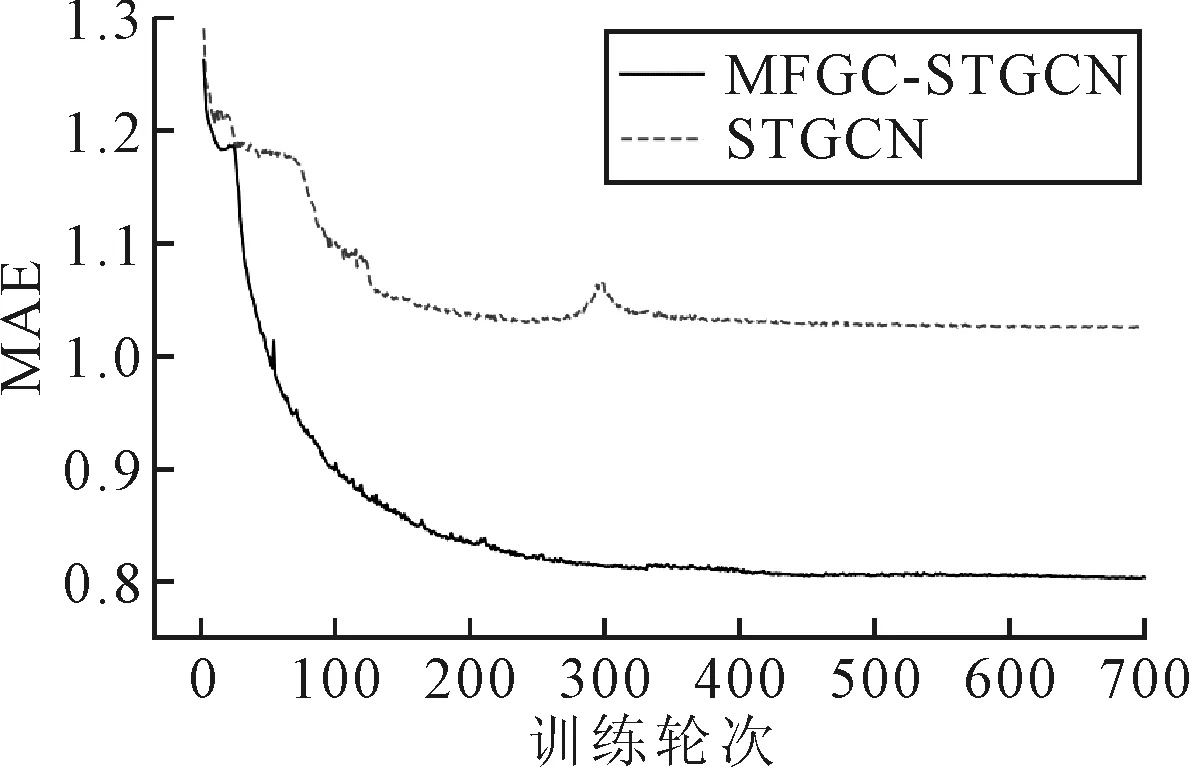
图5 测试集MAE随训练轮次的变化
4 结 束 语
文中提出的MFGC-STGCN模型可以有效的挖掘交通数据的时空信息,MFGC-STGCN模型从时间和空间两个维度提取交通流的特征,预测效果明显优于仅提取时间特征的经典模型.同时,MFGC-STGCN模型与同样提取交通流时空特征的STGCN模型相比,使用的参数数量更少,训练速度更快,预测准确率更高.但在现实生活中,天气情况、社会事件等外部因素对交通流量具有一定的影响.后续研究将MFGC-STGCN模型融合一些外部因素,进一步提高预测精度.
