基于某型飞行器卫星定位航迹修正算法的研究
2023-05-12梁明何超
梁明,王 刚,何超
(中国人民解放军91851 部队,辽宁 葫芦岛 125001)
0 引言
某型飞行器作为一种一次性使用的航天产品,属于消耗型产品,在保证飞行精度的同时如何有效降低成本是值得探索的问题。卫星导航技术作为一种成熟的应用技术,在无人飞行器控制中应用越来越广泛[1],本文以北斗为例,对如何采用卫星定位信息有效提高飞行器侧向弹道散布精度的算法进行研究,并设计出控制规律,经验证达到试验指标要求。
1 飞行器航向控制通道分析
飞行器航向通道采用稳定航向角的比例-积分-微分(Proportion-Integration-Differentiation,PID)控制回路[2]。这种控制方式易受射向误差、侧风、陀螺漂移等因素的干扰使飞行器偏离预定弹道,飞行器的侧向偏差有较大的随机性,且随着时间的增加,飞行器的侧偏变大。特别是舰载机动发射时,受舰船就位点误差、平台罗经误差、发射架标校误差、指挥仪装订误差等因素的影响其侧向偏差会更大[3]。
某型飞行器弹道在末端与理论弹道相差约1.0 km,飞行器射向误差与控制误差联合作用所导致的飞行器弹道侧偏过大,如图1 所示。

图1 某型飞行器弹道侧偏Fig.1 Ballistic lateral deflection of a certain type of aircraft
为减小飞行器弹道侧偏,将飞行器飞行过程中的位置信息闭环到航向控制通路中,形成对飞行器侧向位置的闭环控制。该方法可以有效减小飞行器弹道侧向误差[4]。飞行器的位置信息可以由卫星定位、惯导来提供。卫星定位价格便宜、定位精度高,但卫星定位数据更新率低,存在定位不稳定的情况;惯性导航装置价格昂贵,长时间工作时定位精度会下降,需要卫星定位对其测量信息进行修正,但惯导工作状态稳定,数据更新率高[5]。采用惯性导航时,飞行器航向通道的控制规律如图2 所示。在原飞行器航向通道控制规律的基础上,去掉航向角积分环节,增加飞行器侧向位置的PID 控制环节。侧向位置与理论弹道之差为ΔZ,ΔZ的比例、积分、微分环节的传动比分别为0.2、0.01、0.9,积分环节的限幅值为±3,微分环节的限幅值为±60,是一阶惯性环节。ΔZ经过PID 运算后进行±60 的限幅,然后与航向角的比例和微分信号求和输出给航向舵机。在航向通道增加侧向位置的闭环控制后,飞行器具备弹道的侧向位置控制功能[6]。
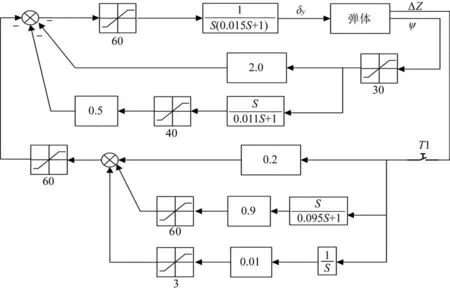
图2 惯性导航时航向通道传递函数框Fig.2 Block diagram of the heading channel transfer function for inertial navigation
2 飞行器惯导状态时仿真
为验证重新设计后航向通道的控制效果,利用飞行器仿真程序对该控制规律进行仿真[7]。惯性导航控制规律的单位阶跃响应如图3 所示。由图3 可知,该控制系统存在一个周期的超调,上升时间为11.3 s,调节时间为42.1 s,超调量为31%,稳态误差为零,惯性导航控制规律具有良好的动态性能和稳态性能。阶跃响应的超调量较大,是因为在阶跃幅值仅为1 m,在此时传递函数中的限幅环节没有起作用。在实际的控制过程中,当侧偏较大,传递函数中的限幅环节将会因达到最大值而限幅,超调量也会相应减小[8]。

图3 单位阶跃响应Fig.3 Unit step response
分别对飞行器飞行出现侧偏的典型情况进行仿真,如图4 所示。飞行器侧偏500 m 时,采用惯性导航控制的控制效果图如图4(a)~图4(d)所示,飞行器飞行5 s 后启动导航控制程序[9]。从图4(a)中可见,飞行器经一次超调后达到稳定,超调量为28.4 m。图4(b)是比例、积分、微分环节及其求和后的导航角控制信号曲线,可见导航角和积分环节以经达到限幅值。图4(c)、图4(d)可以看出飞行器的过载和姿态角,由于传递函数中限幅环节的作用,飞行器的侧向过载和姿态均满足指标要求。

图4 侧偏500 m 时的惯性导航仿真Fig.4 Simulation of inertial navigation when the lateral deviation is 500 m
飞行器射向偏差为3°时惯性导航控制效果如图5 所示。射向出现偏差时,飞行器的稳态差随着射向偏差的增大而增大。图5(a)所示飞行器的稳态误差为15 m。为保证惯性导航控制精度,飞行器的射向偏差必须在一个可控的范围内。射向偏差对该控制回路稳态误差的影响如图6 所示。

图5 射向偏3°时的惯性导航仿真Fig.5 Simulation of inertial navigation when the radial deviation is 3°

图6 射向偏差对稳态误差的影响Fig.6 Effect of shooting deviation on the steadystate error
续图5 射向偏3°时的惯性导航仿真Continued Fig.5 Simulation of inertial navigation when the radial deviation is 3°
3 飞行器卫星定位修偏状态控制规律
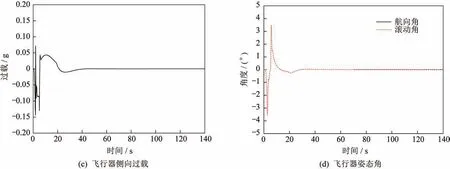
卫星定位具有良好的动态定位性能,能提供精确的位置和速度信息[10]。因此,将卫星定位接收机当成一个质心敏感元件,直接接入到航向控制回路,可构成一种简单易实施的侧向质心控制方案[11]。由于卫星定位接收机测量飞行器质心在地心直角坐标系中的位置和速度,在使用该数据时需要将卫星定位数据转换到发射坐标系下[12]。但卫星定位在使用中存在失捕和定位不稳定的现象,同时卫星定位数据更新率低,这些特性使得卫星定位的导航控制规律有所不同[13]。飞行器在发射时刻卫星定位存在失捕现象,卫星定位重新捕捉时间与卫星定位特性有关[14]。为克服卫星定位重捕时间不确定,飞行中可能存在失捕现象。而侧向开环控制根据侧向偏差输出固定的修偏程序,修偏过程中不再采样卫星定位信息,因此修偏过程中卫星是否定位对修偏程序的输出没有影响[15]。某型飞行器采用开环控制时的弹道侧偏图如图7 所示。侧偏大于500 m 时,侧偏程序启动,修偏结束后飞行器侧偏为104 m,修偏结束后,飞行器的方向偏差没有消除,仍旧按照原来有误差的方向飞行,直至飞行器入水[16]。可见开环修偏只需采集一次卫星定位侧偏信息,即可完成修偏过程,但开环修偏控制精度低,且无法消除飞行器射向偏差带来的干扰[17]。采用开环控制侧偏的方式无法在飞行器飞行全程将飞行器精确控制在理论弹道附近[18]。
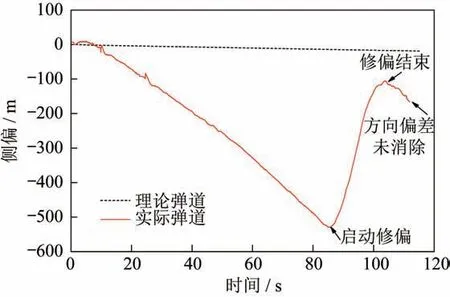
图7 开环修偏的控制效果Fig.7 Control effect of open-loop correction
任务控制器的卫星定位导航控制规律采用了开环与闭环联合控制策略。闭环控制在采样信号稳定的情况下可以有效消除飞行器侧向偏差。某型飞行器采用卫星定位闭环控制时弹道侧向偏差,闭环控制的控制效果比较理想,飞行器一二级分离造成的侧向偏差能够立即消除,如图8 所示。飞行器发射后和机动结束后,弹道能立即向理论弹道靠拢。

图8 闭环导航控制效果Fig.8 Control effect of closed-loop navigation
由于卫星定位存在失捕的可能,利用卫星定位进行闭环导航,当卫星定位失捕时,飞行器弹道控制偏差将难以控制。弹道侧向偏差500 m,飞行后第15 s 卫星定位位置信息闭环参控,第16、25、35 s卫星定位失捕时飞行器的飞行弹道如图9 所示。图中可见,第16、35 s 失捕时弹道偏差为-186.5、373.4 m,侧向偏差无法消除。而第25 s 时失捕造成侧偏为-186.5 s,这种超调在实际供靶中是极为不利的,若超调的方向靠近试验舰艇,则超调越多,对试验舰构成的安全威胁越大[19]。弹道控制偏差与卫星定位失捕时间的关系,在第20、40 s 之后,弹道控制偏差趋向于0,其余时段控制偏差均较大,如图10 所示。图9 和图10 所述情况为假设卫星定位失捕后不再重捕,即失捕时间持续到飞行器入水,若失捕时间较短,闭环控制偏差会减小。
图9 闭环控制在卫星定位失捕时的效果Fig.9 Effect of closed-loop control in the event of satellite positioning loss of capture
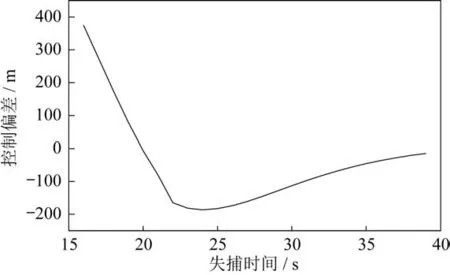
图10 卫星定位失捕时间对控制偏差的影响Fig.10 Effect of satellite positioning lost capture time on control deviation
采用的卫星定位控制规律传递函数框图,如图11 所示[20]。飞行器飞行后T1.5时刻卫星定位参控,T1.5为15 s。若卫星定位正常,控制器发航向控制指令,航向角积分环节断开,卫星定位信息形成的控制信号输出到航向综合放大器与航向角比例环节、微分环节求和。控制器发航向控制指令后,控制器实时判断飞行器的卫星定位侧偏。若卫星定位侧偏大于300 m,控制器采用开环修偏,输出修偏程序,修偏时间为20 s;若卫星定位侧偏小于300 m,且稳定定位大于4 s,控制器采用闭环导航。采用开环与闭环结合的控制方式,可以有效解决卫星定位定位不稳定时对飞行器控制的影响[21]。
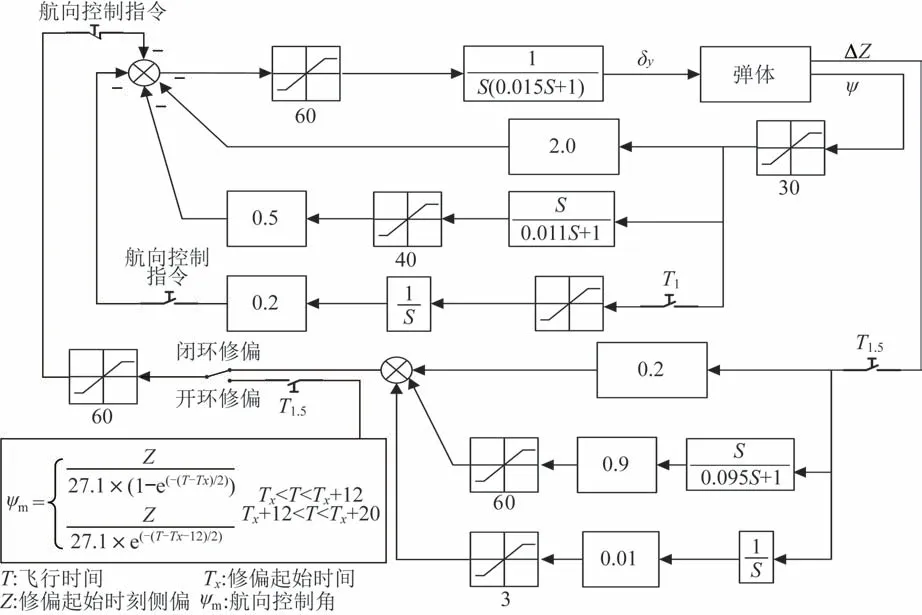
图11 卫星定位控制规律传递函数框Fig.11 Block diagram of the transfer function for the satellite positioning control law
开环控制对卫星定位稳定性要求不高。当侧偏大于300 m 时,采用开环控制。开环控制采用如下修偏程序[22]:
式中:Tx为修偏起始时间;Z为修偏起始时刻侧偏;T为飞行时间;ψm为航向控制角,限幅值为60°。
修偏程序持续时间为20 s,在输出修偏程序期间,卫星是否定位对修偏程序没有影响。修偏程序从第15 s 起控,式(1)在不同侧偏条件下进行开环控制的弹道,如图12 所示。
4 飞行器卫星定位修偏仿真验证及结论
侧偏小于1 500 m 时,开环控制有较好的效果;当侧偏大于1 500 m 时,由于航向控制角ψm达到限幅值,上述修偏程序无法一次完成修偏。修偏结束后,若侧偏大于300 m,则程序会启动第二次开环修偏;若侧偏小于300 m,在卫星定位的情况下,程序会转到闭环导航控制,如图12 所示。按照航向通道控制程序流程对图12 的传递函数进行仿真,如图13所示。侧偏200 m 时,飞行器进行卫星定位闭环导航;侧偏500 m 时,飞行器先进行开环修偏,而后进行闭环导航,从图中弹道可见控制效果良好。
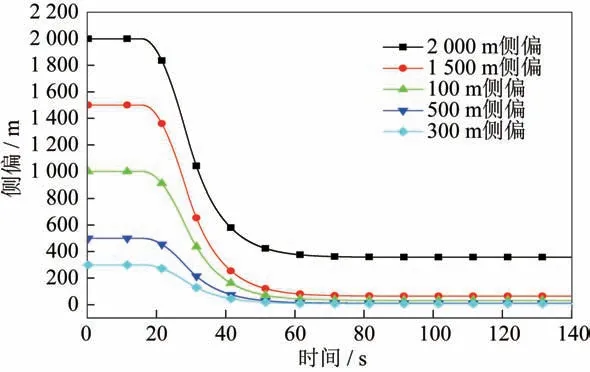
图12 不同侧偏的开环控制弹道Fig.12 Open-loop control trajectories with different lateral deflections

图13 卫星定位修偏、导航控制规律弹道仿真Fig.13 Ballistic simulation diagram under the navigation control law and the satellite-based positioning deflection correction
5 结束语
本文提出将飞行器位置信息闭环到航向控制通路中,形成对飞行器侧向位置的闭环控制,解决了传统飞行控制系统中飞行器航迹容易受到外界因素干扰的问题。飞行器的位置信息可以由卫星定位系统、惯导来提供,同时利用开环和闭环2 种控制律,解决了卫星定位系统数据更新率低、定位不稳定的情况,以及惯性导航长时间工作时定位精度下降的情况,实现了在各种情况下的有效飞行控制,说明本文所提出的控制方法具有良好的效果。
