类比归纳寻本质 通性通法助解题

封海波

教师如何在平时教学中帮助学生开辟思维路径，树立模型意识，掌握解题的通性通法呢？对此，笔者认为，教师关键要精选例题，然后进行适当变式、拓展（一题多变），展示数学问题表象的多样性，凸显问题本质的一致性，让学生领悟数学可以由表及里、由此及彼，发现解题规律，类比归纳通性通法，构建思维路径，从懂得一道题到掌握一类题，这才是基于数学本质问题的解题教学。

下面，笔者以苏科版数学七（上）“数轴上动点问题”为例，谈一谈解决动点问题的相关教学策略。

一、例题呈现

引例 甲、乙两船由相距200千米的两地同时相向驶出，甲船每小时行驶50千米，乙船每小时行驶30千米，请问经过多长时间两船相遇？

这个问题，学生很容易解出。教师可以引导学生把生活中的问题抽象为数轴上的动点问题，通过把引例数值等比缩小，不断变式例题，在动点的变化中，找到不变的数学通法。

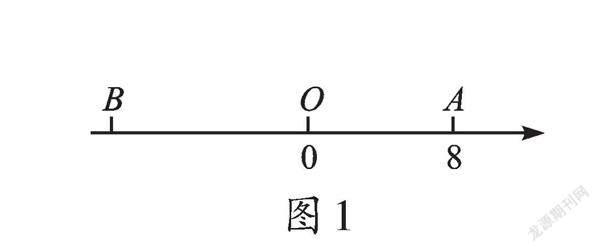
例1 如图1，已知数轴上点A表示的数为8，B在A点左侧，且AB=20。动点P从点A出发，沿数轴向左以每秒5个单位匀速运动，设运动时间为t（t＞0）秒。

学生通过阅读例1，初步得到一些基本信息。在接下来的教学中，教师通过4个问题，从易到难，逐步帮助学生归纳解题思路，类比解题方法，以启发学生思维，引领能力的发展，帮助学生找到适合的解题通性通法，为后期学习打下基础。

二、例题延伸

问题1 现有一动点Q从点B处向右匀速运动，速度是每秒3个单位长度，若点P、Q同时出发，P、Q经过多长时间相遇？

生1：我可以直接列出算式20÷（5+3）=2.5（秒）。

生2：我们还可以利用方程解决。设相遇时间为t秒，可列方程5t+3t=20，解得t=2.5。

生3：我们还可以用数轴上的点对应的坐标来表示。其中，P点可表示为8-5t；Q点可表示为-12+3t。在数轴上，两个点相遇，表示两个点在同一位置，那么它们的坐标就相同。因此，我们可列方程为-12+3t=8-5t，解得t=2.5。

［设计意图］教师引导学生从不同的角度，用不同的方法去解决问题，激发学生思维。

问题2 与问题1条件相同，若点P、Q同时出发，问点P运动多少秒时与点Q相距为2？

师：问题2有几种可能？

生5：有两种可能。一种是P、Q还没相遇时，两点相距为2；一种是P、Q两点相遇后，两点相距为2。

师：请你用坐标轴上的点来表示。

生6：P点可表示为8-5t；Q点可表示为-12+3t。当P、Q还没相遇时相距2，可列方程为8-5t-（-12+3t）=2，解得t=[9/4]；同理，当P、Q相遇后相距2，解得t=[1/14]。

［设计意图］通过类比，教师引导学生把动点运动后的位置用数轴上的点的坐标表示出来，然后把问题转化为坐标之间的距离来解决，让学生体会坐标化的优势。

问题3 动点Q从点B出发，沿数轴向左匀速运动，速度为每秒3个单位长度，若点P、Q同时出发，问点P运动多少秒时追上点Q？

生7：我可以直接列出算式：20÷（5-3）=10（秒）。

生8：可以列方程解决。设相遇时间为t，列方程为5t-3t=20，解得t=10。

生9：在坐标轴中，P点可表示为-12-3t；Q点可表示为8-5t。P追上Q，即两点坐标相同，可列方程为-12-3t=8-5t，解得t=10。

［设计意图］把相遇问题改为追击问题，继续让学生进行类比，体会三种解题方式的优劣性，强化学生的认知。

问题4 若AP的中点为点M，PB的中点为点N。点P在运动的过程中，线段MN的长度是否发生变化？并说明理由。

生10：此题依然有两种情况，一种是点P在AB中间，一种是P点在B点的左侧。解题思路如下……

［设计意图］教师借助数轴把实际问题转化为数学模型，利用这种模型思想研究问题，可以使问题化难为易，化繁为简。反过来，当面对实际问题时，我们同样可以通过建立数轴模型来解决。

三、教学反思

动点问题静点化是本节课的主要思路。第一步，熟读题目，画出图形；第二步，表示各點的坐标，厘清动点的速度、时间、路程；第三步，动点在数轴上所表示的数用字母表示；第四步，借助数轴上线段长度、线段中点的代数表示方法，根据题目列出方程，并解方程。这样就归纳出数轴上的动点问题的“通性通法”，从而帮助学生化难为易，化动为静，分类讨论，抓住动点，代数表示，以不变应万变，寻找破题点。

数轴上的动点问题是七年级一个难点，很多学生畏惧。在小学四年级时，学生开始学习相遇问题和追击问题，教师通过引导学生画线段图，利用数形结合思想归纳出相遇问题的数量关系式；到了五年级，学生开始学习方程，教师引导学生利用数形结合，找到等量关系，再利用方程解决常见的相遇问题、追击问题等，学生思维又一次飞跃；进入初中后，教师将小学方程问题中的两个形象人物“小明与小红”抽象为“A点与B点”，再逐步引导学生认识、理解并解决动点问题。可见，数轴是学生进入初中后有力的数形结合工具。

教师平时要多做题，整理和归纳同类型题，通过专题课型或者一题一课的形式，在课堂上循序渐进，引导学生用数学的眼光看待问题，用数学的语言构建模型，力求将解题后的反思归纳形成解题经验，构成一个系统，一套思维路径，以形成解决一类问题的通法。

（作者单位：江苏省南京市中华中学上新河初级中学）